BP神經網絡在步進電機細分控制的應用
肖 鋒
(佛山供電局,廣東 佛山 528000)
步進電機的細分控制,不僅能改善電機低速運行時的性能,而且可以提高電機的控制分辨率。目前常用的細分控制法參見文獻[1-3],主要有插值法、近似波形法、曲線擬合法、矢量控制法。這些方法都是以一定的數學模型為基礎,且都是在某些理想的條件下提出,如磁路線性化、轉矩特性理想化、忽略高次諧波等。本文利用 BP神經網絡不需要具體數學模型就能夠以任意精度逼近任意復雜的非線性映射的特點,引入到步進電機細分控制中,實現步距角均勻控制。
1 步進電機細分控制原理
細分控制就是將步進電機繞組原來整步運行的步距角細分成若干個較小的步距角,解決低速運行時出現低頻振蕩、失步,高頻帶負載能力下降的問題,同時提高電機的控制精度[5]。如圖 1所示,步進電機細分前步距角為θ=π/2通過改變 A、B相繞組電流,轉子在兩繞組產生的合成力矩作用下步距角由原來θ=π/2變為θ/3。

圖1 步進電機細分后運行圖
2 細分控制的實現
本文以德 TI公司型號為 TMS320LF2407A的DSP為控制核心,ST公司生產型號為L298N的驅動芯片構建控制步進電機定子繞組電流,實現步距角細分。檢測信號為步進電機步距角,并通過顯示平臺顯示。細分控制實驗平臺示意圖如圖2所示。

圖2 細分控制實驗平臺
細分控制電流是通過PWM(脈沖脈寬調制)技術實現的。本文的控制對象為兩相永磁步進電機,利用TMS320LF2407A兩個獨立比較單元產生4路PWM波控制L298N驅動輸出所需的細分控制電流,實現對步距角的控制。在這個過程中有兩個非線性的過程:①PWM控制信號經過驅動控制輸出電壓;②輸出電壓通入步進電機定子繞組后輸出的步距角,控制框圖如圖3所示。

圖3 控制信號到步距角的控制框圖
由于驅動與步進電機無法建立精確的數學模型,因此很難實現對電機的精確控制。本文將驅動、繞組電流、步進電機看成一個非線性過程,利用BP神經網絡具有逼近任意非線性函數的能力計算得到這個過程的相應控制信號。給定步距角為神經網絡輸入,輸出為控制信號(占空比)。將控制信號(占空比)輸入到DSP中就可以得到所需要的步距角,這樣利用占空比這個精確的控制量就可以實現對步距角的控制,不需要通過測量繞組電流值,這樣可以避免電流測量產生的誤差,提高控制精度,簡化控制過程。
本文神經網絡的訓練是通過 Matlab平臺實現的。Matlab神經網絡工具箱為開發者提供很多基于神經網絡理論為基礎的典型框架和相關函數。這些框架和函數減少了許多手動計算的工作,不僅提高了效率而且還提高了計算的準確度和精度。BP神經網絡的建立的基本步驟如下所示。
1)數據歸一化,將輸入和輸出的數據進行歸一化處理,加快網絡訓練的收斂性。首先輸入一組歸一化后的占空比值M= [0 7 8 22 65 143 171 194 207 230 285 306 324 391 404 500;500 404 391 324 230 143 116 94 83 65 35 27 22 8 7 0]/500,然后,用光電編碼器測出這組控制占空比值所對應步進電機的步距角(角位移),測出的角位移數據為數組N=[0 4 5 9 14 17 17 18 18 19 20 20 20 22 22 25]/25。
2)用newff函數創建一個BP神經網絡。輸入函數net=newff(N,M, [3, 3]);建立一個BP神經網絡函數。其中隱含層的傳遞函數為tansig(正切函數),輸出層傳遞函數為purelin(線性函數),學習函數為learngdm(帶動量的梯度下降法的BP學習規則)。訓練函數為trainlm(Levenberg_Marquardt的BP算法訓練函數)。
3)用train函數訓練BP神經網絡。設置訓練步數。net.trainParam.epochs=1000;訓練目標誤差net.trainParam.goal=0;學習率 net.trainParam.lr=0.02。設置完成后,輸入命令net=train(net,T,P) 對BP網絡進行訓練。
4)神經網絡訓練好后,需要拿測試樣本進行測試,用來檢驗網絡訓練是否達到所需要的效果。在數據采集的過程中,還采集了一組數據用來測試訓練結果。這組數據的輸入為步進電機步距角位移數組N1=[0 5 10 15 20 25]。用sim函數進行仿真,輸入命令M1=sim(net,N1) 后得到結果為[0 8 26 92 289 500;500 387 312 197 36 -1] /500,理想輸出的占空比值為 [0 8 27 83 285 500; 500 391 306 207 35 0]/500。經過比較,用BP神經網絡模擬出來的占空比值是非常理想的,可以很好的滿足要求。為了更直觀的觀察神經網絡的訓練情況,輸入命令plot(N,M2,N,M2, '+',N1,M1, '*') 后可以得到數據的擬合曲線,如圖4所示。

圖4 訓練擬合曲線圖
3 實驗及結果分析
為驗證BP神經網絡在步進電機細分控制中的效果。對步進電機做了3細分、8細分2組實驗。其中步進電機3細分和8細分電流波形如圖5、圖6所示,對應細分角位移數據表1、表2所示。
對實驗數據進行分析表明,運用 BP神經網絡算法能夠實現對步進電機的均勻細分控制。從定子繞組電流波形可以看出,要使步距角均勻細分,定子繞組的電流波形并不是規則的正弦波,會有一定的變形,這也進一步說明了步進電機的輸入繞組的電流與輸出角位移之間的關系的非線性和復雜性特點。

圖5 步進電機3細分繞組電流波形
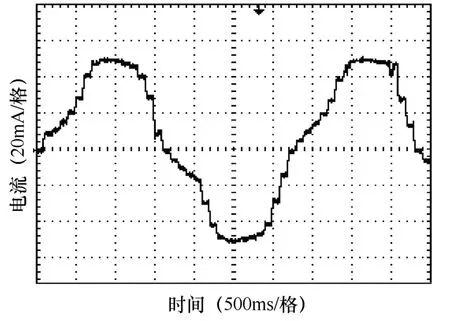
圖6 步進電機8細分繞組電流波形
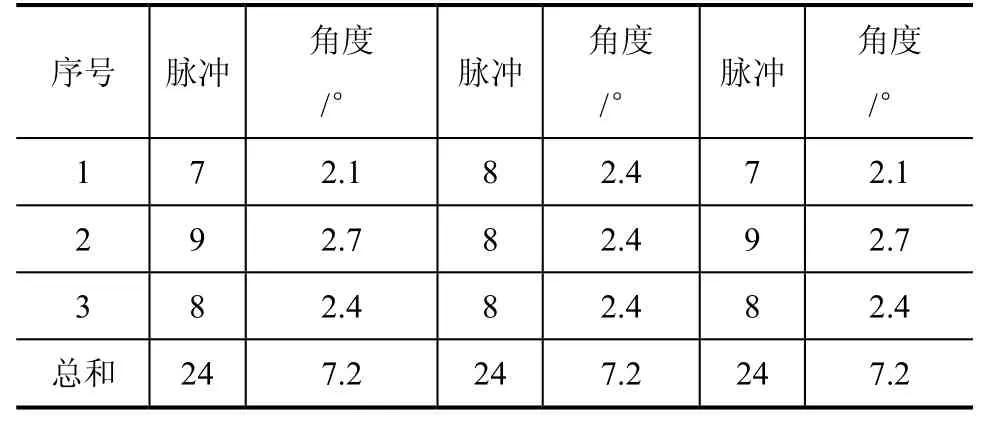
表1 步進電機3細分角位移數據表

表2 步進電機8細分角位移數據表
4 結論
本文引入 BP算法,在不需要建立精確的數學模型的情況下實現步進電機步距角均勻細分控制。相比過去通過采用近似數學模型的控制方法得到了很大的簡化。同時采用“控制電流占空比—輸出步距角”特殊的訓練方式,利用占空比這個精確的控制信號代替需要測量的電流值控制信號,提高控制精度。
[1] 馬西庚, 張衛東. 步進電機細分控制輸入輸出特性的研究[J]. 石油大學學報(自然科學版), 1998, 22(3):98-100, 11.
[2] 孫宏剛. 兩相混合式步進電機細分驅動控制器的研究[D]. 武漢: 華中科技大學, 2006: 19-24.
[3] 孫勝利. 步進電機細分驅動獲得均勻步距的方法研究[J]. 微特電機, 1998(5): 21-23, 26.
[4] 劉闖. 一種基于電壓 SVPWM 的三相步進電機細分驅動技術研究[J]. 微電機, 2008, 41(3): 45-47.
[5] 阮建國. 步進電機可變細分微機控制系統[J]. 微電機, 1987(2): 25-27.

