考慮高階振型阻尼比的結構響應研究

梁曉東 李雙龍 汪忠明 王傳甲

(1.奧意建筑工程設計有限公司，廣東 深圳 518031;2.合肥工業大學土木與水利工程學院，安徽 合肥 230009)

0 引言

阻尼是用來描述結構在振動過程中能量耗散特征的參數，是影響結構動力反應的重要因素之一。在地震反應時程中，有足夠的阻尼存在，結構就能吸收較多的地震動能量，可以有效地減小振幅和應力，改善結構的振動狀況。基于對阻尼的認識，國內外學者們提出了不同的阻尼模型［1-5］，并對阻尼模型進行了一些分析研究與擴展［6，7］。這類阻尼模型基本上可以分為兩類，一類基于阻尼的物理過程描述，每種假設對應著一種具體的阻尼現象;一類著重數學處理上的方便，并不跟某種具體的阻尼物理過程相對應。鑒于結構在地震反應分析中阻尼機理的復雜性，沒有哪種阻尼理論能涵蓋和解釋結構動力分析中阻尼耗能的所有物理過程。人們對結構地震反應分析主要是為了獲知結構反應量，因此在工程分析中常選取數學處理上比較方便的阻尼模型，根據與結構反應物理量等效的原則來確定阻尼參數。

在建筑結構的動力分析中，出于使用方便，人們常使用正交阻尼，而非正交阻尼因為計算較為麻煩用得較少。最一般的正交阻尼矩陣是Caughey 阻尼矩陣［4］，Caughey 阻尼在滿足與振型正交的同時，可以指定系統的j 個(j=1～n)振型的阻尼比，其中n 為體系的自由度。當r=2，即指定兩個振型的阻尼比時，就是Rayleigh 阻尼。盡管Caughey 經典阻尼矩陣使得指定任意階振型的阻尼系數成為可能，但是Caughey 阻尼在數值上是具有病態條件的，因為系數可能會相差幾個數量級，而且，如果在Caughey級數中包含兩項以上時，盡管k 是帶狀矩陣，對于集中質量體系，m是對角矩陣，但c 將是滿陣，這樣會極大地增加大型體系分析的計算代價。而Rayleigh 阻尼模型雖然實施起來方便，但是本身也有很多缺陷:首先，從物理上講，剛度比例阻尼部分βK 從直覺上很容易接受，因為它可以用來模擬層間變形所產生的能量耗散，但是質量比例阻尼αM 則很難理解，因為用它來模擬的空氣阻尼在大多數結構中很小，可以忽略不計。

其次，在考慮的結構反應中，一般取較低的兩階頻率和阻尼比來確定阻尼常數α 和β，用這種方法確定的阻尼常數，只能保證兩個振型的阻尼比為一個指定經驗值，難以保證其他振型的阻尼比也為同一個值。當用以上方法得出的計算阻尼比小于指定值時，則計算結果對振型阻尼估計不足，計算效應偏大，可能導致設計偏保守;相反，當用此法得出的計算阻尼比大于指定值時，則計算結果對振型阻尼估計過大，計算效應偏小，可能導致設計偏不安全。

最后，在通常的大型動力時程計算中，由于剛度退化引起的數值不收斂，因此常采用僅設α 系數的策略來算Rayleigh 阻尼，這樣實際上不僅物理上解釋不通，而且得出來的值，會使設計偏保守，提高成本。

目前，公認可靠的結論是上部結構體系具有在相當寬的頻率范圍內模態阻尼比不變的特性，而且偏于保守的，結構的下部阻尼不予考慮，我國規范規定，一般混凝土結構為0.05。

隨著基于性能的抗震設計方法的提出，對結構在罕遇地震作用下的彈塑性時程分析的清楚把握必不可少，而ABAQUS 以其強健的非線性計算能力、廣泛的模擬性能和多種靈活的接口，在科學研究和工程領域得到了廣泛的開發應用。

本文通過振型向量構造適當的阻尼矩陣，使結構多階振型的阻尼比可以為指定值，對ABAQUS 進行二次開發，利用編制的子程序將等效阻尼力正確地施加在結構上，并計算比較了一工程結構考慮多階振型阻尼比的層間位移角和基底剪力結果。

1 阻尼矩陣構造

當包括阻尼時，結構的動力學方程［8］為:

式中:u——節點位移矢量;

m——質量矩陣;

c——阻尼矩陣;

k——剛度矩陣;

p(t)——隨時間變化的外力矢量函數。

將節點位移矢量u 以固有振型為基展開:

式中:qr——振型坐標;

φr——第r 階振型矢量;

Φ——N×N 階振型矩陣。

將式(2)代入式(1)，并且前乘ΦT，得到:

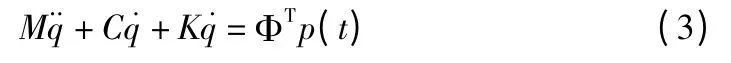
其中，M=ΦTmΦ;C=ΦTcΦ;K=ΦTkΦ，固有振型的正交性意味著M，K 是對角陣，如果要使式(3)解耦，則C 必須也是對角陣，即:

其中，diag()為對角陣函數。

式(3)的分量形式為:

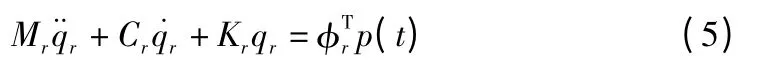
式(5)變形為:

其中，ξr為第r 階振型的阻尼比，ξr=cr/2ωrMr。

利用M=ΦTmΦ，式(4)變為:

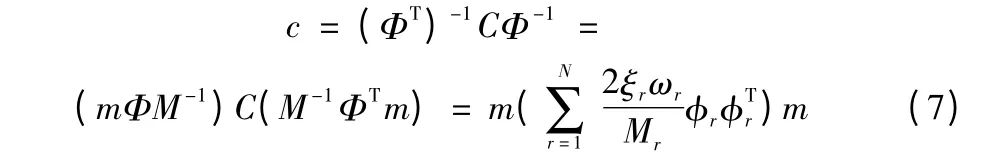
這樣構造出的阻尼矩陣c［8］不僅使得式(3)能解耦為分量形式的式(5)，而且能夠使相當寬的頻率范圍內結構的振型阻尼比為指定值，考慮到計算效率，式(6)中只包括前J 個振型是合理的，因為這些振型對于反應的貢獻是主要的。因此，式(7)改寫為:

根據以上公式編制程序實現阻尼矩陣的多階振型表達。

2 工程算例分析和ABAQUS 二次開發實現

2.1 工程概況

合肥置地廣場·A 座項目位于安徽省合肥市城市新中心——政務文化新區，北依龍圖路，東臨星光西路，西靠懷寧路。項目用地北面為省廣電中心，東面為城市綠軸景觀帶，西面為省文博園。項目總占地面積51 188 m2，總建筑面積達到380 000 m2，結構三維模型如圖1 所示。

圖1 三維結構模型圖

本工程地上47 層，地下4 層，主要屋面標高為197.60 m，采用鋼筋混凝土框架—核心筒結構體系。計算嵌固端取為地下室頂板面，一層樓面在主塔樓周邊設置抗震縫。為減小柱截面，在結構的中下部采用型鋼混凝土柱，上部采用普通混凝土柱。框架梁采用鋼筋混凝土梁。

2.2 計算模型與相關參數選取

本場地特征周期為0.37 s，彈性動力時程分析時，時長為40 s，步長為0.01 s，地震加速度最大值為344.49 cm/s2。

取地下室頂板以上結構為彈性動力時程分析對象，地震波從地下室2 層頂板處的豎向構件端點輸入，結構分析模型由彈性梁單元與彈性殼單元構成。梁與柱采用可考慮線性剪切變形效應的Timoshenko 梁單元B31，墻、樓板及連梁采用4 節點縮減積分殼單元S4R 和S3。

2.3 ABAQUS 二次開發

本文基于大型通用有限元軟件ABAQUS/Explicit 求解器［9］，開發VDLOAD 子程序將構造的阻尼矩陣通過阻尼力的形式施加在工程結構上，代替了原有的低階阻尼模塊，對一工程結構在振型累積質量參與系數超過90% 的階數下，進行彈性動力時程分析。

在ABAQUS 中，VDLOAD 子程序被用來給一個或多個點集定義隨位置、時間、速度等變化的分布力，這些點出現在基于單元或表面的非均勻載荷定義里，VDLOAD 子程序在積分點處被調用。VDLOAD 子程序里的變量說明如下:

value:分布力的大小;nblock:調用點的數目;ndim:坐標方向數目。

steptime:時間步長;totaltime:總時間;curCoords:調用點的當前坐標。

amplitude:引用荷載幅值的當前值;velocity:調用點的當前速度。

dirCos:壓力類型荷載下，表面、邊、管或梁的方向余弦。

jltype:分布力類型標識符。

通過VDLOAD 將阻尼矩陣變為阻尼力施加于結構，并指定各階振型下阻尼比都為0.05。

2.4 層間位移角和基底剪力分析結果比較

將構造的阻尼矩陣退化為只使用一階振型向量來考慮阻尼，用本文開發的子程序與ABAQUS 自帶的α 阻尼下的層間位移角和基底剪力進行了比較，結果如圖2 和圖3 所示，吻合程度很高，驗證了構造的阻尼矩陣的合理性。當僅考慮一階振型α 阻尼比時，本文比較了指定多階振型阻尼比情況下的層間位移角和基底剪力，進而使用此程序計算多階振型下的響應，由圖4 和圖5 可以看出，考慮不同階振型下的結構層間位移角，隨著計入振型數的增多，層間位移角逐漸變小，類似地，基底剪力隨著振型數的增多，剪力幅值也逐漸減小，說明考慮的振型數越多，阻尼消耗的能量越多，同時當振型數取到一定值時，后面的貢獻變得很小。這樣對于超高層結構，比只考慮兩階振型的Rayleigh 阻尼或僅考慮一階振型的α 阻尼更能準確地反映真實結構的耗能及基底剪力態勢，為結構設計提供指導。

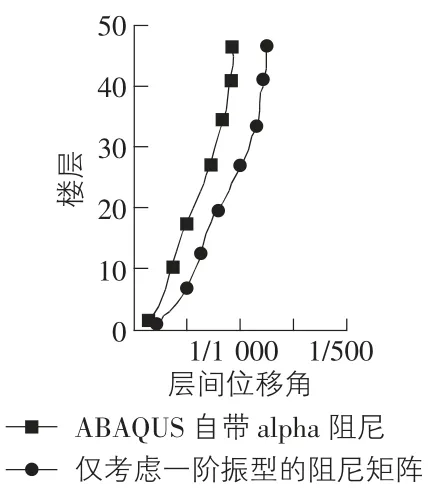
圖2 層間位移角結果比較

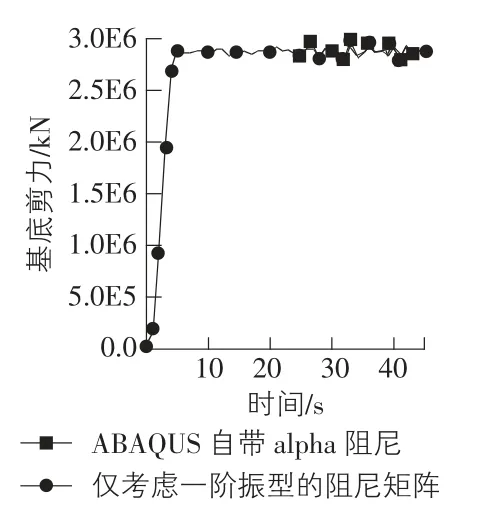
圖3 基底剪力結果比較

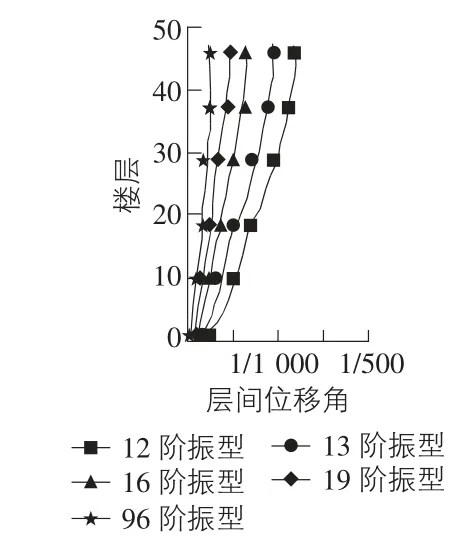
圖4 Y 向層間位移角比較

圖5 Y 向基底剪力比較

3 結語

通過基于ABAQUS 二次開發平臺施加的多階振型阻尼力的動力時程分析計算，可以得出:高振型阻尼比主要影響結構的層間位移角和基底剪力，特別是結構的中上部的層間位移角，若采用不計高振型阻尼比影響的Rayleigh 阻尼，結構在地震作用下的層間位移角偏大，不能反映結構真實高階振型的影響，基于此分析結果的設計控制會相對偏于保守，而通過施加高階振型阻尼比的分析，更加能客觀地反映超高層結構的高階響應，基于此設計控制能合理地降低成本，為設計提供理論依據。

［1］Bert，C W.Material Damping:An Introductory Review of Mathematical Models，Measures and Experimental Techniques［J］.Journal of Sound and Vibration，1973，29(2):129-153.

［2］Leger P，Dussault S.Seismic-Energy Dissipation in MDOF Structures［J］.Journal of Structural Engineering，1992，118(5):1251-1269.

［3］Hart，G C，Vasudevan R.Earthquake Design of Buildings:Damping［J］.Journal of the Structural Division，ASCE，1975，101(1):11-30.

［4］Clough R W，Penzien J.Dynamics of Structures ［M］.New York:McGraw-Hill，1975.

［5］Liang Z，Lee G C.Representation of Damping Matrix ［J］.Journal of Engineering Mechanics，ASCE，1991，117(5):1005-1019.

［6］黃宗明，白紹良，賴 明.結構地震反應時程分析中的阻尼問題評述［J］.地震工程與工程振動，1996，16(2):95-104.

［7］董 軍，鄧洪洲，王肇民.結構動力分析阻尼模型研究［J］.世界地震工程，2000，16(4):63-69.

［8］A K Chopra.結構動力學:理論及其在地震工程中的應用［M］.第2 版.謝禮立，呂大剛，譯.北京:高等教育出版社，2007.

［9］ABAQUS Inc.ABAQUS User's Manual，V6-9，2009.