多級聯調機構的六西格瑪設計及響應面法優化

趙 雷，采 峰，馬 召

（1.中航工業沈陽發動機設計研究所，沈陽110015；2.中航工業發展研究中心，北京100029）

0 引言

燃氣輪機上多級聯調機構用于連接多級靜子，并同時驅動多級聯動環，使各級靜子葉片的角度在風扇或壓氣機一定轉速范圍內按照一定規律變化。其設計難點在于各級靜子葉片角度隨轉速的匹配關系。傳統的連桿機構設計有解析法、作圖法、實驗法，但是普遍存在工作繁瑣、效率低下、誤差較大的問題，設計輸入即規律變化時需全盤推倒重做。解析法雖然精確度較高，但構建位置方程相當復雜，計算求解也比較麻煩，難以推及一般可調機構工程設計應用[1-2]。

六西格瑪設計(DFSS)是以數理統計為基礎，從獲得數據、處理數據和分析數據方面綜合運用多種定性或定量的統計工具得出結果或趨勢推論的綜合性設計理念。完整的DFSS流程包括定義、測量、分析、設計、驗證幾個階段。DFSS運用CDM和RDM工具分析客戶需求，用SIPOC工具統計輸入和輸出變量并進行重要度分析，運用多層QFD質量工具識別關鍵節點和客戶需求的耦合關系，并進行FMEA失效模式及風險分析，為后續全因子試驗設計DOE提供基礎。通過回歸方程和假設檢驗可以建立定量的轉換函數供最后的優化設計使用[3-4]。

本文探討了1種基于六西格瑪數據分析的操縱機構設計方法，通過對機構輸入和輸出數據的試驗設計（DOE）和采集，運用科學嚴謹的數理統計工具，對影響輸出的有效輸入參數項進行了定量篩選和統計檢驗，建立了輸入和輸出參數間的響應模型，并對輸出參數做了望目優化，分析過程和結果均有統計數據支持，具有求解快速、便于誤差分析、對調節規律的更改反應快速的特點。

DFSS設計流程最后還包含驗證階段、制定測試計劃、開展驗證研究，以確定最終的設計結果，為突出重點，本文忽略了驗證階段研究的描述[5]。

1 聯調機構的問題域分析

聯調機構作為4連桿多體運動機構，實質是函數再現求解問題。多體運動機構一方面是已知各連桿參數，求解輸出端的運動規律，另一方面是反問題，即已知運動輸出端運動規律，求解滿足條件的各連桿參數。2個問題皆可用1個方程來表示

式中：Y 是輸出；x 是連桿參數。

無論是已知x 求y 的方程求解，還是已知y 求x的優化問題，都需要首先建立這個函數關系式。

聯調機構的連桿參數和輸出端規律響應，可以認為是多元線性回歸模型

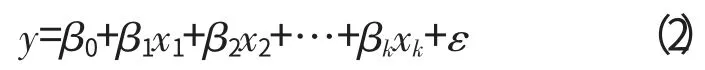
式中：βk為未知回歸系數。

聯調機構的求解即歸結為對回歸系數的求值，其數學上的工作為：求解回歸方程；對式（2）的假設檢驗，確定模型的有效性；方差分析(ANOVA)，表明至少有1個變量對響應的貢獻是顯著的。

確立了回歸方程且通過了假設檢驗，可以運用此方程對聯調機構正反問題進行求解。

2 全因子2水平試驗設計選擇因子

DOE可用于系統地調查影響產品質量的過程變量或產品變量。確定影響產品質量的過程條件和產品組件后，可以有針對性地進行改進，以增強產品的可制造性、可靠性、質量和現場性能。

由于資源有限，從執行的每個試驗中獲取最多信息是非常重要的。與未經計劃的試驗相比，設計完善的試驗可以產生更多信息，而且通常需要較少的游程。此外，設計完善的試驗還將確保可以評估已確定為重要因素的效應。例如，如果相信2個輸入變量之間存在交互作用，則確保在設計中包括這2個變量，而不是進行“1 次1個因子”試驗。當1個輸入變量的效應受另1個輸入變量的水平影響時，就會出現交互作用。

本項目中，通過QFD等質量工具初步挑選了4個機構參數用于試驗設計的因子分析[8-9]，分別為調節臂長度、角度、拉桿座半徑、角度。該方法便于先期過濾因子，減少數據收集量和DOE分析計算的步驟。進行DOE的目的，是分析這4個參數各自及交互高次項對響應的影響。采用4因子2水平的全因子試驗設計，包含中心點以考察彎曲效應。這樣將共有24+1=17次試驗項。

響應值的數據收集可通過加工試驗件實物裝配打壓獲得，但需加工16套不同規格的連桿和調節臂，加工和裝配工作量巨大、成本很高。本項目采用UG運動學模塊建立機構運動仿真模型，分析機構內各零件的運動副關系，設置運動初始態和邊界條件，記錄運動全過程位置數據，求得每個試驗項的響應值并填入正交表中供后續分析使用[6-9]。

3 分析因子設計

采用Minitab軟件進行分析，分析結果及殘差如圖1所示，效應分析見表1。從表中可見，P值是否小于0.05可判定該因子效應是否顯著，即對響應影響較大，是必須要考察的因子。由圖1可分析此次分析的可信度。

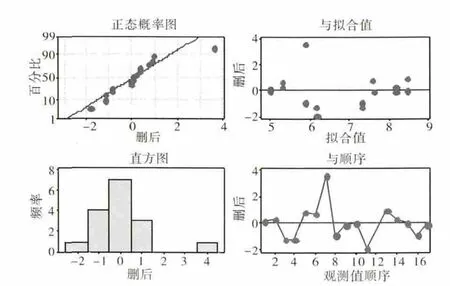
圖1 殘差

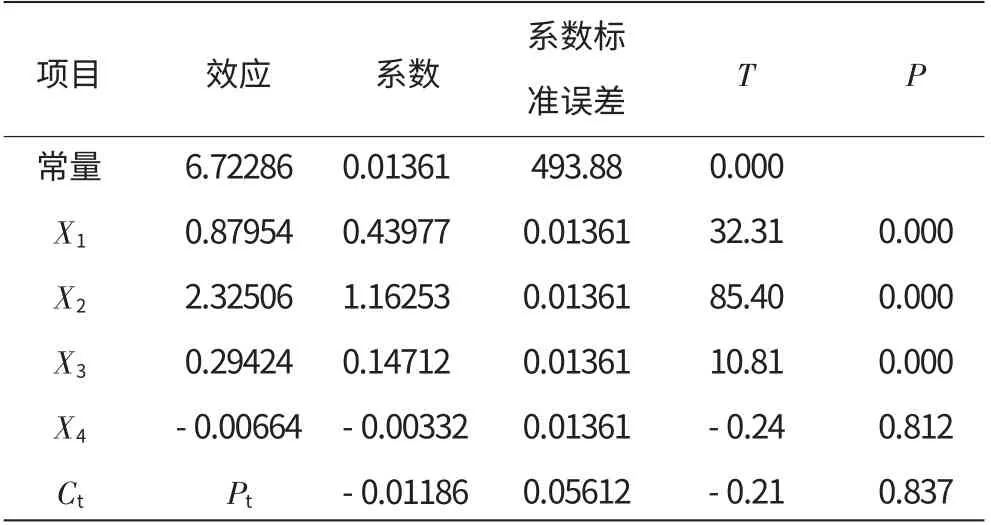
表1 DOE效應分析

從圖中可見，殘差分布符合正態分布，隨機無規律，殘差和為零。

響應方差分析見表2。

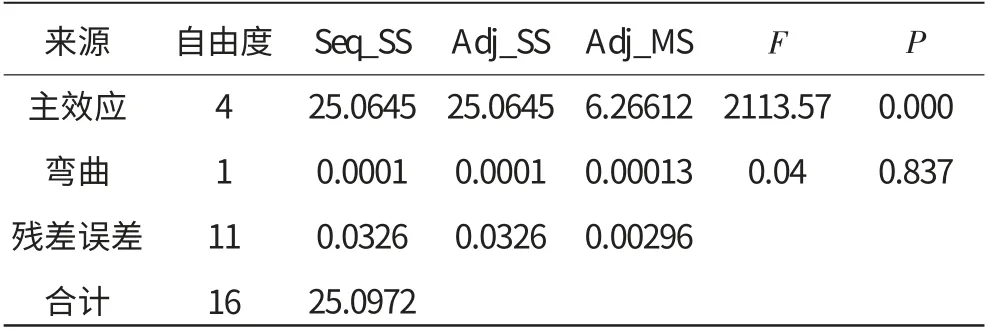
表2 DOE方差分析

從表中得出如下結論：

（1）主效應P值小于0.05，說明至少有1個因子顯著；

（2）常量、X1、X2、X3的P值小于0.05，是顯著項；

（3）彎曲P值過大，說明彎曲效應不顯著。

由此說明此次分析各因子階次及交互作用合理可用，效應顯著，即式（2）成立。

4 響應面模型分析及優化

響應曲面法（RMS-ResponseSurfaceMethodology）是結合了數學方法和統計方法，以試驗設計為基礎的用于多變量問題建模和分析的1種統計處理技術。

當確認了少數重要因子后，采用響應曲面模型來建立響應方程，并尋找可以產生最佳響應的因子設置。可按如下步驟進行：

（1）給出因子2水平值，生成正交表；

（2）求得每項運行的響應值，完成正交表；

（3）按因子2次項、交互項、1次項進行響應面分析；

（4）根據分析結果和殘差圖進行判定，分析結果見表3。

響應方差分析見表4。

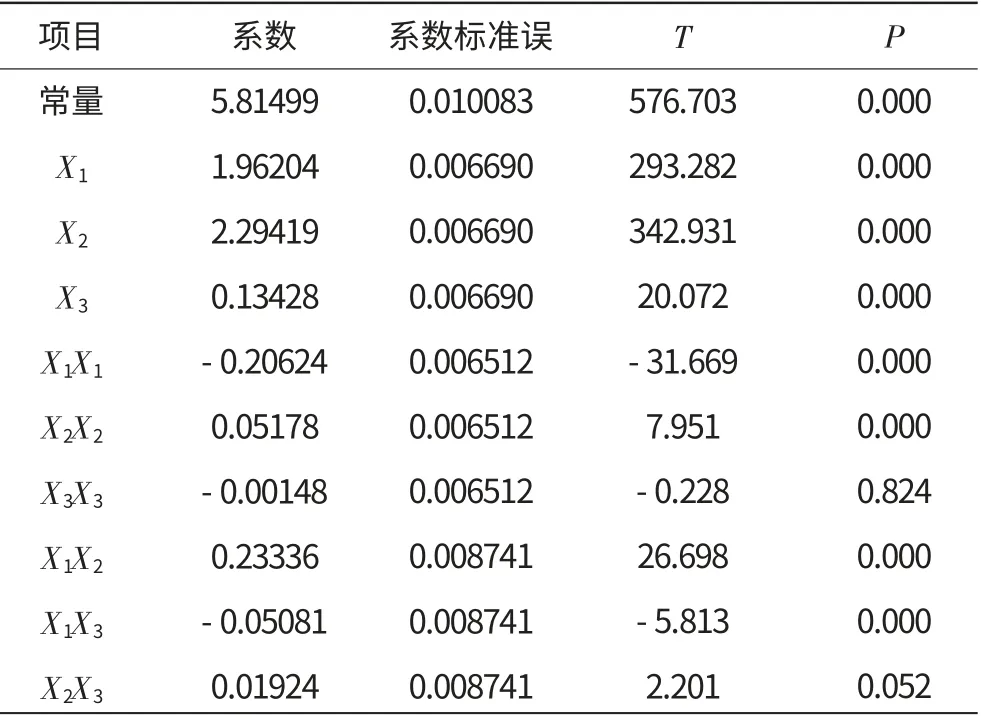
表3 RSM效應分析

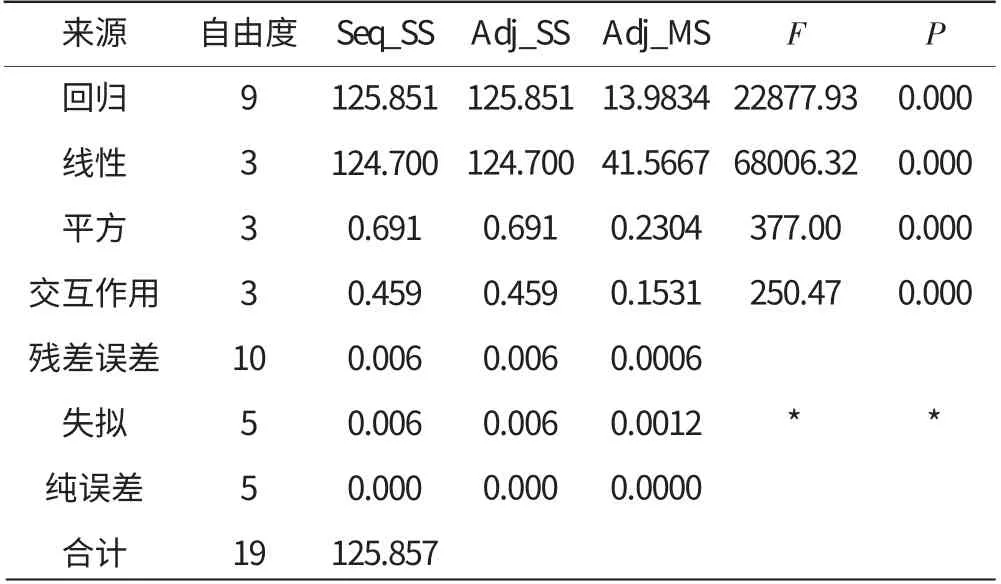
表4 方差分析

由表3、4中的方差分析結果可得：

（1）回歸有效，線性和2次項、交互作用同樣顯著；

（2）常量、X1、X2、X3和除X3的2次項外所有2次項均顯著。

響應面模型如圖2所示。圖中是保持X3的水平，及X1、X2因子對響應的綜合效應，在因子取值區間內對響應Y 的分布形成1個曲面。從圖中可見使Y 取值最小的X1、X2的范圍。這也是后文優化的基礎[10-12]。

分析所得去量綱化系數即為式（2）中的回歸系數，從而建立此響應面數學模型。

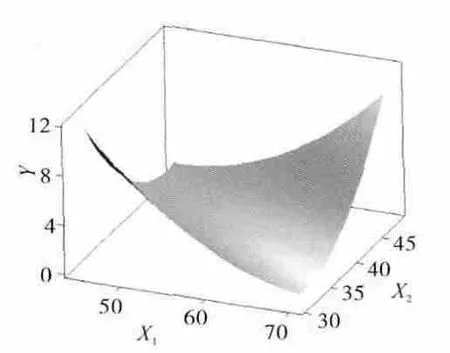
圖2 響應面模型

5 蒙特卡羅法公差分配設計

以上對聯調機構的設計，通過對試驗數據的分析，識別了關鍵因子，建立了數學模型，并用優化的方法確定了各因子的取值。為進一步降低機構的制造成本，提高質量，有必要根據響應公差對各因子的制造容差進行分配，在此采用蒙特卡羅法進行公差分析，模擬各因子在不同公差容限配對條件下的響應，避免等公差設計或經驗設計的不足。

蒙特卡羅法是1種模擬抽樣仿真算法，可以對任意分布進行模擬。機械零件的制造誤差隨機分布，可認為符合正態分布，機械零件的公差可用±3σ 表示。為滿足一定的計算精度，模擬可增加計算次數[13-15]。蒙特卡羅模擬結果如圖3所示。

從圖中可見，各因子的公差對響應的敏感度不同，在設計中可以對敏感度較高的因子給予較嚴格的公差，對敏感度低的因子給予相對寬松的公差，這樣在制造上節約了成本。

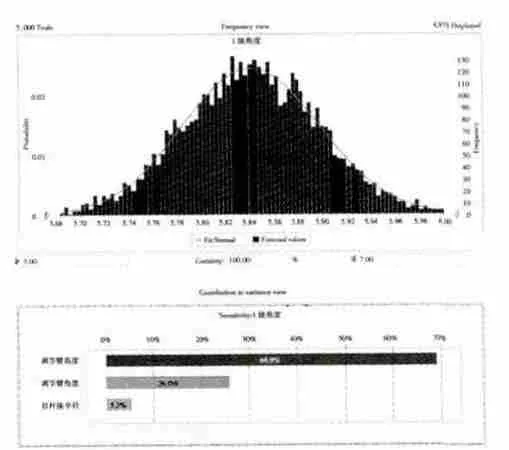
圖3 蒙特卡羅模擬結果

6 結束語

通過六西格瑪設計理念，將數理統計理論與相關工具結合起來，規范了設計過程，為設計決策提供堅實的數據支持。項目實踐證明，六西格瑪設計方法科學、有效，不僅可滿足設計任務，還可以完成設計方法的梳理，可用于設計模型的建立，在工程實踐中具有一定實用價值。

[1]孫恒，陳作模，葛文杰.機械原理（7版）[M].北京：高等教育出版社，2006：109-139．SUN Heng，CHEN Zuomo，GE Wenjie.Theory of machines and mechanisms(seventh edition)[M].Beijing：Higher Education Press，2006：109-139.（in Chinese）

[2]楊勇剛，張力.幾種搖臂與聯動環連接結構對比分析[J].航空發動機，2012，38（6）：34-37．YANG Yonggang，ZHANG Li.Contrast analysis of several rocker and drive ring connecting structure[J].Aeroengine，2012，38（6）：34-37.（in Chinese）

[3]鄒峰，汪邦軍，郝建春.航空工業六西格瑪設計流程模式研究[J].航空標準化與質量，2009（1）：25-27.ZOU Feng，WANG Bangjun，HAO Jianchun.Aeronautic industry Six Sigma Design pattern research[J].Aeronautic Standardization and Quality，2009（1）：25-27.（in Chinese）

[4]何楨，梁昭磊，鄒峰.六西格瑪設計模式及其應用[J].工程機械，2006（7）：62-64.HE Zhen，LIANG Zhaolei，ZHOU Feng.Six Sigma Design pattern and application construction machinery and equipment[J].Engineering Machinery，2006（7）：62-64.（in Chinese）

[5]段愛琴，王興華.應用六西格瑪設計究竟改變了什么?[N].中國航空報，2011-04-12（12）.DUAN Aiqin，WANG Xinghua.What did DFSS changed us？[N].China Aviation News，2011-04-12（12）.(in Chinese)

[6]胡小康.UG NX4運動分析培訓教程[M].北京：清華大學出版社，2006：136-147．HU Xiaokang.UG NX4 kinematics simulation training guide[M].Beijing：Tsinghua University Press，2006：136-147.（in Chinese）

[7]郭曉寧.連桿機構的結構運動學特征及參數化實體運動仿真的研究[D].西安：西安理工大學，2003.GUO Xiaoning.Research on structural and kinematic characteristics and parameterized solid kinematic simulation of linkages[D].Xi’an：Xi’an University of Technology，2003.（in Chinese）

[8]衛江紅.基于SolidWorks的連桿機構的運動分析與仿真[D].大連：大連理工大學，2006.WEI Jianghong.Kinematic analysis and simulation of the linkages mechanism based on SolidWorks[D].Dalian：Dalian University of Technology，2006.（in Chinese）

[9]焦麗麗，張達明.UG在機構運動分析應用中關鍵技術的研究[J].機械設計與制造，2009（5）：94-96．JIAO Lili，ZHANG Daming.Research on key technologies of using UG software in the application of motion analysis[J].Machinery Design and Manufacture，2009（5）：94-96.（in Chinese）

[10]劉鴻恩，張列平.質量功能展開(QFD)理論與方法研究進展綜述[J].系統工程，2002，18（2）：1-6.LIU Hongen，ZHANG Lieping.Review on QFD theory and method research progress[J].Systems Engineering，2002，18（2）：1-6.（in Chinese）

[11]孫玲玲.基于QFD和DOE的產品優化設計研究[D].杭州：浙江大學，2011.SUN Lingling.Research of product optimization design based on QFD and DOE[D].Hangzhou：Zhejiang University，2011.(in Chinese)

[12]羅世彬，羅文彩，王振國.基于試驗設計和響應面近似的高超聲速巡航飛行器多學科設計優化[J].導彈與航天運載技術，2003（6）：2-9.LUO ShiBin，LUO Wencai，WANG Zhenguo.Design of experiment and response surface approximation methods in multidisciplinary design optimization for hypersonic cruise vehicle[J].Missles and Space Vehicles，2003（6）：2-9.(in Chinese)

[13]趙妙霞，蔣鈞鈞.機械精度設計中機械制造系統誤差的特征分布[J].甘肅工業大學學報，2001（4）：37-39.ZHAO Miaoxia，JIANG Junjun.Characteristic error distribution of machine-building system for high precision design[J].Journal of Gansu University of Technology，2001（4）：37-39.(in Chinese)

[14]袁貴星，王平.蒙特卡洛模擬及其在公差設計中的應用[J].天津科技大學學報，2008（2）：60-64.YUAN Guixing，WANG Ping.Monte Carlo simulation and its application in tolerance design[J].Journal of Tianjin University of Science and Technology，2008（2）：60-64.(in Chinese)

[15]龐曉紅.基于Excel的蒙特卡洛法及其在工程設計上的應用[J].漳州職業技術學院學報，2006（3）：20-23.PANG Xiaohong.Monte Carlo simulation based on EXCEL and its application in design[J].Journal of Zhangzhou Technical Institute，2006（3）：20-23.(in Chinese)