基于工程量清單計(jì)價模式下的招標(biāo)評標(biāo)機(jī)制研究

張 雁，方金生，吳照學(xué)

（1.池州職業(yè)技術(shù)學(xué)院，安徽 池州247000；2.安徽農(nóng)業(yè)大學(xué) 工學(xué)院，安徽 合肥230036）

1 引 言

招標(biāo)評標(biāo)工作是一個工程項(xiàng)目能否順利成功實(shí)現(xiàn)的一個重要前提。工程量清單計(jì)價是招標(biāo)人或招標(biāo)人組織的其他技術(shù)力量依據(jù)施工圖紙、統(tǒng)一的計(jì)量規(guī)則以及統(tǒng)一的項(xiàng)目劃分，為投標(biāo)人提供工程量清單。而投標(biāo)人則依據(jù)這個工程量清單這個統(tǒng)一平臺，結(jié)合市場行情、工程實(shí)際情況、自身施工管理水平及各種風(fēng)險，自主填報單價。這樣施工企業(yè)競爭的僅是單價，是綜合管理水平，而不需再考慮工程量計(jì)算風(fēng)險。工程量清單計(jì)價的優(yōu)點(diǎn)如：與國際接軌、能接近標(biāo)準(zhǔn)化操作，提高工作效率；風(fēng)險分擔(dān)、便于項(xiàng)目管理；有利于建筑市場公平競爭等。盡管清單計(jì)價有眾多優(yōu)勢，但是當(dāng)前招投標(biāo)單位與承包商對工程量清單計(jì)價模式缺乏足夠的了解，使得工程量清單計(jì)價模式的推廣及在該模式下的招投標(biāo)過程的過渡時期出現(xiàn)各種問題[1，2]。

2 建立評標(biāo)決策模型

2.1 工程量清單計(jì)價模式影響評標(biāo)因素分析

影響建設(shè)工程施工的因素有很多，其中投標(biāo)報價、與施工組織設(shè)計(jì)是關(guān)鍵因素。投標(biāo)報價的合理性與準(zhǔn)確性、工期的可實(shí)現(xiàn)性、質(zhì)量的優(yōu)良性和安全措施的可靠性與施工組織設(shè)計(jì)中的工程進(jìn)度計(jì)劃、施工方案、分包計(jì)劃、資源安排計(jì)劃等密切相關(guān)；同時投標(biāo)人施工組織設(shè)計(jì)的先進(jìn)性和合理性也在投標(biāo)報價中得到真實(shí)反映。主材用量所占比重通常高于50%是投標(biāo)報價的重要組成部分。同時企業(yè)信譽(yù)，市場競爭環(huán)境以及投標(biāo)人的經(jīng)驗(yàn)?zāi)芰Χ紩绊懯┕ぴu標(biāo)[3]。

2.2 優(yōu)劣系數(shù)判斷法確定招標(biāo)項(xiàng)目的評標(biāo)方向

優(yōu)劣系數(shù)法(Electre)的特點(diǎn)在于逐步淘汰，其方法為首先依據(jù)一個自定準(zhǔn)則淘汰所有劣方案，之后在留下的方案基礎(chǔ)上，再制定一個新準(zhǔn)則，再依據(jù)新準(zhǔn)則將部分劣方案進(jìn)行二次淘汰，最后綜合選出最為滿意的有效方案。其步驟主要包括：

1.分析方案各評價指標(biāo)，并確定其重要性系數(shù)。

2.數(shù)據(jù)歸一化處理進(jìn)而確定優(yōu)系數(shù)

數(shù)據(jù)歸一化處理的目的是將各個項(xiàng)目不同的計(jì)量單位化為1 ～100 之間的數(shù)量指標(biāo)值。規(guī)定對于目標(biāo)Fk(k=1，2，…P)，maxfik=fipk，maxfik=fisk，待評價指標(biāo)值為yik。用A,B,C 分別表示maxfik=fipk，maxfik=fisk，yik(i 為方案或項(xiàng)目序號或其他數(shù)值)。在參考前人研究的基礎(chǔ)上，結(jié)合筆者前期的研究，得出如下公式：

根據(jù)上式，可得出歸一化數(shù)據(jù)表，用于優(yōu)系數(shù)的計(jì)算。

3.計(jì)算劣系數(shù)

優(yōu)劣系數(shù)法是以優(yōu)劣系數(shù)為計(jì)算依據(jù)逐步淘汰不理想方案，該法可全面比較各個方案的優(yōu)劣，為此，需要將兩個方案的優(yōu)極差和劣極差進(jìn)行對比計(jì)算，并得出劣系數(shù)。所謂優(yōu)極差是指兩方案作比較后，對應(yīng)目標(biāo)中優(yōu)勢目標(biāo)的相差最大數(shù)值；而劣極差是指一方案劣于另一方案的對應(yīng)目標(biāo)的相差最小數(shù)值。優(yōu)極差與劣極差之和除劣極差，商即為劣系數(shù)，用公式可表示為，其中Dij為方案i劣于方案j 的劣系數(shù)，L1為優(yōu)極差，L2為劣極差。從式中可以看出，1 和0 是優(yōu)系數(shù)與劣系數(shù)的最優(yōu)標(biāo)準(zhǔn)，但在實(shí)際決策中,這一標(biāo)準(zhǔn)無法實(shí)現(xiàn),于是逐步降低標(biāo)準(zhǔn)，獲得最貼近實(shí)際的數(shù)值并制定淘汰方案。我們可以將優(yōu)系數(shù)與劣系數(shù)規(guī)定某個數(shù)為標(biāo)準(zhǔn)，來進(jìn)行逐步的淘汰,最后剩下來選定最優(yōu)的項(xiàng)目。

2.3 層次分析法確定各評價指標(biāo)的權(quán)重層次分析法一般可按以下步驟解決問題。

1.遞接層次結(jié)構(gòu)的建立

分解復(fù)雜問題，劃分成元素單元。將這些元素的屬性作為基礎(chǔ)，劃分成不同層次。將基準(zhǔn)定位某同層元素，可對下層某些元素支配，同時上層元素可支配本層元素。這種關(guān)系一般由準(zhǔn)則層、目標(biāo)層、指標(biāo)層等組成由上至下形成遞接關(guān)系[4，5]。

2.構(gòu)造兩兩比較判斷矩陣

將某一層指標(biāo)（用V 表示）確定，設(shè)V1，V2…Vn為它所支配的下一層次指標(biāo)。本文建立的目標(biāo)是按各指標(biāo)V1從對于指標(biāo)V 的相對重要性賦予V1，V2…Vn又相應(yīng)的指標(biāo)權(quán)重。采用兩兩比較法求得權(quán)重[6]，這樣，對于指標(biāo)V，n 個子指標(biāo)構(gòu)成的判斷矩陣

其中Vij就是指標(biāo)Vi對指標(biāo)Vj相對于指標(biāo)V的重要性標(biāo)度，且有以下性質(zhì)：

Vijφ0，Vij=1/Vji，當(dāng)i=j 時,Vij=1

3.指標(biāo)權(quán)重的確定

指標(biāo)V 的判斷矩陣為A, 假定有n 個評價指標(biāo)V1，V2，…，Vn，分別求出它們對于指標(biāo)V 的權(quán)重w1，w2，…，wn，向量形式采用w=(w1w2,……wn)T,w 值有求和法、根法、征根法、小二乘法等計(jì)算方法。其中特征根法應(yīng)用最廣泛，同時又有重要的理論意義。其思路為解判斷矩陣A 的特征根：

此處λmax是A 的最大特征根，W 為特征向量,權(quán)重向量則為所得到的特征向量W 經(jīng)歸一化后的結(jié)果。在數(shù)值計(jì)算時，可以直接采用目前已經(jīng)成熟和普及的Matlab 數(shù)學(xué)工具，使用調(diào)用函數(shù)命令“（V，D）=eig（A）”可以高效、直觀得出λmax及W=（w1，w2，…，wn）T之后對W 歸一化處理,得到各指標(biāo)的權(quán)重[5]。

4.檢驗(yàn)判斷矩陣的一致性

為保證目標(biāo)權(quán)重向量的合理性與準(zhǔn)確性，需要對判斷矩陣進(jìn)行一致性檢驗(yàn)。人自身的局限性使得在兩兩比較時會出現(xiàn)偏差，為避免誤差過大，則必需檢驗(yàn)判斷矩陣A 的一致性。

計(jì)算一致性指標(biāo)CI(Consistent Index)：

當(dāng)λmax=n，CI=0，為完全一致；判斷矩陣的一致性與CI 值成反比關(guān)系，CI 值越小一致性越符合要求。普遍認(rèn)為，判斷矩陣一致性在CI≤0.1 范圍內(nèi)可以接受，反之要重新兩兩比較。當(dāng)判斷矩陣的階數(shù)n越高時（即兩兩比較的因素越多時），CI 值會由于人為造成的偏差過大，將導(dǎo)致無法滿足一致性。這時,可將判斷矩陣一致性的要求降低, 引入平均隨機(jī)一致性指標(biāo)RI(Random Index)。

進(jìn)而得出一致性率CR(Consistency ratio)：

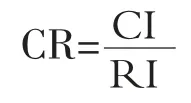
當(dāng)CR＜0.1 時，則判斷矩陣的一致性符合要求,當(dāng)CRI≥0.1 時，則需修正判斷矩陣[7]。

2.4 建立復(fù)合標(biāo)底定標(biāo)決策模型

2.4.1 復(fù)合標(biāo)底定標(biāo)的序列分析方法

復(fù)合標(biāo)底法的標(biāo)價合理性源于中標(biāo)單位兼顧競爭對手的態(tài)勢以及投標(biāo)單位中標(biāo)后的隱患與自身能力。同時投標(biāo)經(jīng)驗(yàn)與投標(biāo)目的需要投標(biāo)單位進(jìn)行科學(xué)預(yù)測與數(shù)量分析時慎重考慮。本文建立的復(fù)合標(biāo)底的投標(biāo)報價數(shù)學(xué)模型是以序列分析法為基礎(chǔ)[8]。

2.4.2 復(fù)合標(biāo)底定標(biāo)的決策模型的建立

假設(shè)X 為最優(yōu)報價；K 為復(fù)合標(biāo)底的下降率（即下降K 成為最高得分點(diǎn)）；D 為模擬甲方的計(jì)算標(biāo)底；Y 為甲方評標(biāo)時的綜合標(biāo)底；D 占Y 的權(quán)數(shù)設(shè)為W；H 為所有有效投標(biāo)價的平均值。則最優(yōu)報價為

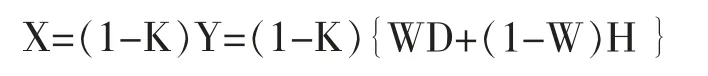
X 函數(shù)是有極限的，且存在最優(yōu)解。由于投標(biāo)報價存在競爭性，則其最優(yōu)解為最小極限值。

從競爭對手的歷史報價資料中比較容易獲得H值。可在模擬中忽略報價偏差大和競爭力弱的單位。一個有經(jīng)驗(yàn)，能力強(qiáng)的投標(biāo)人，其投標(biāo)報價總趨近于復(fù)合標(biāo)底的最優(yōu)分值。X 與H 的關(guān)系是投標(biāo)人的多次復(fù)合[9，10]。經(jīng)計(jì)算，當(dāng)確定數(shù)值X' 為X1，X2，…，Xn序列值的穩(wěn)定值，則X' 可認(rèn)為是序列分析的結(jié)果，即為最優(yōu)報價。公式如下：

Xi+1+1=(Xi)

合并計(jì)算，則有

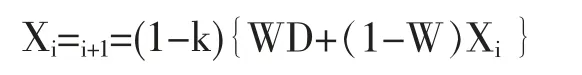
通過類推可以得到如下規(guī)律：

當(dāng)i=n-1 時，

Xn=(1-k) WD+（1-W）Xn-i｝=mxD+ymXn-1

=mxD+xym2D+xy2m3D+xy3m4D+…+xyn-2mn-1D+yn-1mnD+ynmn+1D

｛

當(dāng)i=n 時，Xn+1=(1-k) ｛WD+（1-W）Xn｝

=mxD+ymXn

=mxD+xym2D+xy2m3D+xy3m4D+…

+xyn-2mn-1D+ynmn+1D

式中，m=1；x=W；y=1-W。由于y＜1，則當(dāng)n 趨近于無窮大時，yn是無窮小數(shù)，則可以忽略其對最終投標(biāo)報價值的影響。故令Xn+1=Xn，則有g(shù)=(x)=Xn+1-Xn=0，即

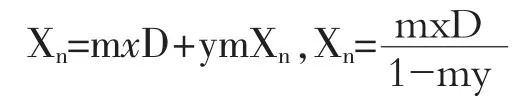
則最優(yōu)報價Xn為

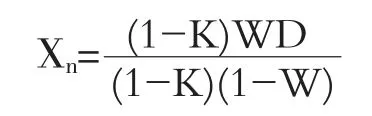
公式中的K，W 一般都為已知，因此要得到比較準(zhǔn)確的最優(yōu)報價，要求比較準(zhǔn)確的估計(jì)業(yè)主的標(biāo)底D。

3 結(jié) 語

本文分析了清單計(jì)價模式下常用評標(biāo)方法的優(yōu)缺點(diǎn)，綜合考慮對評標(biāo)過程中的產(chǎn)生影響的各種因素，并對其影響程度進(jìn)行分析。進(jìn)而提出清單計(jì)價下招標(biāo)評標(biāo)機(jī)制的全新模型，優(yōu)化當(dāng)前評標(biāo)常見的各種方法，可為招投標(biāo)交易中心、工程咨詢機(jī)構(gòu)等部門的招標(biāo)評標(biāo)工作提供一定的技術(shù)指導(dǎo)，并為進(jìn)一步的研究提供了必要的理論依據(jù)。

[1]徐曉燕.工程量清單計(jì)價模式下招投標(biāo)階段的造價控制[J].山西建筑，2005(31):1-2.

[2]陳宏華.價值工程在政府投資工程項(xiàng)目中的應(yīng)用研究[D].無錫：江南大學(xué)，2009：1-3.

[3]程鴻群,王先甲，等.基于工程量清單計(jì)價模式的建設(shè)工程施工評標(biāo)多目標(biāo)決策[J].武漢大學(xué)學(xué)報(工學(xué)版)，2005（2）:2-3.

[4]張曼.工程量清單計(jì)價模式下工程造價控制[J].山西煤炭管理干部學(xué)院學(xué)報，2009(3)：49-50.

[5]潘登.工程承包商投標(biāo)風(fēng)險管理研究[D].長沙：湖南大學(xué)，2008：28-23.

[6]吳高莉.建設(shè)工程施工項(xiàng)目評標(biāo)決策支持系統(tǒng)研究[D].武漢:武漢理工大學(xué)，2006：32-33.

[7]付厚利，岳慶霞.深表土復(fù)雜荷載條件立井井壁可靠性的模糊綜合評價[J].巖土力學(xué)，2003(25):2-3.

[8]臧海波.工程項(xiàng)目競爭新思路研究[D].鎮(zhèn)江：江蘇大學(xué)，2010：49-50.

[9]高萍莉.工程量清單計(jì)價模式應(yīng)用過程中相關(guān)問題研究[D].重慶：重慶大學(xué)，2007：19-20.

[10]王春海.建設(shè)項(xiàng)目施工階段造價控制方法的研究與應(yīng)用[D].西安：西安建筑科技大學(xué)，2005：58-59.