具奇異非線性項p－Laplace方程Dirichlet問題解的存在唯一性

陳雨彤， 魏公明

（上海理工大學 理學院，上海 200093）

長期以來，非線性橢圓問題一直受到人們的廣泛關注，其原因是許多數學物理問題，如源于非線性源的非線性擴散理論、量子場論、統計力學以及星系的重力平衡理論與非線性橢圓問題有極大的聯系.而且數學內部的許多分支，如幾何學中的Yamabe問題和等周不等式、調和分析中的 Hardy－Littlewood－Sobolev不等式、Yang－Mills泛函的非極小解的存在性與非線性橢圓問題有著深刻的聯系.國內外關于非線性橢圓型方程可解性的研究較廣泛，解決這類問題的方法主要有不動點定理、上下解方法、拓撲度理論、隱函數（組）定理、橢圓正則化方法、緊微法、變分法等.

具奇異非線性項橢圓型方程Dirichlet問題是偏微分方程領域的重要研究內容.許多學者對奇異非線性橢圓型方程Dirichlet問題解的存在性和唯一性作了深入的研究.Crandall等［1］研究了下列非線性邊界值問題

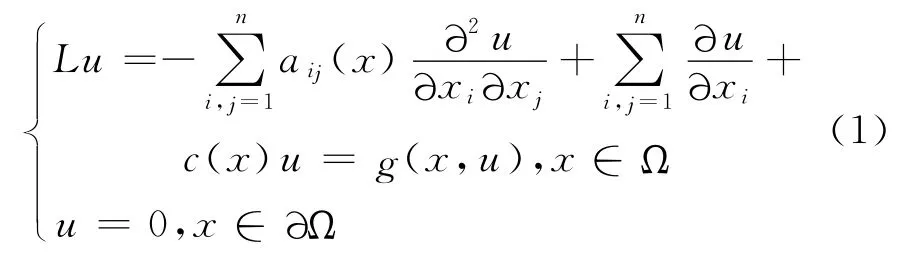
得到了方程解的存在性，得到式（1）的古典解u∈C2（ ）Ω ∩C Ω（ ）— 存在且唯一，且在Ω 中u＞0.Fulks等［2］得到了下列問題的解的存在性

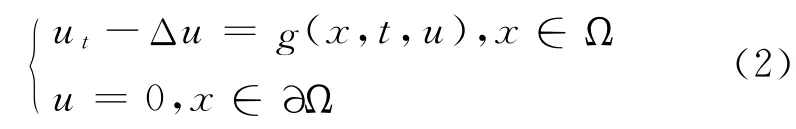
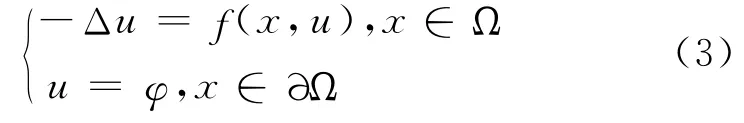
的解的存在性.Cocite等［4］得到了下列問題的解的存在性

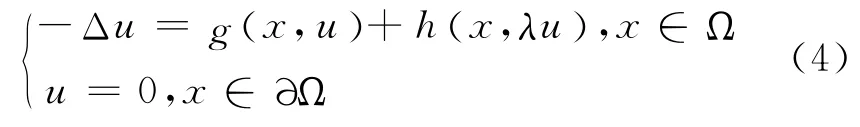
然而，近年來非線性邊界值問題已被廣泛研究，對于p－Laplace算子的非線性邊界值問題的研究已有許多結果，如文獻［5—8］.文獻［9—10］具有相同的特點，即在u＝0處非線性項是奇異的，邊值問題的解在所定義的區域中是嚴格正的，即u＞0.

本文研究下列形式的非線性橢圓邊界值問題

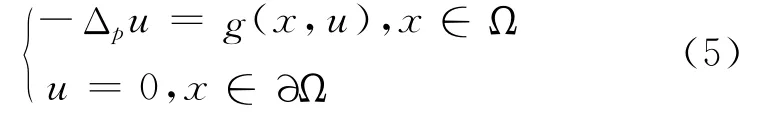
式中，Ω 是?n中的有界光滑開區域，?Ω 是Ω 的邊界，且?Ω 是C1階的，p＞1.

本文主要研究式（5）的解的存在性，給出下列假設：

本文的主要結果為：

定理1 假設條件（g1）和（g2）成立，則式（5）存在唯一解且在Ω 中u＞0.

1 重要命題和引理

在本節，將給出一些為了證明定理1而需要的命題和引理.

定義1 u∈W1，p（ ）Ω 是式（5）的弱解，若對任意的η∈C∞0（ ）Ω 有

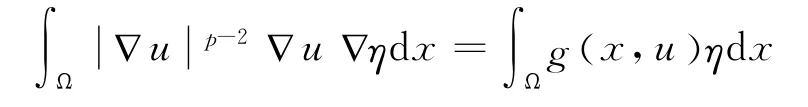
Sobolev嵌入定理［11］設Ω??n是有界光滑開區域其中

定義2［12］函數是式（5）的一個上解，如果

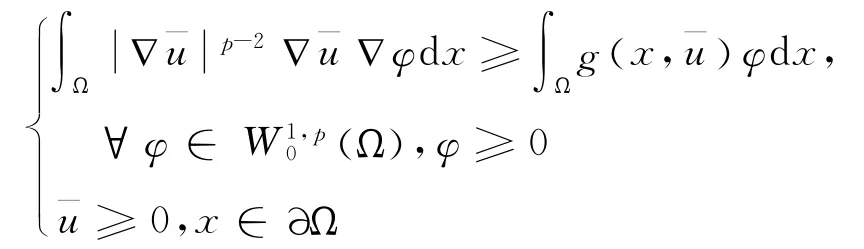
成立.

定義3［12］函數是式（5）的一個下解，如果

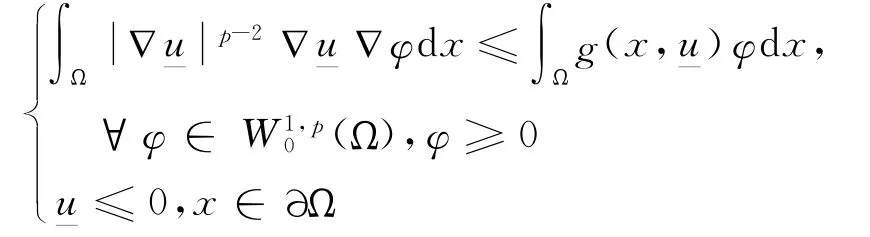
成立.

最大值原理［13］若滿足在Ω 中－Δpu≥0，在?Ω 上u＝0，則在Ω 中u≥0.

強最大值原理［13］若在Ω 中－Δpu≥0，在?Ω上u ＝0，且在Ω 中u ≠0，則對任意的x∈Ω，u（x）＞0且

弱 比 較 原 理［13］如 果 對 于 任 何u1，u2∈由u2（x∈?Ω）可以推出

為了得到式（5）的解，研究下列問題

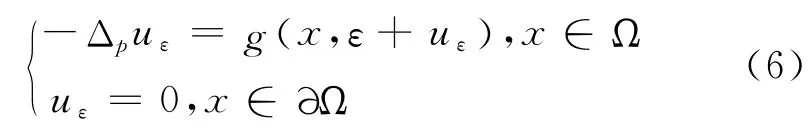
其中ε＞0，則在下面的證明中將會得到當ε→0＋時，uε收斂于式（5）的解u.

引理1 假設條件（g1）和（g2）成立，當x∈Ω時，存在ε0＞0，當0＜ε＜ε0時則

a.式（6）存在唯一正解uε；

b.當0＜ε≤δ＜ε0時，uε≥uδ，且ε＋uε≤δ＋uδ，其中uε，uδ是式（6）的任意兩個解.

證明 因為當0＜ε＜ε0時而對且η≥0，有可知0是式（6）的下解.

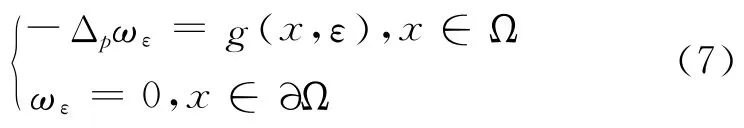
假設式（7）存在兩個解ω1，ω2，當x∈A ?Ω 時，ω1（x）＜ω2（x），則當x∈?A 時，ω1＝ω2＝0，由弱比較原理可知，當x∈A時，ω1≥ω2，故A 為空集.同理可證ω1≤ω2，故ω1＝ω2，因此ωε是式（7）的唯一解.再由強最大值原理可知，當x∈Ω 時

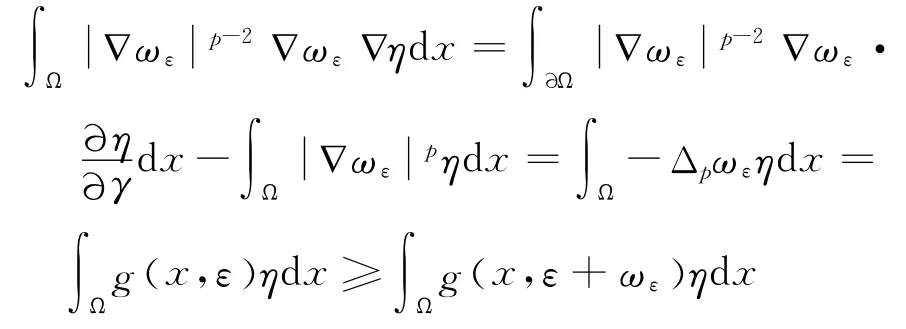
可知ωε是式（6）的上解.

假 設 當 x ∈A ?Ω 時，uε＞ωε，則即－Δpuε≤－Δpωε；當x∈?A 時，uε＝ωε＝0，由弱比較原理知，當x∈A 時，uε≤ωε，故A 為空集.明顯地，0不是式（6）的解，故Ω 中0＜uε≤ωε.因此式（6）的解存在.

接下來證明不等式當0＜ε≤δ≤ε0時，

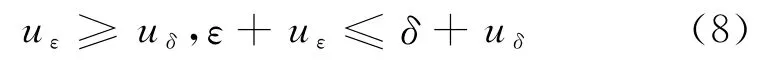
式中，uε，uδ是任意兩個解，令或＝（δ＋uδ）－（ε＋uε）.要證式（8）成立，即證≥0.

由式（8）可知

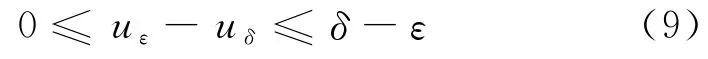
式中，當ε→0＋，δ→0＋時，可知uε＝uδ，故證得解的唯一性.

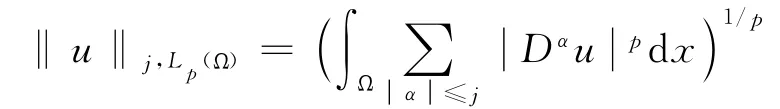
令h ＝（h1，…，hn）是 一個 非 零 向 量，

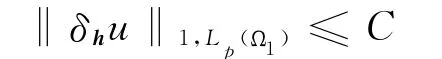
h是任意足夠小的向量，則u∈W2，p（Ω），且

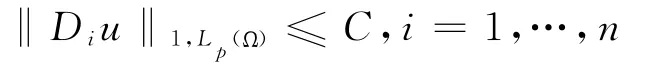
該引理的證明見參考文獻［14］中的引理3.3.

2 定理1的證明

在本節中，運用最大值原理、弱比較原理、引理1和引理2來完成定理1的證明.

由引理2，假設σ1是Ω 中的任意開區域，使得則存在C，使得

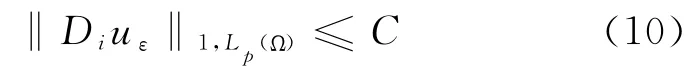
下面證明解的唯一性，假設u，v 是兩個解，當x∈A?Ω 時，，則v），即當x∈A 時，－Δpu≥－Δpv；當x∈?A 時，u＝v＝0，由 弱 最 大 值 原 理 得 到 當x ∈A 時，.由對稱性可證得，則u＝v.定理1證畢.

3 更一般的非線性邊界值問題

將式（5）拓展，研究更一般的非線性邊界值問題

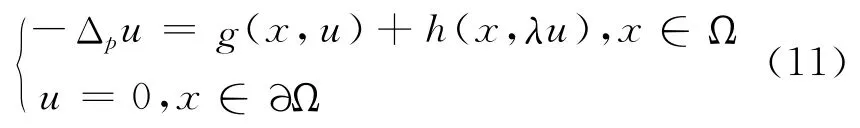
其中λ≥0，Ω 是?n中的有界光滑開區域，h∈.

假設（g1）和（g2）成立，且

假設?Ω 是C1階的，令

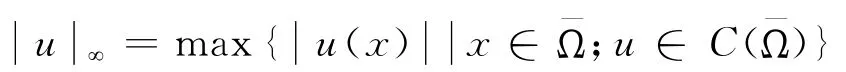
令μ 是

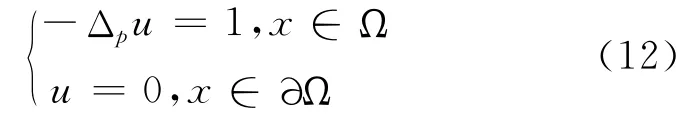
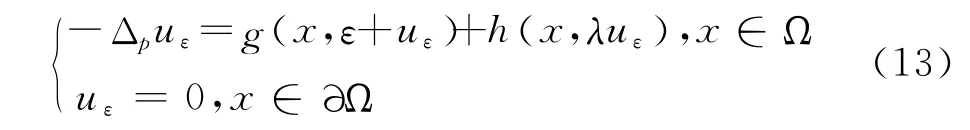
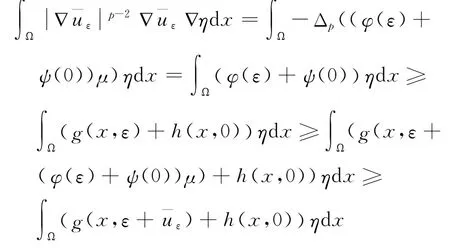
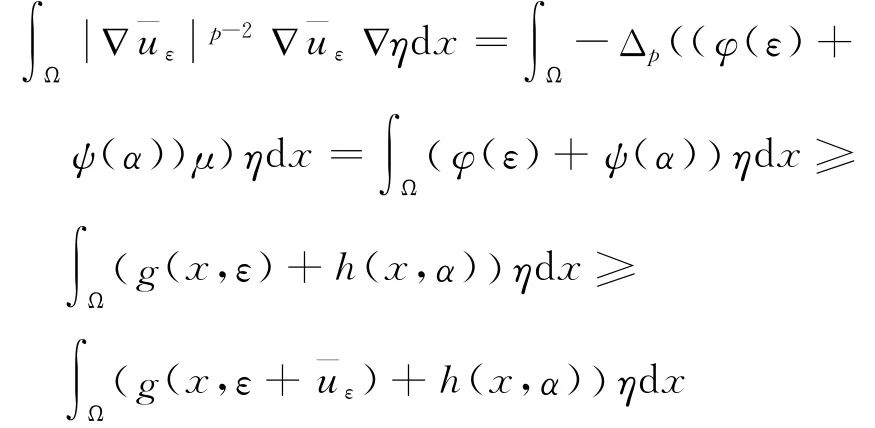
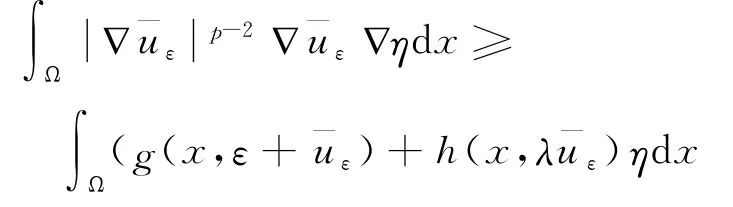
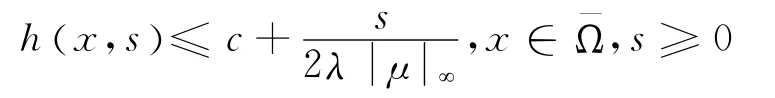
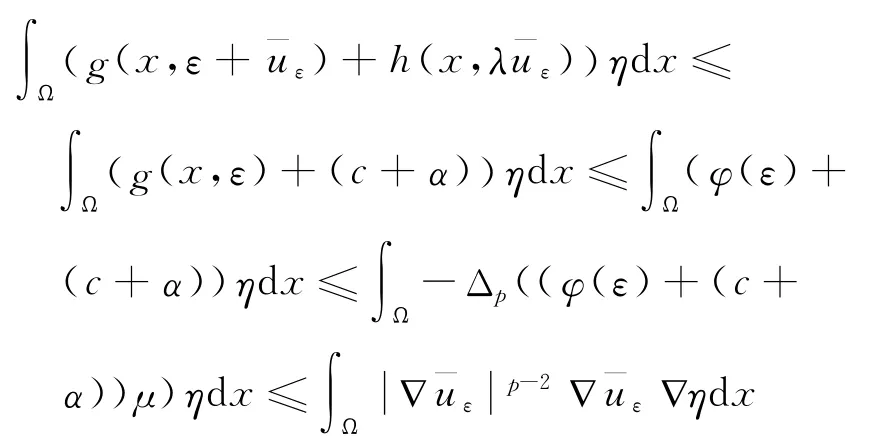
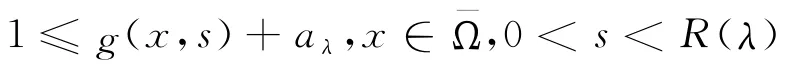
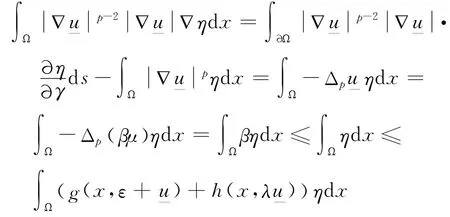
對于0＜ε＜ελ，令當x∈Aε時，對且η≥0有

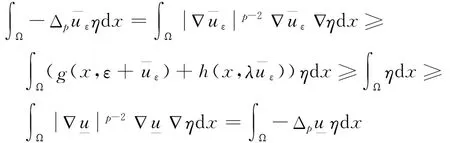
引理5 給予λ∈［0，λ（ g ，h ）），對所有的ε∈分別是式（13）的上下解，并且在Ω 中幾乎處處成立，那么式（13）在區間

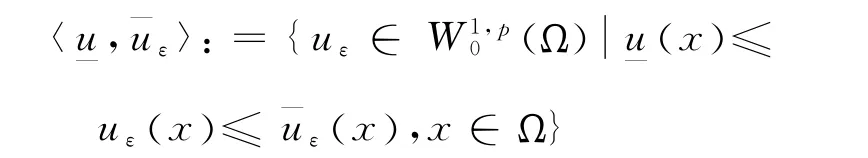
內存在最大值u＊和最小值u＊，即式（13）的每一個屬于的解uε都滿足u＊（x）≤uε（x）≤u＊（x）在Ω 內幾乎處處成立.

該引理的證明參考文獻［12］的294—295頁.

下面來證明定理2.

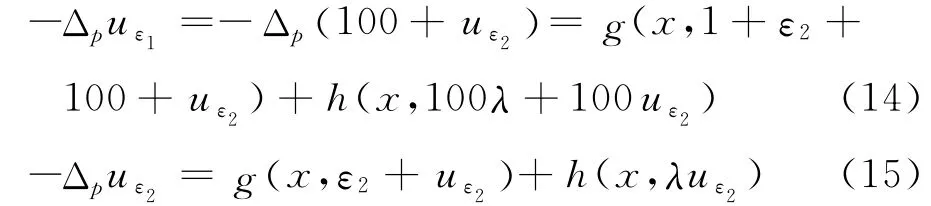
可知－Δpuε1＝－Δp（10 0＋uε2）＝－Δpuε2，而 式（14）與式（15）的右邊不相等，故矛盾.因此，對?η＞0，?δ＞0，當時，由柯西收斂準則可知收斂.由于收斂，對任意的η＞0，當時，｜uε（x＋h）－uε（x）｜＜η，由于h 足夠小，而由前面的引 理2 知uε∈W2，p（Ω ） ，可 選α∈（0 ，1） ，p＞n／（1－α），由Sobolev 嵌 入 定 理 知在C1，α（Ω ） 是 緊 的，因 此 存 在當εm→0時，uεm在中收斂，令是其極限.同樣的，存在，當εm→0 時，在中收斂，即存在，使得.因此可得在W1，p（Ω ） 中分別收斂于u，.

［1］Crandall M G，Rabinowitz P H，Tartar L.On a Dirichlet problem with a singular nonlinearity［J］.Communications in Partial Differential Equations，1977，2（2）：193－222.

［2］Fulks W，Maybee J S.A singular nonlinear equations［J］.Osaka Journal Mathematics，1960（12）：1－19.

［3］Stuart C A.Existence and approximation of solutions of nonlinear elliptic problems［J］.Mathematische Zeitschrift，1976，147（1）：53－63.

［4］Cocite M M，Palmieri G.On a singular nonlinear Dirichlet problem ［J］.Communications in Partial Differential Equations，1989，14（10）：1315－1327.

［5］Bonder F B，Rossi D R.Existence results for the p－Laplacian with nonlinear boundary conditions［J］.Journal of Mathematical Analysis and Applications，2001，263（1）：195－223.

［6］Chipot M，Shafrir I，Fila M.On the solutions to some elliptic equations with nonlinear boundary conditions［J］.Advance in Differential Equations，1996，1（1）：91－110.

［7］Chipot M，Chlebík M，Fila M，et al.Existence of positive solutions of a semilinear elliptic equation inwith a nonlinear boundary condition［J］.Journal of Mathematical Analysis and Zeitschrift，1998，223（2）：429－471.

［8］Terraccini S.Symmetry properties of positive solutions to some elliptic equations with nonlinear boundary conditions ［J］.Differential ＆ Integral Equations，1995，8（8）：1911－1922.

［9］St.Cirstea F－C，Radulescu V D.Existence and nonexistence results for a quasilinear problem with nonlinear boundary conditions ［J］.Journal of Mathematical Analysis and Zeitschrift，2000，244（1）：169－183.

［10］Nowosad P.On the integral equation Kf＝1／f arising in a problem in communications［J］.Journal of Mathematical Analysis and Zeitschrift，1966，14（3）：484－492.

［11］葉其孝，李正元，王明新，等.反應擴散方程引論第一版［M］.北京：科學出版社，2011.

［12］王明新.非線性橢圓型方程［M］.北京：科學出版社，2010.

［13］García－Melián J，de Lis J S.Maximum and comparison principles for operators involving the p－Laplacian［J］.Journal of Mathematical Analysis and Zeitschrift，1998，218（1）：49－65.

［14］Agmon S.The Lpapproach to the Dirichlet problem Part I：regularity theorems［J］.Annalidella Scuola Normale Superiore di Pisa－Classe di Scienze，1959（13）：405－448.