醫院衛生人力成本影響因素的實證研究*

◆任 帥 董曉建

任 帥 董曉建*

第四軍醫大學醫學教育與衛生管理研究中心 陜西 西安 710032

隨著醫療衛生事業的不斷發展，人力成本在醫院總成本中的占比呈現不斷增長的趨勢，所以醫院都在加強人力成本的控制。然而，目前關于衛生人力成本控制方法的研究大多集中于理論探索層面，缺乏實證數據支持，這使得醫院對于人力成本的控制效率大大降低。通過建立醫院衛生人力成本的影響因素模型，從定量分析的角度找出衛生人力成本的影響因素，可以為醫院控制人力成本提供理論與實證依據，提高醫院的運營效率，使醫院在較為合理的人力成本占比水平下提供更好的醫療服務，從而走向優質、高效、低耗的可持續發展道路。本文通過建立衛生人力成本影響因素的回歸模型，探索衛生人力成本的主要影響因素，為人力成本管理提供實證依據。

1 資料與方法

1.1 資料來源

資料來源于某三級甲等綜合醫院36 個月(2008年10月 ～2011年9月)的人力成本相關數據。

1.2 研究方法

1.2.1 指標選擇 本模型所選取的指標都是目前醫院管理的常規指標，包括醫院總收入、住院天數、住院人數、手術人次數、出院人數、門診次數、平均住院費用等。醫院衛生人力成本由衛生技術人員的工資費用與加班費用構成。各變量編碼見表1。

從變量的相關系數表(見表2)可以看出，醫院衛生人力成本與其它各個變量之間的相關系數較高，全都大于0.5，這說明它們之間存在著較強的正相關關系。因此，在本模型中，我們可以將醫院總收入、住院天數、住院人數、手術人次數、出院人數、門診次數、平均住院費用以及衛生技術人員數這些因素作為解釋變量，醫院人力成本作為被解釋變量，構建多元線性回歸模型。經過正態性檢驗，顯示醫院人力成本服從正態分布，所以無需對之進行對數轉換。

表1 變量編碼

1.2.2 統計模型的選擇 從變量相關系數表中我們得知，多個解釋變量之間存在著較強的相關關系，即存在多重共線性。所以本文對于多元線性模型的參數估計將采用主成分回歸法來分析各個變量對衛生人力成本的影響程度。因為主成分分析法在處理多變量問題時具有其一定的優越性，其降維的優勢是明顯的，同時主成分回歸法也適用于一般的多重共線性問題，尤其是對共線性較強的變量［1－3］。數據分析由統計學軟件PASW SPSS18.0 完成。

1.2.3 主成分回歸法的基本原理基于主成分分析的思想，W.F.Massy 于1965年提出了主成分回歸，其具體做法是:先對多個自變量做主成分分析，綜合出少數幾個主成分，然后以這幾個主成分為自變量與應變量建立回歸方程。這樣，不但減少了回歸分析中自變量的個數，而且作為自變量的各主成分互不相關，保證了回歸方程的穩定性。同時，由于主成分是各個原始變量的線性組合，因此通過主成分建立的回歸方程實際上也可視為因變量與各原始變量之間的線性回歸方程。這種將主成分分析與多元線性回歸分析結合使用的方法稱為主成分回歸［4－6］。

2 結果與分析

2.1 模型的建立

以醫院人力成本Y 為被解釋變量，醫院總收入X1、住院天數X2、住院人數X3、手術人次數X4、出院人數X5、門診次數X6、平均住院費用X7、衛生技術人員數X8 作為解釋變量，μ 為隨機擾動項，建立多元線性回歸模型如下:

Y = β0 + β1 X1 + β2X2 +β3X3 + β4X4 + β5X5 + β6X6 +β7X7 + β8X8 + μ

2.2 多元線性回歸結果

首先運用最小二乘法(OLS)估計多元線性回歸模型，其結果見表3。

從表3 可以看出，雖然模型的調整可決系數R2 為0.822，可以說明模型的解釋效果較為理想，但是住院天數與住院人數的方差膨脹因子(VIF)均大于10。這說明模型存在著嚴重的多重共線性，而且住院人數與門診次數的回歸系數符號與實際意義不符。因此，下面我們運用主成分回歸法對此多元線性回歸模型進行參數估計。

2.3 主成分回歸結果

對醫院總收入(X1)、住院天數(X2)、住院人數(X3)、手術人次數(X4)、出院人數(X5)、門診次數(X6)、平均住院費用(X7)、衛生技術人員數(X8)這8 個變量進行主成分分析，得到各個主成分的累計比例，結果見表4。

表2 變量相關系數表

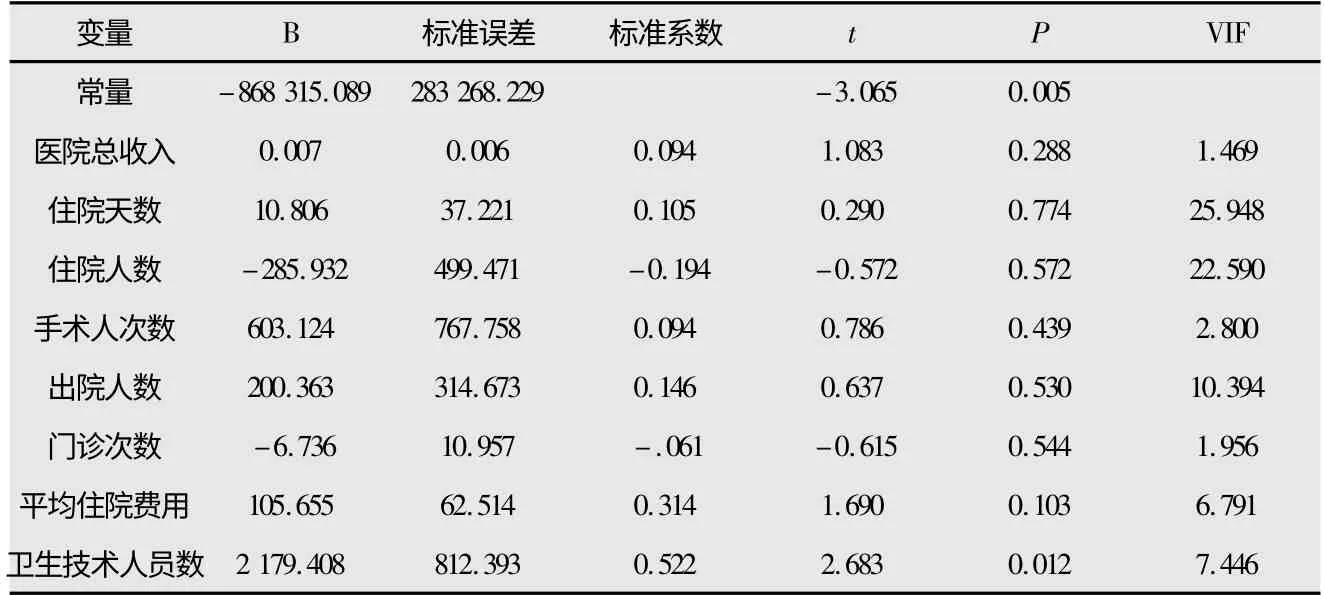
表3 回歸結果

由表4 可見，當選取前5 個主成分時，累計解釋的方差比例達到了97.654%，因此選用前5 個主成分進行分析比較符合實際情況。表5 是所選取主成分的因子載荷陣。

表4 解釋的總方差

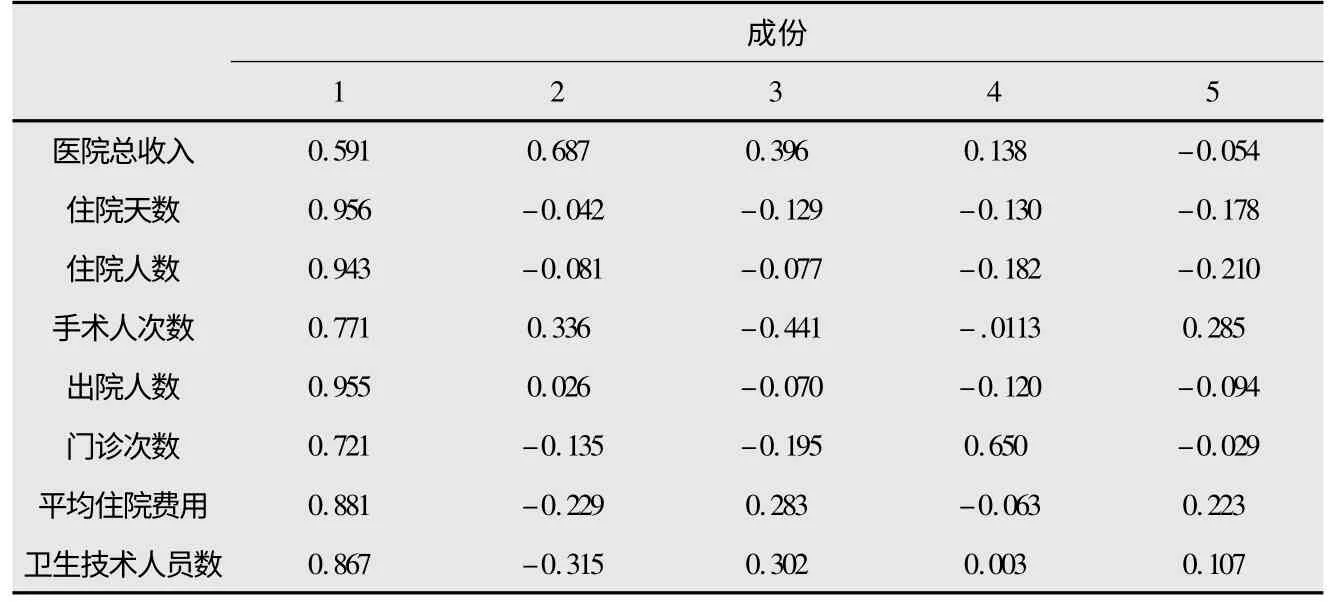
表5 因子載荷陣

結合特征值 λi 與因子載荷陣(qij)，通過公式aij= qij/√(λi)，可以計算出特征向量，即主成分得分系數矩陣。計算結果如表6。

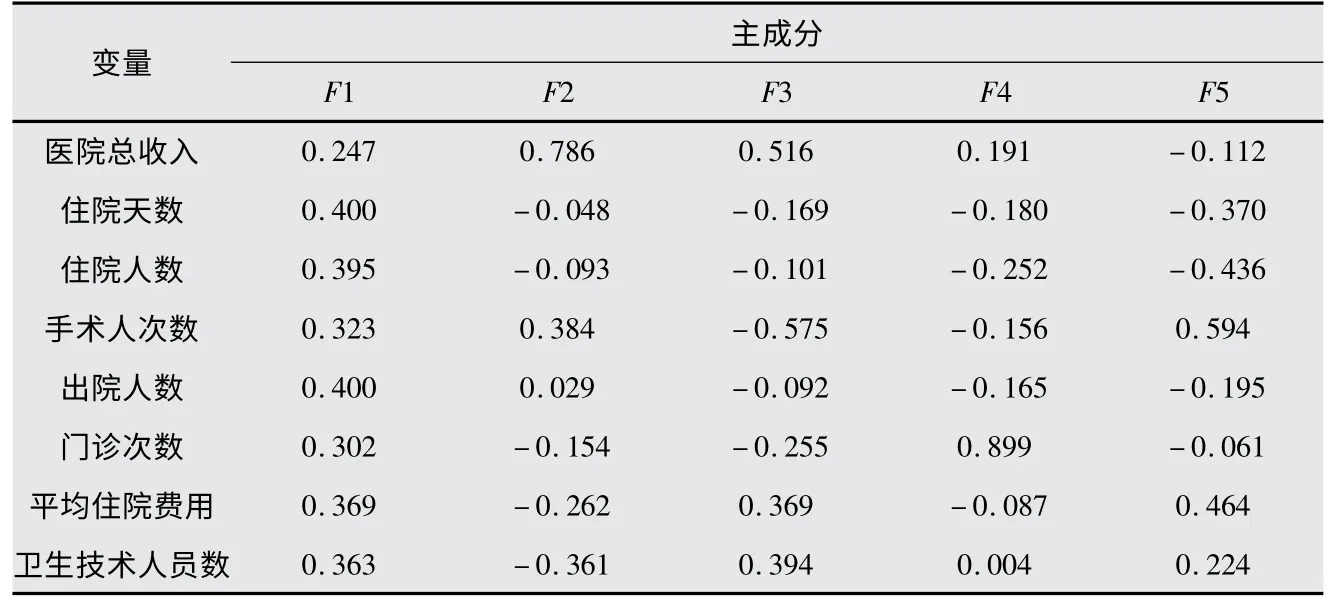
表6 主成分系數矩陣

對于原始變量測定值進行標準化，再根據公式Fi = ∑aijZ(Xj)，就可以計算出這5 個主成分的得分。下面以F1、F2、F3、F4、F5 為解釋變量，以人力成本的標準化變量Z(Y)為被解釋變量，進行逐步回歸分析，模型擬合結果見表7。

表7 回歸系數估計結果

計算結果顯示，5 個主成分中F1、F3、F5 進入了模型，擬合的主成分回歸方程為:Z(Y)= 0.364F1+0.320F3 +0.329F5，模型調整可決系數R2= 0.828，說明模型擬合效果較好，而且回歸系數都通過了顯著性檢驗。將F1、F3、F5 的表達式帶入上述模型，可以得到標準化回歸模型，再將其轉換為一般線性回歸模型，結果為:

Y =－792137.46 +0.016X1－3.077X2－47.225X3 +828.045X4+ 71.208X5 + 0.915X6 + 136.217X7 +1385.119X8

3 討論

3.1 結果分析

從主成分回歸結果來看，5 個主成分已經包含了8 個自變量信息的97.65%，大于80%，達到了主成分回歸的要求。在3 個主成分中，主成分F1 的標準化回歸系數最大，為0.870，說明主成分F1是衛生人力成本的最大影響因素;其次是主成分F3，其標準化回歸系數為0.245;最后是主成分F5，標準化回歸系數為0.158。從表5 因子載荷陣可以看出，主成分F1 在各個影響因素上的載荷都比較大，說明主成分F1 綜合反映了全部指標的信息;主成分F3 在醫院總收入、平均住院費用與衛生技術人員數上的載荷較大;主成分F5 在手術人次數、平均住院費用與衛生技術人員數上的載荷較大。這說明相對于其它原始指標，平均住院費用與衛生技術人員數是對衛生人力成本有著較大影響的因素。但是其余原始指標對于衛生人力成本的影響程度大小則無法明確，有待進一步研究。

3.2 衛生人力成本的控制途徑分析

通過對主成分回歸結果的分析我們發現，衛生技術人員數與平均住院費用是醫院衛生人力成本的主要影響因素。這提示醫院對于此項成本的管理與控制應該從兩方面入手。一方面，醫院要將衛生技術人員的數量控制在一個較為合理的范圍之內，不能盲目擴張或收縮衛生技術人員隊伍規模，否則就將會導致醫院規模效益的下降。另一方面，醫院應該采取有效措施降低平均住院費用，這樣既可以提高醫院的經營效率，又能夠減輕患者的經濟負擔，使醫院與患者實現雙贏。同時，相關研究結果顯示［7－8］，對平均住院費用影響最 大的因素是患者的住院天數，因此可以通過縮短無效的住院天數來減少平均住院費用，進而達到控制衛生人力成本的目的。

4 結語

本文結合多元線性回歸模型，確立了醫院衛生人力成本的主要影響因素，探索了衛生人力成本的有效控制途徑，不僅豐富了研究衛生人力成本的方法和手段，也為我國各級各類醫院合理控制衛生人力成本、提高醫院運營效率提供了可操作的量化依據。

由于本研究僅選擇了一家醫院的樣本數據進行實證分析，一些隱性的因素還未能納入模型，因此在將來的研究中，應該增加更多規模相近醫院以提高代表性，同時應盡可能的收集更多年份、更多種類的數據指標，以使研究結果更加可靠，更具有決策參考價值。

［1］王 靜，李 曼，楊葦葦，等.多元統計方法在住院費用研究中的應用進展［J］.中國衛生統計，2009，26(1):91－93.

［2］蔡善榮，阮紅芳，李 魯，等.以主成分回歸分析方法探討人均衛生費用影響因素的研究［J］.中國衛生事業管理，2001，17(7):399－400.

［3］羅文海，萬巧云，高 永，等.主成分回歸分析與多元線性回歸的對比研究［J］.數理醫藥學雜志，2003，16(2):140－142.

［4］孫振球，徐勇勇.醫學統計學［M］.北京:人民衛生出版社，2005:333－350.

［5］張文彤，董 偉.張文彤.SPSS 統計分析高級教程［M］.北京:高等教育出版社，2004:127－128.

［6］龐 皓.計量經濟學［M］.北京:科學出版社，2007:118－119.

［7］任美璇.基于遞歸系統模型和結構方程模型的參合農民住院費用影響因素分析研究［D］.廣西醫科大學碩士學位論文，廣西:廣西醫科大學，2012.

［8］榮惠英.基于遞歸系統模型的醫保住院費用影響因素研究［D］.山西醫科大學碩士學位論文，山西:山西醫科大學，2011.