偏微分方程解的數值驗算

蔡姝婷

（福建江夏學院 數理教研部，福建 福州 350108）

偏微分方程解的數值驗算

蔡姝婷

（福建江夏學院 數理教研部，福建 福州 350108）

本文提出一種偏微分方程解的數值驗算方法.首先應用有限元的方法求偏微分方程的數值解，然后將偏微分方程的解轉化為一個緊算子的不動點，我們驗證算子在某一個集合中滿足不動點定理，從而偏微分方程的解存在.接著通過分析的方法將不動點定理的條件轉化為計算機可以計算的條件，最后結合區間驗算的方法避免計算機計算過程中存在的截斷誤差，從而證明所求近似解的附近存在精確解.

偏微分方程；數值驗算；不動點定理；區間驗算

1 引言

偏微分方程在自然科學和技術科學領域中都具有很廣泛的應用.在每年的各類型數學建模競賽中，運用偏微分方程進行建模是一種常見的建模方法.如反應擴散型方程中的食餌－捕食者模型，可以模擬兩個不同的種族間的相互作用，其中一個種族捕食另一個種族；Schnakenberg模型描述發育生物學中的一些模式形成等等.如何求這些偏微分方程的解是能否完成一個數學建模過程的重要的問題.到目前為止，能夠運用解析的方法求解的偏微分方程類型相對有限.但是，隨著計算機計算能力的增強以及數值計算方法的發展，偏微分方程的數值解法越來越多，通常運用一些有限元的方法將偏微分方程離散化后進行求解，之后需要求出相應的誤差.有部分的數學軟件如Matlab可以用自帶的軟件包直接進行數值計算，但這樣的數值計算過程都帶有一定的誤差，無法嚴格地證明方程的解確實在某個范圍內是存在的.本文的方法是對傳統的數值計算方法的發展，提出通過數值驗算的方法驗算偏微分方程解的存在性.我們先用有限元的方法求出偏微分方程的數值解，然后將偏微分方程的解轉化為一個方程的不動點，根據不動點定理，驗證在一個小區域內，這個方程的不動點存在.這個驗證的過程是通過計算機來完成的，而計算機在內部計算的過程中，存在一定的截斷誤差，我們應用區間演算[1]的方法來避免這個誤差.整個計算過程我們將在Matlab上實現.通過我們的方法，一方面可以得出方程解的大致形態，另一方面，也可以用計算機進行嚴格的證明解確實是存在的以及解所存在的小范圍.

我們選取較為簡單的偏微分方程說明本文的方法.考慮具有Dirichlet邊界條件的偏微分方程

其中Ω=(0,1)×(0,1),f(x,y)是關于x,y的函數，d是一個常數.

方程(1)近似解的求法有很多種，在[2]中介紹了多種求解偏微分方程數值解的有限元方法.本文同樣將應用有限元的方法求解方程(1),只是對于基函數的選取有所不同.

首先，對于任意的整數m，我們定義Hm=Hm(Ω)為m階的L2-Sobolev空間.同時我們定義H01:=H01(Ω):={u∈H1|u=0 on Ω}，并具有內積〈?,ψ〉=(▽?,▽ψ)，其中(·,·)表示L2(Ω)空間上的內積.我們考慮方程（1）在H01空間中解的存在性.

我們選取基函數φi1i2為

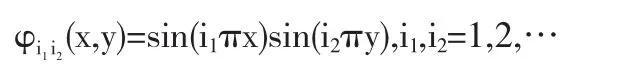
對于一個固定的非負整數N，我們按以下規則對基函數重新排序，

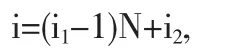
從而基函數成為

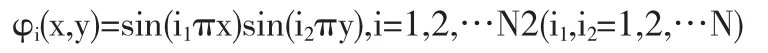
假設H01中的所有元素ψ可展開為傅利葉級數

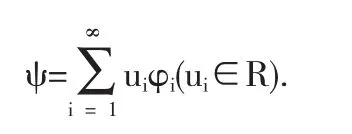
選取適當的N，我們在有限維空間

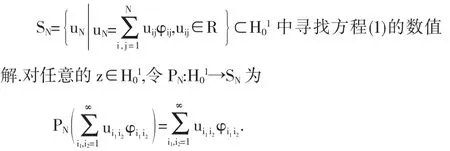
2 近似解

在這一節中，我們將在空間SN中計算方程(1)的近似解.對任意的vN∈SN令

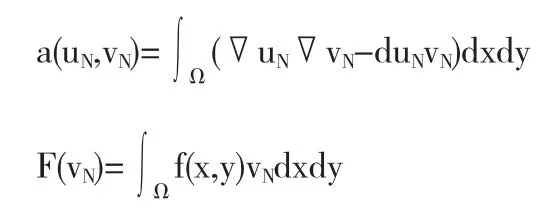
因此我們現在的問題是，求uh∈Sh,使得

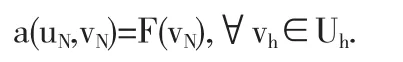
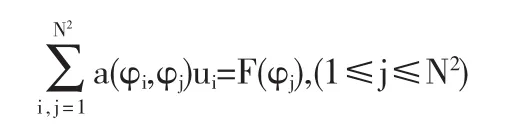
將上述問題寫成矩陣形式，即

其中

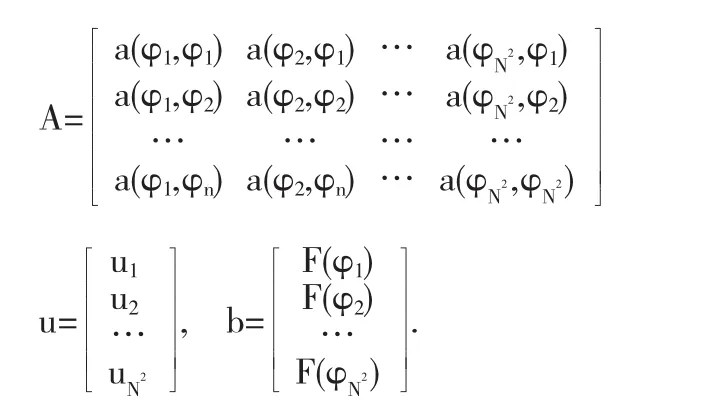
我們運用Matlab即可求出方程(1)的數值解.

3 解的數值驗算

我們知道對于任意的ψ∈L2(Ω)下列的泊松方程存在一個唯一的根?∈H1∩H'0：

將方程(2)的解記為?=L-1ψ則L-1:L2→H01是一個緊算子.

令K(u):=L-1(f(x,y)+du),那么K是H01上的緊算子，并且方程(1)的解為算子K的不動點：

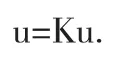
因此由Schauder不動點定理，如果我們能在H01中找到一個非空的，有界的，凸的閉集合滿足

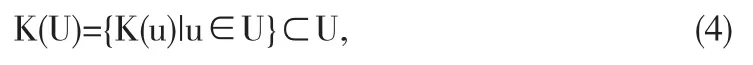
那么在K(U)中就存在一個元素u使得u=Ku.我們的做法是在計算機中構造一個侯補的集合U=UN⊕U⊥,其中UN?SN,U⊥?SN⊥.這里SN⊥表示SN在H01空間中的正交補空間.這樣，我們可以將驗證條件(4)轉化為

Moore在[1]中介紹了區間演算的方法.由于在計算機計算的過程中存在截斷誤差，比如在數學軟件Matlab中，以雙精度符點型數據進行計算，當我們計算1/3時，計算機內部以64位小數進行計算，截斷了小數點后的值，由此產生了誤差.我們應用區間演算來避免這種誤差，如同樣計算1/3時，計算機內部以[0.33333333333333,0.33333333333334]計算.此時既有1/3落于這個小區間內，避免了截斷誤差，同時這個區間的范圍較小，滿足一定的精度要求.為了計算的順利進行，我們定義了區間演算的加減乘除法.對于實數集上的任意兩個區間，X=[a,b],Y=[c,d],我們定義下列運算：

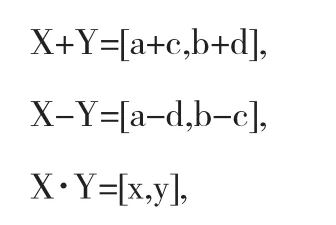
其中x=min{ac,ad,bc,bd},y=max{ac,ad,bc,bd}.同時還定義

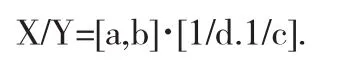
例如：[1,2]·[-2,1]+[0,1]=[-4,3].另外，區間X的幅度定義為：d(X)≡b-a.絕對值為：|X|≡max{|a|,|b|}以及中點為m(X)≡(a+b)/2.Rump根據這些運算規則，在[3]中建立了一個基于區間演算的區間實驗室，實現了在計算機上完成區間演算的過程.

我們這里將用這種區間演算的方法驗證條件(4)的成立.對于條件(4)的有限維部分PNK(U)?UN的驗證，我們把候補集合UN定義為

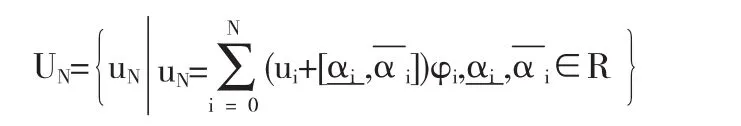
其中Bi是由方程

所確定的.

而對于無限維部分的驗證，我們需要一個引理：

引理1 對任何的?∈H2∩H01,存在一個正常數CN，使得

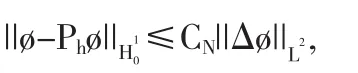
定理1如果

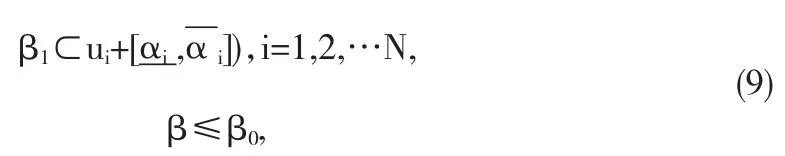
成立，那么在U中存在一個方程K(u)=u的解.

根據這個定理，我們可以得到驗證解存在性的一個算法：

算法1

4 數值結果

我們選取具體的d及f進行計算.若d=1,f(x,y)=x+y.取N=20.我們用Matlab軟件得到方程(1)的近似解如圖1所示.接著利用區間演算實驗室[3]以及算法1進行數值驗算，得到區間長度的最大值為0.004,β0=0.0175.本文所得到的計算結果是在HP ENVY 6 Notebook PC [Intel(R)Core(TM)i5-3317U@1.70 GHz]電腦上用Matlab (Ver.7.0)完成的.

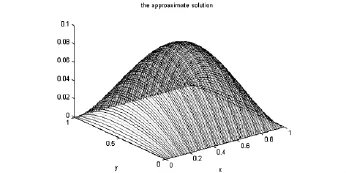
圖1

注：本文的方法針對于相對較為簡單的方程(1)進行求解，具有一定的局限性.如果所遇到的方程關于u是非線性的，同樣是可以用數值驗算的方法進行求解.在求近似解時，可以先用Newton法，而后的數值驗算過程可以采用一種近似的牛頓法，結合不動點定理加以驗證.這是我們今后的研究方向.

〔1〕Moore R.E.Intervalanalysis[M].Englewood Cliffs: Prentice-Hall,1966.

〔2〕馬昌鳳.有限元方法講義[Z].2006.

〔2〕Rump S.M.,INTLAB-INTerval LABoratory[Z],a Matlab toolbox for verified computations,Version 5.5.Inst,Informatic,TU Hamburg-Harburg,http://www.ti3.tuharburg.de/rump/intlab/.

O175.2

A

1673-260X（2015）09-0007-03

本文由教育部留學回國人員科研啟動基金資助項目資助