步進電機計算動詞PID控制系統的設計

鄭雪欽

（廈門理工學院電氣工程與自動化學院，福建 廈門361024）

在高性能的步進電機控制系統中，要求其驅動控制系統具有更好的控制性能和更高的精度，這對步進電機驅動控制系統提出高精度的控制策略要求.步進電機驅動控制過程要求具備精確的系統參數，便于對控制規律進行整定，但是在實際運行過程中，系統參數是變化的，要得到優良的系統性能，需要對驅動控制器進行相應的調整［1］.目前用于實現高精度步進電機控制的方法通常是采用適用于線性控制系統［2］的傳統 PID控制方法［3］，且實現簡單、性能穩定，但對于環境多變、非線性動態系統，卻難以實現對步進電機的在線實時高精度控制［4］.為了實現對步進電機的在線實時自適應控制，在傳統PID控制方法的基礎上，人們引入了一些智能算法，如：神經網絡［5－6］、模糊控制［1］、遺傳算法［7］等來改變 PID控制參數，以提高步進電機控制的魯棒性，但這些智能控制算法較復雜，存在動態響應時間較長，影響系統的響應速度的問題.為了提高步進電機的定位精度、響應速度和抗負載干擾能力，本文在分析計算動詞PID控制的基礎上，設計和構建了步進電機定位控制系統，通過系統仿真和實驗驗證，實現了系統的高精度定位和快速響應.

1 計算動詞PID控制器［8］

計算動詞理論由旅美學者楊濤教授提出，是運用進化函數對人類思維動態建模，將人類專家用動詞描述或執行的動態知識經驗嵌入到機器智能中，是人工智能發展的一個新的系統框架.計算動詞PID控制器結構如圖1所示，結構類似于模糊PID控制器的結構.雖然這兩種控制器結構很類似，但兩者的設計方法大大不同，計算動詞PID控制器中的解動詞化模塊的輸出是動詞“observe”的結果［9］.

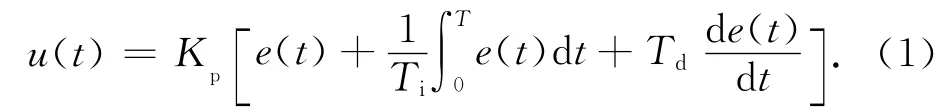
式中：u（t）為控制器的輸出；e（t）為控制器的輸入，它是期望值和被控對象輸出值的差；Kp為控制器的比例系數；Ti是控制器的積分時間常數；Td是控制器的微分時間常數；r（t）是系統期望值.

2 步進電機計算動詞PID控制器的系統設計

2.1 步進電機的數學模型

步進電機電壓方程、轉矩方程和運動方程如下［10］：

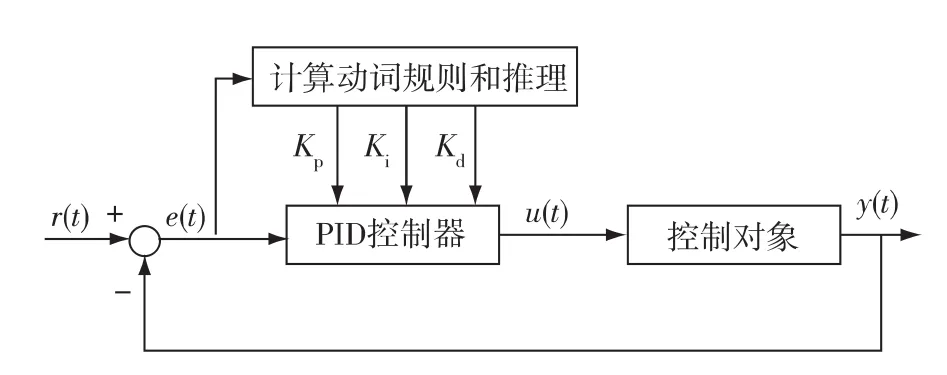
圖1 計算動詞PID控制器結構圖Fig.1 Block diagram of a computational verb PID controller

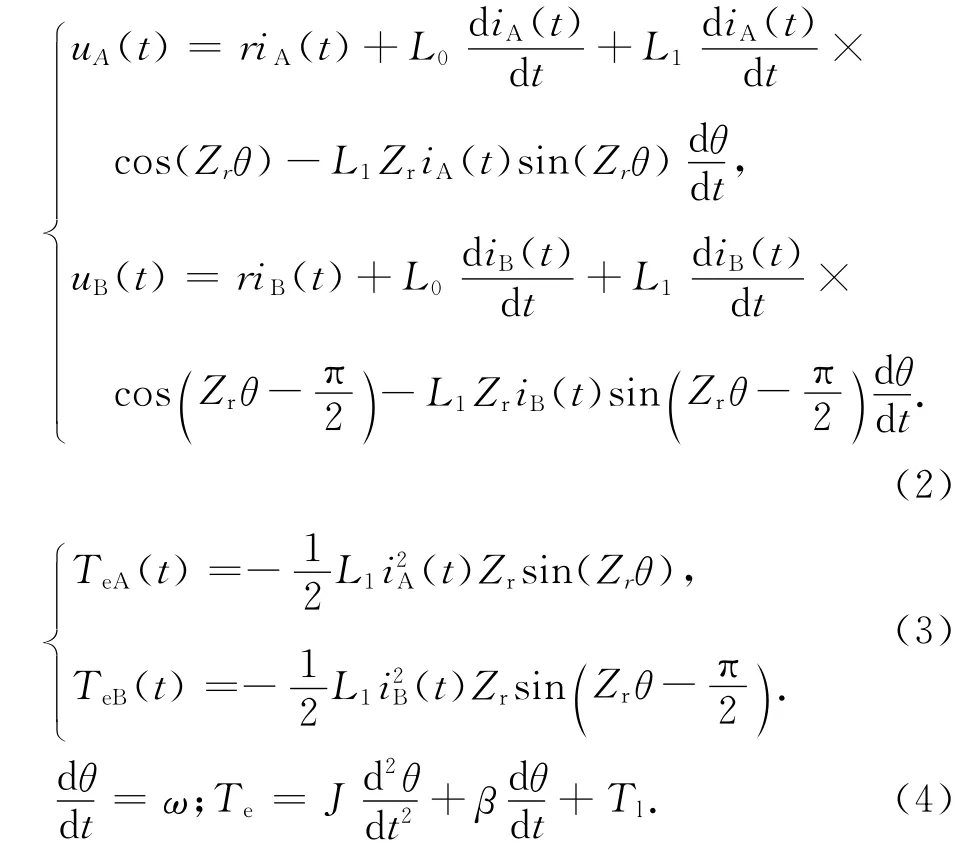
式中，uA（t）、uB（t）為定子兩相電壓；iA（t）、iB（t）為定子兩相繞組電流；r為A相電阻；Zr為轉子齒數；Te為電磁轉矩，是兩個單相繞組產生的電磁轉矩TeA（t）、TeB（t）之和；β為粘滯系數；J為轉動慣量；θ為轉子位置角；L0為自感的恒定分量；L1為自感的基波分量；ω為轉子角速度；Tl為負載轉矩.

2.2 定義誤差絕對值｜e｜的模糊集

根據誤差變化曲線在不同時間段上所對應曲線的相似性，以及模糊集區間的對稱性，對誤差e（t）的模糊集定義可轉化為對誤差絕對值｜e｜的模糊集定義，定義為｛ZO，PS，PM，PB｝.當e（t）成指數穩定地接近0時，由于軌跡在這些區域的時間更長，所以必須更關注接近0的區域.同時把誤差變化規范在［－1，1］內，動詞規則的隸屬度函數和模糊規則的隸屬度函數有所不同，其數學表達式為［9］；

2.3 建立動詞控制規則

根據步進電機定位控制過程、誤差變化情況、PID參數整定規則，計算動詞規則對模糊控制規則進行提取和濃縮，把相同的變化趨勢合并，減少規則數目，用7條計算動詞規則涵蓋了49條模糊控制規則，并應用于控制系統的各個階段.建立如下7條動詞控制規則：

2.4 動詞相似度

在控制過程中，e（t）的變化大部分時間并不是完全等同于控制規則中的前件條件；但反過來說，任一時刻，肯定能在控制規則的前件條件中，找到一個和e的變化趨勢最相似的become.用“動詞相似度”來恒量各個動詞之間的關系，是一個數值，取值范圍［0，1］，相似度越接近1，表示這兩個動詞相似的程度越大；相似度越接近0，則表示越不相像.在動詞控制規則里，可以把前件條件里的7個動詞定義為7個標準動詞，控制過程中觀察到的動詞都和這些標準動詞做比較.所有動詞都可以用become來進行規范化，become的進化函數可表示為

become（state 1，state 2）的時間跨度取Tw，x（t）是觀察到的波形，一個被觀察的動詞的進化函數為

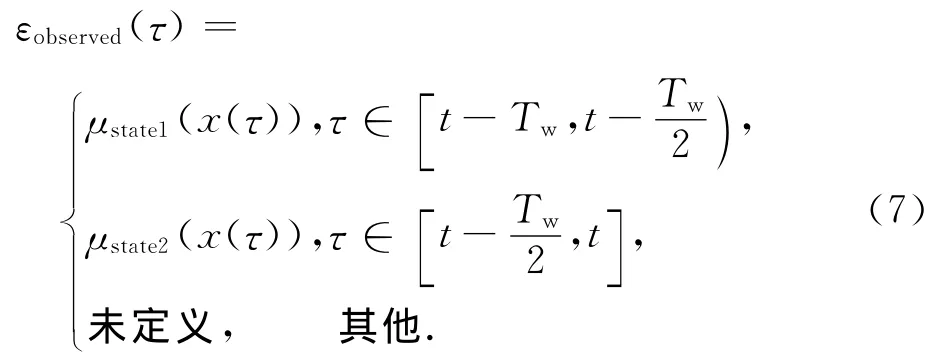
求 “observed”這 個 動 詞 和 become（state 1，state 2）的相似度過程中，首先將Tw分成state 1和state 2兩個區間：

1）在前半個區間求出a1和b1

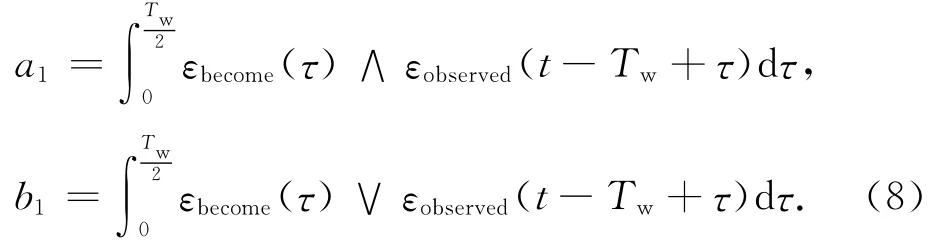
2）在后半個區間求出a2和b2

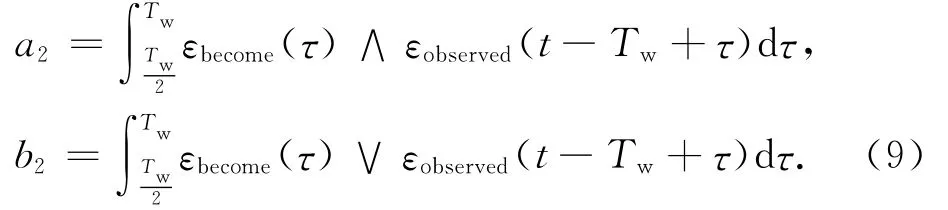
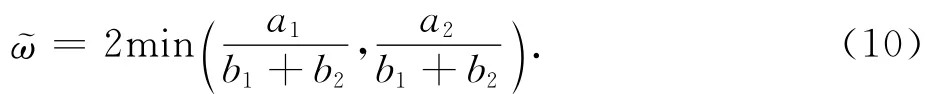
4）在整個Tw范圍內求相似度

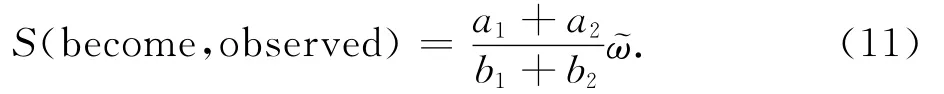
2.5 動詞控制規則的實現

計算動詞規則的推理建立在動詞相似度的基礎上，在控制過程中，觀察控制誤差e的變化趨勢，求出e和標準動詞的相似度.控制器的輸入和輸出都是動詞形式.輸出的動詞Vy是標準輸出動詞以相似度為權的加權平均量.

若x（t）becomexi，則y（t）becomeyi，i＝1，…，n，

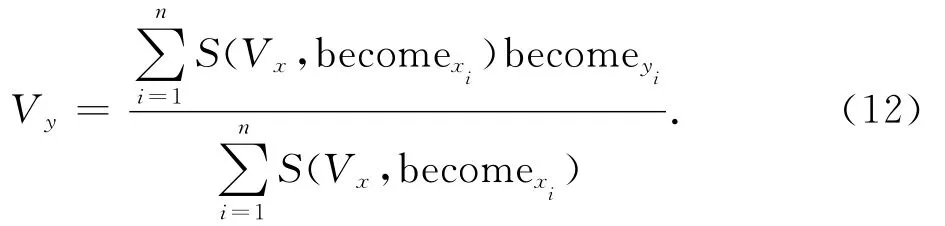
3 仿真分析

在MATLAB中分別建立傳統PID控制器、模糊PID控制器、計算動詞PID控制器步進電機定位控制系統（圖2），由式（1）～（3）建立圖2中“步進電機”模型，3種控制方法結果比較如表1所示.本文所采用步進電機的參數分別為：定子電阻R＝35Ω，定子電感L＝35mH，轉子齒數Zr＝80，轉動慣量J＝0.025kg·m2，阻尼系數Bm＝0.002 5，負載mr＝0～2.5N·m，步進電機功率為0～1W.計算動詞參數：Kp＝0.005，Ki＝0.78，Kd＝0.45；Kp取 值 范 圍：0.004 98～0.005，Ki取值范圍：0.78～0.80，Kd取值范圍：0.45～0.47，仿真結果如圖3所示.

由仿真結果可知，在步進電機定位控制中，采用新型的計算動詞PID控制器，響應曲線優于傳統PID控制器和模糊PID控制器，而且運算速度與傳統PID控制器相當，體現了很好的控制性能.

表1 3種PID控制方法比較Tab.1 Comparison of performance time of the three PID

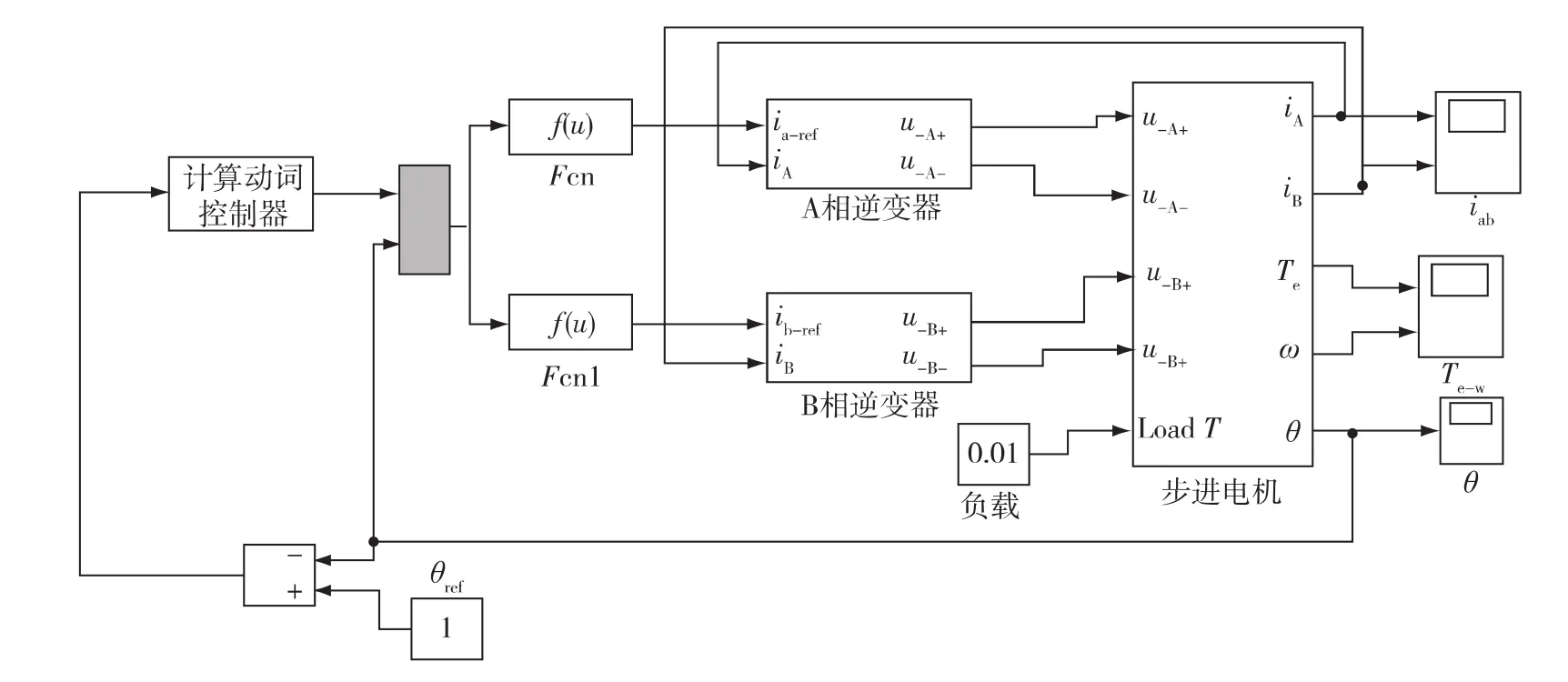
圖2 基于計算動詞PID步進電機定位控制系統仿真模型Fig.2 Simulation model of CVC stepping motor position control system

圖3 控制位置響應曲線Fig.3 Rotor position curve

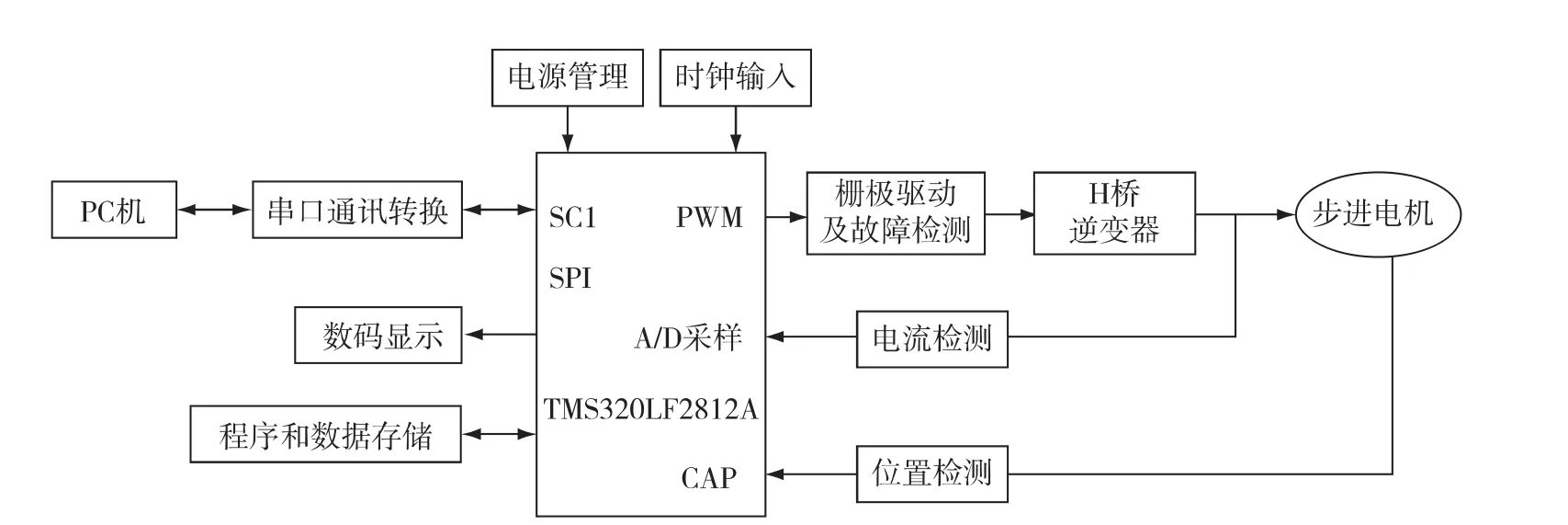
圖4 步進電機定位驅動控制系統Fig.4 Position drive system of stepping motor

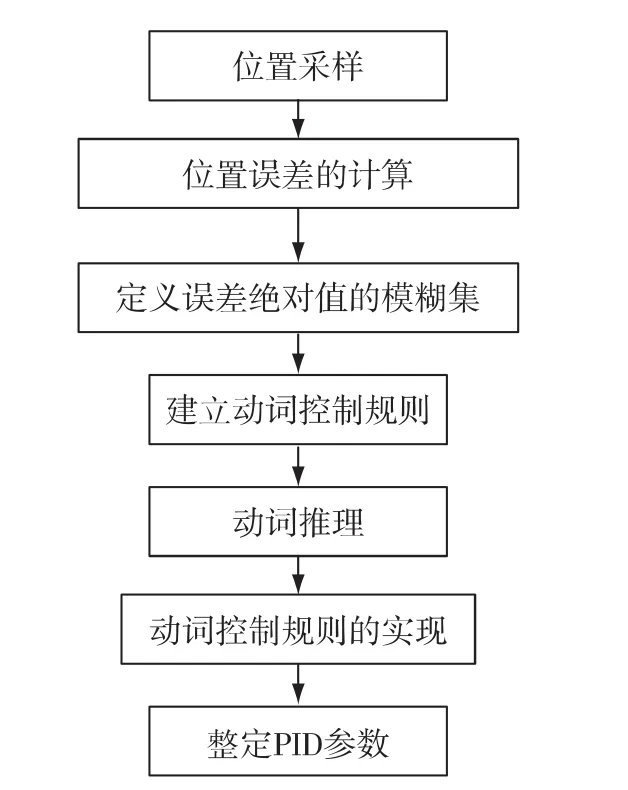
圖5 計算動詞PID控制位置響應曲線Fig.5 Rotor position of computational verb PID

4 實驗驗證

為研究混合步進電機高精度定位系統，測試實際裝置具體性能，驗證本文控制算法實現的可能性，本文完成了基于TMS320LF2812A步進電機定位驅動控制系統的設計，如圖4所示.計算動詞PID控制步進電機位置信號（流程圖如圖5），分別給二相電機繞組通入相應的脈沖寬度調制（PWM）控制信號，實現步進電機的高精度定位控制.步進電機位置響應結果如圖6所示，可以看出實驗結果與仿真結果相一致.

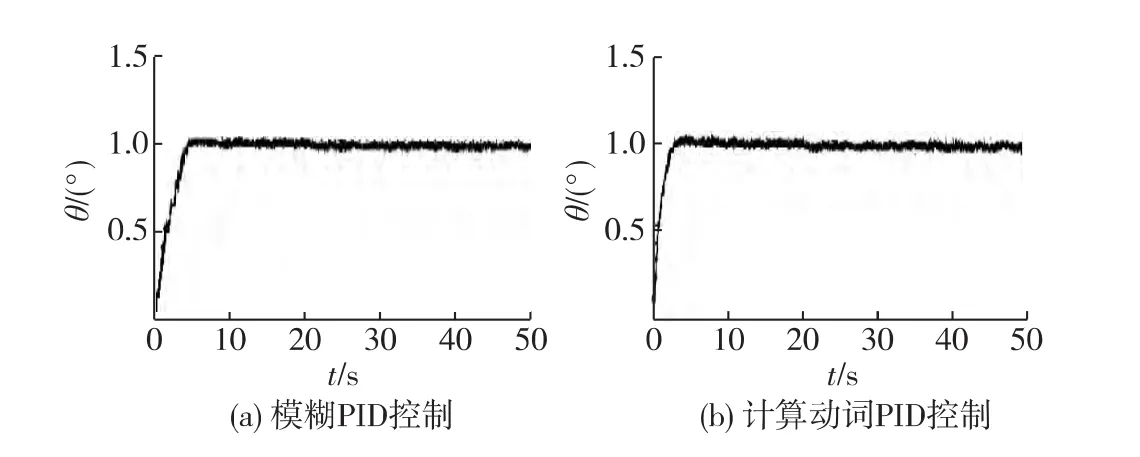
圖6 步進電機定位驅動控制系統Fig.6 Position drive system of stepping motor

5 結 論

本文研究基于計算動詞PID控制器的步進電機智能驅動控制系統，分析了計算動詞PID控制算法的實現，建立了系統的仿真模型和基于TMS320LF2812A步進電機驅動控制系統，仿真和實驗結果表明，在步進電機定位控制系統中，采用計算動詞PID控制，運算時間短、動態響應快、定位精度高，可以保證系統運行的實時性和穩定性.

［1］Betin F，Pinchon D，Capolino G A.Fuzzy logic applied to speed control of a stepping motor drive［J］.IEEE Transactions on Industrial Electronics，2000，47（3）：610－622.

［2］陶永華.新型PID控制及其應用［M］.北京：機械工業出版社，2002：11－15.

［3］史敬灼.步進電機伺服控制技術［M］.北京：科學出版社，2006：24－31.

［4］Wale J，Pollock D.Hybrid stepping motors and drives［J］.Power Engineering Journal，2001，15（1）：5－12.

［5］Shi J Z，Xu D G，Wang Z P.A Novel hybrid stepping motor－neural position servo system［C］∥Industrial Electronics Society.Denver，USA：IEEE，2001：948－952.

［6］王泮海，徐殿國，史敬灼.基于模糊神經網絡控制的混合式步進電機伺服系統研究［J］.高技術通訊，2004，10（5）：60－63.

［7］Miura T，Taniguchi T.Open－loop control of a stepping motor using oscillation－suppressive exciting sequence tuned by genetic algorithm［J］.IEEE Trans Industry E－lectron，1999，46（6）：1192－1198.

［8］Yang T.Architectures of computational verb controllers：towards a new paradigm of intelligent control［J］.International Journal of Computational Cognition，2005，3（2）：74－101.

［9］Yang T.Simple computational verb PID controllers［J］.International Journal of Computational Cognition，2009，7（1）：61－73.

［10］Zheng X Q，Guo D H.Study on driving control of twophase stepping motor based on mixing mode PWM［J］.Journal of System Simulation，2012，24（2）：456－461.