采用支持向量機的水聲通信信號調制識別方法

江偉華，曹秀嶺，童 峰

（廈門大學 海洋與地球學院，水聲通信與海洋信息技術教育部重點實驗室，福建 廈門361005）

隨著信息獲取和處理需求的不斷提升，對水聲通信信號調制樣式的自動識別研究成為重要的研究課題.目前無線領域常用的通信信號的調制識別方法［1－4］，往往需要較多的調制參數作為先驗知識.由于水聲信道具有復雜的時－空－頻變特性，使得所需的先驗知識在水聲信號調制方式未知的情況下很難得到，因此，非合作水聲通信信號的自動識別極具挑戰性.

調制信號的循環相關特征具有很好的識別能力，Wu等［5］通過循環譜提取水聲信號的特征參數，實驗結果表明該方案可以獲得不錯的識別性能.楊柳等［6］則進行了高階譜的仿真分析，仿真結果表明該算法對不同水聲信道環境有一定的適應性.但循環譜估計和高階譜的計算需要較高的運算量，且遠遠大于相同頻率分辨率的功率譜估計，因此大大限制了這一類調制識別方法的實際推廣應用.

范海波等［7］提出了一種基于譜特征的通信信號調制方式自動識別方法，從信號功率譜、平方譜中提取無需調制參數的特征參數作為特征向量，在較低信噪比下仍具有很好的識別準確率.但是，與無線信道相比，在水聲信道惡劣傳輸條件下無需先驗知識的特征參數往往呈現出嚴重的不穩定性、隨機性，對分類器性能提出了更高的要求.

就分類器而言，Nandi等［1－2］使用統計判決的識別方法，并結合人工神經網絡算法（ANN）來識別和模擬數字信號.但傳統ANN算法經常遇到過學習、欠學習和局部最小化等問題，同時ANN充分訓練所需的大量樣本數據在水聲實際應用中往往無法保證.Vapnik等［8－9］基于結構風險最小化準則提出的支持向量機（SVM）方法不僅可以最小化分類錯誤，還可提高泛化能力，并具有突出的小樣本學習能力.吳丹等［10］提出基于多類別SVM的調制識別方案，這種方法比傳統的ANN算法具有結構簡單、可靠性高、性能好的優勢.SVM分類器已廣泛應用于水聲信號的識別分類中，田杰等［11］將SVM分類器應用于被動水聲目標的識別分類，可以獲得比最近鄰分類器更好的識別效果.

本文基于水聲信號功率譜和平方譜提取無需先驗知識的特征參數，利用SVM設計了一種具備二進制相移鍵控（BPSK）、正交相移鍵控（QPSK）、多進制頻移鍵控（MFSK）等常用水聲通信信號調制方式識別的自動分類器.海上實錄信號的調制識別結果表明，與傳統ANN分類器相比，本文采用的最小二乘支持向量機（LS－SVM）分類器識別率高，且對不同水聲信道具有較好的穩健性.

1 水聲通信信號特征提取

1.1 信號功率譜的形狀特征

信號的功率譜表示了信號功率隨著頻率的變化情況，因此，頻移鍵控信號與非頻移鍵控信號在信號功率譜上有很大的不同，MFSK信號在各調制頻率上會出現明顯的單頻分量，這與相移鍵控（PSK）信號無離散譜線的單峰有著明顯的區別.因此，以信號功率譜的形狀作為特征可以識別出MFSK調制，如文獻［7］中的平坦度指數F，但是計算F值需要預先估計信號的載波頻率.本文考慮在無先驗知識條件下，采用參數R來體現信號功率譜的形狀特征.R參數［12］反映信號功率譜包絡的變化程度，定義如下：

其中u，σ2分別是信號功率譜包絡的均值和方差.由定義式可知，若信號譜平坦，則R值趨于0.若信號存在多個峰，R值隨著譜峰數的減少而增大.本文將R值的u2，σ2作為特征參數集，用來識別MFSK信號.

圖1為對某淺海水聲信道獲取的水聲調制信號進行功率譜分析獲取的信號u2，σ2二維圖.由于MFSK信號功率譜表現為幾條對應于各調頻頻點的離散譜線，其余部分則接近背景噪聲譜，幅度較低；而PSK信號功率譜表現為分布連續的寬帶譜特征.因此在功率譜形狀特征上，MFSK信號功率譜包絡的u2值明顯小于PSK信號功率譜包絡u2值.從圖1可知，參數u2，σ2能夠較好的將信號分為兩類：MFSK、PSK信號.因此，本文將u2，σ2作為功率譜的特征參數進行MFSK和PSK信號的調制識別.

1.2 信號平方譜的離散譜線特征

信號平方譜［13］為信號平方后的功率譜，反映了信號平方后的頻率在功率譜上的表現.信號平方運算會產生零頻分量，所以首先要去掉功率譜的直流成分.BPSK經過平方變換后會在對應2倍載頻位置上出現一條離散譜線，而QPSK信號的平方譜則無離散譜線的單峰.因此，BPSK和QPSK平方譜具有明顯的不同特征，可通過譜峰檢測方法實現對信號的識別.

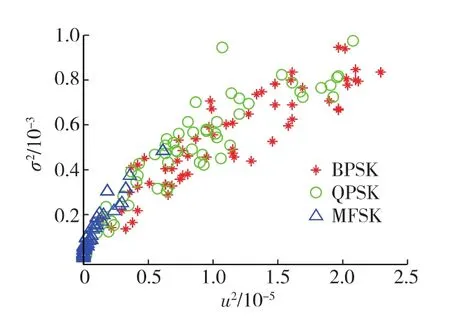
圖1 水聲通信信號u2，σ2參數二維圖Fig.1 Two－dimensional map of u2，σ2 parameter

由于理想的矩形基帶脈沖的沖擊響應拖尾長，占用帶寬大，容易產生碼間干擾，所以在實際水聲通信中，PSK信號調制通常采用脈沖成形技術.為了消除成形濾波器對信號幅度的影響，本文首先通過瞬時幅度對信號進行歸一化.包絡歸一化處理可以消除成形濾波器對調相信號（如PSK）的影響，卻不會影響其調制信息［14］.基于這樣的原理，文獻［15］中通過設定閉值th1，根據大于th1門限值的平方譜譜峰數目N對BPSK和QPSK信號進行類內識別.本文采用參數SN來表征平方譜譜峰.

為了提取平方譜的頻率分量，對平方譜歸一化后，用正交基內積法對平方譜進行滑動窗的擬合處理，得到擬合曲線，然后采用平方譜數據減去擬合曲線得到瞬變譜，并以此作為譜峰判決的依據［16］.定義SN＝瞬變譜中大于設定門限的譜峰數目.本文同時將參數N也作為特征參數，通過提取參數N、SN特征向量可對BPSK和QPSK信號進行調制識別.實現峰值統計如圖2所示.圖3為從某淺海水聲信道獲取的BPSK、QPSK水聲通信信號提取的N、SN參數二維圖.從圖3可知，參數N和SN 可較好的對BPSK和QPSK信號進行區分.本文采用參數N和SN作為區分BPSK和QPSK調制信號的特征參數.

2 SVM分類器設計

2.1 SVM 原理

圖2 平方譜峰值提取流程圖Fig.2 Flow chart of square spectrum peak statistics

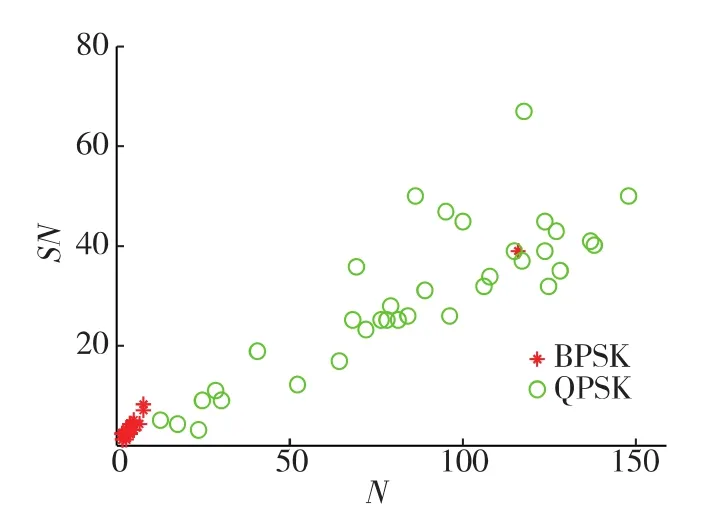
圖3 水聲通信信號N，SN參數的二維圖Fig.3 Two－dimensional map of N，SNparameter

SVM可自動尋找出對分類有較好區分能力的支持向量，由此構造出的分類器可以最大化類與類的間隔，較好地解決了小樣本、非線性、高維數、局部極小點等問題，成為求解模式識別問題的有效工具.

對訓練數據集：

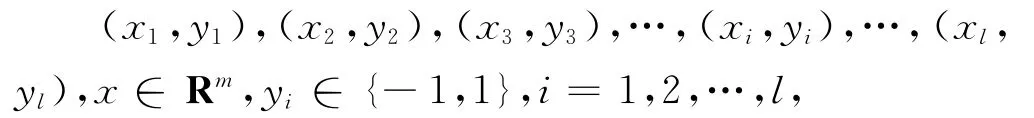
式中，xi和yi分別表示訓練向量和類別標識.可通過非線性變換把線性不可分問題轉化為線性可分問題，并在變換空間求最優分類面.該問題的數學形式為：

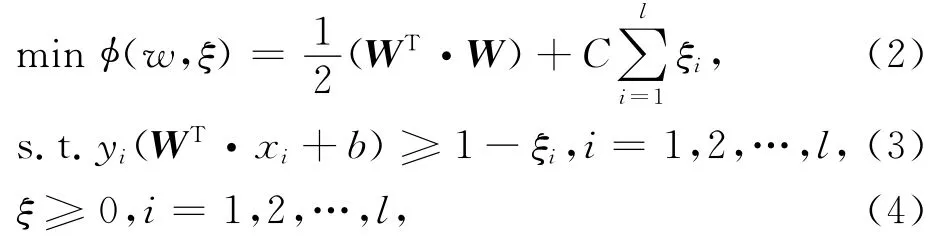
式中，ξi為松弛變量，常數C為懲罰參數，它控制對錯分樣本的懲罰程度.引入核函數可將輸入空間映射到高維的特征空間，求取最優分類超平面.首先對ai求解下列函數的最大值：

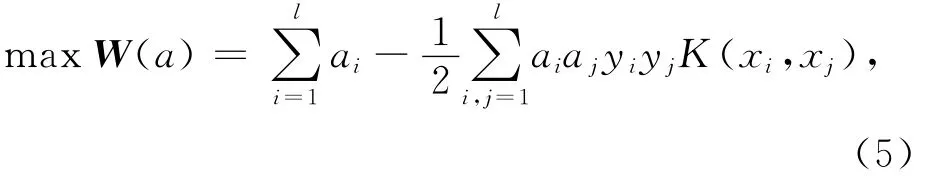
其中ai為Lagrange乘子，K（xi，xj）＝φ（xi）·φ（xj）為核函數.則最優分類函數式相應變為：

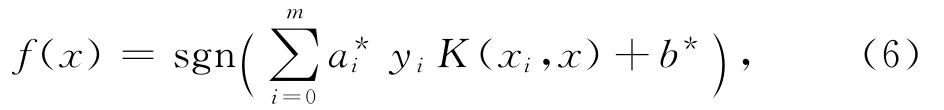
式中，m為支持向量的個數.

2.2 LS－SVM

LS－SVM是SVM的一種擴展，其算法簡練，計算速度快；把SVM中的不等式約束轉化為等式約束；利用LS－SVM提取特征，可有效降低輸入樣本維數、縮減模型運算時間，還具有突出的非線性回歸能力.

LS－SVM通過解線性方程方法代替解凸二次規劃方法，則優化問題變為：

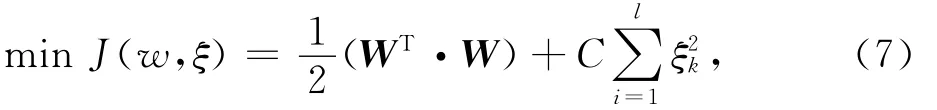
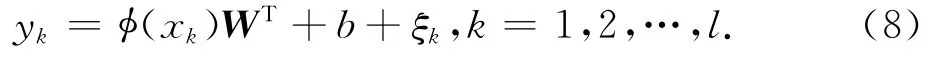
該線性方程可由最小二乘方法求解，LS－SVM由此而得名，且比標準SVM具有更快的訓練速度.

上述SVM只能區分兩類模式的分類問題，而本文所進行的水聲通信信號調制識別涉及3種調制信號，屬于典型的多類分類問題.本文采用最小輸出編碼（code＿MOC）的方法來解決多類分類問題.

3 水聲通信信號調制識別實驗

3.1 調制識別實驗設置

為驗證本文水聲調制識別方案的有效性，采用廈門、青島周邊海域4個不同水聲信道（分別以信道1、2、3、4表示）獲取的水聲通信實驗信號數據進行調制識別實驗.表1給出了4個不同水域實驗信道的具體參數，圖4給出了4個實驗信道的沖激響應，從圖4中可以看出，信道2、3比信道1、4具有較為明顯的多徑，4個實驗信道具有不同類型的水聲信道特性.表1中同時給出了表征信道時變的多普勒頻偏參數，可以看出4個實驗信道均帶有一定的多普勒，其中信道3多普勒為2.0Hz，稍高于其他3個實驗信道.

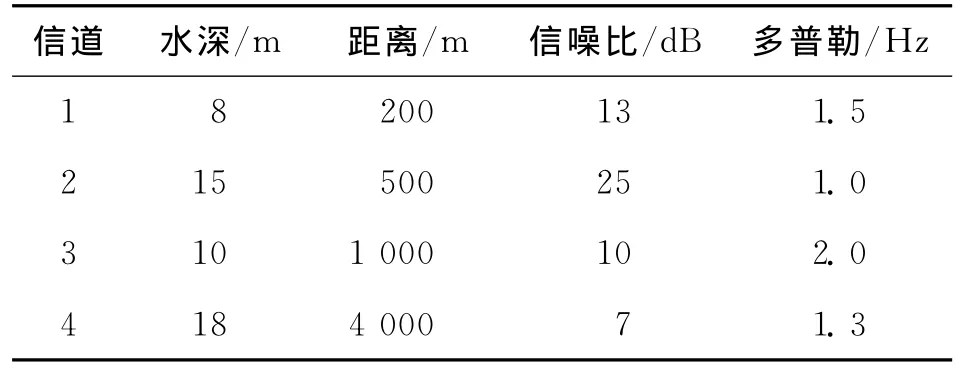
表1 實驗信道參數Tab.1 The parameters of four channels

從4個不同實驗信道獲取的720個水聲通信實驗信號具有以下3類調制類型：BPSK、QPSK、MFSK.其中：MFSK（包括2FSK，4FSK，8FSK）信號268個，QPSK信號249個，BPSK信號203個.信號樣本的采樣率96kHz，16bit量化.表2給出了水聲通信信號數據樣本中各種調制信號的調制參數.

海上實驗系統包括了信號發射和接收部分，發射部分包括調制信號產生、功率放大，最后通過換能器發射信號；接收部分包括接收換能器接收信號后經前置放大、帶通濾波預處理后通過模擬數字采集卡轉換為數字信號送入計算機中進行離線處理.通過對采集到的水聲通信信號進行功率譜、平方譜特征提取，提取功率譜特征參數u2，σ2以及平方譜離散譜峰參數N和SN構成4維特征向量，進行調制識別實驗.

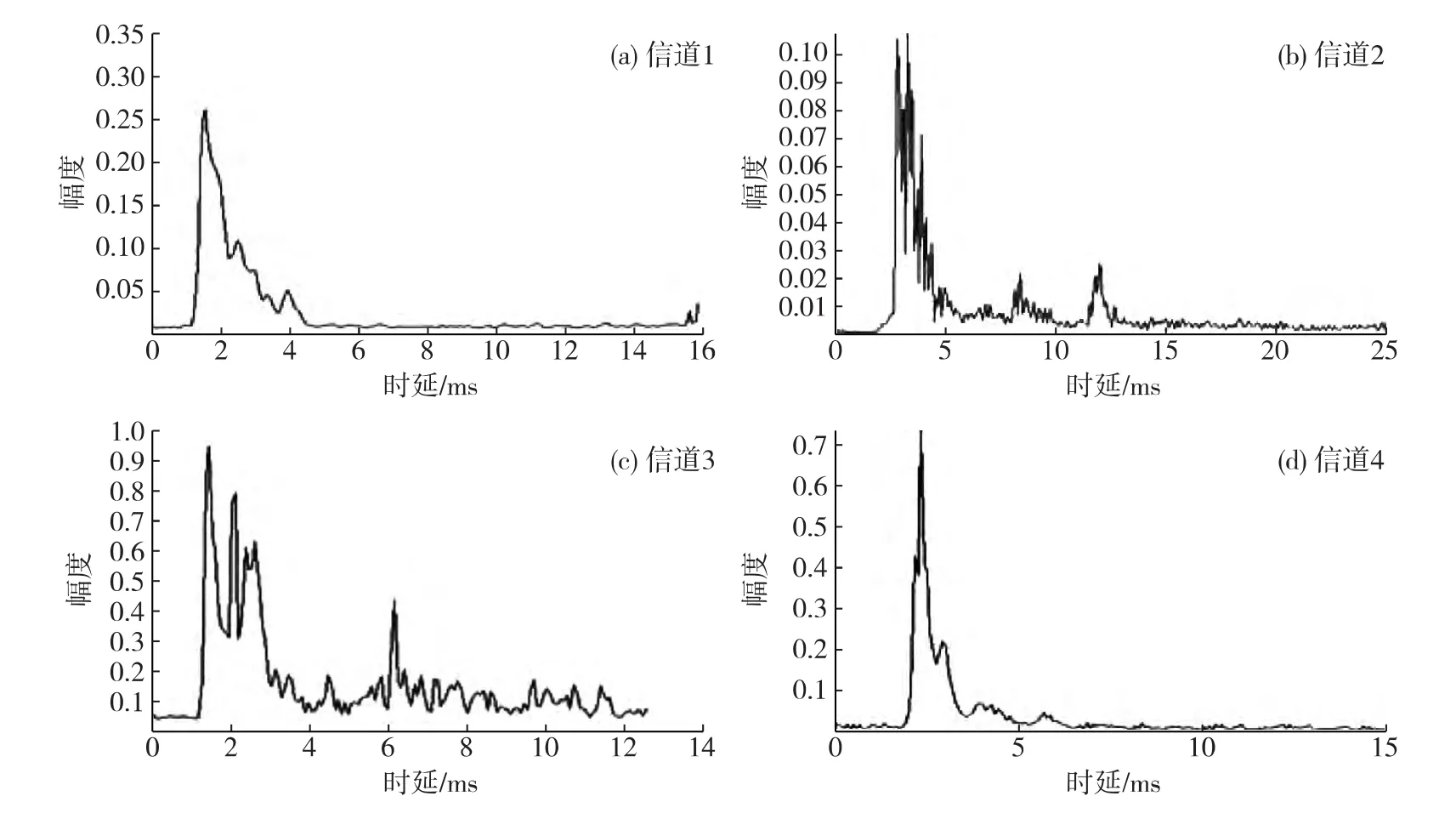
圖4 實驗信道沖激響應Fig.4 The impulse responses of the experimental channels

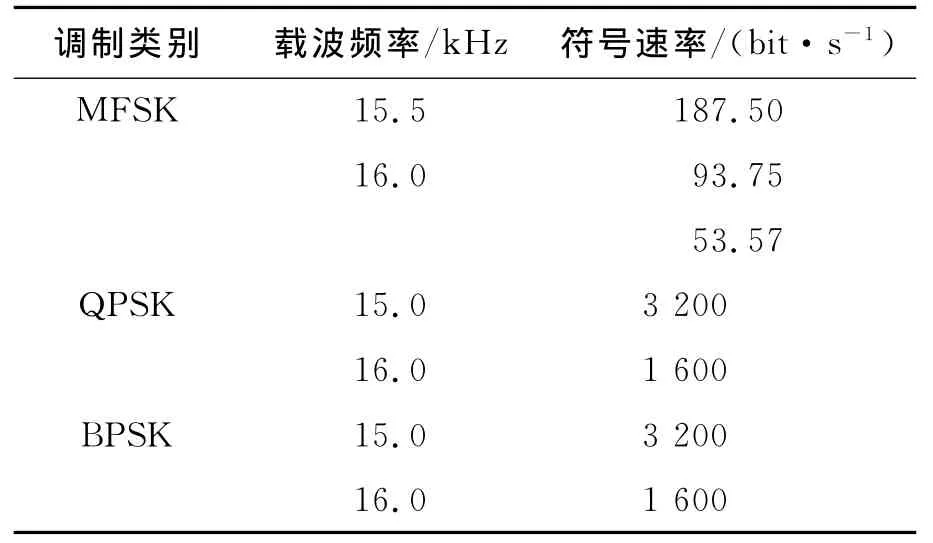
表2 水聲通信信號調制參數Tab.2 Modulation parameter of signal

3.2 分類器設計

本文設計了如圖5所示基于LS－SVM的分類器，將提取的水聲通信信號4維特征參數作為特征向量，利用SVM把特征向量映射到高維空間中，并構建最優分類面對信號BPSK、QPSK和MFSK進行調制方式的自動識別.具體的識別步驟為：

1）從水聲通信信號中提取4個特征參數構成特征向量作為LS－SVM分類器輸入；2）為SVM選擇核函數，本文的識別實驗中選用了徑向核函數.徑向核函數可以將樣本非線性地規劃到更高維的空間中，從而解決類標簽和屬性間非線性的關系問題；3）使用交叉驗證和網格搜索的方法找到最佳參數.選取正則參數gam為13，內核函數的參數sig2為2；4）用訓練樣本對LS－SVM分類器進行訓練，設定訓練迭代的終止條件為訓練誤差小于0.001，完成訓練后對測試樣本進行調制識別測試.

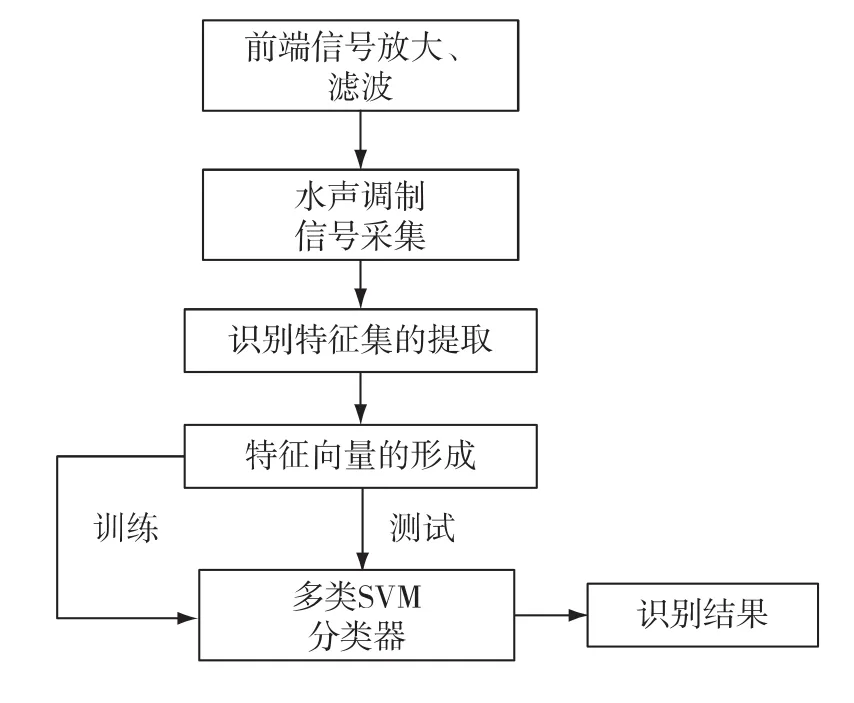
圖5 調制識別系統示意圖Fig.5 Flow chart of modulation recognition system

3.3 實驗結果與分析

本文采用SVM分類器與傳統ANN分類器進行海上通信信號調制識別性能對比，其中：ANN分類器采用3層誤差逆傳播，ANN網絡隱層節點數為10，設定訓練迭代的終止條件為訓練誤差小于0.001；SVM分類器參數設置如3.2節所述.

從總樣本庫中分別隨機選取T個MFSK信號，T個BPSK信號，T個QPSK信號作為訓練集，其余樣本作為測試集.表3給出了ANN分類器在訓練樣本數T＝50和100條件下的調制識別結果.從表3可知：當T＝50時，調制信號的正確識別率較低，除了MFSK外，BPSK和QPSK的調制方式的識別率都小于90%；當T＝100時，正確識別率得到了明顯的改善，尤其是QPSK信號的識別率提高了3.45個百分點.這說明樣本數在很大程度上制約著ANN的性能.

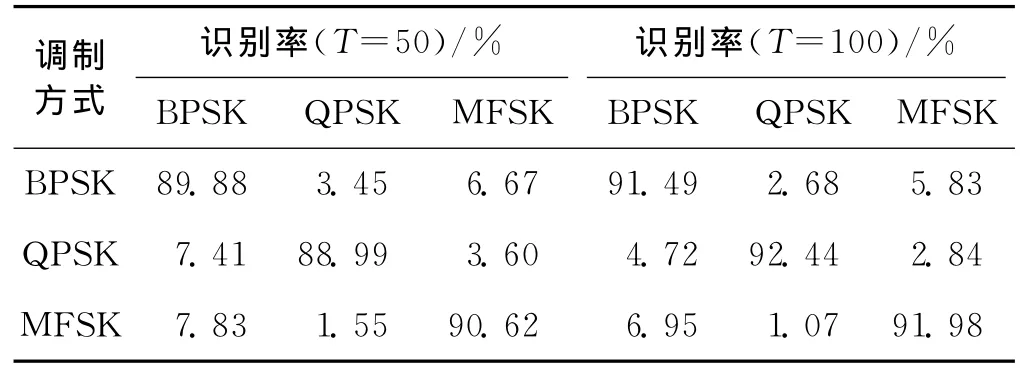
表3 ANN分類器的識別率Tab.3 The recognition rate of ANN modulation classifier

表4給出了LS－SVM分類器在訓練樣本數T＝50和100條件下的識別結果.可以看出，隨著T的變化，正確識別率的改變程度與表3相比不是那么顯著.在T＝50時，信號調制方式的識別率都在91%以上，在T＝100時，信號調制方式的識別率都在92%以上.結果表明：LS－SVM的調制識別性能優于ANN.

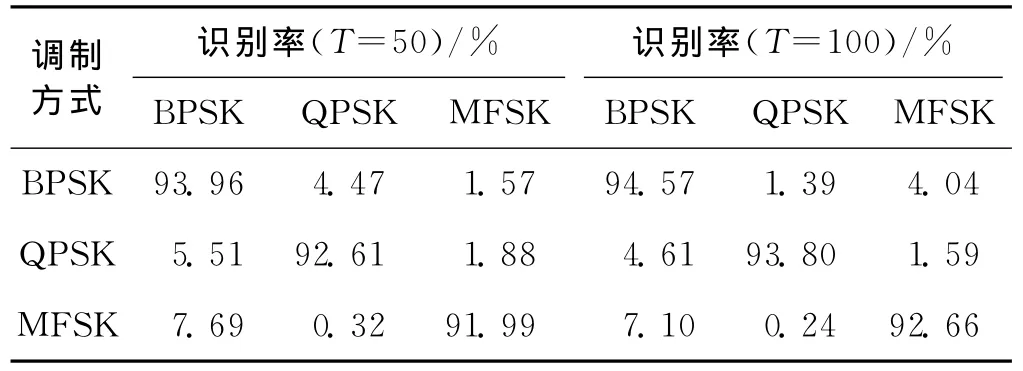
表4 LS－SVM分類器的識別率Tab.4 The recognition rate of LS－SVM modulation classifier

考慮到實際水聲信號處理應用中獲取的訓練樣本有限，本文比較了兩種分類器的小樣本學習性能.圖6給出了訓練樣本數T從10到100時兩種分類器的識別性能，可以看出隨著樣本數的增加，特征值更加接近理想值，SVM分類器和ANN分類器識別性能都顯著提高.而ANN在樣本數較少時，神經網絡結構構造不充分，因此性能較差；LS－SVM基于結構風險最小化的原理可充分利用特征參數集信息，所以在樣本數較少時LS－SVM識別率明顯高于ANN.

水聲信道隨機、復雜的時－頻擴展特性引入的信號畸變是影響水聲通信信號調制識別性能的重要影響因素.為了評估本文方案與ANN分類器對于不同水聲信道的穩健性，本文比較了訓練集和測試集均從同類型水聲信道樣本隨機選取，以及訓練集和測試集分別采用不同類型水聲信道樣本時對QPSK信號的調制識別性能.表5給出了訓練樣本數T＝30時兩種情況下的QPSK信號識別結果，從表5可看出：ANN分類器在訓練集和測試集分別采用不同信道類型時其調制正確識別率比訓練集和測試集均從同類型信道隨機選取降低了16.75個百分點；而在同樣兩種條件下，對應的LS－SVM分類器識別率只降低了約5個百分點.這表明本文LS－SVM分類器對于不同水聲信道的穩健性明顯優于ANN分類器.

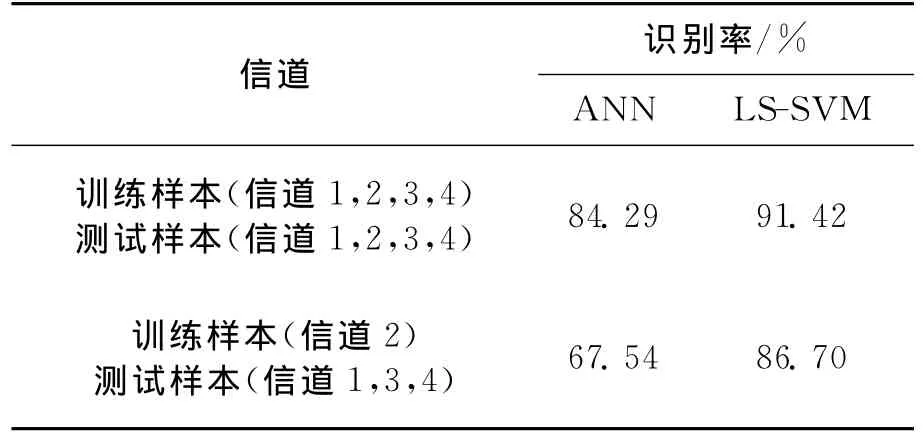
表5 采用不同類型訓練／測試信道時QPSK信號識別率Tab.5 The recognition rate of QPSK signal under different training／testing channel type

4 結 論

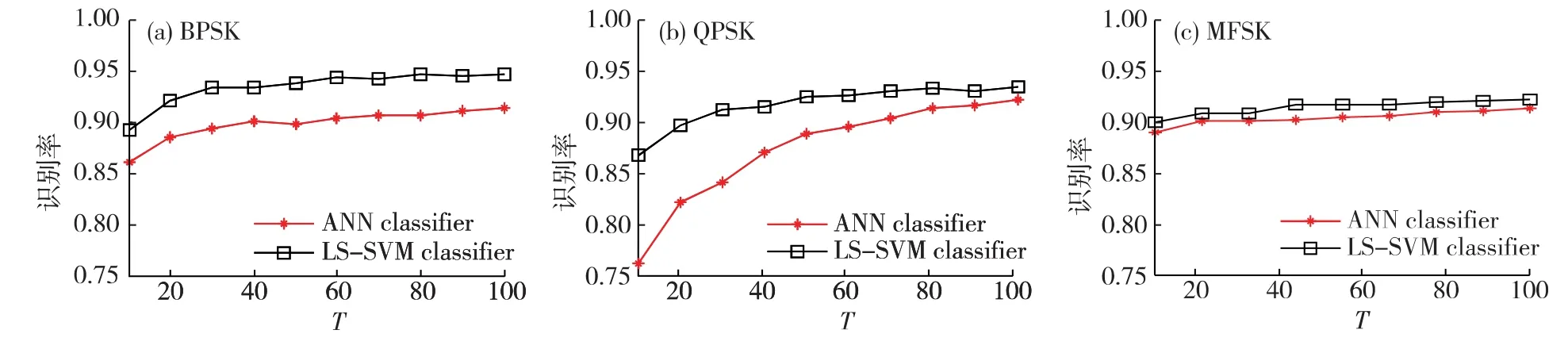
圖6 不同訓練樣本條件下水聲調制信號識別率曲線Fig.6 The recognition rate curve of underwater acoustic modulation signal under different number of training set

針對非合作水聲通信信號調制識別，本文提出了一種基于SVM的水聲通信信號調制識別方法，該方法使用功率譜、平方譜中提取的4個特征參數構成無需先驗知識的特征向量，利用SVM分類器對BPSK、QPSK和MFSK 3種常見水聲通信調制信號進行調制識別測試.實驗結果初步表明，本文識別方法的識別性能、小樣本學習能力及對不同水聲信道穩健性均優于傳統ANN分類器.

［1］Nandi A K，Azzouz E E.Automatic analogue modulation recognition［J］.Signal，Processing，1995，46（2）：211－222.

［2］Nandi A K，Azzouz E E.Algorithms for automatic modulation recognition of communication signals［J］.IEEE Trans Commun，1998，46（4）：431－436.

［3］Swami A，Sadler B M.Hierarchical digital modulation classification using cumulates［J］.IEEE Trans Commun，2000，48（3）：416－429.

［4］Gardner W A，Spooner C M.Cyclic－spectral analysis for signal detection and modulation recognition［C］∥Military Comunications Conference.San Diego，CA，USA：IEEE，1988：419－424.

［5］Wu Z，Yang T C，Liu Z，et al.Modulation detection of underwater acoustic communication signals through cyclostationary analysis［C］∥ Military Communications Conference.Orlando：IEEE，2012：1－6.

［6］楊柳，趙曉群，徐靜云.水聲信號的調制方式識別［J］.燕山大學學報，2014，38（2）：156－162.

［7］范海波，楊志俊，曹志剛.衛星通信常用調制方式的自動識別［J］.通信學報，2004，25（1）：140－149.

［8］Vapnik V N.Statistical learning theory［M］.New York：John Wiley and Sons，1998：81－85.

［9］Cortes C，Vapnik V N.Support vector networks［J］.Machine Learning，1995，20：144－152.

［10］吳丹，顧學邁.一種新的基于支持向量機的自動調制識別方案［J］.南京理工大學學報：自然科學版，2006，30（5）：569－572.

［11］田杰，張春華，劉維，等.基于倒譜分析的被動水聲目標分類 ［J］.系 統 工 程 與 電 子 技 術，2005，27（10）：1708－1710.

［12］Chan Y T，Gadboi L G.Identification of the modulation type of a signal［J］.Signal Processing，1989，16（2）：149－154.

［13］Dubuc C，Boudreau D.An automatic modulation recognition algorithm for spectrum monitoring applications［C］∥IEEE International Conference on Communications（ICC′99）.Vancouver，Canada：IEEE，1999：732－736.

［14］黃如容.數字信號調制方式識別方法的設計與實現［D］.成都：西南交通大學，2012：8－10.

［15］劉芳.基帶通信信號的參數估計、調制識別及解調［D］.濟南：山東大學，2007：40.

［16］童峰，陸佶人，方世良.水聲目標識別中一種軸頻提取方法［J］.聲學學報，2004，29（5）：398－402.