基于能量函數(shù)的電網(wǎng)暫態(tài)穩(wěn)定性離線量化指標研究

劉群英，劉起方，劉 登，廖永鋒（.電子科技大學自動化工程學院 成都 67；.中國國電集團四川公司阿水電力開發(fā)有限公司 成都 600；.四川省電力公司資陽公司 四川 資陽 646）

·自動化技術·

基于能量函數(shù)的電網(wǎng)暫態(tài)穩(wěn)定性離線量化指標研究

劉群英1，劉起方2，劉 登3，廖永鋒1
（1.電子科技大學自動化工程學院 成都 611731；2.中國國電集團四川公司阿水電力開發(fā)有限公司 成都 610021；3.四川省電力公司資陽公司 四川 資陽 641316）

基于李亞普羅夫直接法的能量裕度一直被認為是評價電力系統(tǒng)暫態(tài)穩(wěn)定性的一個重要指標，而能量裕度一直是在線應用關注的重點。該文首先結合經(jīng)典的電力系統(tǒng)轉子運動方程，構建了暫態(tài)能量函數(shù)模型，然后分析了穩(wěn)定域基本特征及其與電力系統(tǒng)勢能邊界的對應關系，并采用二次擾動與基于勢能邊界特性的插值法相結合的思路獲取勢能最大值，最后基于勢能最大值構建了電網(wǎng)暫態(tài)穩(wěn)定性量化指標。通過在三機系統(tǒng)和IEEE-30母線系統(tǒng)的系列仿真結果及其與CUEP法的對比，驗證了該方法能夠提高計算速度和計算精度，可用于電力系統(tǒng)暫態(tài)穩(wěn)定性的離線評估。

能量裕度；穩(wěn)定域；二次擾動；暫態(tài)穩(wěn)定性

隨著電力系統(tǒng)暫態(tài)穩(wěn)定性評估要求的提高，電網(wǎng)暫態(tài)穩(wěn)定性評估理論與方法的研究，除了要給出系統(tǒng)暫態(tài)穩(wěn)定性的定性結論外，還需要對穩(wěn)定程度甚至發(fā)展趨勢進行量化分析。從近年國內(nèi)外該方向的研究發(fā)展過程來看，主要是基于量化指標模型的構建評估其暫態(tài)穩(wěn)定性程度和發(fā)展趨勢。而關于量化指標模型的構建理論和方法，迄今為止，也取得了不少的成果，其研究思路主要集中在兩類：不確定性分析方法和確定性分析方法。

不確定性分析方法基于隨機理論［1-2］和概率分布［3-4］。確定性分析方法主要有基于支持向量機的方法［5-6］、回歸法［7］、用于搜索多擺暫態(tài)穩(wěn)定約束的靈敏性法［8］、解軌跡跟蹤法［9］、修正的直流潮流法［10］和能量函數(shù)法［11-15］。作為確定性分析法重要分支的直接法，其研究在20世紀60－90年代期間最為活躍，所取得的成果為其后來在暫態(tài)穩(wěn)定性中的實際應用奠定了堅實理論基礎。直接法及其基礎上發(fā)展的能量函數(shù)法依然是暫態(tài)穩(wěn)定性研究所依賴的主要方法。文獻［11-14］基于能量函數(shù)，從不同的角度進行了暫態(tài)穩(wěn)定性的機理及評估指標研究。文獻［11］構造了基于聯(lián)絡線的能量函數(shù)，并將能量分解為振蕩分量和準穩(wěn)態(tài)分量，從而對多重擾動引起的系統(tǒng)低頻振蕩進行分析。文獻［12］利用轉子加速度方程得到等效單機無窮大系統(tǒng)，以此構造等效暫態(tài)能量函數(shù)，有利于簡化運算。文獻［13］針對支路勢能邊界面方法的不足，推導了電力系統(tǒng)暫態(tài)穩(wěn)定及臨界割集識別判據(jù)。文獻［14］基于勢能變化，使用了臨界發(fā)電機母線對的相角差監(jiān)測暫態(tài)穩(wěn)定裕度。文獻［15］基于Lyapunov直接法，應用了正定多項式、半正定程序以及平方解耦的和處理具有多項式向量場的系統(tǒng)暫態(tài)穩(wěn)定性。

為了提高暫態(tài)穩(wěn)定性計算效率，并行計算的思路近年被提出。文獻［16］將s級2s階的辛龍格-庫塔-奈斯通法用于經(jīng)典模型的電力系統(tǒng)暫態(tài)穩(wěn)定性計算，利用矩陣分裂技巧以及矩陣求逆運算的松弛法，推導了暫態(tài)穩(wěn)定性并行計算法。文獻［17］通過全牛頓迭代、基于稀疏矩陣的線性求解器求解并行結構的多圖像處理單元，加速大規(guī)模電力系統(tǒng)暫態(tài)仿真計算。

以上研究為進一步研究電力系統(tǒng)暫態(tài)穩(wěn)定性的計算速度和精確性的提高方法提供了理論支撐。然而，在電力系統(tǒng)發(fā)展的新形勢下，現(xiàn)有的電力系統(tǒng)暫態(tài)穩(wěn)定性的評估，因其在結合實際系統(tǒng)物理特性方面的不足而受到局限，更快速、更簡便的評估方法依然是電力運行人員關注的重點。

本文基于經(jīng)典的發(fā)電機轉子運動方程和功率平衡方程，構建了暫態(tài)能量函數(shù)模型；基于電力系統(tǒng)動能和勢能的轉換關系及穩(wěn)定域基本特征，采用二次擾動法與插值法相結合來獲取勢能最大值；基于勢能最大值構建了電網(wǎng)暫態(tài)穩(wěn)定性評估指標。在三機系統(tǒng)和IEEE-30母線系統(tǒng)中的仿真結果及其與CUEP方法的對比分析，驗證了方法的有效性和可行性。

1 能量函數(shù)模型構建

單機無窮大系統(tǒng)的接線如圖1所示。

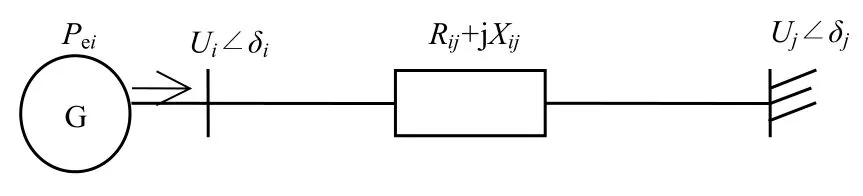
圖1 單機無窮大系統(tǒng)

系統(tǒng)受到擾動時，發(fā)電機轉子運動方程為：

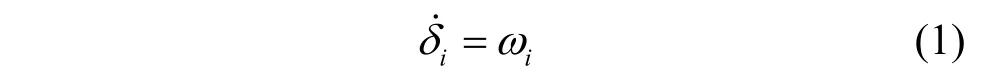
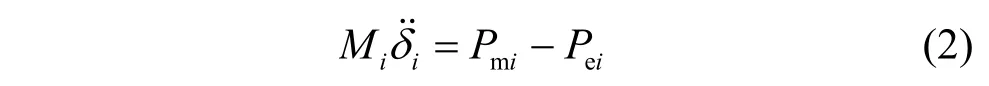
式中，δi、ωi分別為發(fā)電機的轉子角和轉速；Pmi、Pei分別為發(fā)電機的機械功率和電磁功率；Mi為慣性時間常數(shù)。式（2）中，令：

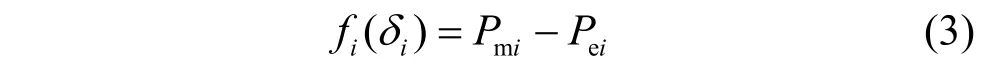
根據(jù)李亞普羅夫直接法，由式（1）、式（3）可得發(fā)電機的能量函數(shù)表達式為：

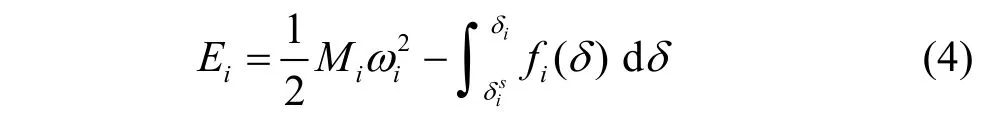
設：

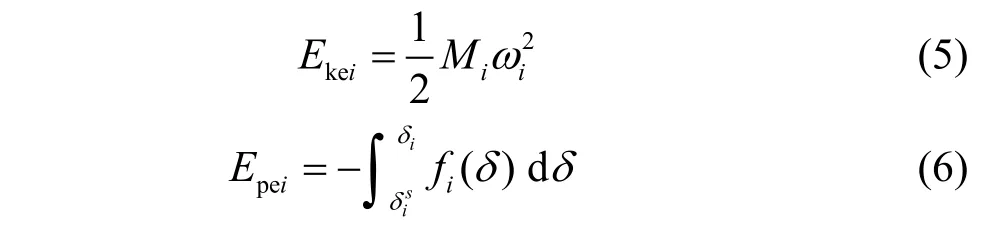
在多機系統(tǒng)中則是動能和勢能的迭加，有：

式（4）和式（7）中第1項代表系統(tǒng)的動能，第2項代表系統(tǒng)的勢能。本文的重點在于勢能最大值的求取方法的研究，因此采用了經(jīng)典的能量函數(shù)表達式，以求得到一般性的結論，故式（4）和式（7）沒有更加詳細地展示有功負荷、無功負荷以及電壓幅值等系統(tǒng)運行參數(shù)在內(nèi)的系統(tǒng)信息。

故障后的穩(wěn)定平衡點（δs，ωs）在該點處有Etot（δs，ωs）=0。上述能量函數(shù)對時間的導數(shù)為：

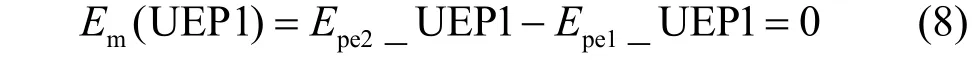
在實際系統(tǒng)中存在阻尼，即：、

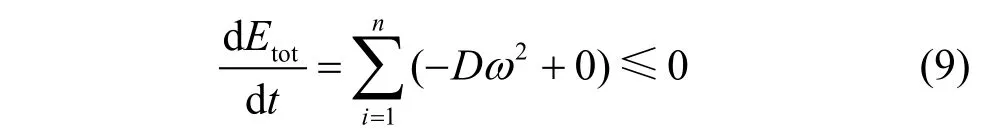
式中，D為阻尼常數(shù)。式（9）表明式（4）在實際中滿足李亞普諾夫直接法的條件，可用于分析電力系統(tǒng)穩(wěn)定性。式（4）和式（7）的第2項都存在路徑依賴問題，采用梯形法來近似計算，對結果的精確性影響不大。

2 基于二次擾動的暫態(tài)穩(wěn)定性離線量化指標構建

在保證一次擾動和二次擾動將回到同一個穩(wěn)定平衡點（SEP）并且二次擾動軌跡是大范圍漸進穩(wěn)定的前提下，二次擾動會盡可能近地通過穩(wěn)定邊界的不穩(wěn)定平衡點（unstable equilibrium point，UEP），但依然在前述的穩(wěn)定平衡點的吸引域內(nèi)。基于這樣的結論，一次擾動屬于小擾動，采用負荷的小幅度等量增加，二次擾動則需施加大擾動，采用三相短路故障。利用這樣的兩次擾動模式，可以得到如圖2所示的仿真結果。

在圖2中，穩(wěn)定區(qū)域邊界上的兩個不穩(wěn)定平衡點分別為UEP1和UEP2，一次擾動和二次擾動軌跡分別經(jīng)過或者接近這兩個不穩(wěn)定平衡點，并且對應這兩個不穩(wěn)定平衡點時將分別出現(xiàn)勢能極值Epe1_UEP1、Epe2_UEP1和Epe1_UEP2、Epe2_UEP2。這里的能量裕度取一次擾動和二次擾動經(jīng)過或者接近同一不穩(wěn)定平衡點時的勢能極值差作為能量裕度，表達式為：

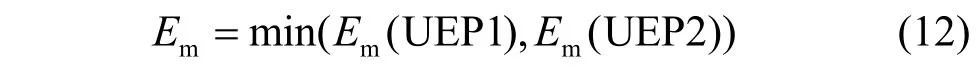
式中，Em（UEP1）和Em（UEP2）分別為對應不穩(wěn)定平衡點UEP1和UEP2的能量裕度。由于仿真或者計算精度的影響，式（10）和式（11）中的結果會存在一定的差距，從保證安全性的角度考慮，將取兩者中的極小值，最后的能量裕度為：式（12）衡量的是當前系統(tǒng)的運行點距離穩(wěn)定邊界的距離，該值越大，說明系統(tǒng)越穩(wěn)定。當Em=0時，系統(tǒng)已經(jīng)瀕臨失穩(wěn)的臨界狀態(tài)。在系統(tǒng)暫態(tài)過程中，系統(tǒng)的穩(wěn)定性發(fā)展趨勢與故障時注入系統(tǒng)的動能有關，注入系統(tǒng)的動能太多，導致系統(tǒng)當前的網(wǎng)架結構不能完全吸納，則系統(tǒng)容易失穩(wěn)。

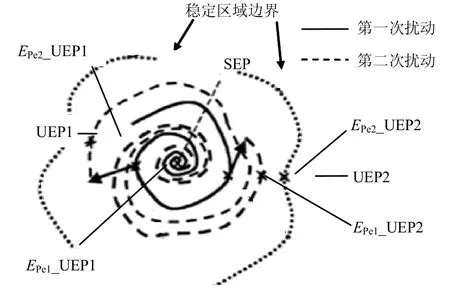
圖2 基于二次擾動的能量裕度計算

3 二次擾動法的具體實現(xiàn)

3.1 二次擾動法的基本原理

根據(jù)現(xiàn)有的文獻，求一個系統(tǒng)完整的穩(wěn)定邊界是不必要的，要求系統(tǒng)的穩(wěn)定裕度，只需要求得某狀態(tài)下運動軌跡對應的CUEP（controlling unstable equilibrium point），再根據(jù)CUEP求得對應的勢能極限Epe_UEP，以此判別該運動軌跡是否穿越穩(wěn)定邊界。

由于CUEP的求取需要較長的計算時間，在求取Epe_UEP時，將結合二次擾動法，以避免求取CUEP，節(jié)約計算時間。二次擾動法［18］的具體實現(xiàn)過程如圖3所示。圖中，時段0～t_start是一次擾動持續(xù)時段，在t_start時刻，對應系統(tǒng)動能最小點Eke（t_start），在t_start＋時刻，對系統(tǒng)第二次施加一個足夠大的擾動，令系統(tǒng)不穩(wěn)定，系統(tǒng)的動能增加，動能軌跡經(jīng)過第二次動能最大時刻為t_clear，此時為故障極限切除時間，對應的動能為Eke（t_clear）；系統(tǒng)完全恢復穩(wěn)定，對應時刻為ts2，對應的動能為Eke（ts2），勢能為Epe（ts2）。

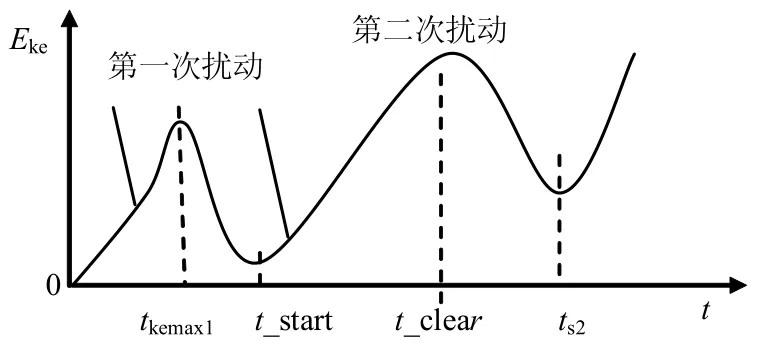
圖3 動能軌跡曲線

勢能極限Epe_UEP對應位于勢能邊界上的不穩(wěn)定平衡點對應的勢能值，即動能全部轉化后的勢能最大值。傳統(tǒng)的CUEP法，計算量很大，為了減少計算量，在計算Epe_UEP時采用插值法獲取最終結果。

3.2 基于插值法的最大勢能值計算

穩(wěn)定邊界上的勢能極限值實際是對應UEP的最大勢能值，因此，在該點處勢能隨時間的變化率為0。如果能得到該點附近任意兩點的勢能變化率及對應的時間，則根據(jù)插值法，可以計算得到對應該點的時間，再根據(jù)該點的時間反推回去計算得到該點的勢能值，即為要求取的最大勢能值。

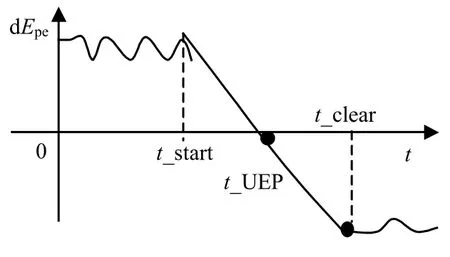
圖4 插值法求勢能極限值

在圖4中，橫坐標代表暫態(tài)過程，縱坐標代表勢能在暫態(tài)過程中的變化量。在式（6）中，由于δi是時間的函數(shù)，因此，在時間t_start和t_clear時刻的勢能變化量dEpe（t_start）和dEpe（t_clear），可以根據(jù)時間t_start和t_clear臨界時刻前后的勢能計算得到。而在t_UEP時刻對應勢能邊界，為勢能極值，其變化量為0，利用插值法，可得：

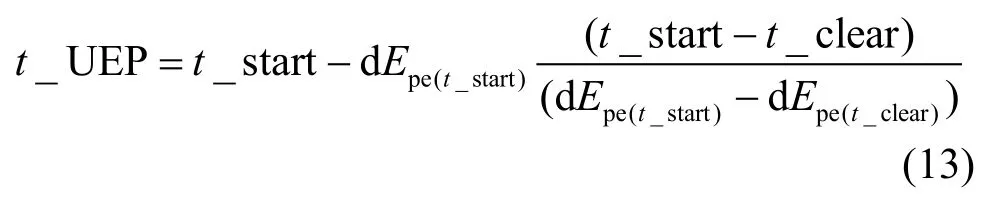
該思路的依據(jù)是PEBS對應勢能最大值，且勢能在PEBS穿越點的變化率為0。在式（13）中，t_start為第一次擾動發(fā)生的時刻，t_clear為二次擾動發(fā)生后動能最大時刻，可根據(jù)動能仿真曲線得到。dEpe（t_start）和dEpe（t_clear）已知，因此，可以計算得到t_UEP，然后根據(jù)式（11）得到對應該時刻的Epe（t_UEP）為：

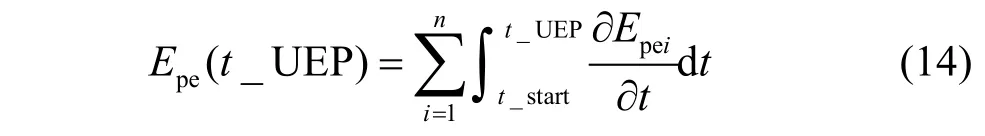
式（14）的計算一方面避免了計算ts2時刻的動能和勢能，另一方面也避免了直接求解CUEP或者勢能邊界逸出點，一定程度上減少了計算量。缺點是需要保存t_start時刻的運行狀態(tài)，并離線實施二次擾動，這在一定程度上增加了計算時間。

4 實例驗證

4.1 三機系統(tǒng)仿真分析

三機系統(tǒng)的接線如圖5所示。

圖5 三機系統(tǒng)接線圖

圖5中G1、G2和G3為發(fā)電機，G3為參考發(fā)電機，具有較大的慣性，帶有快速響應控制器，G1和G2都帶有快速勵磁控制系統(tǒng)。在每臺發(fā)電機母線處都存在負荷，Load1=12.06+j2.14MVA，Load2=8.23+j4.26MVA，Load3=5.20+j5.10MVA。x12、x23和x13為線路電抗，且x12=x23=x13=0.30。

1）系統(tǒng)軌跡變化分析。

一次擾動為三相短路故障，發(fā)生在支路1-2的中點，系統(tǒng)穩(wěn)定后的第50s時刻，持續(xù)0.5s清除；二次擾動發(fā)生在70s時刻，持續(xù)0.5s清除。圖6為從啟動到穩(wěn)定的過程（0～40s）中的系統(tǒng)軌跡變化曲線。圖6a中的Sep1、Sep2和Sep3分別是發(fā)電機1、2和3的初始穩(wěn)定平衡點，分別對應坐標（0.99，54.37°）、（0.99，55.78°）和（0.99，42.13°）。從圖6a可以看出，3臺發(fā)電機在啟動以后都以很快的速度到達了穩(wěn)定平衡點。

圖6b表示一次擾動發(fā)生在50s時刻，從故障發(fā)生到系統(tǒng)達到穩(wěn)定平衡點（50～60s）的軌跡。圖6b中的Sep1、Sep2和Sep3分別是發(fā)電機1、2和3經(jīng)歷一次擾動后的穩(wěn)定平衡點，分別對應坐標（0.978，54.67°）、（0.978，55.90°）和（0.978，42.15°）。與圖6a中的穩(wěn)定平衡點相比，無論是平衡點的角速度還是轉子角，都有極小的移動，說明三相短路故障對該系統(tǒng)的整體暫態(tài)穩(wěn)定性有較大影響，導致發(fā)電機不能回到初始穩(wěn)定點。

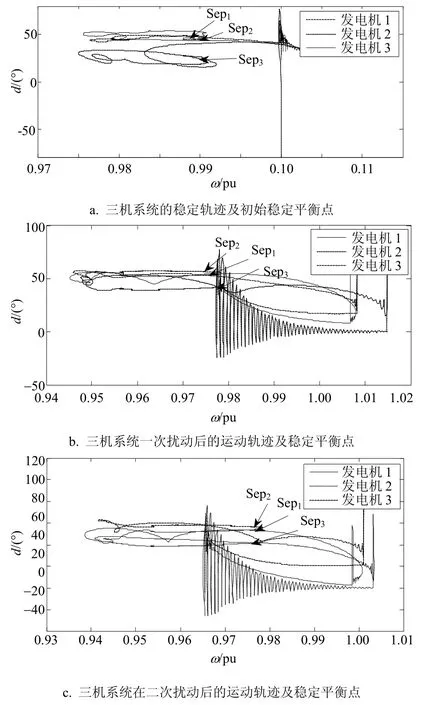
圖6 系統(tǒng)軌跡變化曲線

圖6c表示二次擾動（三相短路故障，發(fā)生在支路1-2的中點）發(fā)生在70s時刻，從擾動發(fā)生到擾動清除清除并最終穩(wěn)定的過程（70～150s）中的軌跡變化曲線。圖中SEP1、SEP2和SEP3分別是發(fā)電機1、2和3經(jīng)歷二次擾動后的穩(wěn)定平衡點，分別對應坐標（0.978，54.66°）、（0.978，55.88°）和（0.978，42.14°）。相比較于圖6b，3臺發(fā)電機的平衡點位置幾乎沒有移動，僅從平衡點的變化來看，第二次三相短路故障沒有對系統(tǒng)的穩(wěn)定性造成太大的影響。

2）在故障過程中的動能和勢能變化的計算。

根據(jù)兩次擾動后的運動軌跡和推導的動能和勢能計算模型，可以得到兩次擾動過程中系統(tǒng)的動能和勢能變化曲線如圖7和圖8所示。

在系統(tǒng)中，系統(tǒng)任何時刻動能和勢能是守恒的，從圖7和圖8所示的動能和勢能變化曲線也驗證了這一動能和勢能的守恒性。另外，對于系統(tǒng)而言，兩次擾動相當于對系統(tǒng)注入了兩次動能，這兩次注入的動能在忽略系統(tǒng)其他動能消耗的情況下最終將轉化為不同形式的勢能存在于系統(tǒng)中。因此，在圖8中，第一次擾動注入的動能全部轉化為勢能后，在達到穩(wěn)定狀態(tài)后不再變化，在第二次擾動再次注入動能后，勢能階梯型爬升，勢能隨著時間的變化呈現(xiàn)迭加的態(tài)勢，一旦動能全部轉化為勢能以后，系統(tǒng)的勢能將維持不變。

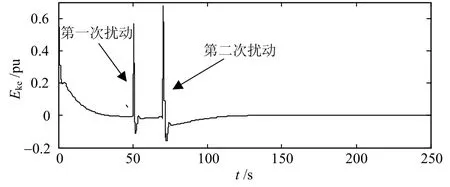
圖7 三機系統(tǒng)從啟動到經(jīng)歷兩次擾動的動能變化曲線

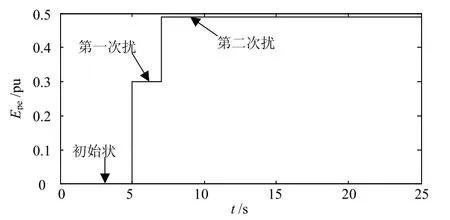
圖8 三機系統(tǒng)對應不同擾動的勢能變化

3）能量裕度計算結果。

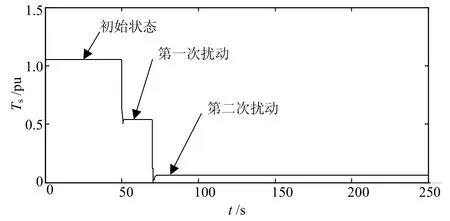
圖9 三機系統(tǒng)從啟動到經(jīng)歷兩次擾動的能量裕度變化曲線

圖9展示了系統(tǒng)在初態(tài)以及經(jīng)受了兩次擾動后的能量裕度的變化情況。系統(tǒng)初始狀態(tài)時的能量裕度在1附近，而經(jīng)歷了一次擾動以后，能量裕度下降到0.5左右，在經(jīng)歷了二次擾動后，則下降到0.1左右，此時系統(tǒng)的能量裕度非常小，系統(tǒng)已經(jīng)開始脆弱化，如果再有一次擾動，系統(tǒng)將瀕臨失穩(wěn)。值得提出的是，在系統(tǒng)軌跡變化分析中考察穩(wěn)定平衡點時，第一次擾動和第二次擾動后的穩(wěn)定平衡點幾乎保持一致，相比較根據(jù)能量裕度的計算得出的暫態(tài)穩(wěn)定性判斷結果，說明單純通過判斷穩(wěn)定運行點是否移動來給出系統(tǒng)穩(wěn)定性是否改變的思想可能導致錯誤的暫態(tài)穩(wěn)定性判斷。

4.2 IEEE-30母線系統(tǒng)的仿真分析

IEEE-30母線系統(tǒng)共有6臺發(fā)電機，30條母線，41條支路，4臺有載調(diào)壓變壓器，系統(tǒng)的接線如圖10所示。

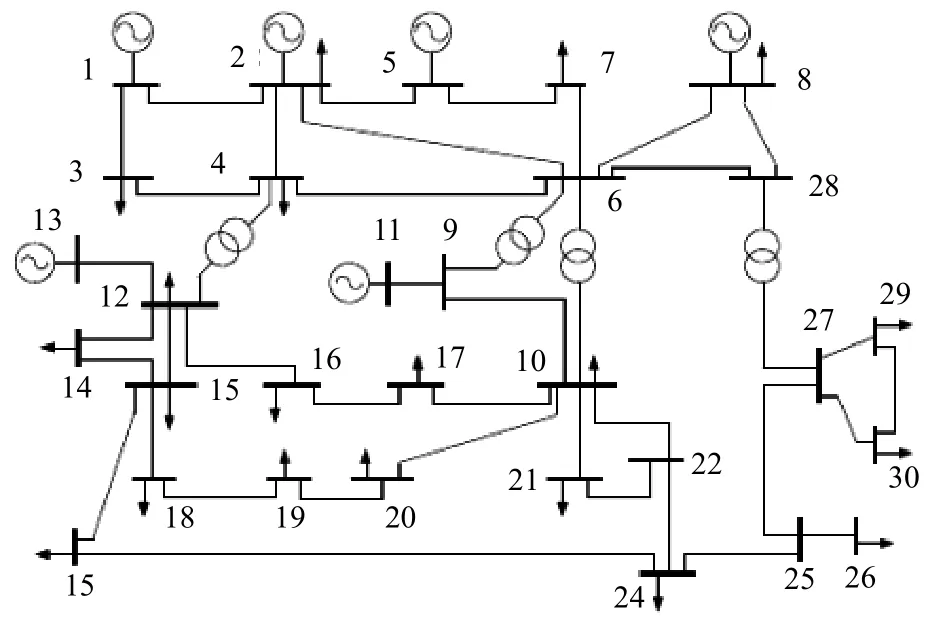
圖10 IEEE-30母線系統(tǒng)

對該系統(tǒng)進行仿真完成本文方法及CUEP法計算結果比較。在運用CUEP法時，對故障中軌跡進行了積分，找到其與穩(wěn)定域邊界的正交點，即CUEP，然后將對應的CUEP（即δ）值代入式（7），計算得到了對應點的勢能極大值。最后將該值代入式（11），獲取了IEEE-30母線系統(tǒng)中三相短路故障發(fā)生在不同點時的能量裕度值。兩種方法的仿真計算時間和計算結果的比較分別如表1和表2所示。

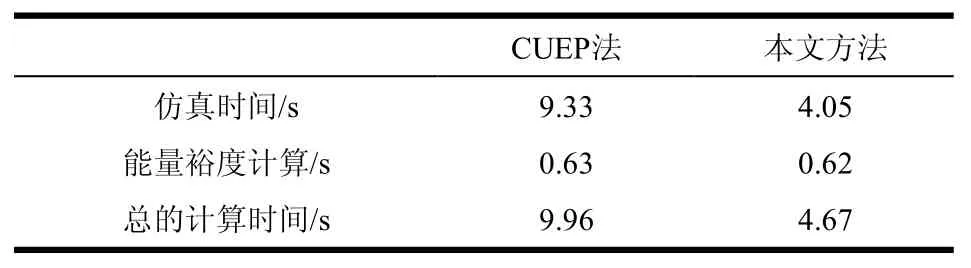
表1 CUEP法和本文方法的計算時間與能量裕度結果比較

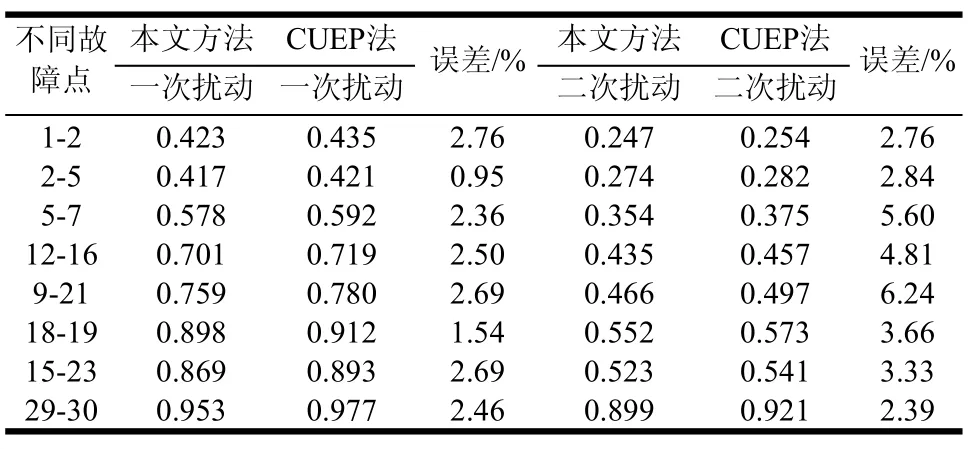
表2 IEEE-30母線系統(tǒng)中基于插值法的PEBS法與CUEP法計算結果的比較

從表1可見，CUEP法的仿真時間明顯長于本文方法，其原因在于故障軌跡積分以求取可控不穩(wěn)定平衡點（CUEP）時需要耗較長時間，而本文方法不需要對故障軌跡進行積分，其耗時主要在實施二次擾動過程。在能量裕度計算上，CUEP法與本文方法消耗時間基本相當，這是因為能量裕度計算過程基本相同，計算量相當。從仿真到裕度計算，CUEP法比本文方法耗費時間多5.29s。從而證明了本文方法在計算速度上有了提高，距離暫態(tài)能量函數(shù)的在線應用又近了一步。

對表2中一次擾動和二次擾動的計算結果縱向對比可知，當三相短路故障發(fā)生在距離發(fā)電機越近或者直接與發(fā)電機相連的支路時，穩(wěn)定裕度越低，如支路1-2、2-5和5-7，相比較于支路12-16、9-21、18-19和15-23，在經(jīng)受了一次擾動和二次擾動后，其穩(wěn)定裕度下降很多，說明這些支路對維持系統(tǒng)的穩(wěn)定性具有重要意義。支路29-30在經(jīng)受一次擾動和二次擾動后，穩(wěn)定裕度最大，該支路對系統(tǒng)穩(wěn)定性影響最小。表2進行橫向比較，無論是一次擾動還是二次擾動，CUEP法得出的能量裕度值明顯大于本文方法的計算結果。原因在于獲取CUEP的過程中，多次積分及步長選取都會導致較大的誤差。而本文方法在二次擾動的過程中，第二次故障恢復后的穩(wěn)定平衡點及CUEP的確定，也會因為大量的計算導致誤差增大。另外，故障地點的選取，對計算結果的精確性也有一定的影響，如表2中所示，不同的故障地點對應的計算結果誤差不同，支路9-21斷開時，誤差為6.24％，達到最大。

5 結束語

本文結合暫態(tài)能量函數(shù)模型，分析了基于二次擾動法的勢能邊界值插值計算法，推導了系統(tǒng)暫態(tài)穩(wěn)定性量化指標，通過在三機系統(tǒng)和IEEE-30母線系統(tǒng)中的仿真結果及其與CUEP法的對比分析表明：基于二次擾動法的勢能邊界值插值計算法，能夠避免直接求取穩(wěn)定域邊界上的不穩(wěn)定平衡點，缺點在于需要保存第一次故障后系統(tǒng)穩(wěn)定時的狀態(tài)參數(shù)并依賴第二次擾動的發(fā)生；基于二次擾動法計算的勢能邊界值，直接受到第二次擾動的持續(xù)時間的影響，即不同的持續(xù)時間得到的勢能邊界值有差異，一定程度上影響結果的精確性；基于二次擾動法的暫態(tài)穩(wěn)定性量化指標，相比較于CUEP法，計算過程簡單，易于理解，計算速度有所提高，能適應不同的系統(tǒng)運行條件，其局限是只能用于暫態(tài)穩(wěn)定性離線分析，下一步的工作是進一步研究基于能量裕度的電力系統(tǒng)暫態(tài)穩(wěn)定性在線評估指標構建。

［1］DONG Z Y，ZHAO J H，HILL D J.Numerical simulation for stochastic transient stability assessment［J］.IEEE Transactions on Power Systems，2012，27（4）：1741-1749.

［2］JAIME C C，JOSé L R，DELIA G C，et al.Real-time transient stability assessment based on centre-of-inertia estimation from phasor measurement unit records［J］.IET Gener Transm Distrib，2014，8（8）：1363-1376.

［3］汪隆君，王鋼.基于動態(tài)安全域與埃奇沃斯級數(shù)的電力系統(tǒng)暫態(tài)穩(wěn)定概率評估［J］.中國電機工程報，2011，31（1）：52-58.

WANG Long-jun，WANG Gang.Probabilistic assessment of transient stability based on dynamic security region and edge worth series［J］.Proceedings of the CSEE，2011，31（1）：52-58.

［4］GUOT Y，MILANOVIC J V.Probabilistic framework for assessing the accuracy of data mining tool for online prediction of transient stability［J］.IEEE Transactions on Power Systems，2014，29（1）：377-385.

［5］FRANCISCO R G，ATHULA D R，UDAYA D A，et al.Support vector machine-based algorithm for post-fault transient stability status prediction using synchronized measurements［J］.IEEE Transactions on Power Systems，2011，26（3）：1474-1482.

［6］葉圣永，王曉茹，劉志剛，等.基于支持向量機增量學習的電力系統(tǒng)暫態(tài)穩(wěn)定評估［J］.電力系統(tǒng)自動化，2011，35（11）：15-19.

YE Sheng-yong，WANG Xiao-ru，LIU Zhi-gang，et al.Power system transient stability assessment based on support vector machine incremental learning method［J］.Automation of Electric Power Systems，2011，35（11）：15-19.

［7］Lü J Q，MIROS?AW P，UDAYA D A.Prediction of the transient stability boundary using the Lasso［J］.IEEE Transactions on Power Systems，2013，28（1）：281-288.

［8］YIN Ming-hui，CHUNG C Y，WONG K P，et al.An improved iterative method for assessment of multi-swing transient stability limit［J］.IEEE Transactions on Power Systems，2011，26（4）：2023-2030.

［9］朱林，徐敏，陳裔生，等.一種改善電力系統(tǒng)暫態(tài)性能的軌跡跟蹤控制策略［J］.電力系統(tǒng)自動化，2012，36（14）：1-5，22.

ZHU Lin，XU Min，CHEN Yi-sheng，et al.A method for improving power system transient performance using estimator resetting based on tracking models［J］.Automation of Electric Power Systems，2012，36（14）：1-5，22.

［10］YAN J，TANG Y F，HE H B，et al.Cascading failure analysis with DC power flow model and transient stability analysis［J］.IEEE Transactions on Power Systems，2015，30（1）：285-295.

［11］汪小明，劉滌塵，吳軍，等.基于能量函數(shù)法的電網(wǎng)暫態(tài)穩(wěn)定性分析［J］.電網(wǎng)技術，2011，35（8）：114-118.

WANG Xiao-ming，LIU Di-chen，WU Jun，et al.Energy function-based power system transient stability analysis［J］.Power System Technology，2011，35（8）：114-118.

［12］董超，劉滌塵，廖清芬，等.基于能量函數(shù)的電網(wǎng)低頻振蕩及擾動源定位研究［J］.電網(wǎng)技術，2012，36（8）：175-181.

DONG Chao，LIU Di-chen，LIAO Qing-fen，et al.Research on low frequency oscillation in power grid and location of disturbance source based on energy function［J］.Power System Technology，2012，36（8）：175-181.

［13］王科，游大海，尹項根，等.基于支路勢能脊的電力系統(tǒng)暫態(tài)穩(wěn)定分析和臨界割集識別［J］.電工技術學報，2013，28（11）：262-269.

WANG Ke，YOU Da-hai，YIN Xiang-gen，et al.Power system transient stability analysis and critical cutset detection based on branch ridge［J］.Transactions of China Electrotechnical Society，2013，28（11）：262-269.

［14］ANGHEL M，F(xiàn)EDERICO M，ANTONIS P.Algorithmic construction of Lyapunov functions for power system stability analysis［J］.IEEE Transactions on Circuits and Systems-I：Regular Papers，2013，60（9）：2533-2546.

［15］WU Y H，MUSAVI M，LERLEY P.Synchrophasor-based monitoring of critical generator buses for transient stability［J］.IEEE Transactions on Power Systems，2015，30（99）：1-9.

［16］汪芳宗，何一帆.基于辛龍格-庫塔-奈斯通方法的電力系統(tǒng)暫態(tài)穩(wěn)定性并行計算方法［J］.電網(wǎng)技術，2011，35（4）：40-45.

WANG Fang-zong，HE Yi-fan.A parallel computational method for power system transient stability based on Symplectic Runge-Kutta-Nystr?m method［J］.Power System Technology，2011，35（4）：40-45.

［17］VAHID J M，ZHOU Z Y，VENKATA D V.Large-scale transient stability simulation of electrical power systems on parallel GPUs［J］.IEEE Transactions on Parallel and Distributed Systems，2012，23（7）：1255-1266.

［18］ROGER T T，VITTAL V，KLIEMANN W.An improved technique to determine the controlling unstable equilibrium point in a power system［J］.IEEE Transactions on Circuits and Systems-I：Fundamental Theory and Applications，1996，43（4）：313-322.

編輯 漆 蓉

Energy-Based Research on Grid Transient Stability Off-Line Quantification Index

LIU Qun-ying1，LIU Qi-fang2，LIU Deng3，and LIAO Yong-feng1
（1.School of Automation Engineering，University of Electronic Science and Technology of China Chengdu 611731；2.China Guodian Sichuan Ashine Power Co.Ltd Chengdu 610021；3.Ziyang Company of Sichuan Electrical Power Company Ziyang Sichuan 641316）

Energy margin based on Lyapunov direct method has been considered as an important index to quantify the transient stability of power system.Especially its on-line application has been focus of attention.Based on the classical equations of rotor motion，the transient energy function model is first established in this paper.Then the converting relationship between the potential energy boundary surface and the stability region characteristics is described.Based on these，the second kick method and the interpolation method based on the property of potential energy boundary are combined to calculate the maximum of the potential energy.At last，the energy margin model is established based on the maximum of potential energy and the transient energy.The simulation results in three-machine and IEEE-30 bus system and the comparison with CUEP verify the effectiveness and feasibility of the proposed method，which can be used in off-line assessment of transient stability of power system.

energy margin；stability region；the second kick；transient stability

TM7

A

10.3969/j.issn.1001-0548.2015.05.012

2014-07-09；

2015-05-25

國家自然科學基金（51007006）；中國博士后面上基金（2015M572457）

劉群英（1977-），女，博士，副教授，主要從事電力系統(tǒng)穩(wěn)定與控制分析方面的研究.