基于航班離港時刻主導的單航班離港旅客聚集模型

邢志偉，馮文星，，羅 謙，李學哲，，白 楠，，潘 野，李定亮（.中國民航大學航空自動化學院 天津 東麗區 300300；.中國民航局第二研究所 成都 6004）

基于航班離港時刻主導的單航班離港旅客聚集模型

邢志偉1，馮文星1，2，羅 謙2，李學哲1，2，白 楠1，2，潘 野2，李定亮2
（1.中國民航大學航空自動化學院 天津 東麗區 300300；2.中國民航局第二研究所 成都 610041）

通過對單航班離港旅客在航站樓聚集行為的動力學分析，證明了旅客的到達聚集行為在群體層面受截止時間影響服從重尾分布，并且存在混合分布特性；揭示了航班截止時間的變化對旅客行為重尾特性的影響規律。在此基礎之上基于對數正態分布與回歸分析建立了航班離港時刻主導的單航班離港旅客聚集模型，并通過仿真驗證證明了模型擬合度達到80％以上，具有工程推廣價值。

群體行為；重尾分布；人類動力學；對數正態分布；模型

近年來我國民航業持續高速發展，據民航局行業發展統計公報顯示，自2010年以來旅客吞吐量平均增速都維持在10％左右，2014年全國民航機場旅客吞吐量達8.32億人次，位居世界第二。與此同時民航機場運行保障評估研究表明，2015年近60個機場達到資源飽和。傳統的依靠資源冗余滿足旅客需求的格局已被打破，旅客過站時間長，服務效率、滿意度下降等現象成為民航機場亟待解決的難題。國內外學者力圖通過研究機場資源配置優化和旅客服務流程優化，提高機場對旅客的服務效率與水平。

文獻［1］采用計算機技術對候機大廳內的旅客流進行仿真并提出優化策略，可以提高候機大廳的利用率以及旅客的滿意度。文獻［2］采用離散事件仿真技術模擬了旅客在航站樓內的流程，在此基礎上預測延誤，為管理人員提供理性的值機與安檢策略。這類研究采用計算機仿真技術實現對航站樓旅客流程的定性分析以及資源優化，在一定程度上緩解了資源緊張。但仿真技術在輸入層都采用理想的旅客到達模型（如泊松分布），忽略航班流等運行因素對旅客流的巨大影響，與現實旅客流相比存在較大誤差。另一類研究側重宏觀角度預測旅客流量，文獻［3］基于模糊理論建立了經濟計量模型很好地預測了希臘機場旅客流量。文獻［4］則將重力模型加以分析利用，建立了預測模型，該模型在已知機場設施條件下很好地改善了預測精度。宏觀角度對旅客流量的預測可以從整體態勢與全局角度把握旅客對機場資源的需求，但基于目前機場資源緊張、松弛空間小的條件下，根據旅客到達聚集狀態，實時調整資源分配才是未來有效解決資源緊張問題的主要手段。

要做到機場資源的實時分配，旅客聚集人數的精確預測必不可少，因此本文通過分析自助值機系統的旅客數據，以微觀角度的單個離港航班為研究對象，對旅客群體層面的動力學進行分析，基于對數正態分布與回歸分析，建立了基于航班離港時刻主導的單航班旅客聚集模型。經驗證，該模型與真實數據擬合度達到80％以上，為航站樓內各區域旅客聚集人數的精確預測及服務流程優化研究奠定了基礎。

1 旅客到達規律分析

人類動力學對人類行為做了大量研究，發現由于存在截止時間、個人喜好、排隊優先權等因素的影響，人類的日常通信、瀏覽網站、圖書借閱等行為呈現非泊松統計特性，服從重尾分布［5-6］。科學界通過總結這些問題，基于排隊優先權、人類自身興趣與記憶因素分別建立了數學模型［6-8］。然而針對截止時間影響的人類行為，很少有公認的數學模型。關于人類群體行為的預測，文獻［9］引入截止時間，建立了簡單數學模型預測參加會議的注冊人數。研究發現，注冊人數的增長通常不是線性而是在會議前幾天呈現爆發式增長［9］。本文通過研究旅客群體層面在航站樓的聚集行為，說明了旅客到達行為服從重尾分布，但有區別于基于排隊優先權的兩大普適類。

以下是對航站樓內旅客到達規律統計，數據來源于某航空公司的自助值機系統。據統計，旅客到達航站樓后，如果通過自助方式值機，基本不需要等待。因此本文用旅客自助值機時間作為旅客到達時間，以自助值機旅客作為樣本點，刻畫旅客總體到達規律。旅客總體的到達規律如圖1所示，圖中橫軸表示提前時間即等待時間tw，原點表示航班起飛時刻t0，t為旅客自助值機時間，則有tw=t0?t（為方便時刻與時間段統一計算，將其全部轉換為小于1的比例數，即相對時間，下同）。縱軸表示平均到達率，圖中每個小矩形的面積表示單位時間到達的旅客比例。由圖可見旅客在航站樓的到達行為有很強的非均勻性并且活躍性［11］隨時間變化劇烈，平均到達率曲線拖著長長的尾巴有明顯的重尾特性。

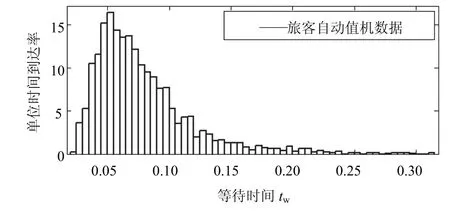
圖1 旅客平均到達分布

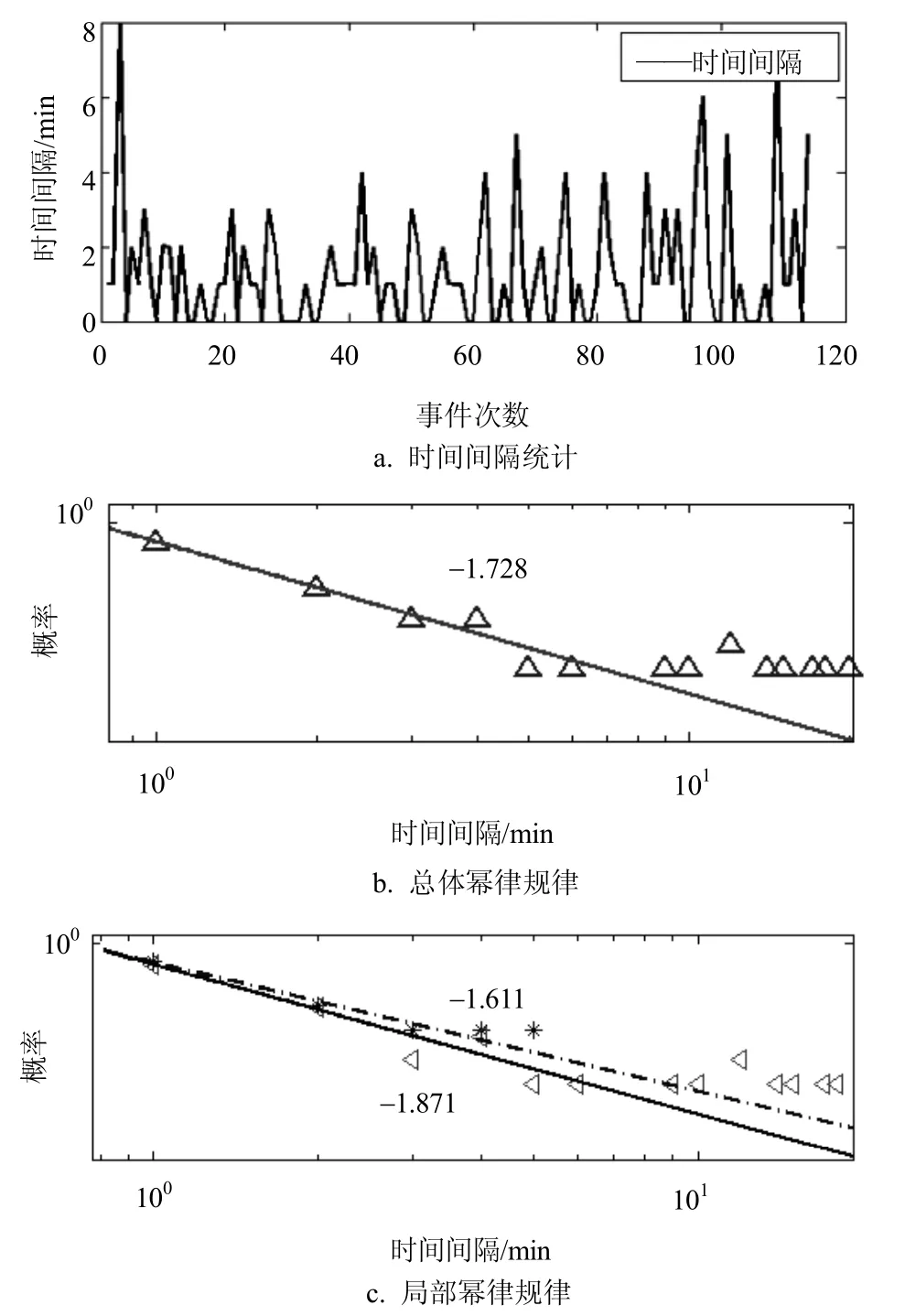
圖2 旅客到達時間間隔統計

圖2a為旅客到達航站樓的時間間隔統計，橫軸為事件發生次數，縱軸表示時間間隔τ，其總體服從冪指數為?1.728的冪律分布如圖2b所示。將旅客從眾數tm拆分加以分析，前半部分服從冪指數為?1.611的冪律分布，后半部分服從冪指數為?1.871的冪律分布如圖2c所示，說明旅客到達規律具有重尾特性，并且在旅客航站樓聚集這一問題上有著多重標度，不能用單一模式刻畫，有著混合分布的特征。根據大量數據分析，其總體冪律特性受干擾因素影響不斷變化，但其總體冪指數在［?1.5，?2］區間內。明顯區別于文獻［8］的重尾分布兩大普適類。

2 基于對數正態分布的旅客模型

對數正態分布為重尾分布中比較重要的成員之一，它是典型的混合分布，其廣泛用于經濟學分析，也有少量學者用它刻畫重尾分布，但一直作為人類動力學的非主流存在。

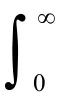
定義2 如果隨機變量X的對數lnX服從正態分布，則稱X服從參數為μ和σ2的對數正態分布［12］。其概率密度函數為：

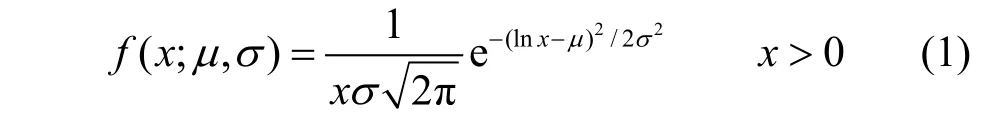
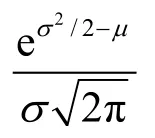
將旅客數據與式（1）進行數據擬合，并做擬合優度檢驗。隨機抽取12個航班的旅客數據進行擬合，結果如表1所示，其中與為對數正態分布的參數估計值。對于原假設H0：旅客等待時間服從對數正態分布，對于假設H1：旅客等待時間不符合對數正態分布。p為擬合優度檢驗值，由p值可判斷是否拒絕原假設。H=1表示拒絕原假設，H=0表示不拒絕原假設，顯著性水平均默認?=0.05。如表1所示，超過83％的離港航班旅客等待時間通過擬合優度檢驗，不拒絕對數正態分布。從數據層面說明了離港旅客的到達為行服從對數正態分布。

綜上分析，建立基于對數正態分布的單航班離港旅客聚集模型（arrived passenger model in sngle flight，SFAPM）：

設t0為航班預計離港時刻，tw為提前時間，t為任一航班起飛前時刻。則P（t0?t）即P（tw）為t時刻旅客累積到達比例，且P（tw）滿足以下關系：

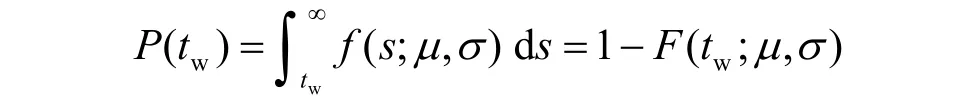
即：

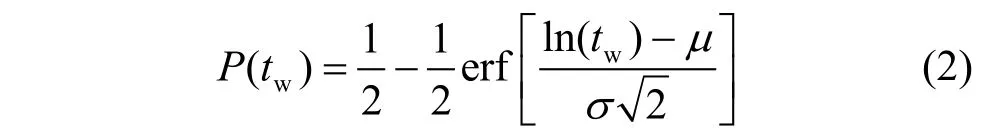
式中，μ與σ為待定參數。

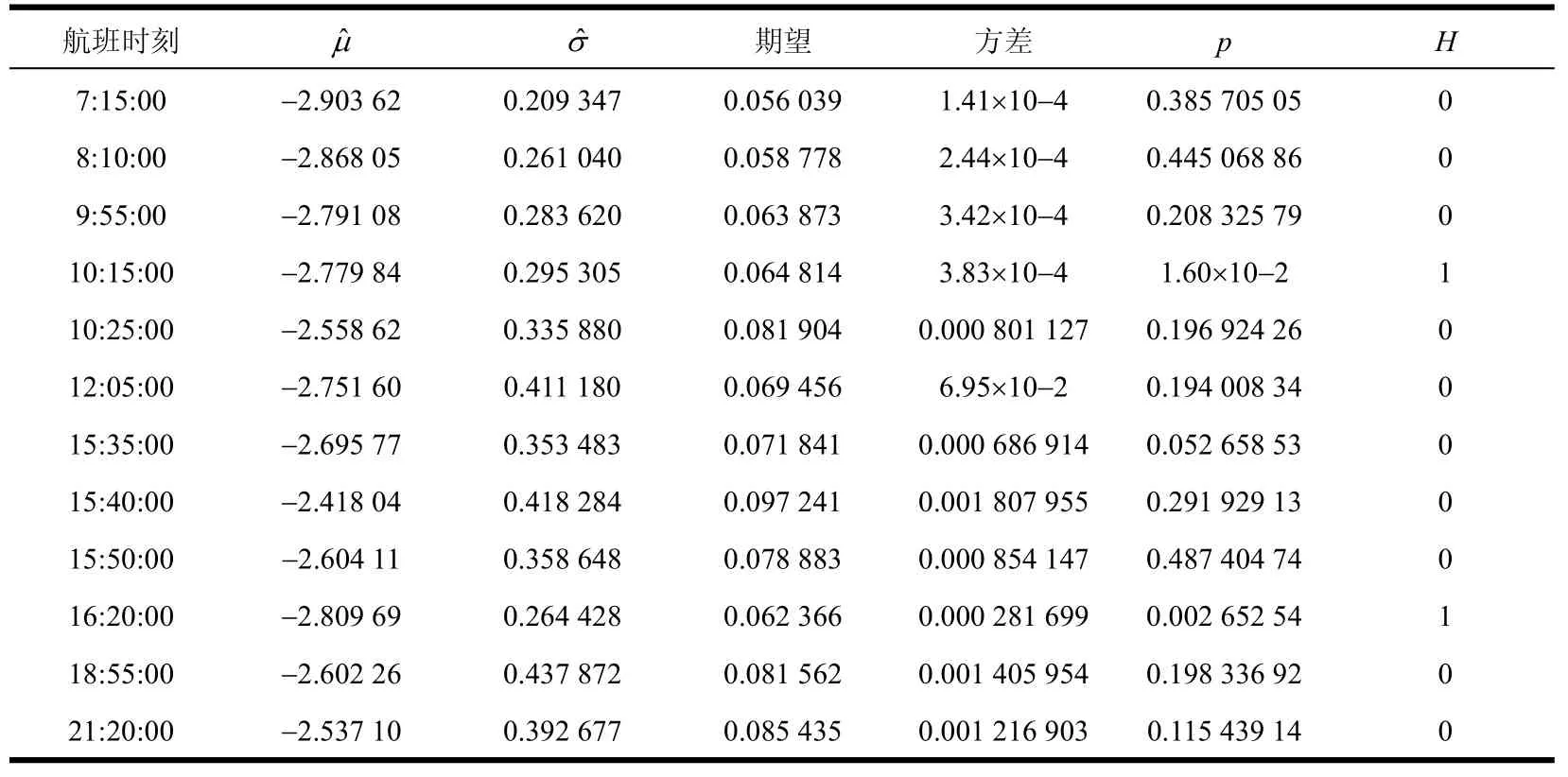
表1 擬合優度檢驗

由表1可見，由于受到多種因素影響，對數正態分布參數上下浮動較大。為了更直觀了解參數變化給分布帶來的影響，給出重尾強度D與分布范圍R定義。

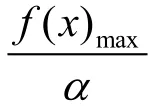
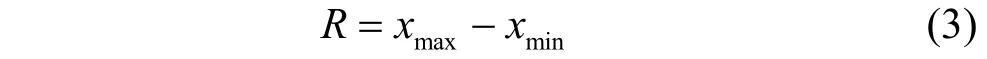
并且必存在最大值轉折點xm，則重尾強度定義為：

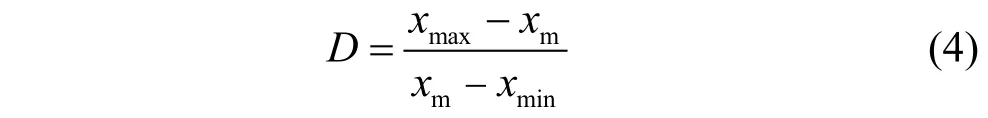
當該分布為正態分布時D=1，即不是重尾分布；當該分布為重尾分布時D＞1，并且重尾特性越強，分布尾巴越長D值越大。通過這兩個值能對參數變化帶來的影響有更直觀的了解。

將定義3應用于對數正態分布，有：

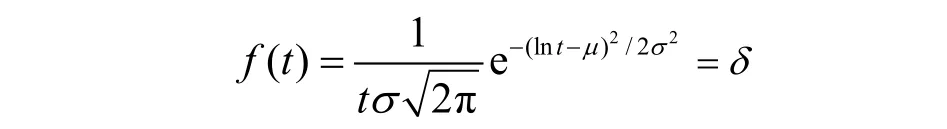
解得：

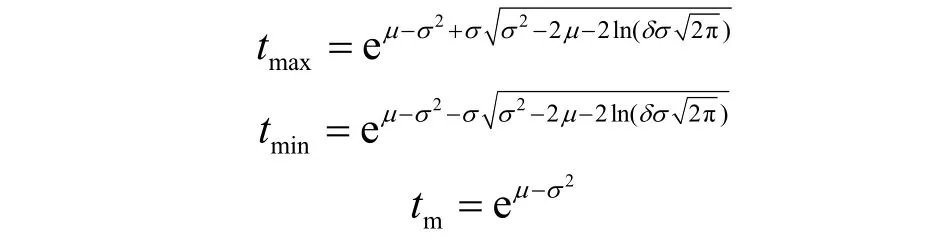
使a=40，將上述結果帶入式（3）、式（4），有；

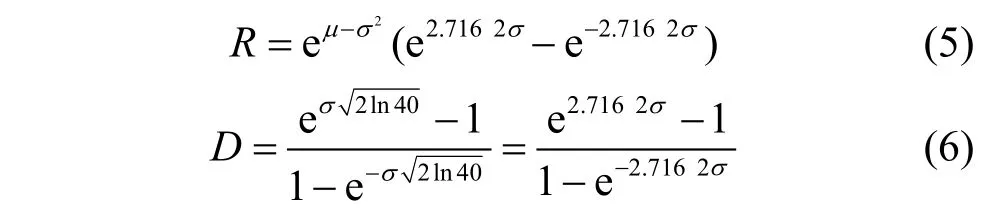
由式（5）可知，對數正態分布的分布范圍由兩個參數共同決定，并且μ起主導作用。由式（6）可知，重尾強度僅與σ有關，并且為嚴格的單調遞增關系，即σ值越大重尾特性越強，冪律尾巴越長。

本文經過對旅客數據的分析證明了旅客群體層面的到達規律服從對數正態分布，并且基于對數正態分布建立了單航班離港旅客聚集模型（SFAPM），但由于受到多種因素影響對數正態分布的重尾強度與分布范圍有很大波動，對影響因素加以分析才能進一步揭示旅客行為規律。

3 基于航班離港時刻的影響因素分析

影響旅客聚集的因素眾多，包括時間因素、空間因素與突發因素等。本文只在時間維度考慮對旅客行為的影響，因此有如下假設：

1）旅客數據均來自同一機場。

2）航班容量相同。

3）航線性質相同（國內航班）。

4）旅客出行當天無天氣異常等突發因素。

根據假設旅客受到時間維度的影響主要有t0（航班離港時刻）與M（月份）。不同于多元回歸分析，旅客在航站樓聚集的總體規律服從對數正態分布，因此本文基于對數正態分布研究時間維度參量變化引起的分布變化。

根據定義3，隨機抽取一個航班，由航班月份變化引起的重尾強度與分布范圍變化如表2所示，由表可以看出由航班月份變化引起的分布變化非常小，因此將航班季度因素作為弱影響因素排除。

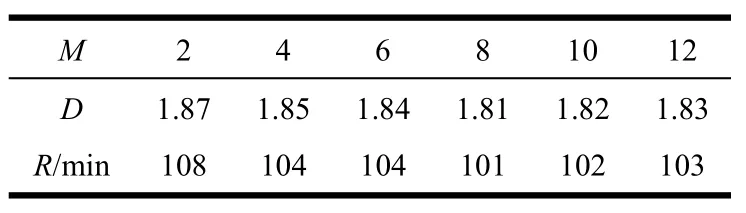
表2 月份變化引起的分布變化

航班離港時刻對分布的影響如圖3所示，由圖可以看到分布的分布范圍R與重尾強度D受航班時刻影響變化非常明顯，說明在建模過程中航班離港時刻作為主要影響因素不可忽略。并且在圖中還可以看到由于受到航班離港時刻的影響，旅客聚集行為的時間分布范圍與重尾強度均呈現明顯的遞增趨勢，即旅客行為的重尾特性會隨著離港時刻的推移逐漸增強，這個發現不僅為本文的建模提供依據，并且該規律也為交通運輸類人類動力學建模提供一定參考。

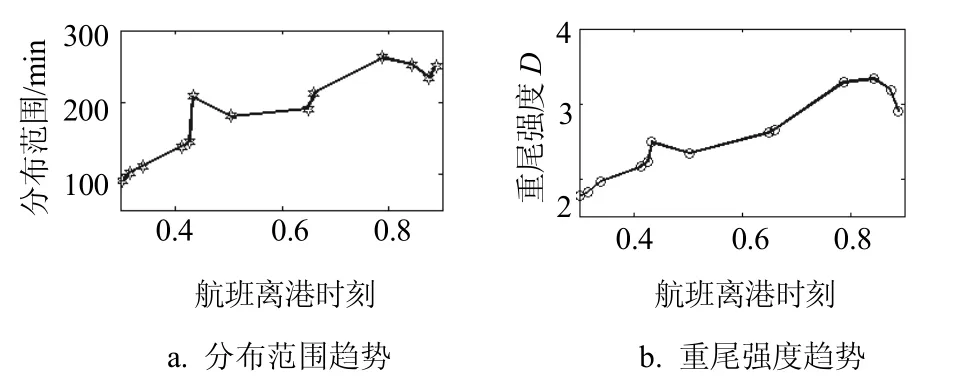
圖3 參數變化對分布的影響

經分析由航班離港時刻引起的分布參數變化總體上呈現多項式特征。對μ和σ進行回歸分析，結果如下：

μ分析結果為：

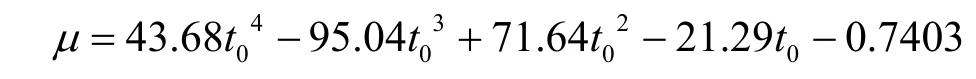
σ分析結果為：

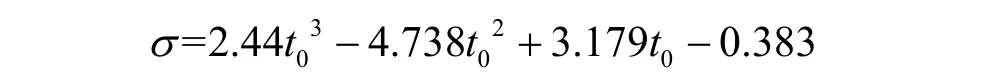
綜上分析，結合SFAPM模型建立航班離港時刻主導的單航班離港旅客聚集模型（arrived passenger model in single flight based on the time of departure，TD-SFAPM）為：

設t0為航班計劃離港時刻，t為任一航班起飛前時刻。根據SFAPM模型，在t時刻旅客累積到達比例滿足以下關系：

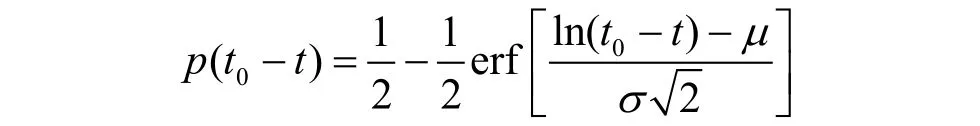
且其參數μ與σ可由離港航班時刻t0唯一決定，有：

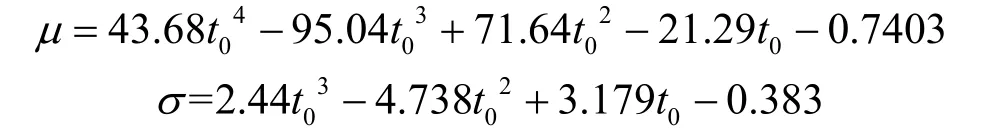
設航班的容量為S，航班上座率為λ，則在t時刻，旅客在航站樓聚集的人數為：

Q=SλP（t0?t）

本節根據旅客行為的重尾特性，基于SFAPM模型與回歸分析，建立了航班離港時刻主導的旅客到達聚集模型（TD-SFAPM）。該模型既具有重尾特性與混合分布特點，還可以根據離港航班時刻調整參數，適應重尾強度與分布范圍的變化。

4 模型驗證與分析

4.1 模型驗證

根據上文所建立的TD-SFAPM數學模型，將未參與建模分析的航班數據（數據分布在12個月中的26個航班）作為驗證集，參與模型驗證。隨機抽取3個航班，并且每個航班都分布在不同的月份。實驗在MATLAB環境中進行，驗證結果如圖4所示。

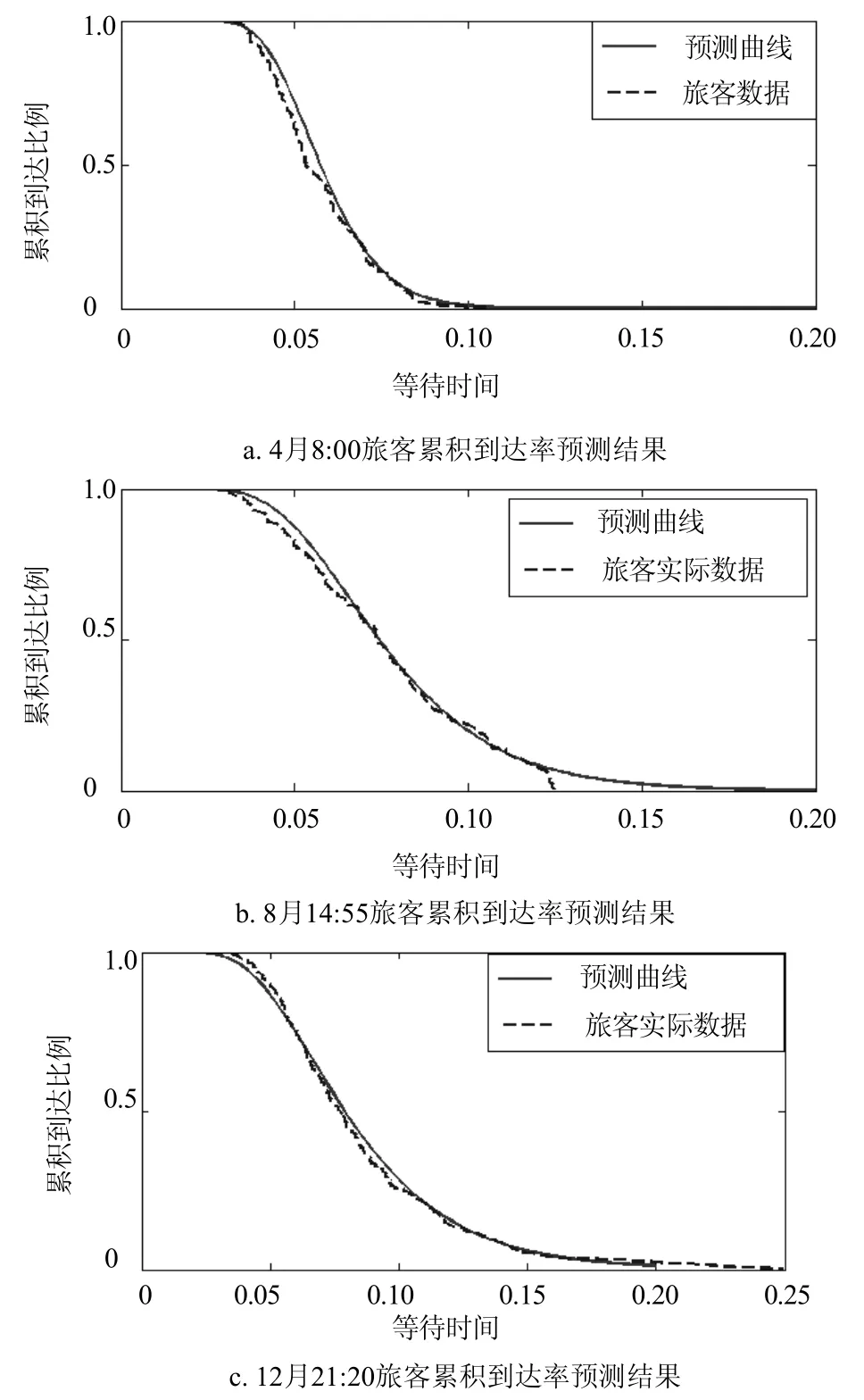
圖4 模型驗證結果

檢驗的航班包含4月8：00：00、8月14：55：00、12月21：20：00，包含上午、下午以及晚上的3個不同月份與時刻。仿真表明，模型可以根據航班時刻的變化自動調整參數，進而改變模型變化率。在時間維度有很好的契合效果，模型與真實數據的平均擬合度達到80％以上，顯示了模型較好的預測能力。同時，由于3個航班分布在不同月份，其良好的預測效果也證明了上文提到的觀點，航班月份的變化作為弱影響因素可以忽略不計。

4.2 模型對比

SFAPM為典型的固定參數模型，為了證明參數自調整環節對模型精度的影響，將上文使用的3個航班數據作為驗證數據，采用SFAPM作為預測模型，在相同的環境下對3個航班進行仿真預測并對比，仿真結果如圖5a所示。在預測的3個航班中，只有14：55：00的航班擬合度為82％，8：00：00的航班擬合度只有11％，21：20：00的航班擬合度為35％。與圖4對比有以下結論：SFAPM為典型的固定參數模型，雖然模型也符合旅客的行為規律，但在旅客重尾特性時變的條件下，不可調整參數使得模型的精度難以保證。對比上文實驗，加入參數自調整環節后，模型預測精度在某些時段有了質的提升，可以較好地預測各時段的航班旅客聚集人數，具有較好的適應性。

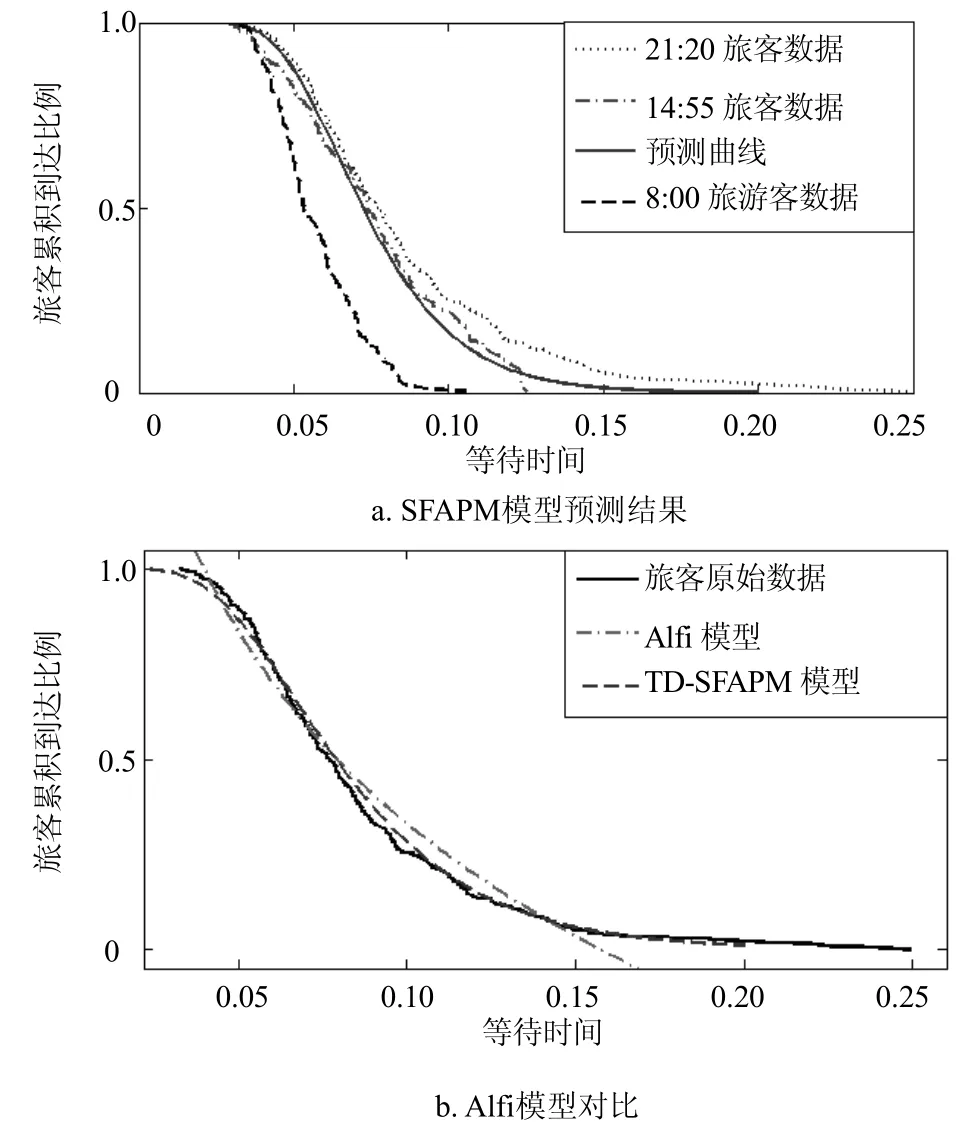
圖5 模型對比仿真

綜上所述，TD-SFAPM模型擁有兩個方面的優勢：1）模型有參數自調整環節；2）模型有重尾特性與混合分布特點。這兩個優勢使得模型緊密結合旅客行為規律，預測精度上得以保障。

5 總結

本文首先通過對單航班離港旅客自助值機數據分析，說明了旅客聚集規律服從重尾分布，證明了旅客聚集規律服從對數正態分布，從數據角度說明了對數正態分布在交通領域人類動力學建模的可用性，并且建立了以航班離港時刻主導的單航班旅客聚集模型（TD-SFAPM）。仿真結果顯示模型具有較高的預測精度，為實時掌握旅客在航站樓的聚集動態提供了可能。其次經分析隨著航班離港時刻的推移，旅客聚集的重尾強度與分布范圍逐漸增加，說明了人類行為受到不同截止時間影響其重尾特性不同，這也為交通運輸人類動力學建模提供一定參考。最后需要指出的是影響旅客聚集規律的因素還有很多，本文只在時間維度范疇內考慮了主要影響因素，其他影響因素還有待進一步探索。

［1］CASAS P F，CASANOVAS J.Passenger flow simulation in a hub airport：an application to the Barcelona international airport［J］.Simulation Modelling Practice and Theory，2014，44：78-94.

［2］GUIZZI G，MURINO T，ROMANO E.A discrete event simulation to model passenger flow in the airport terminal［J］.Mathematic Methods and Applied Computing，2012，40（1）：427-434.

［3］PROFILLIDIS V A，BOTZORIS G N.A comparative analysis of performances of econometric，fuzzy and time-series models for the forecast of transport demand［C］//Fuzzy Systems Conference，2007.［S.l.］：IEEE，2007：1-6.

［4］GROSCHE T，ROTHLAUF F.Armin heinzl gravity models for airline passenger volume estimation［J］.Journal of Air Transport Management，2007，13：175-183.

［5］韓筱璞，汪秉宏，周濤.人類行為動力學研究［J］.復雜系統與復雜性科學，2010，7（3）：132-144.

HAN Xiao-pu，WANG Bing-hong，ZHOU Tao.Researches of human dynamics［J］.Complex System and Complex Science，2010，7（3）：132-144.

［6］周濤，韓筱璞.人類行為時空特性的統計力學［J］.電子科技大學學報，2013，42（4）：481-540.

ZHOU Tao，HAN Xiao-pu.Statistical mechanics on temporal and spatial activities of human［J］.Journal of University of Electronic Science and Technology of China，2013，42（4）：481-540.

［7］VáZQUEZ A，OLIVEIRA J G，DEZS Z，et al.Modeling bursts and heavy tails in human dynamics［J］.Phys Rev E，2006，73（3）：036127.

［8］GOH K I，BARABáSI A L.Burstiness and memory in complex systems［J］.Europhys Lett，2008，81（4）：48002.

［9］ALFI V，GABRIELLI A，PIETRONERO L.How people react to a deadline［J］.Central European Journal of Physics，2009，7（3）：483-489.

［10］LEPAGE R.Heavy-tailed distributions［J］.International Encyclopedia of Statistical Science，2014（2）：626-628.

［11］ZHOU T，KIET H A T，KIM B J，et al.Role of activity in human dynamics［J］.Europhysics Letters，2008，82（2）：28-32.

［12］邊寬江，崔冰，金曉燕.對數正態分布的VAR數學模型及其計算［J］.數學的實踐與認識，2011，41（1）：11-16.

BIAN Kuang-jiang，CUI Bing，JIN Xiao-yan.Varmathematical model and its computing methods under the lognormal distribution［J］.Mathematics Knowledge and Practice，2011，41（1）：11-16.

編輯 漆 蓉

Arrived Passenger Model in Single Flight Based on the Time of Departure

XING Zhi-wei1，FENG Wen-xing1，2，LUO Qian2，LI Xue-zhe1，2，BAI Nan1，2，PAN Ye2， and LI Ding-liang2
（1.Aeronautical Automation College，Civil Aviation University of China Dongli Tianjin 300300；2.The Second Research Institute of Civil Aviation administration of China Chengdu 610041）

The arrival aggregation behavior of a single flight departing passengers at the group level affected by the deadline is proved to obey heavy-tailed distribution with mixed distribution characteristics through the dynamics analysis about the passengers’behavior at Terminal.The influence of the changes of flight deadline on the heavy tail characteristics of passengers’behavior is studied.On this basis，the arrived passenger model in single flight based on the time of departure（TD-SFAPM）is built，on account of the log-normal distribution and the regression analysis.The accuracy of the model is proved to be more than 80 percent by simulation.

group behavior；heavy-tailed distribution；human dynamics；log-normal distribution；model

U8

A

10.3969/j.issn.1001-0548.2015.05.014

2015-03-25；

2015-06-25

國家科技支撐計劃（2012BAG04B02）；國家自然科學基金委員會與中國民用航空局聯合項目（U1233118，U1333122）；中央高校基金（3122014P003）

邢志偉（1970-），男，博士，研究員，主要從事民航裝備與系統、民航智能規劃與調度方面的研究.