基于舟山外海連續測站的湍混合研究*

史軍強，陳學恩

（中國海洋大學海洋環境學院，山東 青島 266100）

湍流是海洋中普遍存在的一種高度無序的、隨機的、非線性的高頻流動，被認為是經典物理中最后一個未被解決的難題。湍流混合在對海洋能量和水體的交換的轉變過程中起著至關重要的作用，它可以引起海洋動量、熱量、物質在水平和鉛直方向的傳輸，使海水的各種性質趨向均勻，是海洋中眾多物理、生化過程的核心。它的影響不僅僅限于海洋本身，研究發現，湍流混合同樣對全球氣候系統的維持與變化有著重要影響［1］。海洋的內部混合已經成為制約海洋科學、大氣科學等相關領域研究的關鍵和瓶頸。因此，對海洋湍混合的研究也自然成為了當前物理海洋學諸多研究中的意義重大的熱點問題。

陸架海是全球海洋動力過程最為活躍的部分。Egbert和Ray指出，全球潮能耗散的60%～70%發生在陸架海［2］。同時，陸架海也是與人類生存和發展最為密切相關的海域，占全球海洋總面積8%的陸架海是海洋初級生產力最為密集的區域，貢獻了全球初級生產力的15%～30%，全球90%的漁業資源均來自于陸架海。此外，陸架海也是人類從事航運、石油鉆探開采等生產活動的重要場所。因此，開展陸架海的湍混合研究無論在學術領域還是在經濟領域都有著重要的意義和價值。

雖然混合的觀測與研究已得到廣泛的開展，但是，中國近海由于觀測資料有限，湍混合研究仍然較為少見。鐘貽森等利用夏冬兩季黃東海水文與微結構觀測資料，分析了黃、東海域湍流混合與雙擴散現象的空間分布特征與季節變化，指出黃東海陸架湍流混合除了與風應力、底摩擦等外界強迫條件有關外還與局地環流和水團有密切聯系［3］。劉志宇從觀測資料出發，給出了黃海湍流混合變化特征，通過計算表明，黃海底邊界層存在很強的湍耗散并且具有明顯的周期變化規律［4］。在南海海域，盧著敏等利用LADCP與CTD資料對南海中深層混合進行估計，對由垂向翻轉引起的混合進行分析，結果表明，研究海域中深層存在較頻繁的垂向翻轉，翻轉所對應的混合率并不隨深度的增加而減少［5］。上述成果加深了人們對中國近海湍混合特征的了解和認識。

為了研究潮流占優的陸架淺海區冬春轉換季節的湍混合特征，本文利用2010年4月3日舟山外海A站（29.599°N，123.211°E）進行的一次周日（25h）定點連續觀測數據，計算了Thorpe位移、Thorpe尺度、湍動能耗散率、湍混合率等混合參數并探討了其顯著周期及時空變化規律，定量地揭示了該季節舟山外海的湍混合特征。

1 觀測與數據介紹

中國海洋大學“東方紅2”科學考察船于2010年4月1日～6日在杭州灣外的舟山海域進行了為期6d的海洋綜合調查，并于4月3日7時～4日7時（北京時）在A站點（水深68m）（見圖1）進行了連續25h的流速、溫度、鹽度、密度及壓力等要素的觀測。已有的水文分析和短期的測流結果表明，臺灣暖流在東海西部陸架終年存在并且沿50～100m等深線向北流動［6］。由于A站點所處位置正處于臺灣暖流核心流域范圍內，海況復雜，同時A站點位于中國最大漁場——舟山漁場的范圍之內，因此，對該站點湍混合的研究具有重要性、典型性和代表性。A站點流速采用頻率為300kHz的LADCP進行觀測，其發射角為20°，共有4個發射波束，單次測量40層，每層的厚度為2m。每小時觀測一次。由于LADCP的探測信號能夠到達海底，因此可以根據每一層相對于海底的底跟蹤流速以剪切法分別求取每一層的流速。原始觀測的數據為二進制格式，以BBLIST軟件進行格式轉換并設置輸出形式。對所得數據進行質量控制：

（1）設定U、V、U-error、V-error＜99.99，剔除無資料的觀測；

（2）設定percentage＞85，去掉品質不好的觀測；

（3）設定U、V的絕對值小于1.5m/s，誤差絕對值小于0.5m/s。

經過上述的質量控制，對每2m層厚度內的數據取平均，得到的最終海流數據用于本文的分析。

A站點的溫度、鹽度、密度、壓力數據使用美國Seabird公司生產的CTD溫鹽深儀進行測量。使用儀器自帶的SBEDataPocessingWin32軟件對原始數據進行處理［7］，處理步驟包括：工程量轉換、滯后訂正、熱通量訂正、異常值剔除、低通濾波、消除逆壓、平均處理。最終，得到時間分辨率為1h，垂向分辨率為1m的溫度、鹽度、密度、壓力數據。

觀測期間的A站點的水位數據（相對于平均海面）及10m風場數據如圖2所示。其中水位與風場數據的采樣時間均為1h。

圖1 觀測點位置（■A）及地形Fig.1 Observation station（■A）and topography

圖2 觀測期間A站點處的水位序列（上）、風向（下左）及風速（下右）序列Fig.2 Time series of water elevation，wind direction and wind speed at A station

可以看出，在觀測期間水位最大值為1.67m，共出現了2次高潮和2次低潮。相鄰2個波峰/波谷的時間間隔約為12.5h，表現出明顯的正規半日潮特征。風向在前3h為西南風，其余時間均為西北風。最小風速為3.7m/s，最大為7.1m/s。

2 數據分析和討論

2.1 湍流垂向翻轉

在層結湍流中，Thorpe尺度LT通常用來表征湍流所致的垂向翻轉［8］。通常所知，在層結穩定的水體中，位密度剖面的結構必定是從海面的最小值由小到大排列至海底，如果有發生位密度翻轉的情形即密度較大的值對應的深度比密度較小值對應的深度淺或反之，則可視為湍流擾動的結果。本文采用Thorpe提出的算法來估計LT［9］。先將觀測到的位密度剖面重新排列得到分層穩定的剖面，則位密度的原位置與重排之后的位置之間的距離稱為Thorpe位移，通常位移是一段一段地分布在剖面上，每一段的前后皆為零，本文將每一段稱為一個位密度翻轉事件。LT則被定義為每一段Thorpe位移的均方根。以第15小時的觀測數據為例，計算過程如圖3所示。

其中，圖3（a）是重排前后位密度的剖面對比圖，由于圖例比例的原因，圖中位密度剖面重排前后的差別不明顯。圖3（b）則是將圖3（a）在56～66m的深度范圍上進行了放大，可以看到，圖中同一深度處都對應著的不同的位密度，這就是密度的波動。圖3（c）即是由密度波動得到的Thorpe位移。圖3（d）則是根據Thorpe位移計算得到的Thorpe尺度的垂向分布。需要說明的是，在Thorpe位移與Thorpe尺度的垂向分布圖中有很多零值點，這并不是說在這些點對應的深度上不存在湍流翻轉，而是受分辨率限制，無法分辨小于1m的翻轉。圖4（a）為Thorpe尺度的時空分布圖以及水位的時間序列。

圖3 Thorpe算法示意圖Fig.3 Schematic diagram of Thorpe method

結果顯示，Thorpe尺度在垂向上呈現出明顯的分層，上層最大，下層次之中層最小，最大值可以達到11.17m且Thorpe尺度的大值均出現在水位序列的峰值附近。對Thorpe尺度做垂向平均并對其垂向平均時間序列（見圖4（b））進行功率譜分析（見圖4（c））表明，垂向平均的Thorpe尺度具有顯著的半日周期、1/4日周期及2.4h的周期，其中半日周期最為顯著。上述分析說明，湍流翻轉與潮汐關系密切。按照漲潮落潮時間分別計算整層的Thorpe尺度發現，漲潮時段內平均Thorpe尺度為3.44m，而落潮時段內的平均Thorpe尺度僅有2.1m，漲潮的湍流翻轉明顯大于落潮時的湍流翻轉。

2.2 Brunt-Vaisala頻率

在對湍耗散與湍混合進行評估之前首先要計算Brunt-Vaisala頻率。Brunt-Vaisala頻率是指在層結穩定的海洋中，海水微團受到某種力的干擾后，在鉛直方向自由振蕩的頻率［10］。它主要決定于海水密度的鉛直梯度dρ/dZ，近似計算公式為：

因此，本文可以根據前文得到的重新排列后的密度剖面來計算Brunt-Vaisala頻率。圖5即為計算得到的Brunt-Vaisala頻率垂向分布隨時間的變化。

圖中可以看出，Brunt-Vaisala頻率的大值部分呈現出兩條明顯的帶狀分布，一條在15～35m深度范圍內波動，另一條在40～55m深度范圍內波動，且上層帶狀內Brunt-Vaisala頻率的強度要明顯大于下層帶狀內的強度。經計算可得，上、下兩帶狀區域觀測時間內平均的密度垂直梯度分別為0.197和0.04kg/m4，均在《海洋調查規范》所規定的強弱密度躍層臨界值之上［11］，這表明該站點在觀測期間鉛直方向上呈現出了顯著的雙密度躍層結構。為方便下文分析，本文將兩密度躍層中Brunt-Vaisala頻率最大值所在位置稱為密度躍層核心深度。求取每個觀測時刻兩密度躍層中Brunt-Vaisala頻率最大值所在位置，即可得到圖6（a）所示的兩密度躍層核心深度的時間序列。可以看到兩核心深度隨時間均出現不同程度的的起伏，表現出明顯的湍擾動特征。為此，分別對這2個時間序列進行功率譜分析，結果分別繪于圖6（b）（強躍層）、圖6（c）（弱躍層）。結果顯示，強密度躍層核心深度序列的顯著譜峰主要集中在周期為3～5h、9～17h的范圍內，其中在4.4和11h周期處存在最顯著的譜峰，這說明在強密度躍層中表現出了明顯的高頻內波和近半日潮頻率的內潮特征。弱密度躍層核心深度序列的顯著譜峰主要集中在周期為5～22h的范圍內，其中在22h周期處譜峰最為顯著，其次是11h周期處。可見，與強密度躍層有所不同，弱密度躍層中則是近慣性頻率的內波和近半日潮頻率的內潮特征明顯。汪嘉寧和魏皓等也曾通過對東海陸架一連續測站的春季水文環境的日變化特征分析得到過類似的結論［12］。

圖4 Thorpe尺度時空分布及水位時間序列（圖中黑線）（a），Thorpe尺度垂向平均時間序列（b），對Thorpe尺度垂向平均時間序列的功率譜分析（虛線為95%信度水平閾值線）（c）Fig.4 Distribution of Thorpe scale and time series of water elevation（a），vertical averaged Thorpe scale（b）and spectrum analysis for vertical averaged Thorpe scale（c）

圖5 Brunt-Vaisala頻率時空分布Fig.5 Temporal and spatial distribution of Brunt-Vaisala frequency

圖6 密度躍層核心深度（a）及其譜分析結果（b，c）Fig.6 Distribution of spring layer center（a）and spectrum analysis（b，c）

2.3 湍耗散與湍混合

根據上文估算出的Thorpe尺度LT和Brunt－Vaisala頻率N，依據Dillon和Osborn［13］提出的公式

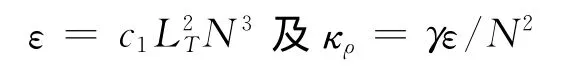
來估算湍動能耗散率ε和湍混合率κρ，其中：c1為經驗常數，一般取為0.64；γ為混合系數，一般取為0.2。圖7為計算所得深度平均的湍動能耗散率ε和湍混合率κρ的時間序列。

湍動能耗散率與湍混合率的時空分布分別如圖8（a）、（b）所示。圖中黑色曲線為上文所得到的強、弱密度躍層的核心深度曲線。在觀測數據覆蓋的25h，即一個周日的觀測期間，該區域的湍動能耗散率平均為2.79×10－7W/kg，量級在10－10～10－6W/kg之間變化。湍混合率平均值為7.1×1 0－4m2/s，量級在10－5～10－2m2/s之間變動。

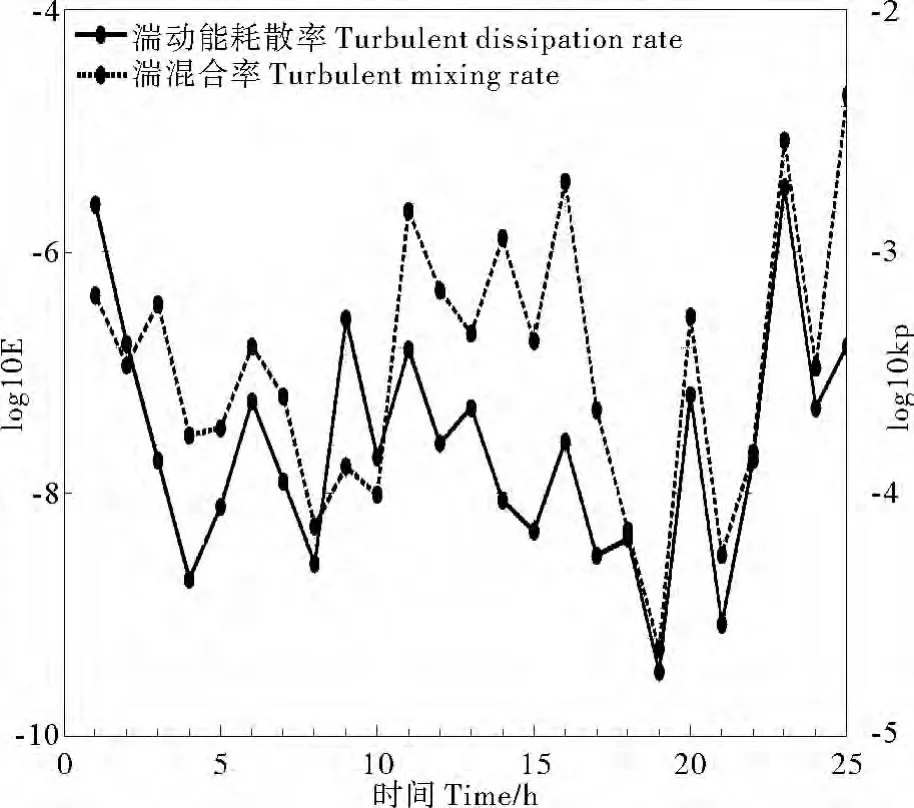
圖7 深度平均的ε與κρ時間序列Fig.7 Time series ofεandκρ

圖8 湍動能耗散率（取對數，W/kg）時空分布（a）與混合率（取對數，m2/s）時空分布（b）Fig.8 Temporal and spatial distribution of turbulent dissipation rateε（a）and turbulent mixing rateκρ （b）（in log unit）

圖中湍動能耗散率與湍混合率的時空分布基本一致，均以密度躍層核心深度曲線為界呈現出明顯的上、中、下3層結構。無論是湍動能耗散率還是湍混合率，其強度均是在上層最大，下層次之中層最小，這從物理上也容易理解，中層上下均以密度躍層的核心深度為界，層結最強，水體最穩定，因而對湍的抑制作用也最強烈，穿越等密度面的小尺度過程要克服層結的抑制作用需要更多的能量；上層水體極易受到海表面風應力等多種動力因素的影響；下層水體由于以海底為下邊界顯然要受到底應力作用的影響。而上躍層層結更強，穿越等密度面的小尺度過程要克服層結的抑制作用需要更多的能量。此外，從圖中還可以看出，中層水體湍動能耗散率與湍混合率強度在觀測的大多數時刻均接近于零，但是在個別時刻存在著間歇性的強混合現象。與躍層的限制作用相反，內波混合可以為環境要素跨躍層交換提供能量，而躍層的存在又為內波的產生提供了條件。本文在前面已證實，在中層水體上下邊界內波活動活躍，尤其以高頻內波、近半日潮頻率的內潮和近慣性頻率的內波信號最為顯著。已有的研究表明，在層化季節，內潮、近慣性內波以及高頻內波的剪切不穩定可以在水體內部造成間歇性的強混合，內波可能是促進該層水體湍混合的一個重要因素，但是對于造成間歇性強混合的機制至今尚不清楚。

2.4 湍混合特征及其影響因子

由于湍動能耗散率的時空分布特征與湍混合率基本一致，因此，本文只對湍混合率進行分析，并著重揭示研究海域上層和下層水體中的湍混合特征及其影響因子。

上層深度內，湍動能耗散率與湍混合率強度隨深度變小，這主要是因為在上層，隨著深度的增大，風應力、波浪破碎等外部作用的影響逐漸變小，另外，水體本身由于密度梯度逐漸變大而趨向穩定。為進一步揭示上層水體湍混合影響因子，本文對該層湍混合率進行垂向平均，分別與同步觀測得到的海表風應力數據、相同深度平均得到的海流數據進行交叉譜分析來探討它們之間的關聯程度。由于涉及不同量綱，因此在分析之前本文對各要素序列進行了無量綱化處理［14］。

圖9（a）是風應力與湍混合率的交叉譜分析［15］結果，圖中水平虛線表示95%的置信度，結果顯示，僅有周期為2.18h的振蕩是顯著的，其對應的落后長度譜值是－0.26，也就是說湍混合要滯后于風應力大約0.26h。海流流速與湍混合率的交叉譜分析結果（見圖9（b））揭示了2個顯著的振蕩周期，1個位于4h處，另1個位于3.4h處，相關系數在4h周期處取得最大值為0.849，對應的落后長度譜值為－0.88，即湍混合要滯后于流速大約0.88h。綜合以上結果，本文認為在觀測時段內該站點的湍混合對風應力的響應要比對流速的響應迅速。由于掌握的數據有限，本文暫不討論其它要素對湍混合的影響。

圖9 風應力與湍混合率的交叉譜分析結果（a）及流速與湍混合率的交叉譜分析結果（b）Fig.9 Crossspectrum between wind andκρ （a）and Crossspectrum between current andκρ （b）

圖8顯示的A站點下層湍耗散系數與湍混合率的分布則表明，在下層水體湍動能耗散率與湍混合率強度隨距海底高度的增加而減弱。這主要是因為隨著離底高度的增加，底摩擦對湍混合的促進作用越來越不明顯，同時水體也會由于密度梯度逐漸變大而趨向穩定。顯然，底應力是下層水體湍混合不可忽略的影響因子。下面本文將根據LADCP測流數據來估計底應力并分析底應力與湍混合的關聯程度。海洋邊界層的結構和大氣邊界層有很多類似的地方，例如，普遍認為海洋邊界層是一個對數層，即其流速隨著離海底高度的增加而呈對數規律增加。該對數層位于地球旋轉效應起主要作用的深度之下，同時又位于一個很薄的底邊界層之上。在對數層內，流速剖面可以用如下公式表示［16］：

其中：U是平均流；z是距離海底高度；κ是VonKarman常數；z0為底粗糙度；u＊為摩擦速度。確定對數層的存在非常重要，因為它提供了一種估算底應力的方法。首先根據LADCP實測流速剖面和上述對數關系式，通過流速剖面對數擬合求取z0和u＊，然后根據公式：τ＝求取底應力τ，其中：ρ為海水密度。根據以上方法，本文得出了觀測期間17個時刻的底應力的時間序列。由于在觀測的第4～6小時、第9小時和第22～25小時速度剖面沒有表現出明顯的對數曲線特征，因此，為了不引進新的誤差，本文將這8個觀測時刻的數據舍棄，只對其他17個時刻進行對數擬合。將底應力時間序列與該層湍混合率進行垂向平均后的時間序列無量綱化后進行比較，結果如圖10所示。從圖中可以明顯看出，湍混合率變化與底應力變化基本對應，底應力較大的時刻湍混合率也較大，混合較強。經統計，底應力與湍混合率的時間序列相關系數達到了0.602 1，這說明了底應力確實對該層水體的湍混合起到了重要作用。由于該站點所處位置地形復雜，可以推測，越接近海底，Thorpe尺度、湍混合率均會增加，不過這有待更深入的調查、更詳盡的資料予以分析證實。

圖10 湍混合率kρ與底應力τ的時間序列Fig.10 Timeseries of kρandτ

3 結論

本文基于舟山外海一個觀測站位（A站）周日的LADCP、CTD資料，對該站位小尺度湍混合參數進行估計，分析并討論了其時空分布特征及影響因子，得到如下結論：

（1）Thorpe尺度在垂向上呈現出明顯的分層結構，最大值可以達到11.17m。Thorpe尺度的大值均出現于水位序列的峰值附近且漲潮時的湍流翻轉明顯大于落潮時的湍流翻轉。功率譜分析表明，垂向平均的Thorpe尺度的半日潮周期最為顯著。

（2）對Brunt-Vaisala頻率的分析表明，觀測期間該站點在鉛直方向上呈現出了顯著的雙密度躍層結構。弱躍層中近慣性頻率的內波和近半日潮頻率的內潮信號最為明顯而強躍層中則表現出了明顯的高頻內波和近半日潮頻率的內潮特征。

（3）觀測期間，湍動能耗散率的平均值為2.79×10－7W/kg，量級在10－10～10－6W/kg之間變化。湍混合率的平均值為7.1×10－4m2/s，量級在10－5～10－2m2/s之間變動。

（4）湍動能耗散率與湍混合率的時空分布基本一致，均以密度躍層核心深度曲線為界呈現出明顯的上、中、下3層結構。中層水體層結最穩定，但伴有間歇性的強混合過程。下層水體湍動能耗散率與湍混合率強度則隨離底高度的增加而減弱，底應力對該層水體的湍混合起到了重要作用。

（5）上層水體，湍動能耗散率與湍混合率強度隨深度變小。交叉譜分析結果顯示，湍混合率要滯后于風應力大約0.26h，滯后于流速大約0.88h，在觀測時段內該站點的湍混合對風應力的響應要比對流速的響應迅速。

［1］吳立新，荊釗，Steve Riser，等.利用Agro浮標估計南大洋混合的時空變化 ［J］.中國基礎科學·研究進展，2012，4：20-21.

［2］Egbert G D，Ray R D.Significant dissipation of tidal energy in the deep ocean inferred from satellite altimeter data ［J］.Nature，2000，405（15）：775-778.

［3］鐘貽森.黃東海湍流混合與雙擴散現象及其季節變化 ［D］.青島：中國海洋大學海洋環境學院，2009.

［4］劉志宇.強潮驅陸架海中的湍流與混合 ［D］.青島：中國海洋大學海洋環境學院，2009.

［5］盧著敏，陳桂英，尚曉東.南海北部中深層細結構混合研究 ［J］.熱帶海洋學報，2009，28（3）：21-28.

［6］Su J L，Pan Y Q.On the shelf circulation north of Taiwan［J］.Acta Oceanol Sin，1987，6（Suppl I）：1-20.

［7］匡曉迪，郭心順，范洪濤.CTD資料預處理規范化的探討 ［J］.海洋技術，2009，28（2）：33-36.

［8］Ann Gargett And Teresa Garner.Determining Thorpe Scales from Ship-Lowered CTD Density Profiles［J］.Journal Of Atmospheric And Oceanic Technology，2008，25：1657-1670.

［9］Thorpe S A.Turbulence and mixing in a Scottish loch［J］.Phil Trans R Soc Lond A，1977，286：125-181.

［10］馮士笮，李鳳岐，李少菁.海洋科學導論［M］.北京：高等教育出版社，1980.

［11］國家技術監督局.GB12763.7-91-1992.海洋調查規范—海洋調查資料處理［S］.北京：中國標準出版社，1992.

［12］汪嘉寧，魏皓，李偉.東海內陸架春季躍層和內波影響下的環境要素分布 ［J］.海洋與湖沼，2012，43（3）：644-648.

［13］Dillon T M.Vertical overturns：a comparison of Thorpe and Ozmidov length scales ［J］.Journal of Geophysical Research，1982，87（C12）：9601-9613.

［14］張衛華，趙銘軍.指標無量綱化方法對綜合評價結果可靠性的影響極其實證分析 ［J］.統計與信息論壇，2005，20（3）：33-36.

［15］劉天然，魏皓，趙亮，等.北部灣春季季風轉換時期兩潛標站余流分析 ［J］.熱帶海洋學報，2010，29（3）：10-16.

［16］Lueck R G，Lu Y Y.The logarithmic layer in a tidal channel［J］.Contin.Shelf Res，1997，17：1785-1801.