區(qū)間線(xiàn)性系統(tǒng)的Farkas型定理

(杭州電子科技大學(xué)運(yùn)籌與控制研究所，浙江 杭州310018)

0 引 言

著名的Farkas 定理及其各種推廣形式一直被廣泛地應(yīng)用于線(xiàn)性?xún)?yōu)化和非線(xiàn)性?xún)?yōu)化問(wèn)題。近年來(lái)，越來(lái)越多的學(xué)者注重區(qū)間線(xiàn)性?xún)?yōu)化的研究，因此將Farkas 定理推廣到區(qū)間系統(tǒng)中是非常有必要的。從1989年Rohn[1]首次將Farkas 定理推廣到區(qū)間線(xiàn)性方程組的弱可行開(kāi)始，直至目前，區(qū)間線(xiàn)性系統(tǒng)(包括區(qū)間線(xiàn)性方程組和區(qū)間線(xiàn)性不等式組)的8個(gè)問(wèn)題的Farkas型充要條件都已被建立[2-4]。最近，Li等[5]提出了關(guān)于區(qū)間線(xiàn)性系統(tǒng)新的統(tǒng)一的模式，如何將Farkas 定理推廣到這個(gè)新的區(qū)間線(xiàn)性系統(tǒng)是本文將要探討的問(wèn)題。

1 若干定義和引理

記{±1}m為各分量都是{1，-1}的m-維向量的全體，令e= (1，1，…，1)T是各分量都為1的m-維向量，一個(gè)矩陣A= a()ij的絕對(duì)值是指故可得對(duì)于一個(gè)給定的向量y∈Rm，記Ty=diag(y1，y2，…，ym)為相應(yīng)的對(duì)角矩陣。對(duì)每一個(gè)x∈Rn，記它的符號(hào)向量為sgn x，定義為:這里i=1，2，…，n。因此得到這里z=sgn x∈{±1}n。給定一個(gè)區(qū)間矩陣AΙ=[Ac-AΔ，Ac+AΔ]，對(duì)于任意的向量y ∈Rm和z∈Rn，定義矩陣:Ayz=Ac-TyAΔTz。類(lèi)似的，對(duì)于一個(gè)區(qū)間向量bΙ=[bc-bΔ，bc+bΔ]以及任意向量y∈{±1}m，定義向量:by=bc

設(shè)ΙRm×n是一個(gè)m×n的區(qū)間矩陣，IRm是一個(gè)m-維的區(qū)間向量，令A(yù)Ι∈IRm×n，bΙ∈IRm。一個(gè)區(qū)間線(xiàn)性系統(tǒng)如下:

它表示下列線(xiàn)性方程的集合:

其中，A和b 滿(mǎn)足:

如果存在A和b 滿(mǎn)足條件式(3)并且使式(2)是可解的(或可行的，即式(2)有一個(gè)非負(fù)解)，那么就稱(chēng)區(qū)間系統(tǒng)(1)是弱可解(或弱可行)。如果對(duì)任意滿(mǎn)足條件式(3)的A和b 都能夠使得式(2)是可解的(或可行的)，那么稱(chēng)區(qū)間系統(tǒng)(1)是強(qiáng)可解(或強(qiáng)可行)。用同樣的方法可以定義出區(qū)間線(xiàn)性不等式組的弱可解(或弱可行)和強(qiáng)可解(或強(qiáng)可行)。

如果對(duì)任意的b∈bΙ都存在A∈AΙ使得式(2)可解(或可行)，那么就稱(chēng)區(qū)間線(xiàn)性系統(tǒng)(1)是 (bI)-強(qiáng)可解(或強(qiáng)可行)。類(lèi)似地，可以定義出區(qū)間線(xiàn)性不等式組AΙx≤bΙ的(bI)-強(qiáng)可解(或強(qiáng)可行)[5]。

下面幾個(gè)關(guān)于區(qū)間線(xiàn)性系統(tǒng)弱可解和弱可行的Farkas型定理被用來(lái)獲得接下來(lái)一節(jié)中的主要結(jié)果[5]。

引理1系統(tǒng)AΙx=bΙ是弱可行的當(dāng)且僅當(dāng) (?p)(AΤp≥0，?A∈AΙ?bΤp≥0，?b∈bΙ)。

引理2系統(tǒng)AΙx≤bΙ是弱可行的當(dāng)且僅當(dāng) (?p≥0)(AΤp≥0，?A∈AΙ?bTp≥0，?b∈bΙ)。

引理3系統(tǒng)AΙx≤bΙ是弱可解的當(dāng)且僅當(dāng)(?z∈{±1}n)(?p≥0)((Aez)Τp=0?bΤp≥0，?b∈bΙ)。

引理4系統(tǒng)AΙx≤bΙ是弱可解的當(dāng)且僅當(dāng)

2 主要結(jié)果

本節(jié)的主要目的是給出區(qū)間線(xiàn)性方程組的(bI)-強(qiáng)可行，以及區(qū)間線(xiàn)性不等式組的(bI)-強(qiáng)可解和(bI)-強(qiáng)可行的Farkas型充要條件。

定理1 區(qū)間線(xiàn)性系統(tǒng)AΙx=bΙ是 (bI)-強(qiáng)可行的當(dāng)且僅當(dāng):

證明 必要性。令A(yù)Ιx=bΙ是 (bI)-強(qiáng)可行的，因此對(duì)任意的b∈bΙ都存在A0∈AΙ使得方程A0x=b 有非負(fù)解。如果向量p 滿(mǎn)足對(duì)任意的A∈AΙ都有ATp≥0，則表示A0Tp≥0。因此對(duì)任意的b∈bΙ都有bΤp= (A0x)Τp=xΤA0Τp≥0。

充分性。令式(4)成立。假設(shè)該區(qū)間系統(tǒng)AΙx =bΙ不是 (bI)-強(qiáng)可行的，則表示存在b0∈bΙ使得對(duì)任意的A ∈AI方程Ax=b0都沒(méi)有非負(fù)解，即AΙx=b0不是弱可行的。所以由引理1 得(?p)(AΤp≥0，?A∈AΙ?b0Τp＜0)，該式等價(jià)于:

顯然，式(5)與式(4)矛盾。因此，系統(tǒng)AΙx=bΙ是 (bI)-強(qiáng)可行的。

定理2 區(qū)間線(xiàn)性系統(tǒng)AΙx≤bΙ是 (bI)-強(qiáng)可行的當(dāng)且僅當(dāng):

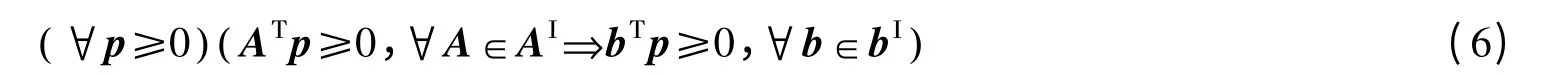
證明 必要性。令A(yù)Ιx≤bΙ是 (bI)-強(qiáng)可行的，則對(duì)于任意的b∈bΙ都存在A0∈AΙ使得不等式A0x≤b 有非負(fù)解。如果向量p≥0 滿(mǎn)足:對(duì)任意的A∈AΙ都有ATp≥0，則表示A0Tp≥0。因此，對(duì)任意的b∈bΙ有bΤp≥ (A0x)Τp=xΤA0Τp≥0。

充分性。類(lèi)似于定理1 充分性的證明，采用反證法，再應(yīng)用引理2 即可得證。

定理3 區(qū)間線(xiàn)性系統(tǒng)AΙx≤bΙ是 (bI)-強(qiáng)可解的當(dāng)且僅當(dāng)

證明 必要性。令A(yù)Ιx≤bΙ是 (bI)-強(qiáng)可解的。假設(shè)式(7)不成立，則有:

由于向量p的非負(fù)性，所以bΤp ＜0 則意味著bΤp ＜0，從而由式(8)得:

由引理3 知式(9)是系統(tǒng)AΙx≤不是弱可解的Farkas型充要條件，即由式(9)可知，AΙx≤不是弱可解。即存在b∈bΙ使得對(duì)任意的A∈AΙ不等式Ax≤b 都沒(méi)有解，因此由定義知系統(tǒng)AΙx≤bΙ不是(bI)-強(qiáng)可解的，矛盾。所以，式(7)成立。

充分性。類(lèi)似于定理1 充分性的證明，采用反證法，再應(yīng)用引理3 即可得證。

接下來(lái)，給出上述3種情況另一種形式的Farkas型定理，顯然對(duì)應(yīng)同一種情況的Farkas型條件之間是等價(jià)的。

定理4 區(qū)間線(xiàn)性系統(tǒng)AΙx=bΙ是 (bI)-強(qiáng)可行的當(dāng)且僅當(dāng)

證明 由定理1可知只需要證明條件(4)成立當(dāng)且僅當(dāng)條件(10)成立。

充分性。令式(10)成立。如果向量p 滿(mǎn)足，對(duì)任意的A∈AΙ都有AΤp≥0，則 (Aze)Τp≥0，這里z=sgn p，展開(kāi)后得即所以由式(10)得到因此對(duì)任意的b∈bΙ都有得證。

定理5 區(qū)間線(xiàn)性系統(tǒng)AΙx≤bΙ是 (bI)-強(qiáng)可行的當(dāng)且僅當(dāng)

定理6 區(qū)間線(xiàn)性系統(tǒng)AΙx≤bΙ是 (bI)-強(qiáng)可解的當(dāng)且僅當(dāng)

證明 必要性。類(lèi)似于定理1 充分性的證明，采用反證法，再應(yīng)用引理4 即得證。

充分性。類(lèi)似于定理4 充分性的證明，再應(yīng)用定理3 即可得證。

3 結(jié)束語(yǔ)

本文給出了區(qū)間線(xiàn)性系統(tǒng)的3種Farkas型定理，為進(jìn)一步研究區(qū)間系統(tǒng)和區(qū)間優(yōu)化提供了理論基礎(chǔ)。對(duì)區(qū)間系統(tǒng)而言，(bI)-強(qiáng)問(wèn)題總共分為等式的(bI)-強(qiáng)可解、(bI)-強(qiáng)可行、不等式的(bI)-強(qiáng)可解和(bI)-強(qiáng)可行4種情況[5]。而本文只描述了后3種情況的Farkas型充要條件，關(guān)于區(qū)間線(xiàn)性方程組的(bI)-強(qiáng)可解的簡(jiǎn)潔實(shí)用的Farkas型充要條件還未建立，這也是一個(gè)可以繼續(xù)深入研究的問(wèn)題。另外，區(qū)間優(yōu)化問(wèn)題的研究有了長(zhǎng)足的發(fā)展，比如文獻(xiàn)[7]。如何將區(qū)間系統(tǒng)的Farkas型定理應(yīng)用到這些優(yōu)化問(wèn)題中去研究解的特性，是一個(gè)很有趣的課題。

[1]Rohn J.A Farkas-type theorem for linear interval equations[J].Computing，1989，43(1):93-95.

[2]Karademir S，Prokopyev O A.A short note on solvability of systems of interval linear equations.Linear Multilinear Algebra[J].Linear and Multilinear Algebra，2011，59:(6)707-710.

[3]Rohn J.A Farkas-type theorem for interval linear inequalities[J].Optimization Letters，2014，8(4):1 591-1 598.

[4]Xia M，Li W，Li H.Farkas-type theorems for interval linear systems[J].Linear and Multilinear Algebra，2015，63(7):1 390-1 400.

[5]Li H，Luo J，Wang Q.Solvability and feasibility of interval linear equations and Inequalities[J].linear Algebra and its Applications，2014，463:78-94.

[6]Fiedler M，Nedoma J，Ramík J，et al.Linear Optimization Problems with Inexact Data[M].New York:Springer，2006:35-77.

[7]Luo J，Li W.Strong optimal solutions of interval linear programming[J].Linear Algebra and its Applications，2013，439(8):2 479-2 493.