《數學分析》中的分析與綜合方法研究

鄒健，宋述剛，陳忠 （長江大學信息與數學學院，湖北 荊州434023）

分析與綜合是歷史唯物主義與辯證唯物主義的基本思維方法之一，也是形式邏輯的方法之一［1］。按照哲學的觀點，分析是把整體事物分解為各個部分、方面、階段或要素，用相對靜止、孤立的觀點逐個加以研究的思維方法。分析即為化整為零。分析方法是多種多樣的，有定性分析、定量分析、因果分析、結構分析、功能分析等。而綜合則是在分析的基礎上，將事物各個部分有機整合的思維方法。綜合即為積零為整。這種整合，不是簡單的、機械的部分相加，而是把思維對象的各個方面按其內在聯系有機結合為一個統一的整體，從而把握事物的宏觀本質的性質。

分析與綜合雖然是2種不同的思維方法，但它們象一對孿生兄弟一樣，形影相隨，相互依賴，相互影響與轉化。首先，分析是綜合的前提和基礎，沒有系統、全面、科學的分析，就不可能有正確的綜合。其次，分析離不開綜合的指導，分析以綜合為目的，綜合是分析的完成。分析與綜合的思維過程是從感性具體到思維抽象，再從思維抽象到客觀具體的過程。一般的，前者多用分析法，后者多用綜合法。

《數學分析》的主要內容是微積分理論，其創立者是英國科學家牛頓與德國科學家萊布尼茲［2，3］。微積分的創立是人類文明史上的一個里程碑，其理論在18、19世紀得到了極大的發展，形成了分析數學的基礎理論，并在物理學、化學、天文學、生物學等自然科學與工程技術中有著廣泛的重要應用。在大學非數學專業中，關于微積分的課程被稱為《高等數學》，但在數學專業中，則稱為《數學分析》，這表明《數學分析》更著重強調微積分的分析綜合思想方法。

雖然微積分研究的對象是函數，但其研究的課題涉及到無窮的世界，包括無窮集合、無窮過程等，如實數集、無窮數列、無窮級數、數列極限、函數極限、函數的導數與積分等。在《數學分析》中，有窮與無窮是一對典型的相互對立統一的矛盾。有窮中包含著無窮，而無窮更是包含著有窮，它們在一定的條件之下可以相互轉化。例如，有窮區間（0，1）包含了無窮多個點，無窮區間（0，＋∞）包含了無窮多個有窮區間；在變換y＝tanx之下，兩者相互轉化。

人類對無窮的認識，經歷了一個艱難、漫長的過程。第1次數學危機（無理數危機）、第2次數學危機（無窮小量危機）、第3次數學危機（無窮集合悖論）都與對無窮的認識有關。無窮的世界千姿萬態，充滿了難以想象的奧秘。這是因為人的認識、思維過程乃至生命都是有限的。如何運用有限的思維過程去認識、把握無限的集合與變化過程？適當的方式就是化無窮為有窮、化復雜為簡單，這就需要運用分析與綜合方法。

下面，筆者以《數學分析》課程中極限和定積分這2個重要概念為例，探討其中的分析與綜合方法。

1 極限概念中的分析與綜合方法

極限理論是《數學分析》的基礎與工具，而數列極限又是極限論的基本概念。這里，筆者僅以數列極限的概念為例，探討其中的分析與綜合方法。考慮數列極限：

其定性的定義為：當n趨近于無窮大時，an無限趨近于a。如何尋求其定量的定義呢？事實上，an趨近于a是一個無窮的復雜過程，運用分析的方法，可以把它分解為各個變化階段，如：

對于進入每個變化階段，可以用相對靜止、孤立的觀點研究它們需要具備什么樣的條件。以具體的極限＝0為例，要求：

所得條件是自變量n必須分別大于某個正整數N＝10，N＝100，N＝500。這成為每個變化階段所具備的共性，即可以綜合為：對于給定的任意小的正數，總存在一個正整數，使得數列的項數大于這個正整數時，數列的變化進入相應的階段。

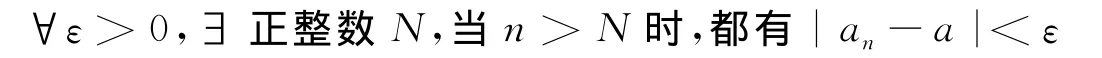
正是運用了分析與綜合的方法，德國著名數學家魏爾斯特拉斯才首次給出了極限的現代定義。

運用同樣的思維方法，可以得到函數極限的定義。以此為基礎，又可定義函數連續的概念與導數的概念。

2 定積分概念中的分析與綜合方法

首先，使用分析法，將曲邊梯形用鉛錘的直線分割成若干個小的窄曲邊梯形，然后對每個小曲邊梯形，用孤立、靜止的觀點處理，將其近似看著小矩形，即函數f（x）在每個小區間［xi－1，xi］上看作是不變的，其值可任取f（ξi），ξi∈ ［xi－1，xi］。于是第i個小曲邊梯形面積近似值為f（ξi）Δxi（Δxi＝xi－xi－1）。

其次，使用綜合法，將各小曲邊梯形面積近似值相加，得到整個曲邊梯形面積的近似值：

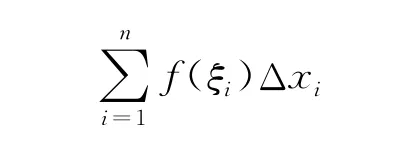
但這僅僅是一個近似值，需要有機整合。不難發現，隨著分割越來越細密，和式（ξi）Δxi的近似程度就越高。因此，有機整合的手段就是讓分割T越來越細密，當分割的細度 ‖T‖ →0時，和式的極限（如果存在的話）就是該曲邊梯形的面積（精確值）。經過抽象概括，即得定積分的定義：

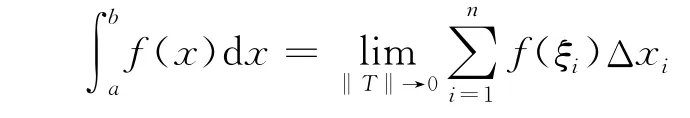
由此可知，在定積分的定義中，分割、近似即為分析過程，作和、取極限則為綜合過程。可以說，定積分的定義是分析法與綜合法相結合的完美范例。

運用同樣的思維方法，可以定義重積分、曲線積分、曲面積分等概念。

3 結語

《數學分析》現已成為現代分析數學（包括函數論、泛函分析、微分方程等學科）的重要基礎，因而學好該課程就顯得尤為重要。由于大學與中學數學教學的差異與銜接等問題，導致相對一部分大學新生往往不能適應《數學分析》的學習，特別是感到基本概念難于理解，思維方式與表達形式不易掌握。因此，對《數學分析》課程中基本概念與思維方式教學的探討就顯得十分重要。極限、導數、積分等概念是《數學分析》中至關重要的基本概念，對它們的理解與掌握，是學好該課程的關鍵所在。而對這些概念的認識，又恰好是教學的重點與難點。由上所述，當了解了導入這些概念的分析與綜合的思想方法以后，化解難點、突出重點就變得迎刃而解了。當然，除了上述探討的分析與綜合思維方法以外，《數學分析》中還蘊含客觀世界普遍聯系與運動、發展的觀念，人類認識與實踐的觀念與規律，唯物辯證法的基本發展規律如質量互變規律、對立統一規律、否定之否定規律等等［4］。因此，在《數學分析》教學中，注重相關的哲學思想與方法，可以提升教師與學生雙方的認識高度與水平，真正培養學生發現問題、分析問題、解決問題的能力，對指導《數學分析》及其相關后繼課程的教學，提高教學質量，都有十分重要的意義。

［1］李秀林，王于，李懷春 .辯證唯物主義和歷史唯物主義原理 ［M］.第5版，北京：中國人民大學出版社，2004.

［2］華東師大數學系 .數學分析 ［M］.第4版 .北京：高等教育出版社，2010.

［3］徐利治 .數學方法論選講 ［M］.第3版 .武漢：華中科技大學出版社，2000.

［4］張景中 .數學哲學 ［M］.北京：北京師范大學出版社，2010.