基于星模擬器綜合誤差的星點修正方法的研究
王小龍,張國玉,2,3,孫高飛,2,3,張健 ,張建良
(1.長春理工大學,長春 130022;2.光電測控與光電信息傳輸技術教育部重點實驗室,長春 130022;3.吉林省光電測控儀器工程技術研究中心,長春 130022;4.長春航空航天大學,長春 130022)
隨著航天技術的迅猛發展,星模擬器作為星敏感器的地面標定測試設備,也要求其具有較高的精確度。但由于星模擬器綜合誤差的存在使得顯示星點位置計算后的星間位置與理論星間位置存在差異,影響仿真精度,本文提出一種基于星模擬器綜合誤差的星點位置修正方法,適用于任意靜態星模擬器光學系統的星點位置修正,以進一步提高星模擬器模擬精度。
1 靜態星模擬器工作原理
靜態星模擬器主要由準直系統、星點分劃板組件、濾光片組件、光源、電源和安裝支架等組成。工作原理如圖1所示。光源發出的亮度均勻的光線,經過濾光片后照射到位于準直物鏡焦平面的星點板上,通過星點板上的透光微孔形成模擬星點,模擬星點產生的光線經過準直物鏡準直后成為平行光射出,實現了對星圖的模擬。

圖1 靜態星模擬器原理圖
2 星點位置修正方法
星點板是靜態星模擬器的顯示器件,其星點的位置決定了星模擬器的模擬精度。星間角距計算原理如圖2所示,圖中YOX平面相當于星點板,A、B為星點板上任意兩點,θ為點A、B之間的星間角距f0為準直物鏡的焦距,O為光軸與星點板中心的交點。
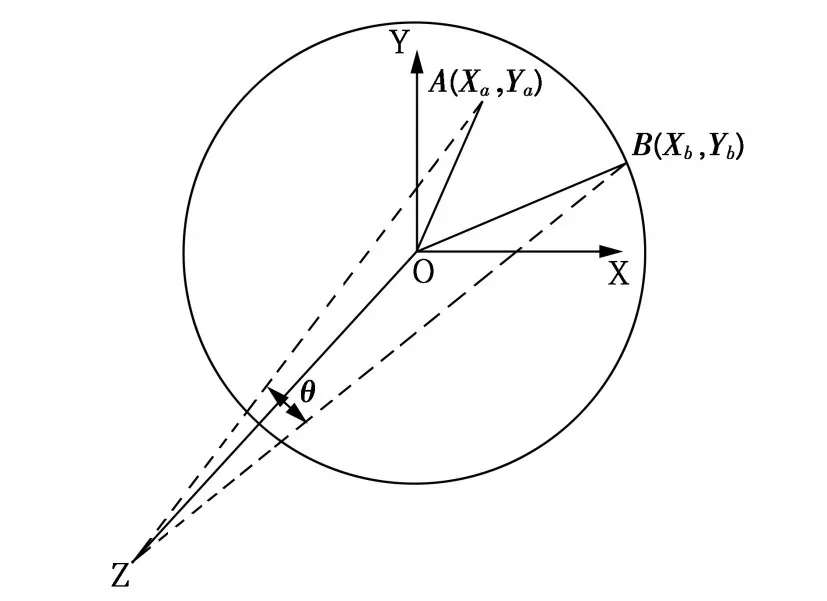
圖2 星間角距計算原理圖
實際測試過程中可以測得任意A、B兩點的方位值與俯仰值,得到兩點A(α1,β1),B(α2,β2),由公式(1)計算求得:
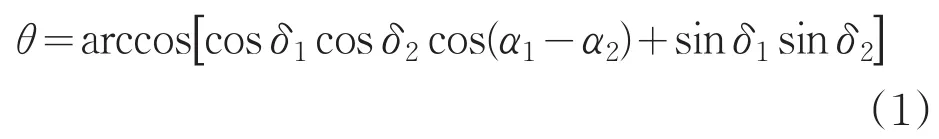
實際星間角距測量值與理論值的差值即為任意兩點的星間角距誤差。若其中一點為中心星點時,即為另一星點的單星位置誤差。
星點位置刻劃時需要知道當前系統的焦距f,f的準確性直接影響星模擬器的模擬精度,因此用經緯儀對中心點附近的星點D(xd,yd)進行反復測量,其中x,y分別為星點在分劃板上相對于中心點的坐標,反復測試星點的方位和俯仰值,通過公式(1),(2),(3)即可求得光學系統實際焦距f。
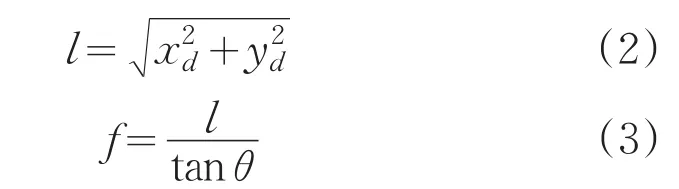
式中,l為D點到中心點的距離;θ為D點與中心點角距值。
不同光學系統成像質量存在差異,而且成像質量與視場相關,故無法僅通過修正一個焦距值就使得全部星點的單星位置誤差達到≤10″的精度。故為了進一步提高模擬精度,需要對各個星點進行進一步修正。
將實測星點R(xr,yr)的實測角距值θ帶入到公式(2),公式(3)中,其中xr,yr為R點的在分劃板上的坐標值,得到R點對應的焦距f′。如圖3和圖4所示,將實際角度值與理論角度值進行比較即可得出R點在徑向的修正值。其中α為理論角度值,α′為實測角度值,l為R點與中心點的實際距離,Δl為R點徑向移動的距離。
將Δl和R點在星點板上的坐標R(xr,yr)帶入公式(4)可以得到R點在星點板上新的位置R(x′r,y′r),完成對單星位置誤差的修正。

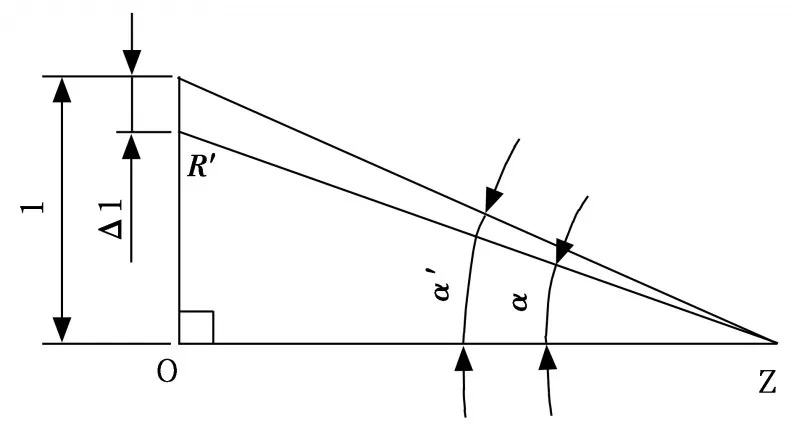
圖3 ROZ平面單星位置誤差與星點刻劃位置的修正量關系圖
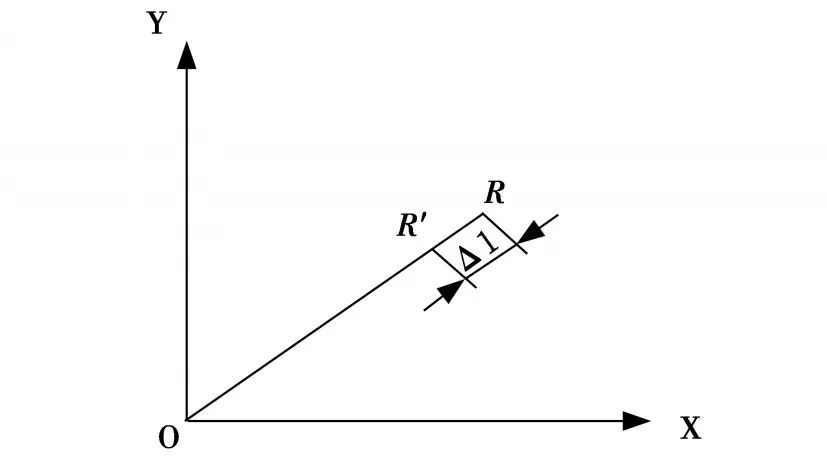
圖4 YOX平面單星位置誤差與星點刻劃位置與修正量關系圖

圖5 新坐標系示意圖
通過建立以觀測點為原點,x軸,y軸與XOY坐標系相應坐標軸平行的坐標系X′O′Y′對上述修正方法進行驗證,坐標系X′O′Y′如圖5所示。設以分劃板上的星點與坐標系原點為兩個端點的向量坐A、B與坐標原點構成的向量為,通過幾何關系計算可得到兩向量之間的夾角,其公式如式(5)所示。由式(5)計算的值與理論值相比較,可以達到對修正方法檢驗的目的。標為(x,y,f),其中x,y為修正后星點的位置坐標值,f為對應星點的焦距值,則任意兩個星點

由于上述方法對各個視場星點修正時使用了不同的焦距值,相當于修正的星點不在同一平面上但之間是相互平行。由于星點刻劃面是一個平面,故需要對各個視場的星點的焦距進行歸一化處理,計算得出修正后的星點在星點分劃面上的刻劃位置。
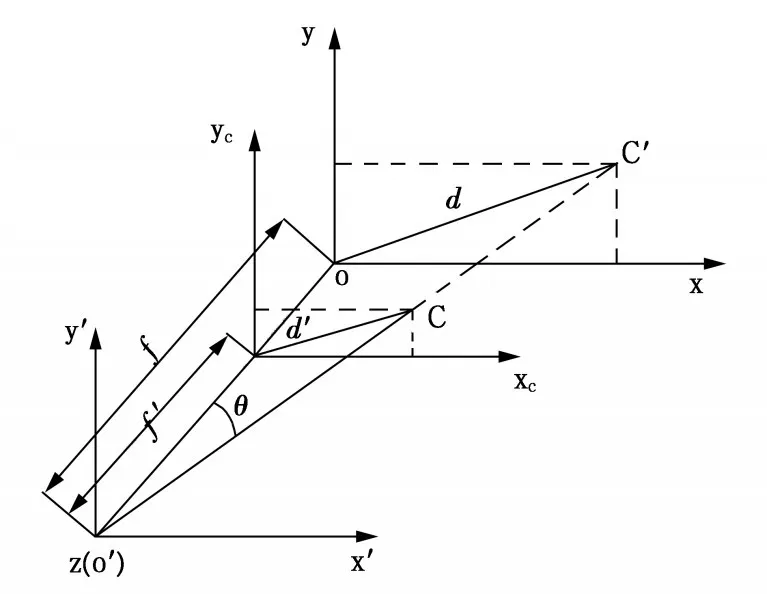
圖6 修正量關系示意圖
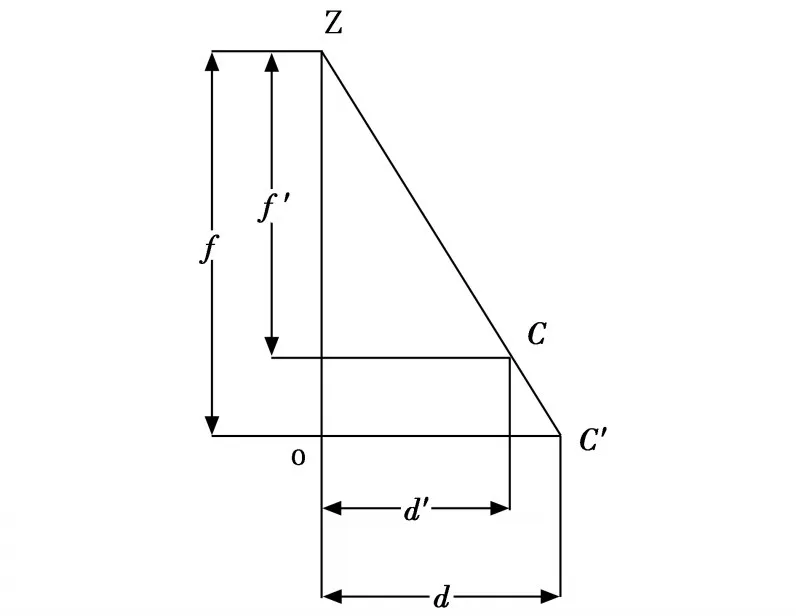
圖7 ZOC平面示意圖
星點刻劃位置推導如圖6和圖7所示。圖中C為任意星點,其坐標為(xc,yc);f為實際擬定焦距;f′為邊緣點焦距;d為星點到中心點的距離;d′為星點在焦距f′下到中心點的距離。由于光學系統中心視場像差小,成像質量好,故可近似使用中心視場焦距f作為星點板位置刻劃焦距。可根據三角形幾何關系,通過計算得出新的星點位置即在星點板上的位置,從而完成新星點板刻劃,實現對全部星點在星點板上的位置誤差修正。
3 修正過程與結果
本文以一個15點的星圖為例,用經緯儀對原星點板中的15個星點進行觀測,測得數據按照上一節所敘述的方法進行單星位置誤差的修正。將修正后重新刻劃的星點板再次進行觀測,測得數據與修正前的實測值和理論值比較,可以清晰的看出修正過程中對單星位置誤差模擬精度的進一步提高,15點星圖如圖8所示。其測試數據如表1。
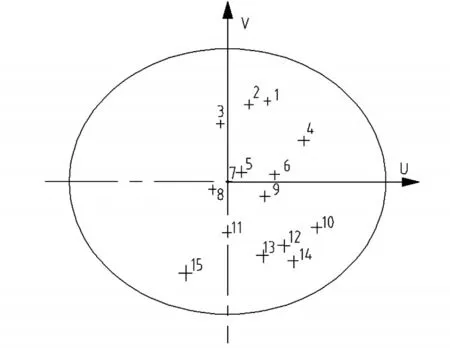
圖8 星點分劃板星點位置圖
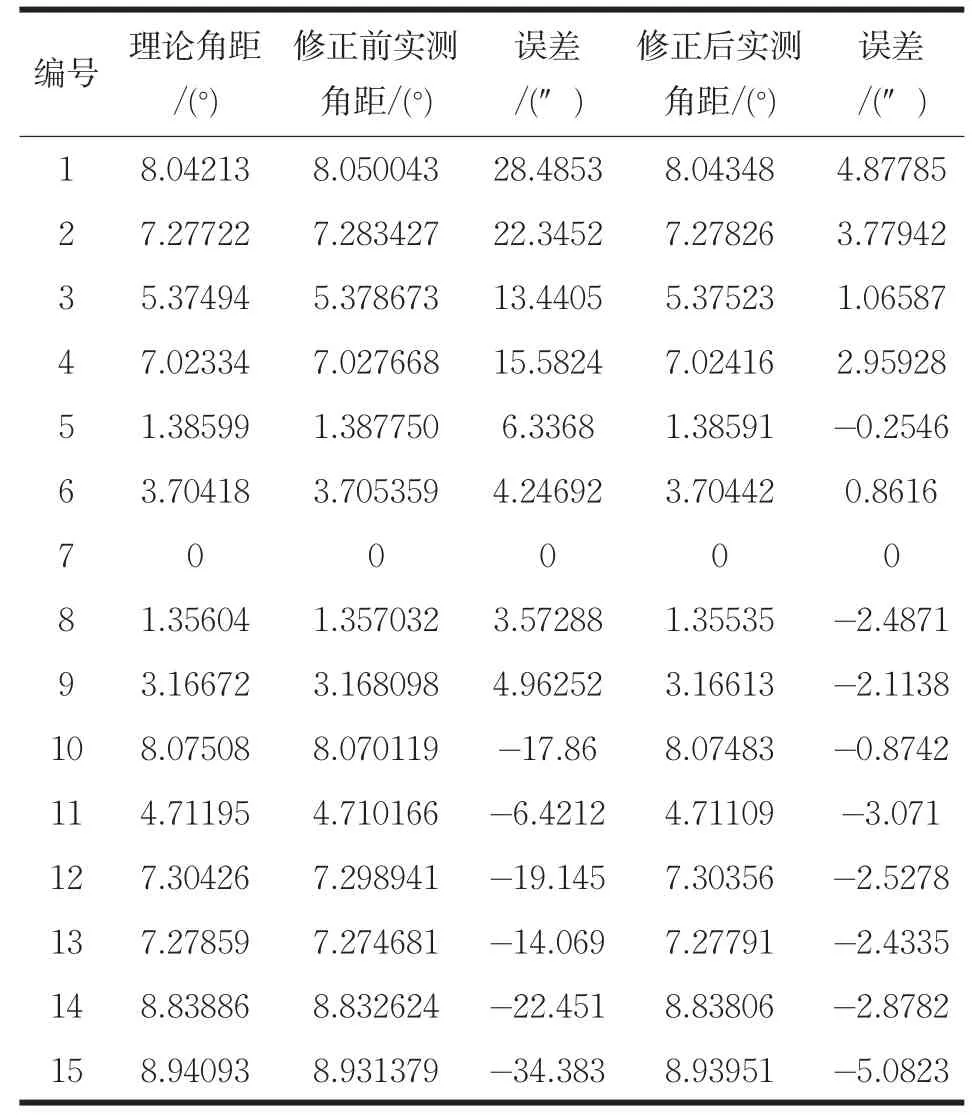
表1 單星位置誤差表
根據表中的修正前后數據的誤差對比,修正后的各點誤差全部滿足小于±10″的要求。利用上述修正方法有效地減小焦距誤差、光學系統像差以及裝配誤差對單星星點位置誤差的綜合影響,有效提高了星模擬器的模擬精度。
4 結論
本文針對靜態星模擬器的星點位置誤差提出了一種有效的修正方法來進一步提高星模擬器精度。經過理論分析與實際測量證明了該方法的可行性,對進一步提高靜態態星模擬器星點位置仿真精度具有一定的現實意義。
[1]孫高飛,張國玉,鄭茹,等.星敏感器標定方法的研究現狀與發展趨勢[J].長春理工大學學報:自然科學版,2010,33(4):8-14.
[2]郝允慧,張國玉.小型靜態星模擬器光學系統設計[J].長春理工大學學報:自然科學版,2009,32(4):45-46.
[3]孫高飛,張國玉,高玉軍,等.星敏感器地面標定設備設計[J].紅外與激光工程,2013,42(10):2822-2827.
[4]孫高飛,張國玉,王凌云,等.甚高精度星模擬器星圖顯示與控制系統研究[J].空間科學學報,2013,33(3):308-312.
[5]李春艷,李懷鋒,孫才紅.高精度星敏感器天文標定方法及觀測分析[J].光學精密工程,2006,14(4):558-563.
[6]王俁,張國玉,高玉軍,等.基于TFT-LCD的動態星模擬器星點位置修正方法[J].中國光學,2011,4(3):247-251.
[7]劉一武,陳義慶.星敏感器測量模型及其在衛星姿態確定系統中的應用[J].宇航學報,2003(3):10-16.
[8]李春艷,李懷鋒,孫才紅.高精度星敏感器天文標定方法及觀測分析[J].光學精密工程,2006,14(4):558-563.
[9]王安國.現代天文導航及其關鍵技術[J].電子學報,2007,35(12):26-28.
[10]刑飛,武延鵬,董瑛,等.微型星敏感器實驗室測試系統研究[J].光學技術,2004,30(6):703-709.

