大坡度海底管道強度分析

王博雅，康 莊，宋儒鑫，曹先凡，劉振紋

(1.哈爾濱工程大學船舶工程學院深海工程技術研究中心，黑龍江 哈爾濱 150001； 2.中國石油集團工程技術研究院，中國石油天然氣集團海洋工程重點實驗室，天津 300451)

大坡度海底管道強度分析

王博雅1，康 莊1，宋儒鑫1，曹先凡2，劉振紋2

(1.哈爾濱工程大學船舶工程學院深海工程技術研究中心，黑龍江 哈爾濱 150001； 2.中國石油集團工程技術研究院，中國石油天然氣集團海洋工程重點實驗室，天津 300451)

大坡度海底管道是油氣開發經常使用的類型。針對中國南海海底地形，研究大坡度海底管道的強度，提出工程優化方法。通過分析管道結構的受力控制方程，得到管道受力分析的主要影響參數。使用非線性時域軟件分析得到斜坡頂端和底端的管道易發生強度破壞。提出工程優化方案，頂端使用托管架和挖溝措施進行優化，底端使用懸鏈線理論進行優化設計。分析結果表明，應用優化措施后，大坡度海底管道強度滿足規范要求。

海底管道；大坡度；強度分析；工程優化方法

0 引 言

海底管道是海洋油氣資源開發的生命線，對海底石油和天然氣的生產和外輸起著關鍵性的作用[1]。大坡度海底管道是鋪設在有較大斜坡角存在的海底斜坡上的管道。目前已有的海底管道在位穩定性設計規范(如挪威船級社DNV-RP-F109)考慮的都是平坦海底的情況。但是由于斜坡角的存在，斜坡的地質不穩定性均使得大斜坡上鋪設的海底管道更容易發生屈曲、壓潰、失穩等現象，較之鋪設在平坦海底的管道在強度和穩定性方面存在著更為復雜的問題[2]。

有限元軟件如ANSYS可以對大坡度海底管道結構進行分析，但其計算動態性能差，效率低。本文對實際海洋工況中的大坡度海底管道采用非線性動力分析軟件OrcaFlex進行分析，考慮流-管相互作用對大斜坡管道強度的影響，評估計算大斜坡的地質不穩定性對管道強度和在位穩定性的影響[3]，通過校核管道強度來調整管道參數的設計，為選擇最安全、經濟的工程施工方案提供參考[4]。

1 管道力學分析

選取大地坐標系，海平面為z軸參考零點，基于小變形梁控制方程，得出管道受力方程。其中，水平運動控制方程為[5]

(1)

式中：EI為管道抗彎剛度；Teff為管道軸向張力；fr為單位長度管道重量；fzs為作用于單位長度管道的垂向載荷；mr+mc+ma-r+ma-c為單位長度管道質量、液體質量、管道和內液附加質量的總和；fxs來自波浪流載荷的莫里森方程[6]，

垂向運動控制方程為[5]

(2)

式中：V為管道所受剪力[5]，

(3)

管道計算時采用的非線性軟件基于集中質量法，在分析過程中，其求解精度隨管道參數接近運動控制方程式(1)和式(2)中參數的程度而增加[7]。

2 強度計算及結果分析

大坡度管道的總體強度分析主要內容包括：確保管道的設計滿足規范要求，所有工況(包括運營工況、水壓測試)滿足載荷的強度要求。

2.1規范要求

由于建立模型所設定的管道所用材料為X65鋼，根據美國石油協會(API)規范，在作業條件下的許用應力系數是0.8，則在整個模型的受力模擬分析過程中，管線可承受的應力最大值為358.54MPa。

2.2參數設計

設計海底管線總長9.36km，管道結構參數如下：材料為X65鋼，密度為7850kg/m3，彈性楊氏模量為207GPa，泊松比為0.30，線性膨脹系數為11.6×10-6K-1，導熱系數為45W/(m·K)，最小屈服強度為450MPa，最小拉伸強度為535MPa。根據不同水深，設計海底管道分為四部分，具體參數如表1所示。其外涂層為三層聚丙烯防腐涂層。

計算水深范圍為12～1000m，海底坡度均勻變化，最大坡度25°。海流特殊系數γ為1.9，海水密度為1.025×103kg/m3，海水溫度10℃。計算表2所示兩種工況下的管線強度。由于水深較大，因此不考慮表面波浪對管道的影響，只考慮海底海流對海底管道的影響。海底流速隨水深的變化而變化，具體值如表3所示。海床及管線鋪設位置如圖1所示。

圖1 大坡度海床及管線鋪設位置Fig.1 Large slope seabed and pipeline

管段海水深度/m管道長度/m管道直徑/英寸管道壁厚/mm11220001822．2212～3006861822．23300～5005731823．84500～8006101825．45800～10004911827．06>100050001827．0

注：1英寸=2.54 cm。

表2 大坡度海底管道兩種計算工況

表3 不同水深的海底流速

2.3 計算結果及分析

根據管道基本數據，使用OrcaFlex軟件建立大坡度海底管道模型。由于管道距海平面較遠，不考慮風浪影響，只考慮海流影響。海底海流速度穩定，不隨時間變化而變化。在用OrcaFlex動態分析管道受力時，設置100 s為動態分析總時長，時間步長為0.1 s，用以模擬海流的動態流動過程，此動態過程對管道強度會有一定影響。具體計算結果如圖2、圖3和表4所示，其中，管長為0表示管線頂端。

圖2 最大等效應力曲線Fig.2 Maximum equivalent stress

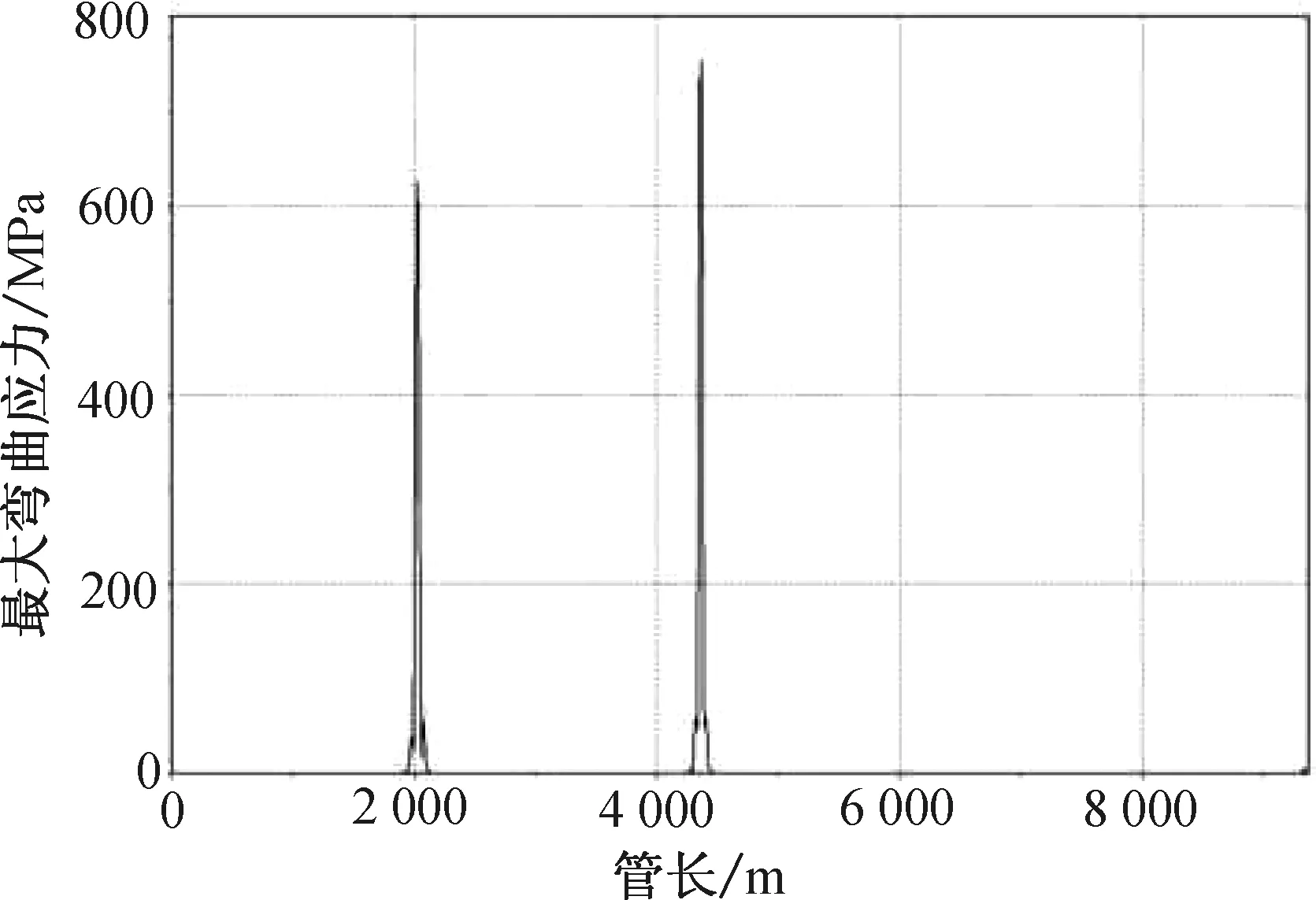
圖3 最大彎曲應力曲線Fig.3 Maximum bending stress

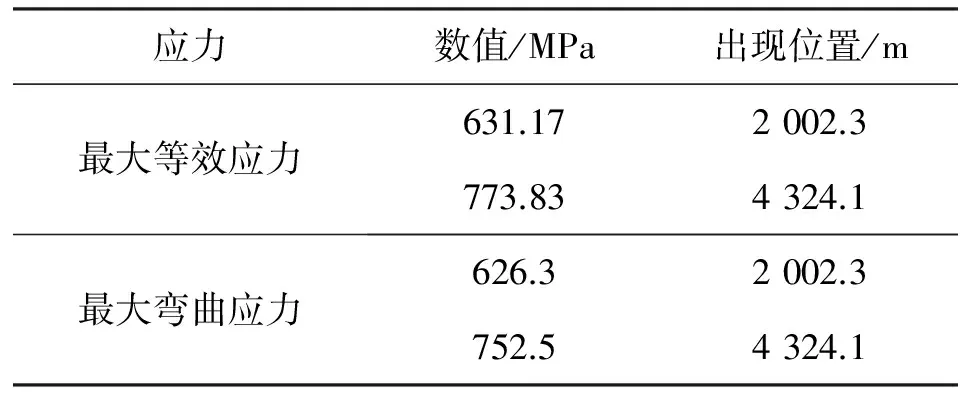
應力數值/MPa出現位置/m最大等效應力631．172002．3773．834324．1最大彎曲應力626．32002．3752．54324．1

由表4可知，等效應力最大值為773.83 MPa，大于358.54 MPa，不符合規范要求。管線長度2 002.3 m和4 324.1 m分別位于斜坡頂端和底端。兩處由于坡角存在，曲率較大，導致最大彎曲應力和最大等效應力不符合規范要求。

為使管道強度符合標準，應分別對斜坡頂端和底端采取相應的工程優化措施。

3 斜坡頂端優化措施

針對斜坡頂端，為有效減小斜坡頂端曲率，可采用建立托管架和挖溝兩種形式進行優化。

3.1托管架

托管架可以避免海底管道與海崖不平處的直接接觸，有效減小斜坡頂端曲率[8]，同時也可以達到防止大坡度海底管道受到破壞的目的。

托管架本身的強度、穩定性等需要另行設計分析，不屬于本文研究內容。設計時需要注意的是托管架的尺寸不能太大，否則安裝難度及費用會變得很大[9]。托管架的支撐靠托輥實現，屬于離散接觸支撐，管線有可能脫離托管架，同時在支撐處會導致局部彎矩的出現；另外，由于管線自重很大，托管架結構可能因管線的接觸壓力導致自身破壞。因此，在托管架設計中，應加入以下兩個因素：托管架的長度以及托管架自身結構系統選擇[10]。

設計托管架結構選擇分段桁架式。各段之間通過鉸接連接，通過調整各段之間的相對角度可以實現一定范圍內的半徑變化。

使用OrcaFlex設置托管架。本文中托管架設計成三個部分，托管架一端與斜坡頂部相切，另一端切線延長線與斜坡平行，保證管線在托管架與海床之間平穩過渡。在OrcaFlex中，通過斜坡角度及托管架位置計算托管架的長度及曲率。通過計算得到，托管架總長度為3.27m，寬6m，高8m，曲率約為0.0036m-1。托管架具體設計參數如表5所示。托管架效果如圖4所示。

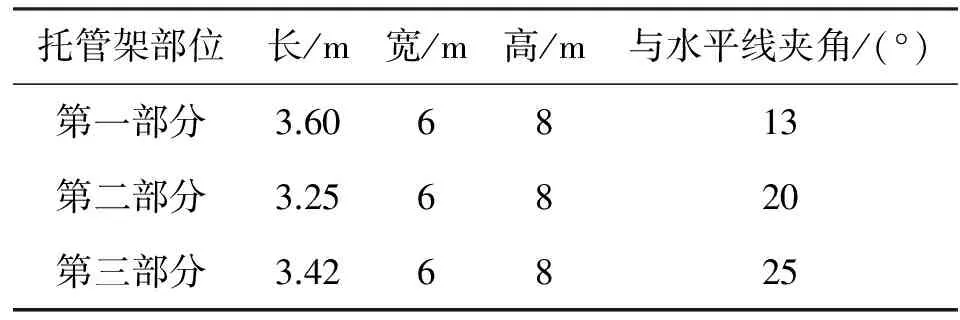
表5 托管架設計參數

圖4 托管架示意圖Fig.4 Stinger design sketch

進行動態模擬時，設置托管架剛度為800 MPa，管線會自動鋪設在托管架上。由于水深較深，托管架鋪設難度較大，而且托管架的尺寸較大不利于工程鋪設，所以工程上建議采用挖溝形式減小斜坡曲率。

3.2 挖溝

挖溝是廣泛應用于海底管道的方法，然而土壤越硬挖溝難度越大，在巖石或常有巖石露出的地區進行開溝的難度特別大[11-12]。軟件模擬結果顯示，挖溝后管道可免受部分水動力載荷的影響，管道穩性得到增強。

進行挖溝措施后，頂部圓弧的一端與12 m水深的海床相切，另一端與坡度為25°的海床相切，整個頂部圓弧曲率約為0.001 7 m-1，保證管道在斜坡頂端的平穩過渡。挖溝效果如圖5所示。

4 斜坡底端優化措施

針對斜坡底端，通過懸鏈線理論計算出斜坡底部管線懸鏈線長度和曲率，據此設計海底管道在斜坡底端的布置形式，并根據懸鏈線距海底最大垂直距離選擇機械支撐或填沙袋的工程措施[13-14]。

自然懸鏈線的形態可以表示為

(4)

式中：x為從觸地點到計算點的水平距離；z為計算點到海底的高度；Th為海床上管子內部的水平力；ws為單位管長的水中重量。

曲率為

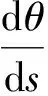
(5)

式中：θ為計算點與x軸的水平夾角；s為弧長。

管道懸跨部分的弧長可以通過下式計算得到：

(6)

根據懸鏈線理論進行計算，得到斜坡底端懸鏈線懸跨長度約400m，曲率約為0.005m-1，弧長距海底最大垂直距離8m。根據懸鏈線理論優化后的管線形態如圖6所示。

圖5 挖溝效果圖Fig.5 Trenching design sketch

圖6 斜坡末端懸鏈線示意圖Fig.6 Catenary optimization design for the end of the slope

從懸跨管道運行的可靠性角度分析，管道懸跨段高度超過3m時應使用機械支撐法保證強度要求[15]。在本文中，由于最大垂直距離為8m，大于3m，所以在整個管線懸鏈線與海床之間建議使用機械支撐加以支持固定，防止管線出現變形等現象。

5 工程優化后強度分析

對斜坡頂端和斜坡底端進行工程措施優化后，在運營工況和水壓測試兩種工況下再次對大坡度海底管道進行強度模擬計算。在每個工況下得到不同工程措施組合(頂部托管架+底部懸鏈線、頂部挖溝+底部懸鏈線)的應力結果，進行校核。

5.1運營工況分析

運營工況下，計算結果如圖7和表6所示。

圖7 運營工況最大等效應力曲線Fig.7 Maximum equivalent stress under operating condition

應力頂部托管架+底部懸鏈線優化頂部挖溝+底部懸鏈線優化取值出現位置/m取值出現位置/m最大等效應力338．5MPa0324．9MPa0最大彎曲應力59．48MPa203049．93MPa1840有效張力43997kN042470kN0

由圖7可見，最大等效應力最大值小于358.54 MPa，符合規范要求。由表6可知，最大等效應力最大值和有效張力最大值出現在管道的最頂端。管道頂端承受著管線自身的重量，導致管線有效張力在管線頂端達到最大，并使得最大等效應力在管線頂端數值最大。

5.2 水壓測試工況分析

水壓測試時，對管內進行沖水加壓。模擬計算結果如圖8和表7所示。

圖8 水壓測試最大等效應力曲線圖Fig.8 Maximum equivalent stress under water pressure condition

應力頂部托管架+底部懸鏈線優化頂部挖溝+底部懸鏈線優化取值出現位置/m取值出現位置/m最大等效應力344．5MPa0331．4MPa0最大彎曲應力59．48MPa203049．93MPa1840有效張力44249kN043326kN0

比較表6和表7所示結果，在水壓測試工況下，最大等效應力最大值有所增加，最大彎曲應力的數值和位置沒有變化，有效張力最大值仍出現在管線頂端。圖8與圖7最大等效應力趨勢相同，頂端應力最大。在兩種工況下，最大等效應力最大值均小于358.54 MPa，符合規范要求。因此，文中所選擇的工程措施可以實施。

實際工程中，應根據水深、海底海況、海床的承受能力以及經濟等因素選擇最合適的工程處理措施。本文中，由于12 m水深處托管架鋪設難度較大，而且托管架的尺寸較大不利于工程鋪設，故建議選擇挖溝措施進行優化。

6 結 語

大坡度海底管道鋪設地形復雜。進行在位強度分析，包括對鋼管壁厚的校核和載荷組合控制分析，能夠通過校核管道強度來調整管道參數的設計，為選擇最安全、經濟的工程施工方案提供參考。本文模擬南海海底的大坡度管道，對其進行強度分析。強度分析中，確定了應力不符合規范的管線位置并提出了相應的工程優化措施。優化設計后，在兩種工況下大坡度海底管線強度均符合規范要求。通過研究分析得出如下結論：

(1) 大坡度海底管線在斜坡頂端和底端位置所受的應力變化較大，容易發生強度破壞。

(2) 在斜坡頂端可選用兩種工程措施進行優化，即建立托管架和挖溝。這兩種工程措施都可以有效減小斜坡頂端的曲率進而減小管道所受應力。具體方法的選擇應根據海底海況等因素而定。

(3) 斜坡末端使用自然懸鏈線法進行優化設計。通過懸鏈線理論計算出斜坡底部管線懸鏈線長度、曲率等，采取相應措施，可以有效減小管線底端所受應力。

[1] 晏清. 國際海洋可再生能源發展及其對我國的啟示[J]. 生態經濟,2012(8):33.

[2] 余志兵, 陳海龍. 海底管道在位強度分析[J]. 中國造船,2007,48(增刊):591.

[3] Choi H S. Free spanning analysis of offshore pipelines[J]. Ocean Engineering,2001,28(10):1325.

[4] Feng H, Duan M L, Wang D G, et al. Research development of deepwater pipelaying technology and facilities[J]. Advanced Materials Research,2012,452-453:289.

[5] 繆國平. 撓性部件力學導論[M]. 上海：上海交通大學出版社，1995.

[6] Yuan Z,Huang Z.Morison coefficients for a circular cylinder oscillating with dual frequency in still water:an analysis using independent-flow form of Morison’s equation[J].J Ocean Engineering and Marine Energy,2015,1(4):435.

[7] 康莊, 張立, 劉禹維, 等. 頂部張緊式立管強度設計分析[J]. 船舶工程,2015,37(3):74.

[8] 王林. 深海托管架概念設計要素研究[D]. 大連: 大連理工大學,2008:15-27.

[9] Brown R J, Palmer A. Developing innovative deep water pipeline construction techniques with physical models[J]. Journal of Offshore Mechanics and Arctic Engineering,2007,129(1):56.

[10] 張向鋒. 深水S型鋪設托管架基本設計關鍵力學問題研究[D]. 大連: 大連理工大學,2014:41-46.

[11] 李成鋼, 張敬安, 鄭輝, 等. 海底管道懸跨維護技術研究[J]. 中國石油和化工標準與質量,2013(7):112.

[12] 秦衛華. 海底管道挖溝技術的改進[J]. 江蘇船舶,2010(1):18.

[13] Kashani M, Young R. Installation load consideration in ultra-deepwater pipeline sizing[J]. Journal of Transportation Engineering,2005,131(8):632.

[14] 白興蘭, 段夢蘭, 李強. 基于整體分析的鋼懸鏈線立管觸地點動力響應分析[J]. 工程力學,2014(12):249.

[15] Chakrabarti S. Handbook of Offshore Engineering, Volume2[M]. Oxford, UK: Elsevier,2005:891-933.

StrengthAnalysisofSubmarinePipelineonLargeSlope

WANG Bo-ya1, KANG Zhuang1, SONG Ru-xin1, CAO Xian-fan2, LIU Zhen-wen2

(1.DeepwaterEngineeringResearchCenter,CollegeofShipbuildingEngineering,HarbinEngineeringUniversity,Harbin,Heilongjiang150001,China2.CNPCResearchInstituteofEngineeringTechnology,KeyLaboratoryofOffshoreEngineeringofCNPC,Tianjin300451,China)

Large slope pipeline is an essential type of submarine pipeline in the development of oil and gas. Based on the landform of the South China Sea, the structural strength of the large slope pipeline is studied and engineering optimization methods are proposed. By analyzing the governing equations of pipeline structure, the key parameters influencing the force analysis are obtained. The structural strength of the pipeline is calculated by the nonlinear time domain software. It turns out that pipelines at the top and bottom of the slope are easily damaged. For engineering optimization, establishing a stinger and trenching are suggested for the top pipeline, and catenary theory optimization design is adopted for the bottom pipeline. Through further analysis, it is concluded that the strength of large slope pipeline after optimization design can meet the standard.

submarine pipeline; large slope; strength calculation; engineering optimization method

TE973.92

A

2095-7297(2015)04-0264-06

2015-07-12

王博雅(1991—)，碩士研究生，主要從事海底管道和渦激振動方面的研究。