坐標本征態的Fock表象表示*

林 蓉

(菏澤學院物理與電子工程系，山東菏澤274015)

引言

Dirac證明了薛定諤的波動力學與海森堡的矩陣力學的統一性，并且創造性的引入了Dirac符號，Dirac符號是量子力學理論最普遍的表述［1］．許多教材［2～4］闡述了波函數在不同表象中，如動量表象、角動量表象等的表示形式，由此可以得出描述微觀粒子的態可以在任何表象下表示出，即態矢不依賴于任何表象．本文利用線性諧振子本征態│n〉的完備性導出了坐標本征態│x〉在Fock表象下［5］的表達式．在Fock表象中計算簡潔，而且用途越來越廣．

1 薛定諤方程

在量子力學中，微觀粒子的狀態大多用波函數描寫，但決定粒子狀態變化的是薛定諤方程，它描寫勢場U→)中粒子狀態隨時間的變化．

薛定諤方程為:

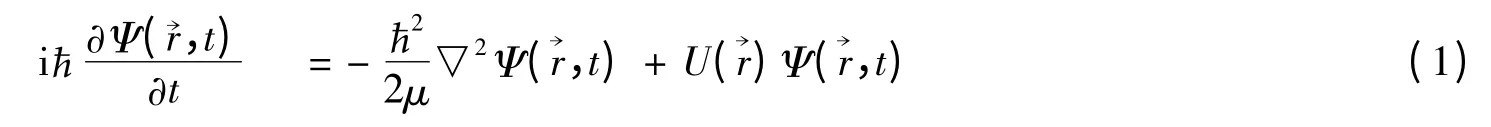
如果U(→r)不含時間則(1)式的解可用分離變量法進行簡化，考慮一特解

將(2)式代入(1)式并對方程進行計算可得到定態薛定諤方程:

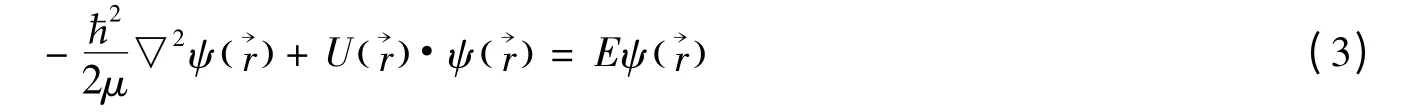
所謂定態就是指能量具有確定值的狀態．

2 狄喇克符號

在幾何學或經典力學中，常用矢量形式討論問題而不指明坐標系，同樣，在量子力學中，描寫態和力學量也可以不用具體表象，這種描寫方式是狄喇克最先引用的，因此這樣的一套符號稱為狄喇克符號．

微觀體系的狀態可以用一種矢量來表示，它的符號是│〉，稱為刃矢，簡稱刃，也稱為右矢，某一確定的刃矢A可用符號│A〉表示．微觀體系的狀態也可以用另一種矢量來表示，這種矢量的符號是〈│，稱為刁矢，簡稱刁，也稱為左矢，某一確定的刁矢B可用符號〈B│表示．

刃和刁是兩種不同的矢量，二者不能相加，它們在同一種表象中的相應分量互為共軛復數．│A〉在Q表象中的分量為{a1，a2，…an…}，那么〈A│在Q表象的分量為}．和│A〉〈B│在同一表象中相應分量的乘積之和稱為│A〉和〈B│的標積，用符號〈B|A〉表示．用表示〈B│在Q表象中的分量，那么顯然〈B│A〉和〈A│B〉互為共軛復數，即:

設│A〉為表示某一狀態的刃，這個態在x表象中以波函數Ψ(x，t)描寫，Ψ(x，t)就是刃│A〉在x表象中的分量，由于基刃│x〉組成完全系，所以│A〉可以按│x'〉展開:

以〈x│左乘上式兩邊，并且利用坐標x的本征態正交歸一條件:

可得:

由(4)式和(7)式可得:

3 Fock表象的引入

量子力學中態和力學量的具體表示方式稱為表象．常見的表象有坐標表象、動量表象、能量表象、角動量表象和Fock表象．

3．1 線性諧振子

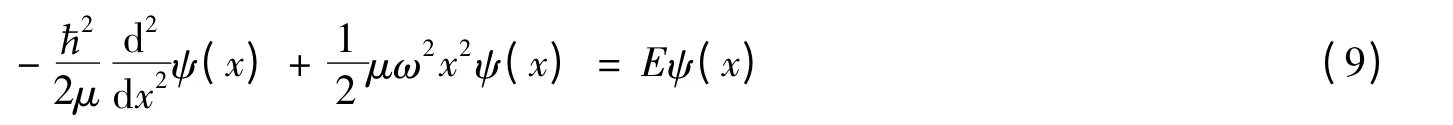
引入沒有量綱的變量ξ代替x，它們的關系是

其中Hn(αx)為厄密多項式，Nn是歸一化常數，且

Hn(ξ)=Hn(αx)滿足遞推關系［6］:

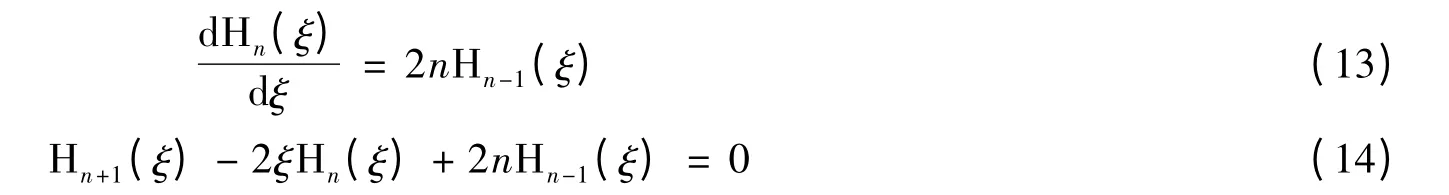
3．2 本征矢│n〉的封閉性

Q表象的正交歸一基矢全體集合為{│n〉，n=1，2，3…}，是完備的，任意態矢│ψ〉可以通過│n〉表示為因為│ψ〉是任意的，故

(15)式所表示的性質稱為本征矢│n〉的封閉性，也稱為完備性．通常將這組正交、歸一、完備基{│n〉}所張的空間稱為Fock空間．在Fock空間中，計算簡潔，富于粒子圖像，后繼量子力學中經常使用，且用途越來越廣．

3．3 Fock表象

引入新算符

利用(10)式可將(16)、(17)式改寫為:

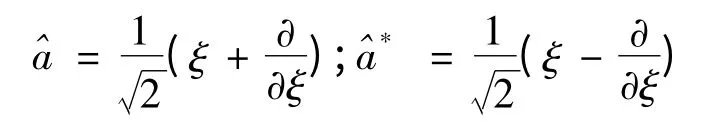
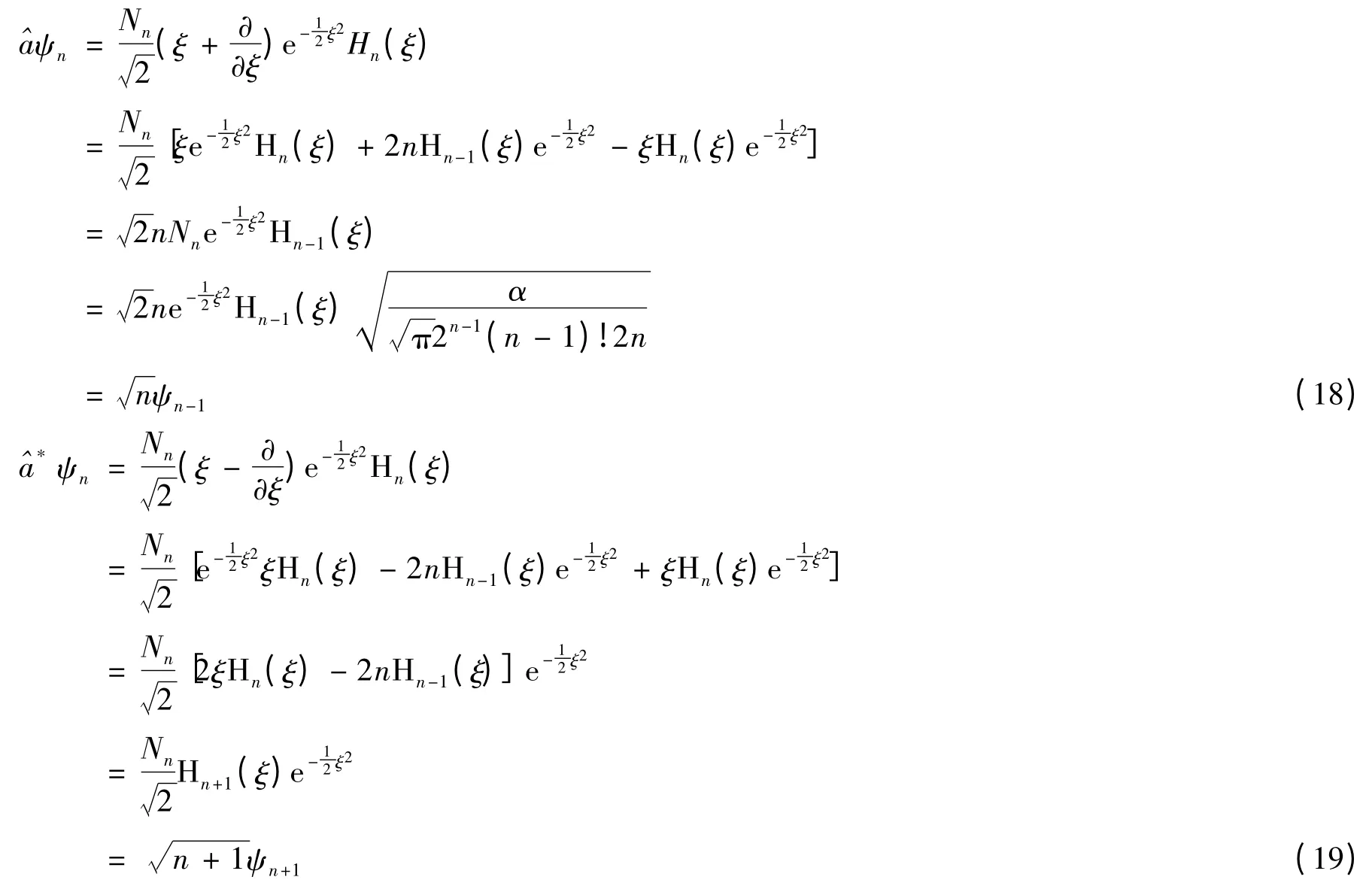
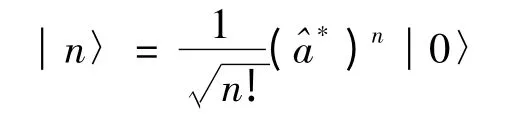
由(16)、(17)兩式可得:

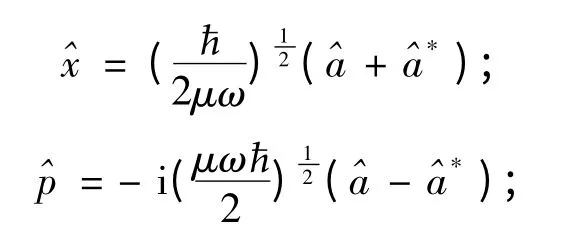
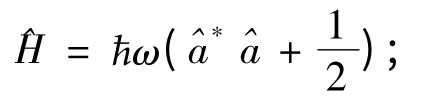
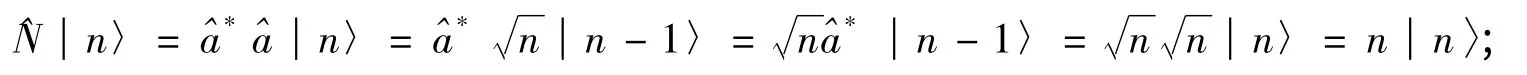
以│n〉為基矢的表象稱為Fock表象，也稱占有數表象．

4 坐標本征態的Fock表象表示

利用本征矢│n〉的封閉性:

和

以及

可得:

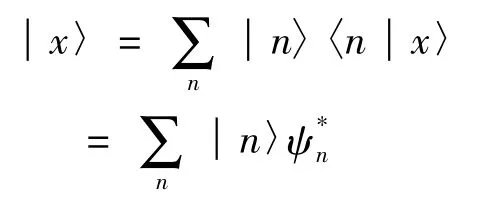
由于Ψn是實函數，所以=Ψn;

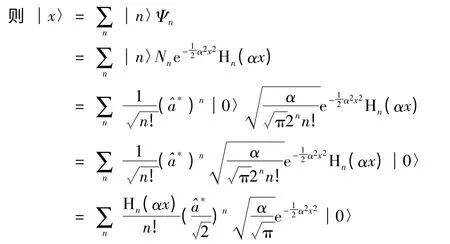
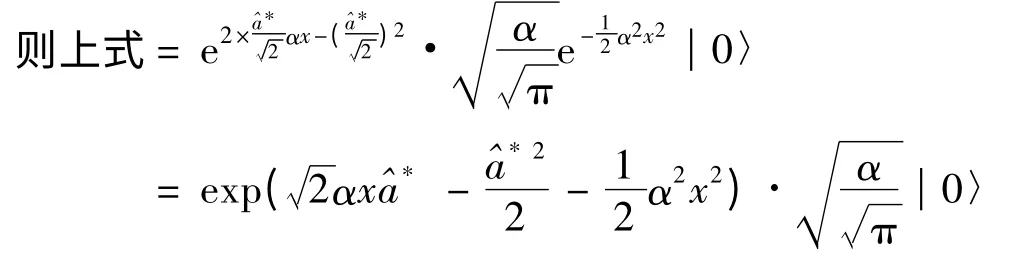
坐標本征態的Fock表象表示為:

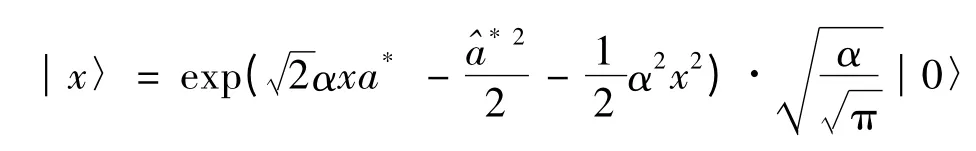
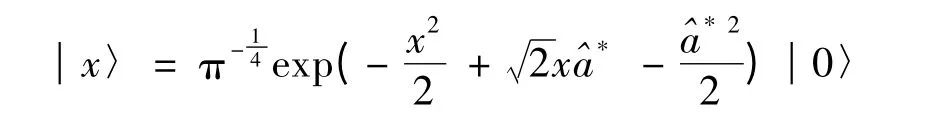
綜上所述，利用線性諧振子本征態的完備性和厄米多項式的母函數得出了坐標本征態在Fock表象中的具體表達式，方法簡潔，易于接受，并且此表達式在量子力學研究的各個領域有著重要的應用．

［1］Dirac PA M．The principles of Quantum Mechanics［M］．Oxford:Clarendon Press，1930．

［2］曾謹言．量子力學(卷Ⅰ)［M］，第四版，北京:科學出版社，2007:128－137．

［3］周世勛．量子力學教程［M］，北京:高等教育出版社，1979，2:103－111．

［4］陳鄂生．量子力學基礎教程［M］，第三版，濟南:山東大學出版社，2006，1:139－152．

［5］袁洪春，王帥，范洪義．從二維正態分布密度函數的角度研究量子力學基本表象［J］．大學物理，2011，30(12):1－3．

［6］梁昆淼．數學物理方法［M］，第三版(修訂本)，北京:高等教育出版社，1998:270－292．