關于雙圈圖的Harary指數＊

邢抱花

（安慶師范學院 數學與計算科學學院，安徽 安慶246133）

1 預備知識

連通圖G的Harary指數是一個很重要的拓撲參數，是在1993年由Plavˉsic′［1］等和Ivanciuc［2］等在刻劃分子結構圖時各自獨立提出，且為了紀念Frank．Harary七十大壽而命名的．該拓撲指數被提出之后，許多學者對它進行了大量地研究，有關它的文章被陸續發表，部分結論可參見文獻［4～8］，其中文獻［6］給出了n階單圈圖和n階雙圈圖的Harary指數的上界以及相應的極圖．本文主要研究雙圈圖去掉一條割邊或添加一條邊后其Harary指數的上界問題，并刻畫了達到上界的極值圖．

文中所涉及的圖都是有限簡單連通無向圖，雙圈圖是具有n個點和n＋1條邊的連通圖．設圖G是一個簡單連通圖，V（G），E（G）分別是它的頂點集和邊集，｜V（G）｜表示圖G的階，即頂點個數．圖G的Harar y指數定義為圖G中所有點對的距離的倒數之和，即

其中dG（u，v）是圖G中頂點u，v之間的距離，即連接頂點u，v的最短路長度．在n階星圖Sn的兩個懸掛點間添加一條邊e后得到的新圖，記為Sn＋e．設e∈E（G），若圖G－e的連通分支數大于圖G連通分支數，則稱e為G的一條割邊．?v∈V（G），v的距離是指圖G中其余頂點到頂點v的距離之和，記為DG（v）．文中沒有被定義的其他術語和符號，讀者可參見文獻［3］．

2 引理與主要結論

圖1 連通圖（n，3，3）與（n，3，3）

引理1［4］設G1，G2是連通圖G的兩個連通分支，V（G1）∩V（G2）＝｛v｝，令G＝G1v G2，則

引理2［5］設G是一個連通圖，Tn和Sn分別是階為n的一棵樹和星圖，V（H1）∩V（Tl）＝｛｝v，則

等號成立當且僅當Tn為Sn，其中在Gv Sn中v與星圖Sn的中心粘合（等同）．

引理3［6］設μ1（n）表示n階單圈圖的全體，G∈μ1（n），則等號成立當且僅當G為Sn＋e．

引理4［6］設μ2（n）表示n階雙圈圖的全體，G∈μ2（n），則等號成立當且僅當G為（n，3，3）或G為（n，3，3）．（n，3，3）（n，3，3）見圖1）

證明：設雙圈圖G＝G1v G2，其中V（G1）∩V（G2）＝｛v｝，且G1，G2分別是s，t階單圈圖，s＋t＝n＋1，則由引理1和引理3，得：

等號成立當且僅當G1為s階星圖，G2為t階星圖，且v是G1與G2的中心，即等號成立當且僅當G＝（n，3，3）．經計算故結論成立．

定理1 設G∈μ2（n），G＊表示G－e，其中e為割邊，則

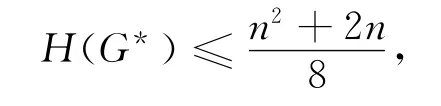
等式成立當且僅當G＊是由兩個連通分支S n2＋e和S n2＋e所構成的圖或G＊是由兩個連通分支和所構成的圖或G＊是由兩個連通分支和所構成的圖．

證明：?G∈μ2（n），圖G＊＝G－e的兩個連通分支的情況可能是：1）一個雙圈圖G1和一棵樹T1；2）兩個單圈圖G2，G3．

對于情況（1），設V（T1）＝x，V（G1）＝n－x，則由引理2和4得：

定理2 設G∈μ2（n），G＊＊表示在圖G中添加一條邊e后得到的新圖，e?E（G），則等號成立當且僅當G＊＊是星圖Sn添加兩條邊后得到的圖．

證明：由題意知，圖G＊＊是n階三圈圖，可以把它看成是一個n1階單圈圖G1與一個n2階雙圈圖G2的粘圖，即G＊＊＝G1v G2，V（G1）∩V（G2）＝｛v｝，且n1＋n2＝n＋1．

由引理3和引理4得，

等號成立當且僅當G1為Sn1＋e；G2為（n2，3，3）或G2為G＊2（n2，3，3）．

等號成立當且僅當在圖G1中，v是圖G1＝Sn1＋e中度最大的頂點，在圖G2中，v是圖G2＝（n2，3，3）中度最大的頂點或v是圖G2＝（n2，3，3）中度最大的頂點．故

等號成立當且僅當G＊＊＝（Sn1＋e）v（n2，3，3））或G＊＊＝（Sn1＋e）v（n2，3，3）），且此時頂點v是圖G1＝Sn1＋e中度最大的頂點，同時，頂點v又是圖G2＝（n2，3，3）中度最大的頂點或圖G2＝（n2，3，3）中度最大的頂點，故三圈圖G＊＊可看成星圖Sn添加兩條邊后得到的圖．

［1］Plavi D，Nikoli S，Trinajstin，etal．On t he Harar y index f or the characterization of chemical graphs［J］．Math Chem，1993，12：235－250．

［2］Ivanciuc O，Balaban S T，Balaban T A．Reciprocal diatance matrix，related local vertex invariants and topological indices［J］．Math Chem，1993，12：309－318．

［3］Bondy A，Mmurty U S R．Graph Theory with Application［M］．New York：Mac millan Press，1976．

［4］K．Xu，N．Trinajstic．Hyper－Wiener and Harary indices of graphs with cut edges［J］．Util．Math．，2011，84：153－163．

［5］K．Xu．Trees wit h the seven s mallest and eight greatest Harar y indices［J］．Discrete Applied Mathematics，2012，160（3）：321－331．

［6］K．Xu，K．C．Das．Extremal Unicyclic and Bicyclic Graphs with Respect to Harary Index［J］．Bull．Malays．Math．Sci．Soc（2），2013，36（2）：373－383．

［7］李小新，査淑萍，范益政．連通圖的Harary指數上界及其極圖［J］．中國科學技術大學學報，2014，44（2）：96－100．

［8］肖金環，趙飚．固定直徑的樹的Harary指數［J］．曲阜師范大學學報（自然科學版），2014，40（3）：30－34．