不同規范中錨桿錨固長度計算公式的探討

陳富，張健，劉愛民，于淼

（1.中交天津港灣工程研究院有限公司，港口巖土工程技術交通行業重點實驗室，天津市港口巖土工程技術重點實驗室，天津 300222；2.海洋石油工程股份有限公司，天津 300461）

0 引言

隨著大規模工程建設的發展，遇到了很多邊坡支護、基坑支護、基礎抗浮錨固等工程問題，大多數情況下需要進行加固提高其穩定性。錨桿由于其受力明確、施工方便等特點，在上述工程中得到了越來越多的應用。錨桿設計中很重要的一個設計參數為錨固段長度，這直接決定了錨桿的可靠度和成本。錨固段長度過長，往往端部的錨固體不能充分發揮其黏結強度，造成了工程浪費；錨固長度過短，會造成錨桿拔出破壞，影響工程安全。因此如何確定合適的錨固長度是各巖土工程設計規范的重要公式，既要做到保證合適的可靠度，又要避免浪費。

由于巖土工程的特殊性，巖土工程設計尚處于由安全系數設計法向概率極限狀態分項系數設計法的轉換階段，而現行各規范的巖土工程設計大多是多種設計方法并用。各規范執行不同的荷載規定，設計值與標準值（或荷載效應基本組合與標準組合）混用，不同規范按不同的安全度標準建立評價體系，很容易造成誤解和混淆[1]。

本文從現階段巖土工程設計方法的分析入手，重點介紹4本規范關于錨桿錨固長度的計算公式及相關參數取值，并通過算例來驗算4本規范錨固長度的計算差別。

1 巖土工程設計方法

首先需要明確巖土工程設計中的兩種極限狀態，一種是承載能力極限狀態，另一種是正常使用極限狀態。

承載能力極限狀態設計時，不同的安全度控制的設計方法分為定值法和概率法兩種。定值法包括單一安全系數法（又稱總安全系數法）、容許應力法和多系數法。概率法包括分項系數法和全概率法[1]。

正常使用極限狀態設計時，由于問題的復雜性，以變形、裂縫寬度為控制內涵的正常使用極限狀態計算，巖土工程如同上部結構一樣從未實現基于可靠性分析的概率極限分析狀態設計[2]。一般可以歸為容許應力（變形）法。

采用容許應力法的表達式描述正常使用極限狀態的荷載作用效應與抗力效應的關系，荷載作用效應采用標準組合，抗力效應以容許值（包括試驗曲線的某種特征點或理論公式的計算結果）表示，其安全度是隱含的，并不出現在表達式中，也就是說，在容許應力法計算中不出現安全系數或分項系數[1]。盡管說容許應力法驗算的是正常使用極限狀態，但其安全度是隱含在抗力效應容許值的取值過程中（一般取抗力效應的比例界限值或極限值除以2），實質上也可以理解為承載能力極限狀態的驗算，這點在港口工程地基承載力驗算中可以看出。

采用總安全系數設計法的表達式描述的是承載能力極限狀態的作用與抗力的平衡關系。其中，抗力效應是極限值，包括試驗曲線上的極限臨界值或根據極限理論計算的結果，荷載作用效應是標準組合[1]。總安全系數設計法的表達式見下式。

式中：K為安全系數；R為抗力函數；S為荷載作用函數。

總安全系數法在穩定性驗算中應用最廣，取得了豐富的經驗參數。

采用分項系數設計法的表達式描述承載能力極限狀態下設計驗算點的抗力效應的設計值與荷載作用效應的設計值的平衡關系。其中，抗力效應的設計值與荷載作用效應的設計值都考慮了相應的分項系數。

式中：γ0為重要性系數；Sd為荷載效應設計值；Rd為抗力設計值。

由于技術發展的側重面不同及巖土工程的特點，上部結構和巖土工程地基基礎的設計方法處于不同的發展階段。上部結構比較早的開始了向概率極限狀態設計的過渡，而巖土工程地基基礎則仍處于總安全系數設計階段，甚至有些部分尚停留在容許應力設計階段[1]。

地基承載力驗算屬于容許應力設計法，舉例來說，在地基承載力或樁基承載力的計算中，承載力特征值一般通過現場載荷試驗確定，取值時已經考慮了地基土性、受力特征等因素，不需要再考慮抗力分項系數就能夠保證足夠的可靠度。

穩定性驗算屬于總安全系數設計法，該方法經過了大量的實踐檢驗，取得了不同工況下保持穩定的相應經驗參數，能夠滿足可靠度的要求。

鑒于地基土性的不確定性對巖土工程可靠性影響目前仍處于研究探索階段，即使在巖土工程中采用承載力概率極限狀態設計模式也尚屬不完全的可靠性分析設計[2]。因此，JGJ 94—2008《建筑樁基技術規范》也從94版規范的樁基承載能力概率極限狀態分項系數的設計法改為綜合安全系數（總安全系數）設計法。相應的荷載效應的基本組合也改為荷載效應標準組合。

2 4本規范錨固長度計算公式分析

錨固長度的計算本質上是承載能力極限狀態設計，計算得到的錨固長度需要保證足夠的可靠度。但不同規范采用的荷載標準和抗力的標準不一致，有些公式荷載采用了標準組合，有的規范采用基本組合。抗力有的采用極限承載力標準值，有的采用承載力特征值。舉例來說，GB 50007—2011《建筑地基基礎設計規范》第3.0.5條規定[3]，計算擋土墻、地基或滑坡穩定以及基礎抗浮穩定時，作用效應應按承載能力極限狀態下作用的基本組合，但其分項系數取為1.0；這就與標準組合在數值上基本相同，當可變荷載控制的基本組合更是和標準組合完全一致。

以下匯總JGJ 120—2012《建筑基坑支護技術規程》、GB 50330—2002《建筑邊坡工程技術規范》、CECS 22：2005《巖土錨桿（索）技術規程》、GB 50007—2011《建筑地基基礎設計規范》4本規范中關于錨固長度計算公式，并進行相關解釋說明。錨固體與地層間的黏結強度標準值與特征值的大小關系，大多數情況下黏結強度標準值為特征值的2倍，為了對不同規范的計算結果比較分析的方便，本文直接取2倍。

2.1《建筑基坑支護技術規程》相應公式

該規范中第4.7.2條規定，錨桿的極限抗拔承載力應符合下列要求[4]：

式中：Kt為錨桿抗拔安全系數，安全等級為一級、二級、三級的支護結構，Kt分別不應小于1.8、1.6、1.4；Nk為錨桿軸向拉力標準值，kN；Rk為錨桿極限抗拔承載力標準值，kN。

該公式是很典型的總安全系數法，抗力項和荷載項都采用標準值。

2.2《建筑邊坡工程技術規范》相應公式

該規范第7.2.3條規定，錨桿錨固體與土層的錨固長度應滿足下式要求[5]：

式中：la為錨固體長度，m；D為錨固體直徑，m；frb為地層與錨固體黏結強度特征值，kPa；Nak為錨桿軸向拉力標準值，kN；ξ1為錨固體與土層黏結工作條件系數，對永久性錨桿取1.00，對臨時性錨桿取1.33。

式（4）計算公式中，抗力項采用錨桿抗拔承載力特征值，相當于隱含安全系數2，綜合考慮黏結工作條件后，對于永久性錨桿安全系數約為2.0，對于臨時性錨桿安全系數約為1.5，總體上與《建筑基坑支護技術規程》安全系數（取值1.4～1.8）相近。

2.3《巖土錨桿（索）技術規程》相應公式

該規范第7.5.1條規定，錨桿錨固長度可按下式估算[6]：

式中：K為錨桿錨固體的抗拔安全系數；Nt為錨桿或單元錨桿的軸向拉力設計值，kN；La為錨桿錨固體長度，m；D為錨桿錨固段的鉆孔直徑，m；fmg為錨固段注漿體與地層間的黏結強度標準值，kPa；ψ為錨固長度對黏結強度的影響系數。

該規范采用了總安全系數設計法，抗拔安全系數對于臨時錨桿取1.4～1.8，永久錨桿取2.0～2.2。抗力項取錨桿極限抗拔承載力標準值，荷載效應采用了設計值，但規范中并沒有指出荷載效應軸向拉力設計值的計算方法，只是在條文說明中指出拉力設計值采用工作荷載。作者認為該規范中的拉力設計值實際上是荷載標準值，即荷載分項系數取1.0，這樣抗拔安全系數的取值與上述兩本規范的取值相近。

2.4《建筑地基基礎設計規范》相應公式

該規范第9.6.6條針對錨桿設計規定：土層錨桿錨固段長度應按基本試驗確定，初步設計時也可按下式估算[3]，

式中：D為錨固體直徑；K為安全系數，可取1.6；qs為土體與錨固體間黏結強度特征值，kPa，由當地錨桿抗拔試驗結果統計分析算得；Nt為相應于作用的標準組合時，錨桿所承受的拉力值，kN。

式（6）計算中，在考慮了總安全系數K=1.6的同時，抗力項取值為錨桿抗拔承載力特征值，這相當于實際安全系數大約為1.6×2.0=3.2，過分地提高了安全系數，與上述3本規范存在比較大的差異，造成了浪費。

在抗浮穩定驗算不滿足時也會設置錨桿提供向下的力，其第5.4.3條規定，對于簡單的浮力作用情況，基礎抗浮穩定性應符合下式要求：

式中：Gk為建筑物自重及壓重之和，kN；Nw，k為浮力作用值，kN；Kw為抗浮穩定安全系數，一般情況下可取1.05。

如果設置錨桿，則需要在分子Gk上加上錨桿抗拔力特征值Fs，k，然后再計算相應的抗浮穩定安全系數Kw。該抗浮穩定安全系數Kw取值1.05比一般的穩定安全系數取值要小，這是因為抗浮穩定驗算中抗力項采用了錨桿抗拔承載力的特征值，與抗拔承載力極限值相比有了大約2.0的安全系數，此處再考慮1.05的安全系數可能與抗浮設計中的出現極端高水位、錨桿長期工作受力性能等因素有關。

3 算例結果比較

本文采用一個黏性土層錨桿錨固長度典型算例來分析各本規范錨固長度計算結果的差異。

3.1 算例計算參數

黏性土層錨桿錨固長度的計算參數見表1。

表1 算例計算參數Table 1 Calculation parametersofnumericalexamp le

3.2 計算結果比較

利用表1的計算參數，根據4本規范的相應公式，分別計算出永久錨桿和臨時錨桿的錨固長度。為了比較的方便，當規范中給出的抗拔安全系數為一個范圍時，取其所給上下限值的平均值作為抗拔安全系數帶入公式計算。忽略《巖土錨桿（索）技術規程》錨固長度對黏結強度的影響系數。計算結果見表2。

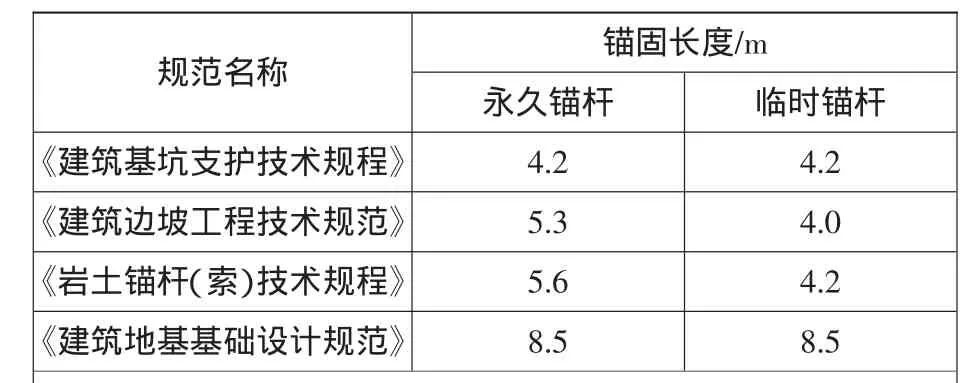
表2 算例計算結果Table 2 Calculation resultsof numericalexam ple

通過分析表2計算結果可以發現：

1）對于臨時錨桿，《建筑基坑支護技術規程》、《建筑邊坡工程技術規范》、《巖土錨桿（索）技術規程》3本規范的錨固長度計算值非常接近，說明這3本規范采用的可靠度水平也基本相同。《建筑地基基礎設計規范》的計算結果大約為前3本規范計算結果的2倍，說明其可靠度水平偏大。

2）對于永久錨桿，《建筑基坑支護技術規程》、《建筑地基基礎設計規范》采取了與臨時錨桿完全一致的計算方法；《建筑邊坡工程技術規范》、《巖土錨桿（索）技術規程》考慮了其長期工作的特點，采取了與之相適應的可靠度水平，錨固長度計算結果大約比臨時錨桿的計算結果大25%。

3）4本規范錨固長度計算公式的抗拔安全系數取值不同，計算得到的錨固長度不同，在這一簡單軸向抗拔相同的工況下，因此可靠度也不同。

4 結語

本文系統論述了巖土工程的設計方法的分類及相應的含義，并對比《建筑基坑支護技術規程》、《建筑邊坡工程技術規范》、《巖土錨桿（索）技術規程》、《建筑地基基礎設計規范》4本規范的關于錨固長度計算公式，分析了相應的巖土工程設計方法。通過一個算例驗證了不同規范的錨固長度計算值，并對計算結果進行了分析，各規范的計算結果不同，驗證了本文論述的不同規范是按不同的可靠度標準建立的評價體系。

[1]高大釗.巖土工程勘察與設計——巖土工程疑難問題答疑筆記整理之二[M].北京：人民交通出版社，2010.GAO Da-zhao.Geotechnical investigation and design：Difficult geotechnical question answering note II[M].Beijing：China Communications Press，2010.

[2]JGJ94—2008，建筑樁基技術規范[S].JGJ94—2008,Technical code forbuildingpile foundation[S].

[3]GB 50007—2011，建筑地基基礎設計規范[S].GB 50007—2011,Code for design ofbuilding foundation[S].

[4]JGJ120—2012，建筑基坑支護技術規程[S].JGJ 120—2012,Technical specification for retaining and protection ofbuilding foundation excavations[S].

[5]GB 50330—2002，建筑邊坡工程技術規范[S].GB 50330—2002,Technical code for building slope engineering[S].

[6]CECS 22：2005，巖土錨桿（索）技術規程[S].CECS22：2005,Technicalspecification forground anchors[S].