基于遙測數據的衛星在軌飛行溫度仿真算法研究

劉百麟，金 迪

(1中國空間技術研究院通信衛星事業部，北京100094;2北京空間飛行器總體設計部，北京100094)

0 引言

衛星在軌飛行溫度是評估星上設備工作性能與壽命的重要指標之一，也是保障衛星穩定運行和安全的必要條件。準確預計衛星在軌實際飛行溫度，及時調控衛星熱控狀態，將對衛星的安全和壽命起到至關重要的作用。國內、外衛星溫度預計通常采用熱分析的方法［1－3］，該方法基于衛星總體布局與傳熱學理論基礎建立熱分析模型，適用于設計、地面試驗階段具有確定邊界條件的衛星溫度場預計。航天器的熱分析主要有節點網絡法和有限元法［4－5］，由于在熱分析建模中幾何簡化、邊界條件假設、參數選擇等皆存在一定誤差，因此熱分析計算溫度與實際值必然存在偏差，為提高熱分析的準確度以便能更好地預測在軌飛行時溫度分布，通常用原型衛星的熱試驗數據對熱分析模型進行修正。李勁東［6］、程文龍等［7］全面總結與深入研究了航天器熱分析模型修正方法，指出模型修正數學處理復雜，準確度受試驗工況、試驗模擬誤差、分析者的經驗判斷等因素直接影響。另外，隨著衛星在軌實際飛行時間推移，出現如下不確定性:1)星表熱控涂層(OSR、多層及熱控漆等)熱物性性能出現退化，目前國內、外關于熱控涂層性能退化研究［8－10］局限于地面模擬試驗或飛行試驗探索性研究，其在軌真實退化規律仍不可預測;2)星上設備熱耗散隨工作效率下降而增大，其變化量級不確定;3)星上設備熱容未知;4)衛星運行目標軌道控制存在偏差。上述關乎衛星動態熱特性的在軌不確定性，再加上熱分析模型自身誤差，應用熱分析模型預示衛星在軌飛行溫度并不合適，其計算誤差是不可預估的。

近年來，針對衛星在軌飛行溫度預示方法展開相關研究，張旭東、李運澤等通過分析納衛星熱系統動態特性模型，提出基于BP神經網絡建立納衛星在軌飛行溫度預測數值計算方法［11］，該方法適用微型衛星(＜10 kg)，預測誤差受神經網絡訓練程度制約，需多次預測迭代和主觀干預合理取舍結果，自主性差。魏傳鋒等對太陽同步軌道衛星的平均溫度和外熱流簡化處理近似周期函數，采用相鄰兩個周期的在軌飛行溫度值預測下一個周期的溫度［12］，方法限定太陽同步軌道衛星使用，且僅能預測相鄰下一個周期的溫度。何治等設計一種用于衛星在軌溫度仿真的基于偏微分方程數值求解的衛星熱控分系統飛行模擬器模型［13］，模型能保證較高的仿真精度、速度，但模型構建過分依賴熱設計細節，參數變量多，系統組成龐大，運行流程復雜，與衛星其它系統存在數據交互接口，通用性差，對計算硬件配置要求很高。John等人提出應用在軌遙測數據修正熱分析模型方法，對比星上測溫點的預示溫度和實際遙測溫度進行溫度修正，通過持續更新熱模型來保證精度(偏差≤10℃)［14］，此方法預示精度低且適宜跟蹤單個部件的溫度監測。

本文提出一種基于遙測數據的衛星在軌溫度仿真算法，利用有限的衛星熱控邊界遙測溫度數據準確刻畫整星在軌飛行溫度。與現有的在軌溫度仿真方法相比，本文方法的先進性主要在于:1)方法通用性強，普適性高，不受軌道和衛星型譜限制;2)方法高保真，仿真計算精度高，可消除衛星在軌動態熱特性不確定性影響;3)模型參數少、維度低，有效地避免剛性問題及實現計算解耦;4)算法簡便，運算高效、快捷;5)運算系統配置要求極低。

1 仿真計算原理

衛星在軌運行空間環境近似真空，故只存在傳導與輻射換熱。分析衛星艙內傳熱關系可知，星內存在三種換熱途徑:設備與安裝艙板的接觸導熱、設備與艙板的輻射換熱、設備之間的輻射換熱。衛星艙內設備的熱網絡模型如圖1所示，以設備為控制體，其能量守恒集總參數數學模型如式(1)。

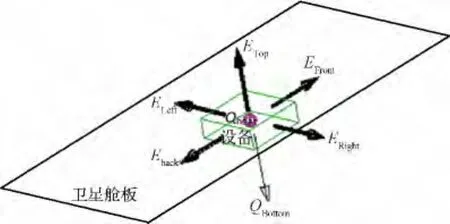
圖1 設備熱網絡模型圖Fig.1 Thermal network model of unit heat dissipation

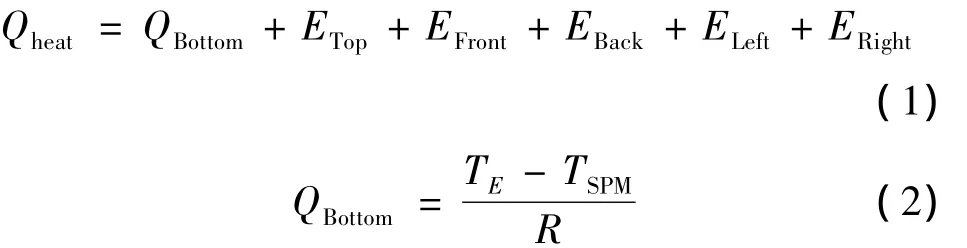
式中:Qheat為設備發熱量/W;QBottom為設備安裝底面與安裝艙板間的接觸導熱量/W;ETop為設備頂面板與艙板及其它設備間的輻射熱量/W;EFront為設備前面板與艙板及其它設備間的輻射熱量/W;EBack為設備后面板與艙板及其它設備間的輻射熱量/W;ELeft為設備左面板與艙板及其它設備間的輻射熱量/W;ERight為設備右面板與艙板及其它設備間的輻射熱量/W;TE為設備溫度/℃;TSPM為設備的安裝艙板溫度/℃;R為設備與其安裝艙板間的熱阻/(℃/W)。

上述三種熱交換途徑中，設備與其安裝艙板之間的接觸導熱占主導地位，是設備散熱的主要路徑，安裝艙板的溫度水平決定了設備溫度水平;由于設備表面積小且與其它換熱對象之間溫差較小，另外兩種熱輻射對設備溫度影響相對很小。此外在全壽命期內衛星艙內溫度變化幅度相對較小，因此由輻射引起的換熱量變化量亦很小，除設備安裝底面外的其它5個面板的輻射熱量可近似為常量。由式(1)、(2)，星內設備溫度的簡化熱數學模型可描述如下:

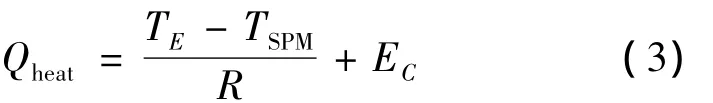
式中:EC為設備各面板輻射總熱量/W(即EC=ETop+EFront+EBack+ELeft+ERight)。

由式(3)可得到:

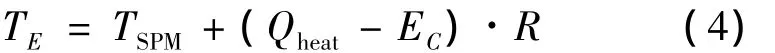
一般情況下，在設備安裝方式與工作狀態確定的前提下，熱阻(R)、設備發熱量(Qheat)兩個物理量均為恒定值，EC可近似為常值，故公式(4)中(Qheat－EC)·R可按常量處理。通過某在軌衛星全壽命周期內設備與其安裝艙板的遙測溫度(隨機選取)比較(詳見表1)可知，在11年的全壽命周期內該常量(ΔTi)變化最大偏差＜1℃(且含衛星遙測測溫系統誤差)，由此可證明上述近似的合理性。

表1 衛星設備與其安裝艙板的遙測溫度比較Table 1 Comparison of telemetry temperature between units and panels

綜上所述，衛星星內設備溫度與其安裝艙板溫度之間存在某種定量關系，在已知設備的安裝艙板溫度時，由公式(4)可直接計算設備溫度。

2 仿真方法描述

本文的衛星飛行溫度預計是基于在軌遙測數據的仿真計算方法:從衛星溫度遙測參數中選取相關參數定義為仿真模型基準溫度，根據基準溫度分布建立其控制域范圍，控制域內的設備溫度為所屬溫度域的元素;基于衛星在軌溫度遙測數據，運用數理統計挖掘元素與基準溫度之間的定量數值關系，形成衛星溫度關系數值矩陣。通過對基準溫度的遙測數據與衛星溫度關系數值矩陣之間代數運算，實現整星歷史或當前飛行溫度仿真計算;在此基礎上，對基準溫度進行外推可實現未來飛行時域衛星溫度仿真預計。衛星溫度仿真計算流程如圖2所示。

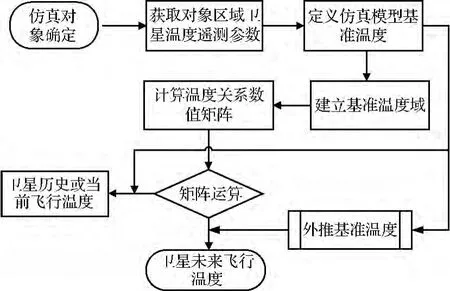
圖2 衛星在軌飛行溫度仿真計算流程圖Fig.2 Simulation flow chart of satellite temperature on orbit

1)衛星溫度遙測參數

衛星溫度遙測點一般分布在設備機殼表面和結構板內表面，其中大部分測溫點分布在設備機殼表面直接測量設備溫度，屬于相關分系統設備溫度遙測點;僅有少部分測溫點分布在設備的安裝艙板表面或結構件表面，用于衛星熱控邊界溫度測量，屬于熱控或結構分系統溫度遙測點。2)定義模型基準溫度

根據衛星總體布局與溫度遙測參數分布，選取衛星熱控邊界溫度遙測參數定義為仿真模型基準溫度，基準溫度分為兩類:一類是主體基準溫度，即衛星熱控邊界遙測溫度;另一類是個體基準溫度，即采取自主控溫或受衛星本體熱影響小的設備殼體遙測溫度。

主體基準溫度一般為星上設備集中安裝區域的艙板溫度，通常在衛星熱控(或結構)分系統溫度遙測點中選取，作為模型主體基準溫度核心。

個體基準溫度因自主控溫或受衛星本體熱影響小而具有相對獨立的變化規律，一般為星外自主控溫的設備溫度，以及星內有特殊控溫要求采取隔熱設計或自主控溫的設備溫度。

3)建立基準溫度域

主體基準溫度定義后，劃分主體基準溫度控制域范圍。根據主體基準溫度分布，以主體基準溫度測溫點位置坐標為幾何中心，以其所在的熱管網絡或艙板溫度梯度小于5℃的溫度場域為主體基準溫度控制域范圍(簡稱溫度域)，分布在溫度域內的設備(自主控溫設備除外)溫度為所屬元素。按此方法，每個主體基準溫度對應一個溫度域，溫度域內包含若干元素，域內所有元素均與域主體基準溫度之間存在某種確定的數量關系。

個體基準溫度定義后，所有個體基準溫度構成一個溫度域，即某些具有獨立變化規律的設備遙測溫度組成一個集合，其中每個個體基準溫度稱為元素。與主體基準溫度域不同的是，個體基準溫度域不存在域基準溫度，域內各元素之間也不存在任何關聯。

4)溫度關系數值矩陣計算

溫度關系數值矩陣計算只適用于主體基準溫度域。根據前文分析，主體基準溫度域是按主體基準溫度分類定義的，元素是溫度域的最小單元，用元素溫度增量來表示元素與所屬溫度域主體基準溫度之間的數量關系。元素溫度增量采用遙測數據直接求差法計算，即元素遙測值與同一時刻所屬域的主體基準溫度遙測值代數求差，其代數差值為該元素的溫度增量，算法如公式(5)。

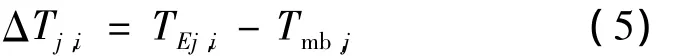
式中:ΔTj，i為溫度域 j中元素 i的溫度增量/℃;TEj，i為溫度域j中元素i的遙測溫度/℃;Tmb，j為溫度域j的主體基準溫度遙測數據/℃。

一般情況下，元素的溫度增量為樣本數據統計平均值，計算時首先截取在軌飛行時域作為取樣時間長度，在取樣時間長度內選取一定數量的計算時刻為采樣計算點，將元素與其域主體基準溫度同一采樣時刻的在軌遙測數據代入公式(5)計算出采樣計算點對應的溫度增量，各采樣計算點的溫度增量按算術平均取值，其算術平均值作為元素的溫度增量。顯而易見，延長取樣時間長度或增加取樣樣本數量，以及加密采樣計算點均可減小元素溫度增量的計算誤差，但代價是計算量大增。因此，應根據計算精度要求，選取適宜的取樣時間長度、樣本數量和采樣計算點。

綜上所述，每個主體基準溫度對應一個溫度域，主體基準溫度與其域所屬元素之間的關系可用溫度增量表征，因此，建立全部基準溫度與元素之間的溫度增量，形成一個衛星溫度關系數值矩陣，衛星溫度關系數值矩陣表如表2。

表2 衛星溫度關系數值矩陣表Table 2 Relation matrix of satellite temperature

由表2的衛星溫度關系數值矩陣列表，通過基準溫度的遙測數據與元素溫度增量之間的運算關系即可刻畫出整星溫度。此外，當星上設備與加熱器工作模式發生變化時，應采集工況變更后的衛星在軌溫度遙測數據重新計算溫度關系數值矩陣，通過持續更新衛星溫度關系數值矩陣來消除設備、加熱器工作狀態變化帶來的影響。

3 仿真方法驗證

本文衛星飛行溫度仿真計算方法將運用GEO、LEO在軌衛星飛行溫度遙測數據進行驗證，具體驗證方法是通過衛星飛行歷史數據樣本(艙板、設備溫度遙測數據)建立衛星溫度關系數值矩陣，根據擬預示時刻的衛星基準溫度遙測數據與衛星溫度關系數值矩陣之間的運算結果，獲取星上設備該時刻的預示溫度，將設備預示溫度與同時刻(擬預示時刻)的星上設備在軌實際遙測溫度比對，以此驗證和評估本文計算方法的正確性及準確度。

擬選的GEO衛星平臺艙板測溫點很少，因而選取服務艙南板、北板中心區域設備遙測溫度，以及載荷艙東板、南板、北板遙測溫度為模型主體基準溫度;蓄電池、貯箱、氣瓶、管路和推力器的遙測溫度為個體基準溫度。取樣時間長度為2009年全年，采樣時刻為每月22日0:00、6:00、12:00和18:00，共計48個采樣計算點。

擬選的LEO衛星(軌道周期:107 min)，以+X長隔板/短隔板、－X長隔板/短隔板、載荷艙的底板、隔板及頂板的遙測溫度為模型主體基準溫度;蓄電池、貯箱、管路和推力器的遙測溫度為個體基準溫度。取樣時間長度為2010年7月，采樣時刻為1日、15日和30日每天0:00、1:47、12:00 和 13:47，共計12個采樣計算點。

按上文衛星溫度仿真計算流程與算法分別計算GEO衛星、LEO衛星溫度關系數值矩陣，建立仿真計算模型進行運算求解衛星溫度。隨機抽取20個溫度遙測點(平臺與載荷艙)的仿真計算結果與在軌遙測數據比較與分析，詳見圖3～圖6。

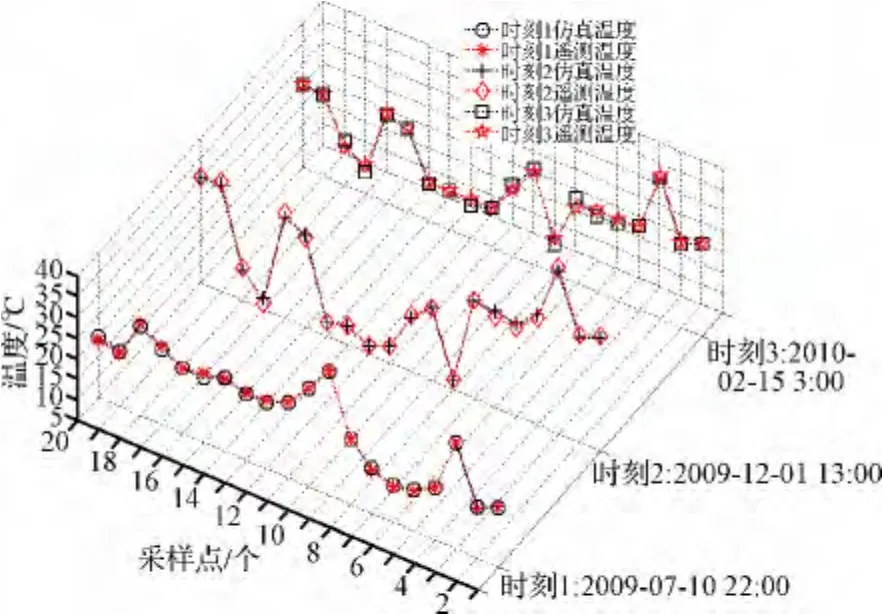
圖3 GEO衛星仿真溫度與在軌遙測溫度比較Fig.3 Comparison between simulation and telemetry temperature on GEO orbit

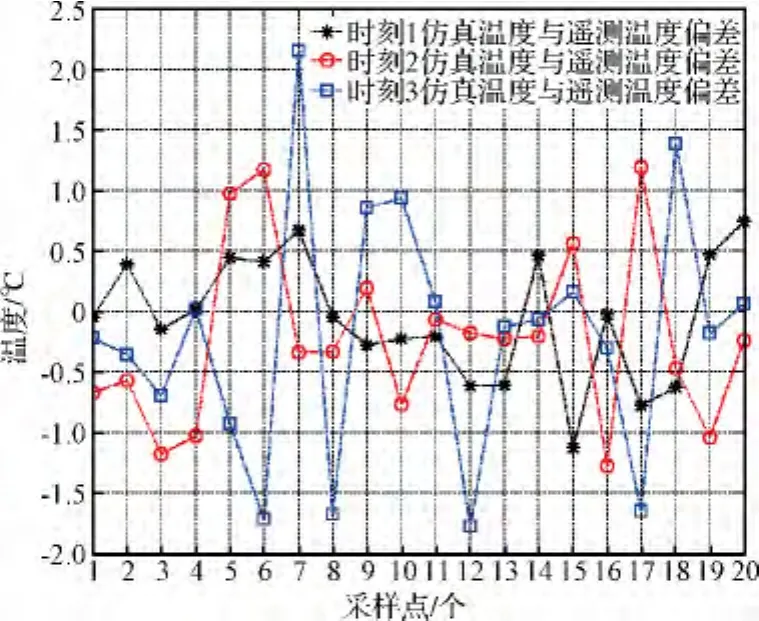
圖4 GEO衛星仿真溫度與在軌遙測溫度偏差Fig.4 Error between simulation and telemetry temperature on GEO orbit

統計分析結果表明:GEO衛星飛行溫度仿真計算偏差 ΔT ≤1℃為78.3%，1℃ ＜ ΔT ≤2℃為20%，2℃ ＜ ΔT ＜2.5℃為1.7%;LEO衛星飛行溫度仿真計算偏差 ΔT ≤1℃為95%，1℃ ＜ ΔT ＜2℃為5%。可見，本文衛星飛行溫度仿真算法誤差小于2.5℃，明顯優于國內外衛星熱分析計算誤差［15－16］。

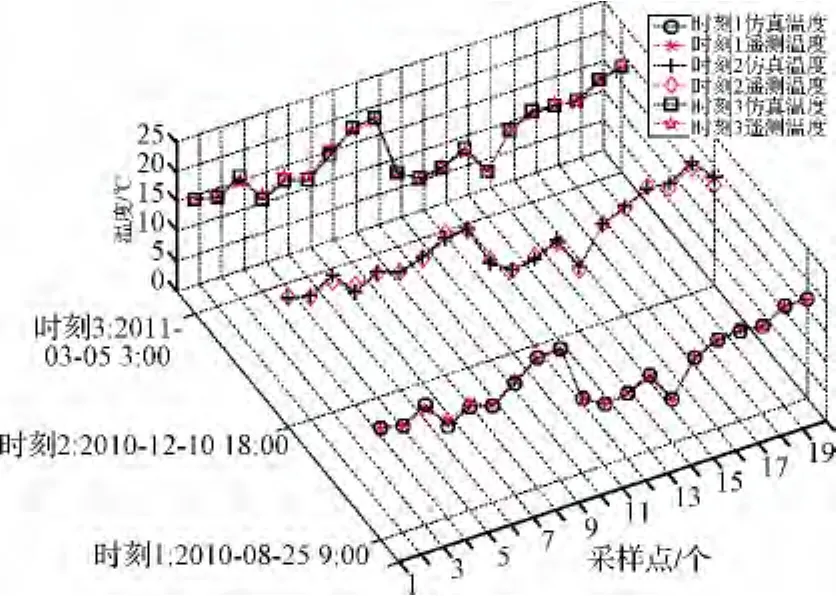
圖5 LEO衛星仿真溫度與在軌遙測溫度比較Fig.5 Comparison between simulation and telemetry temperature on LEO orbit

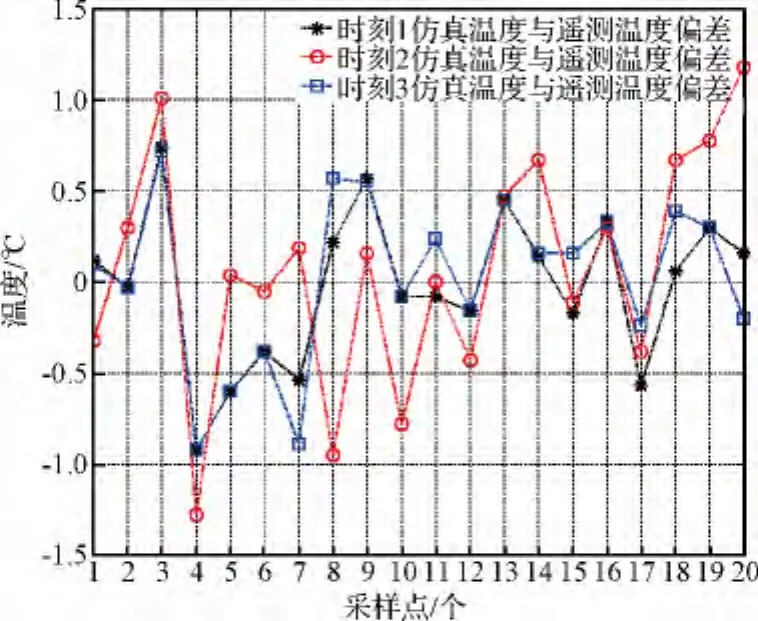
圖6 LEO衛星仿真溫度與在軌遙測溫度偏差Fig.6 Error between simulation and telemetry temperature on LEO orbit

4 結束語

本文以衛星換熱原理與衛星遙測溫度分布為理論研究基礎，提出一種基于遙測數據的衛星在軌飛行溫度仿真計算方法，通過建立設備與安裝邊界之間的溫度關系數值矩陣，利用有限的衛星熱控邊界溫度遙測數據及外推，準確地刻畫衛星在軌飛行溫度，并經過GEO、LEO在軌衛星飛行數據全面驗證，結果表明:(1)計算方法普遍適用于衛星在軌飛行溫度預計，可消除在軌階段熱控涂層退化、設備熱耗散規律模糊等不確定因素對預計精度的影響;(2)衛星熱控邊界溫度遙測參數不足時，可選區域中心的設備溫度遙測參數作為溫度域主體基準溫度;(3)結合軌道變化規律分時域建立衛星溫度關系數值矩陣，或加密采樣時間點，均能有效提高仿真計算精度，計算誤差可控制在2.5℃以內。

通過外推任意飛行時刻的衛星基準溫度與衛星溫度關系數值矩陣進行運算可預計衛星未來飛行溫度。本文給出基準溫度外推初步理論算法:Tmbj，t=為t時刻溫度域j基準溫度預計值/℃;Tmbj，0為計算起始時刻溫度域j基準溫度遙測值/℃;ΔQout為溫度域j吸收外熱流增量/W;σ為玻爾茲曼常數;εj為溫度域j外表面紅外發射率;Aj為溫度域j外表面積/m2。上述外推算法中，基準溫度變化主要取決空間外熱流［17－18］的變化規律，外熱流增量計算難點在于溫度域外表面熱控涂層太陽吸收比的退化增量，后續應結合熱控涂層太陽吸收比退化規律研究進一步完善本文外推算法。

［1］ 閔桂榮，郭舜.航天器熱控制［M］.北京:科學出版社，1998.

［2］ 屈金祥.航天器系統熱分析綜述［J］.紅外，2004，10:20－27.［Qu Jin-xiang.Review of thermal analysis for spacecraft system［J］.Infrared，2004，10:20 －27.］

［3］ Silva D F，Garcia E C.Profiles of external thermal loads in transient condition for the itasat satellite［C］.3rdCTA-DLR Workshop on Data Analysis ＆ Flight Control，SP，Brazil，September 14－16，2009.

［4］ 唐占文.高熱流密度航天器精確熱分析方法研究［D］.哈爾濱:哈爾濱工業大學，2008.［Tang Zhan-wen.The algorithm research on spacecraft thermal calculation under the high heat fluxes［D］.Harbin:Harbin Institute of Technology，2008.］

［5］ 賈震江.衛星熱分析建模方法研究［D］.南京:南京理工大學，2004.［Jia Zhen-jiang.The research on satellite thermal analysis［D］.Nanjing:Nanjing University of Science and Technology ，2004.］

［6］ 李勁東.衛星熱網絡模型修正技術進展及其改進方法研究［J］.中國空間科學技術，2004，24(3):29-37.［Li Jin-dong.Development and modification of thermal network correction techniques for satellites［J］.Chinese Space Science and Technology，2004，24(3):29 －37.］

［7］ 程文龍，劉娜，鐘奇，等.衛星穩態熱模型參數修正方法研究［J］.宇航學報，2010，31(1):270 －275.［Cheng Wen-long，Liu Na，Zhong Qi，et al.Study on parameters correction method of steady-state thermal model for spacecraft［J］.Journal of Astronautics，2010，31(1):270 －275.］

［8］ Donald A J，George C T ，David T W ，et al.Optical properties of thermal control coatings after weathering，simulated ascent heating，and simulated space radiation exposure［R］.NASA 2008 －215259.

［9］ Feng W Q，Ding Y G，Yan D K，et al.Space combined environment simulation test onαsdegradation of GEO satellite thermal control coatings［J］. Spacecraft Environment Engineering，2007，24(1):27 －31.

［10］ 馬偉，宣益民，韓玉閣，等.長壽命衛星熱控涂層性能退化及其對衛星熱特征的影響［J］.宇航學報，2010，31(2):568－572.［Ma Wei，Xuan Yi-min，Han Yu-ge，et al，Degradation performance of long-life satellite thermal coating and its influence on thermal character［J］.Journal of Astronautics，2010，31(2):568 －572.］

［11］ 張旭東，李運澤.基于BP神經網絡的納衛星軌道溫度預測［J］.北京航空航天大學學報，2008，34(12):1423 －1427.［Zhang Xu-dong，Li Yun-ze.Temperature prediction for nano satellite on orbit based on BP neu raI network［J］.Journal of Beijing University of Aeronautics and Astronautics，2008，34(12):1423 －1427.］

［12］ 魏傳鋒，李運澤，袁領雙，等.太陽同步衛星在軌運行溫度預測［J］.中國工程科學，2005，7(2):73 －75.［Wei Chuan-feng，Li Yun-ze，Yuan Ling-shuang，et al.Temperature prediction for sun synchronous satellite on orbit［J］.Engineering Science，2005，7(2):73 －75.］

［13］ 何治，許曉冬，趙啟偉.一種衛星飛行模擬器的熱控分系統模型設計［J］.航天器工程，2011，20(1):82 －87.［He Zhi，Xu Xiao-dong，Zhao Qi-wei.Design of thermal control subsystem for flying satellite simulator［J］.Spacecraft Engineering，2011，20(1):82 －87.］

［14］ John A D，Joseph F G，George B E.Thermal analysis and correlation of the mars odyssey spacecraft＇s solar array during aerobraking operations［C］. AIAA/AAS Astrodynamics Conference，Monterey，August 5 －8，2002.

［15］ Gilmore D G.Spacecraft thermal control handbook，Volume I:Fundamental Technologies［M］.El Segundo，California:The Aerospace Press，2002.

［16］ GJB 1027A－2005，運載器、上面級和航天器試驗要求［S］.

［17］ 薛豐廷，湯心溢.空間目標熱分析建模研究［J］.紅外技術，2008，30(1):35 － 38.［Xue Feng-ting，Tang Xin-yi.Study on thermal analysis of the space target［J］.Infrared Technology，2008，30(1):35 －38.］

［18］ 鐘奇，文耀普，李國強.近地熱環境參數對航天器溫度影響淺析［J］.航天器工程，2007，16(3):74 － 77.［Zhong Qi，Wen Yao-pu，Li Guo-qiang. Influences of near-earth thermal environment parameters on spacecraft temperature［J］.Spacecraft Engineering，2007，16(3):74 －77.］