滿足規范剪重比要求的高層結構基本自振周期研究＊

王福明，沈蒲生

（湖南大學 土木工程學院，湖南 長沙 410082）

由于地震影響系數在長周期段下降較快，對于基本周期大于3．5s的結構，由此計算所得的水平地震作用下的結構效應可能太小．而對于長周期結構，地震動態作用中的地面運動速度和位移可能對結構的破壞具有更大影響，出于結構安全的考慮，我國《建筑抗震設計規范》（GB 50011—2010）［1］和《高層建筑混凝土結構技術規程》（JGJ 3—2010）［2］提出了對結構總水平地震剪力系數及各樓層水平地震剪力系數（又稱為剪重比）最小值的要求，規定了不同烈度下的最小樓層地震剪力系數，當不滿足時，需改變結構布置或調整結構總剪力和各樓層的水平地震剪力使之滿足要求．《建筑抗震設計規范》和《高層建筑混凝土結構技術規程》引入樓層最小剪力系數λmin來保證長周期結構在地震作用下的安全是合適的．各國規范關于最小剪力系數也有相應的規定．

1 中國規范與美國等國規范中最小地震剪力系數的有關規定

中國與美國等國的規范都對最小地震剪力系數進行了相關的規定．

1．1 美國等國規范中最小剪力系數相關規定

一般來說，房屋結構底部的剪重比較小，上層的剪重比較大．因此，美國、歐洲、新西蘭等的設計規范中都對底部總剪力進行了控制．

美國規范UBC［3］規定設計基底總水平剪力的下限計算公式為：

式中：Ca為地震影響系數；I為結構的重要性系數；W為結構的總重力荷載代表值．

ASCE 7—05［4］對結構任意方向上的基底總剪力設計值規定為：

該規范同時給出了Cs的下限值為：

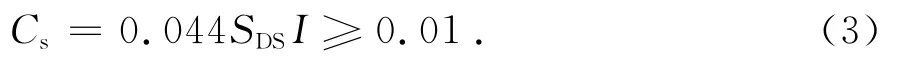
式中：Cs為基底剪力系數；SDS為5%阻尼比對應的設計反應譜周期0．2s對應的譜加速度．IBC［5］對最小基底總剪力的下限取值與ASCE 7－05相同．歐洲規范EN 1998－1［6］規定基底總剪力為：

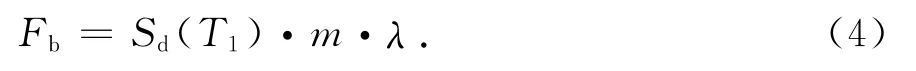
式中：λ為修正系數；Sd為設計反應譜，定義如下．

當0≤T≤TB時，

當TB＜T≤TC時，

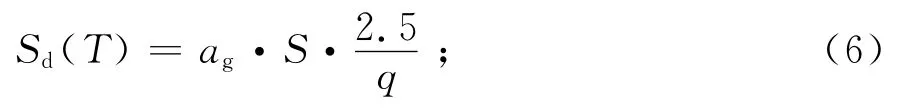
當TC＜T≤TD時，

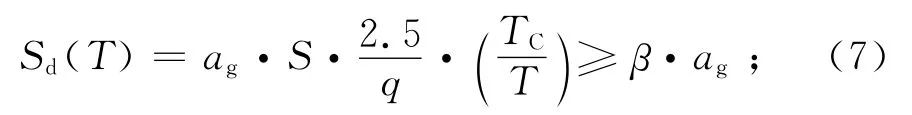
當TD＜T時，

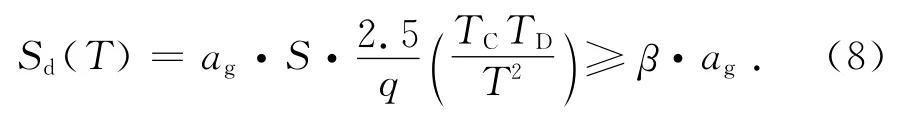
式中：ag為歐洲抗震規范A 類場地上475年重現期水準的地面峰值加速度；S為場地系數；TB為反應譜水平段對應周期的下限值；TC為反應譜水平段對應周期的上限值；TD為速度控制段與位移控制段的分界點對應的周期；q為結構性能系數；β為設計反應譜放大系數的下限值．

新西蘭規范NZS 1170．5：2004［7］對設計反應譜規定為：

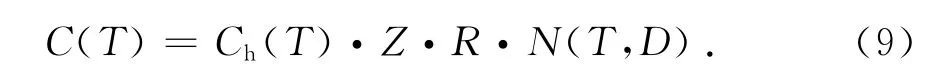
同時規定：

式中：Z為區域地震危險系數；R為50a超越概率10%時的地震反應修正系數；Ch（T）為反應譜系數．

1．2 中國規范中最小剪力系數相關規定

《建筑抗震設計規范》GB 50011—2010和《高層建筑混凝土結構技術規程》JGJ 3－2010中對樓層最小地震剪力系數值的規定是根據抗震驗算時，當結構扭轉效應明顯或基本周期小于3．5s時，地震剪力系數λ應不小于0．2αmax；當結構基本周期大于5．0s時，λ應不小于0．15αmax；基本周期介于3．5～5 s之間的結構，樓層最小地震剪力系數值λmin（表1）按插入法取值．

但是《建筑抗震設計規范》和《高層建筑混凝土結構技術規程》在剪重比取值的規定上存在以下主要問題［8－12］：

1）中國規范所規定的樓層最小地震剪力系數與場地類別無關，有悖于軟土場地上結構地震反應大于硬土場地上地震反應的一般規律．

2）同一棟建筑，建造在設防烈度低的地區時，剪重比有可能不能滿足規范要求．但是建造在設防烈度高的地區時，剪重比卻有可能滿足規范要求．

規范有關剪重比的規定還有待完善．

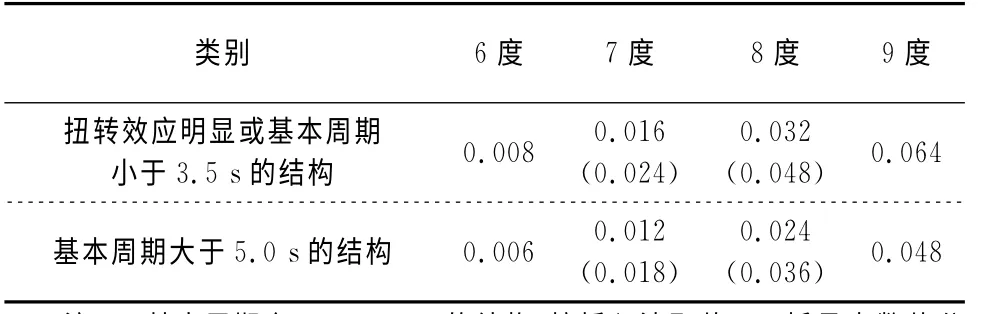
表1 樓層最小地震剪力系數值λminTab．1 The minimum story shear ratioλmin

本文研究我國規范規定的剪重比與結構基本周期之間的關系，從而通過建筑結構的自振周期就可以判斷該結構的剪重比是否滿足規范最小地震剪力系數的要求．

1．3 中國規范與美國等國規范中最小剪力系數相關規定的對比

中國規范和美國等國規范都對最小地震剪力系數的取值進行了規定，但是中國規范與美國等國的規范在具體的規定方面又有差別：

1）美國等國的規范對最小剪力系數是針對基底總剪力進行規定的，我國規范則是對層剪力進行規定的．

2）美國規范規定在按底部剪力法對結構進行計算設計時，其基底設計總剪力不能小于CsW，按振型分解法對結構進行設計計算時，其基底設計總剪力不能小于0．85CsW；我國規范無此明確規定．

3）美國等國規范規定的最小剪力系數大于等于0．01，我國規范規定的最小剪力系數λmin可小于0．01．

2 最小剪重比λmin與結構自振周期T的關系

現行《建筑抗震設計規范》（GB 50011—2010）和《高層建筑混凝土結構技術規程》（JGJ 3－2010）中對地震影響系數α的規定見圖1［1－2］．

圖1中，衰減指數按式（11）確定：

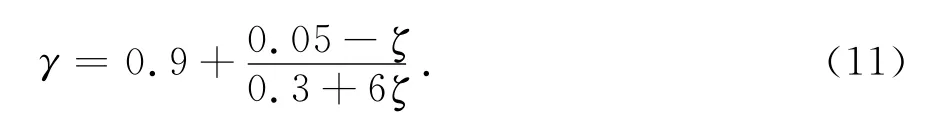
式中：ζ為阻尼比．

直線下降段的下降斜率調整系數按式（12）確定：

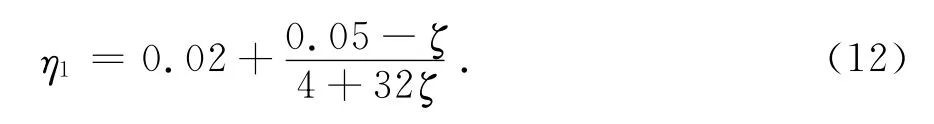
阻尼調整系數按式（13）確定：

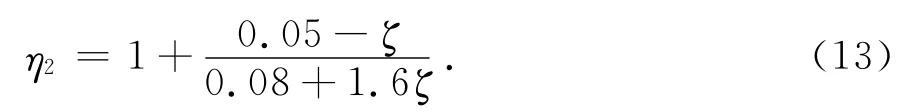
由圖1，式（11），式（12）和式（13）得到的地震影響系數α僅與特征周期Tg，結構自振周期T，地震影響系數最大值αmax和阻尼比ζ相關．其中地震影響系數最大值αmax取值見表2，特征周期Tg取值見表3［1－2］．

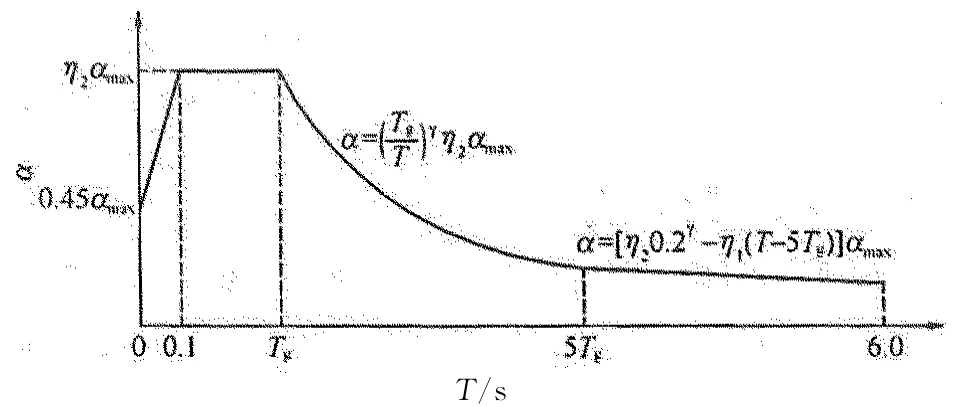
圖1 地震影響系數曲線Fig．1 Curves of seismic influence coefficient

如果將結構的基本周期遠大于5s定義為6s以上，參照表2可將地震影響系數下降段曲線分段，分段情況分為2種：

第1種情況：3．5s≤5Tg．此時，地震影響系數下降段曲線可分為T≤3．5s，3．5s＜T≤5Tg，5Tg＜T≤5s，5s＜T≤6s和T＞6s5段，如圖2所示．

第2種情況：5Tg＜3．5s．此時，地震影響系數下降段曲線可分為T≤5Tg，5Tg＜T≤3．5s，3．5s＜T≤5s，5s＜T≤6s和T＞6s5段，如圖3所示．

表2 水平地震影響系數最大值Tab．2 The maximum value of horizontal seismic influence coefficient

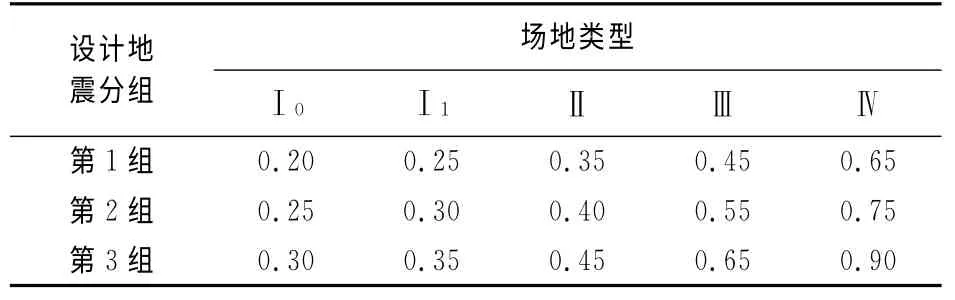
表3 特征周期值Tab．3 Characteristic period of site

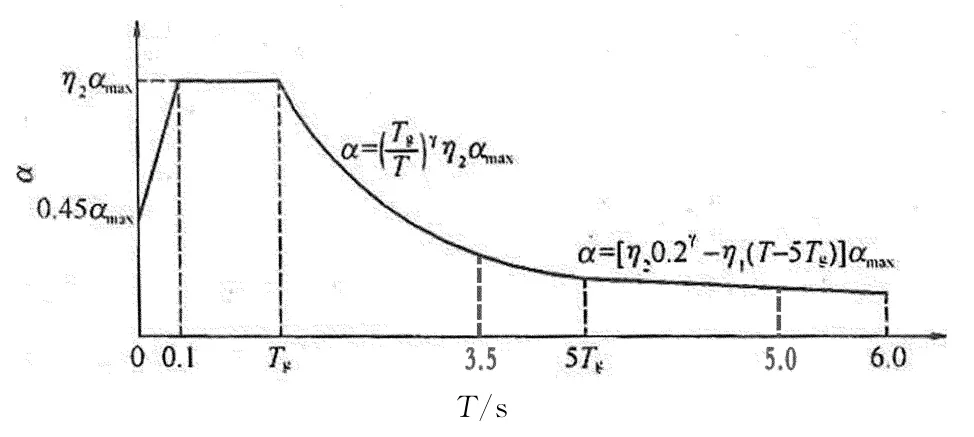
圖2 地震影響系數曲線第1種分段情況Fig．2 The first situation of seismic influence coefficient curves

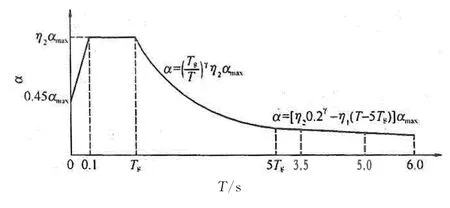
圖3 地震影響系數曲線第2種分段情況Fig．3 The second situation of seismic influence coefficient curves

3 滿足規范最小剪重比λmin要求的結構自振周期T 的推算

3．1 地震影響系數下降段曲線為第一種情況的推算

按多遇地震進行計算，地震影響系數下降段曲線為第一種情況時，因為3．5s≤5Tg，即Tg≥0．7 s，依據表2，與第Ⅳ類場地土的第二組和第三組設計地震分組情況對應，Tg分別為0．75和0．90．

第1段（T≤3．5s）：

從圖2 中可知，0＜T≤Tg時，α≥0．45αmax＞λmin，所以α＞λmin恒成立；Tg＜T≤3．5s時，

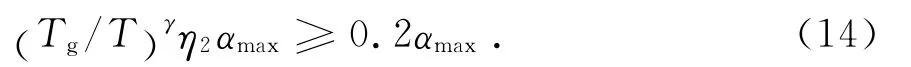
第2段（3．5s＜T≤5Tg）：

要使α≥λmin，所以要求

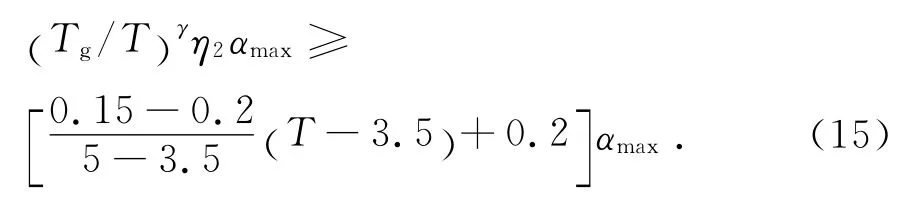
第3段（5Tg＜T ≤5s）：

要使α≥λmin，所以要求

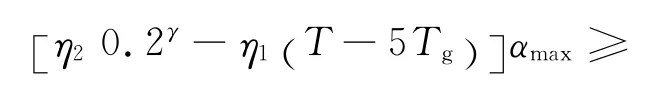
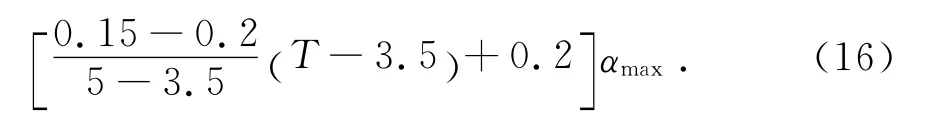
第4段（5s＜T≤6s）：

要使α≥λmin，所以要求

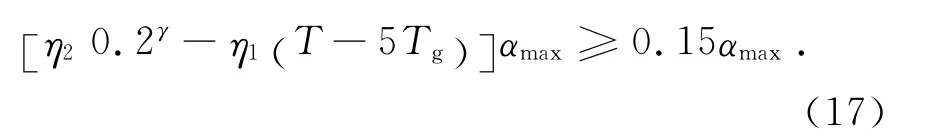
第5段（T＞6s）：

文獻［9］提出當結構的基本周期遠大于5s時，可以將結構的樓層最小地震剪力系數值減少15%，即為0．85×0．15αmax＝0．127 5αmax．該段樓層最小地震剪力系數值取85%折減系數，即λmin＝0．127 5 αmax．該段地震影響系數曲線方程與5Tg到6s段的地震影響曲線方程一樣，則要使α≥λmin，要求

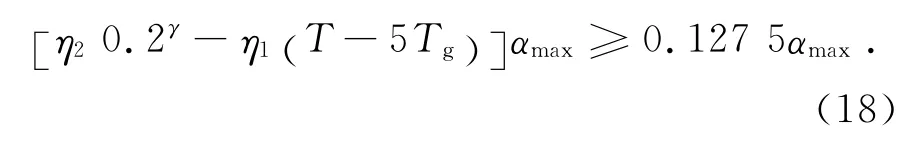
對式（18），因為當地震影響系數下降段曲線為第一種分段情況時（如圖2所示），Tg≥0．7s，對應于表3中的第Ⅳ類場地土的第二組和第三組設計地震分組情況，Tg分別為0．75和0．9．此時，按照規范要求對高層鋼結構、高層混合結構和高層混凝土結構的阻尼比ζ應分別取為0．02，0．04和0．05．

對式（14）～式（18）的計算結果進行合并匯總，得地震影響系數下降段曲線第一種分段情況下滿足規范剪重比要求的結構基本周期．

3．2 地震影響系數下降段曲線為第二種情況的推算

按多遇地震進行計算，地震影響系數下降段曲線第二種分段情況中每段的計算公式：

第1段（T≤5Tg）：

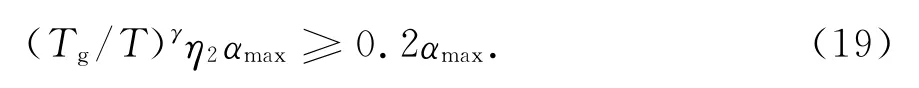
第2段（5Tg＜T≤3．5s）：

第3段（3．5s＜T≤5s）：

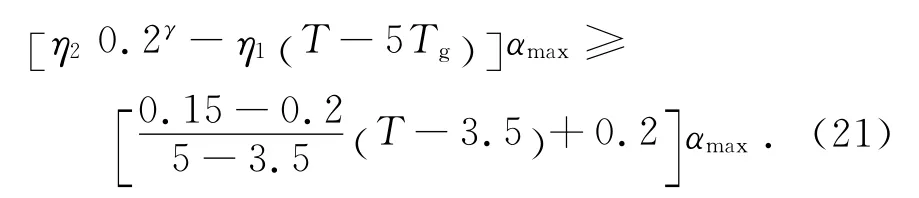
第4段（5s＜T≤6s）：

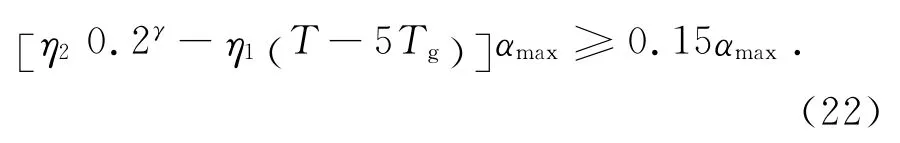
第5段（T＞6s）：

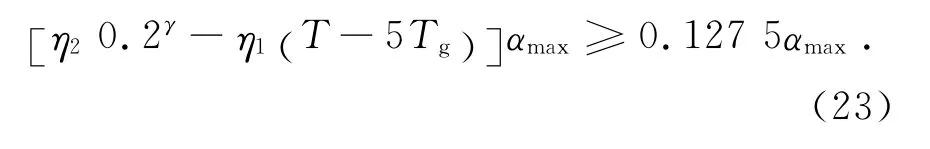
對式（19）～式（23）的計算結果進行合并匯總，得地震影響系數下降段曲線第二種分段情況下滿足規范剪重比要求的結構基本周期．

3．3 對兩種情況換算結果進行合并

對3．1節與3．2節的計算結果進行合并匯總可得滿足規范要求的樓層最小地震剪力系數值時結構基本周期的取值，見表4～表6．它們分別代表高層鋼結構、高層混合結構和高層混凝土結構滿足規范最小地震剪力系數要求時的結構基本周期．

4 工程實例驗證

本文搜集選取了一些有代表性的高層建筑的相關信息，見表7，對表4～表6進行驗證．驗證了當結構的周期在表4～表6內所示的區間時，該結構的剪重比能滿足規范對剪重比的限值要求，證明了本文推導公式的正確性．

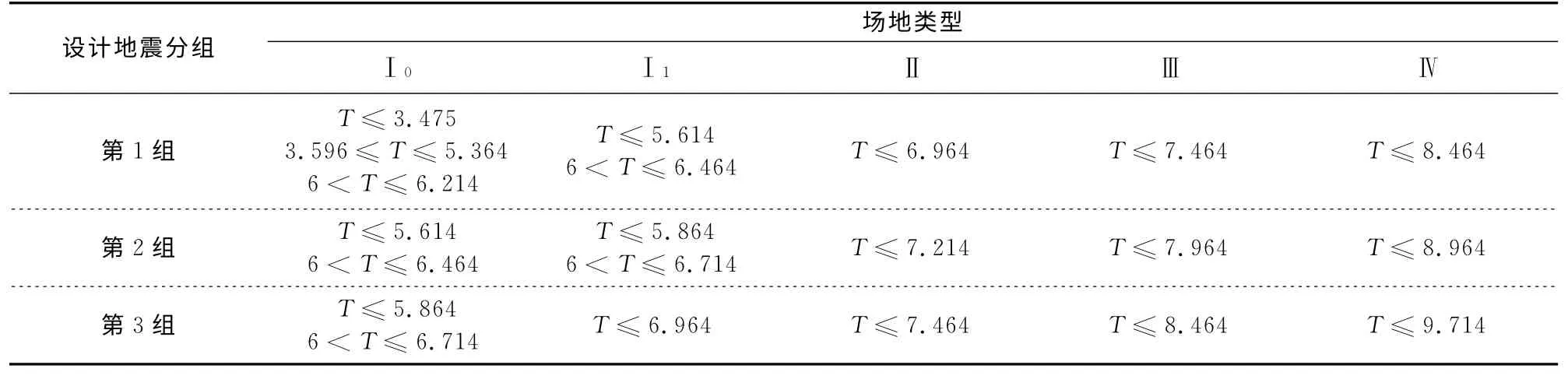
表4 阻尼比ζ＝0．02時符合規范最小地震剪力系數要求的基本周期TTab．4 Basic structural period satisfied with shear－gravity ratio of the codes when damping ratio is 0．02 s

表5 阻尼比ζ＝0．04時符合規范最小地震剪力系數要求的基本周期TTab．5 Basic structural period satisfied with shear－gravity ratio of the codes when damping ratio is 0．04 s

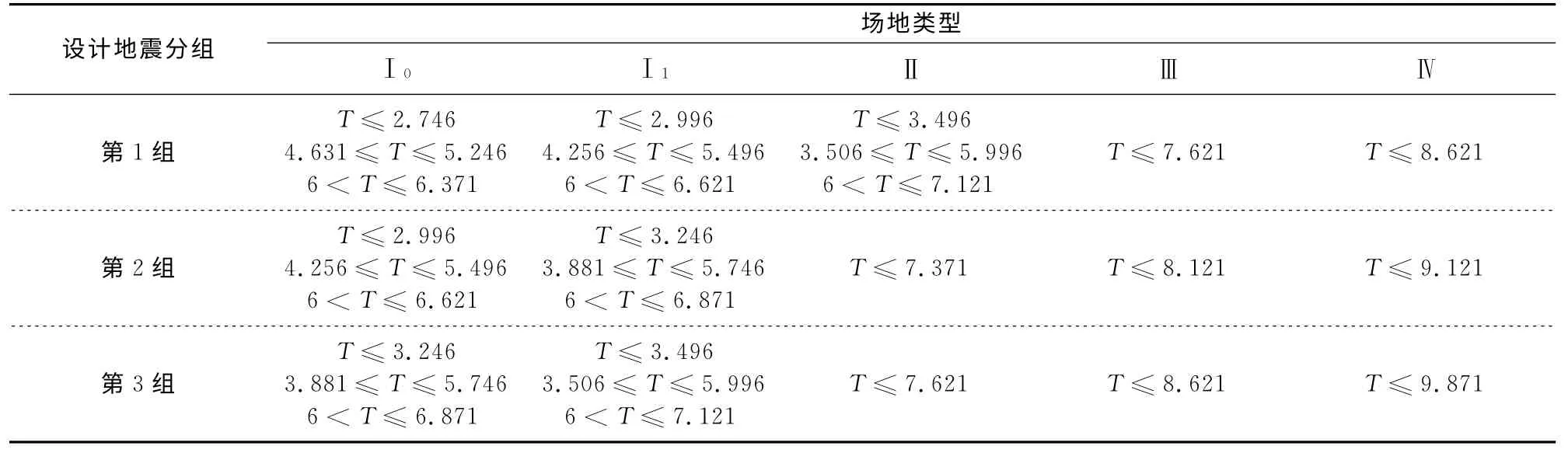
表6 阻尼比ζ＝0．05時符合規范最小地震剪力系數要求的基本周期TTab．6 Basic structural period satisfied with shear－gravity ratio of the codes when damping ratio is 0．05 s

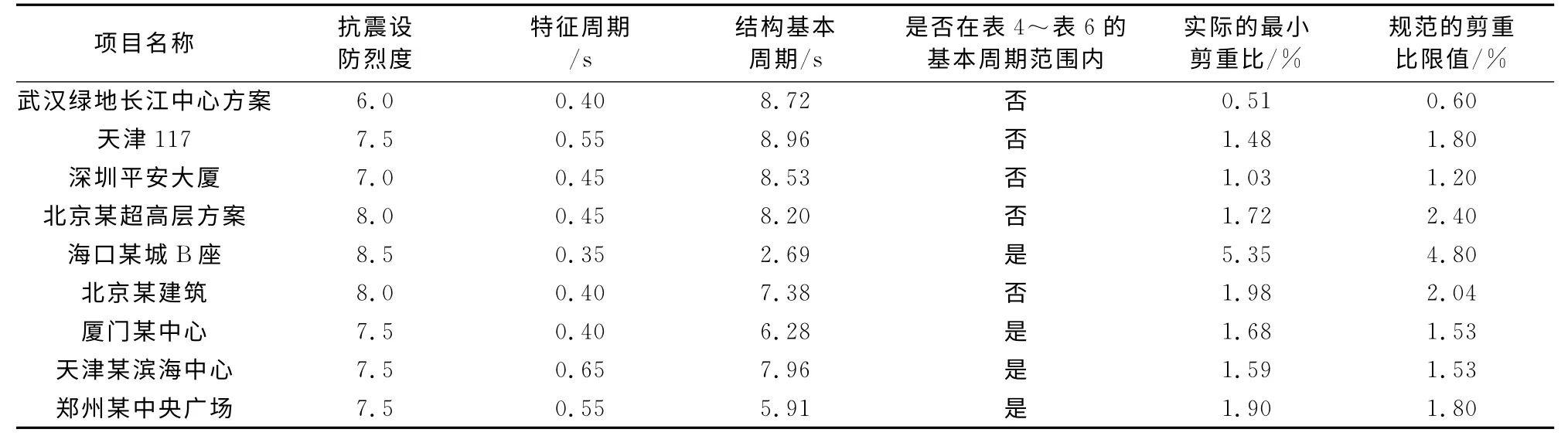
表7 工程實例中剪重比與其他參數Tab．7 Shear－gravity ratio and other parameters in example tall buildings

5 結 論

基于《建筑抗震設計規范》（GB 50011—2010）與《高層建筑混凝土結構技術規程》（JGJ 3－2010）對結構的最小地震剪力系數值的要求，對符合現行抗震規范地震剪力系數要求的高層結構基本周期進行分析，得到以下結論：

1）由于我國規范人為規定的最小剪重比與結構的自振周期有關，因此，根據結構的自振周期值便可以初步判斷結構的剪重比是否滿足規范的要求．

2）當高層建筑結構的剪重比能滿足規范的最小剪重比要求時，結構的基本自振周期均滿足表4～表6的要求；若結構的自振周期不在表4～表6所示的區間中，則該結構的剪重比一定不滿足我國規范對剪重比的要求．

3）由表4～表6可見，在滿足規范剪重比要求的結構自振周期最大值的區間內，有可能出現不滿足規范剪重比要求的自振周期區段．

［1］GB 50011—2010 建筑抗震設計規范［S］．北京：中國建筑工業出版社，2010：33－39．

GB 50011—2010Code for seismic design of buildings［S］．Beijing：China Architecture ＆Building Press，2010：33－39．（In Chinese）

［2］JGJ 3—2010 高層建筑混凝土結構技術規程［S］．北京：中國建筑工業出版社，2010：36－41．

JGJ 3－2010Technical specification for concrete structures of tall building［S］．Beijing：China Architecture ＆ Building Press，2010：36－41．（In Chinese）

［3］UBC．Uniform building code：Volume 2［S］．Whittier，California：International Conference of Building Officials，1997：14－24．

［4］ASCE 7—05 Minimum design loads for buildings and other structures［S］．Reston，Virginia：American Society of Civil Engineers，2005：129．

［5］IBC．International building code［S］．Falls Church，Virginia：International Code Council，2006：302－307．

［6］EN 1998－1Design of structures for earthquake resistance：part 1：general rules seismic actions and rules for buildings［S］．London：BSI，2004：56－57．

［7］NZS 1170．5：2004Structural design actions：part 5：earthquake actions［S］．Wellington，New Zealand：Standards New Zealand，2004：10－21．

［8］廖耘，容柏生，李盛勇．剪重比的本質關系推導及其對長周期超高層建筑的影響［J］．建筑結構，2013，43（5）：1－4．

LIAO Yun，RONG Bai－sheng，LI Sheng－yong．Derivation of shear－gravity ratio and its effect on long－period super high－rise buildings［J］．Building Structure，2013，43（5）：1－4．（In Chinese）

［9］汪大綏，周建龍，姜文偉，等．超高層結構地震剪力系數限值研究［J］．建筑結構，2012，42（5）：24－27．

WANG Da－sui，ZHOU Jian－long，JIANG Wen－wei，etal．Research on seismic shear gravity ratio limit for super high－rise buildings higher than 500m［J］．Building Structure，2012，42（5）：24－27．（In Chinese）

［10］方小丹，魏璉．關于建筑結構抗震設計若干問題的討論［J］．建筑結構學報，2011，32（12）：46－51．

FANG Xiao－dan，WEI Lian．Discuss on issues of seismic design of building structures［J］．Journal of Building Structures，2011，32（12）：46－51．（In Chinese）

［11］方小丹，魏璉，周靖．長周期結構地震反應的特點與反應譜［J］．建筑結構學報，2014，35（3）：16－23．

FANG Xiao－dan，WEI Lian，ZHOU Jing．Characteristics of earthquake response for long－period structures and response spectrum［J］．Journal of Building Structures，2014，35（3）：16－23．（In Chinese）

［12］王國弢，胡克旭，周禮奎．位移譜阻尼調整系數模型研究［J］．湖南大學學報：自然科學版，2014，41（11）：48－57．

WANG Guo－tao，HU Ke－xu，ZHOU Li－kui．Study on damping scaling factor model for displacement response spectra［J］．Journal of Hunan University：Natural Sciences，2014，41（11）：48－57．（In Chinese）