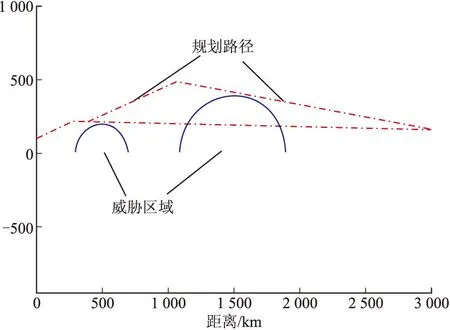
基于Dubins曲線的高超聲速飛行器路徑規劃*

王荔豪,王愛華,柯　楠,于云峰

(1　西北工業大學航天學院,西安　710072;2　上海航天技術研究院,上海　200245;

3　西北工業大學軟件與微電子學院,西安　710072)

基于Dubins曲線的高超聲速飛行器路徑規劃*

王荔豪1,王愛華2,柯楠3,于云峰1

(1西北工業大學航天學院,西安710072;2上海航天技術研究院,上海200245;

3西北工業大學軟件與微電子學院,西安710072)

摘要:對于高超聲速飛行器而言,在進行航跡規劃時需要考慮很多的約束條件,主要的約束條件是有限的轉彎半徑和最短的飛行路徑。針對這些問題,文中設計了一種基于Dubins曲線的高超聲速飛行器路徑規劃算法,并對算法的通用性進行了仿真分析。結果表明,本算法能夠為飛行器在起始位置和終止位置之間規劃出一條滿足約束條件的最短飛行軌跡,并且能夠避開雷達探測、激光武器威脅、電子干擾威脅等威脅區域。

關鍵詞:高超聲速飛行器,Dubins曲線;約束條件;路徑規劃

0引言

高超聲速飛行器是指在大氣層內以大于5Ma速度飛行的一類飛行器,與傳統飛行器相比,具備遠程快速打擊能力,能夠適應未來快節奏作戰需要。同時,由于全局飛行環境無法準確預知,所以需要實時的規劃飛行軌跡,來避開已知的威脅區域以及新出現的威脅[1]。文獻[2]基于A*算法,對低空飛行器進行實時航跡規劃,取得了較好的效果,但是由于高超聲速飛行器的飛行高度高的特點,此方法不適用于高超聲速飛行器的航跡規劃。文獻[3]提出了一種基于A*算法的三維航跡規劃算法,通過離散飛行器過載來構建搜索空間,但是這種方法在節點擴散時的計算量過大,影響規劃效率。文獻[4]提出一種基于改進稀疏A*算法的高超聲速飛行器航跡規劃技術,能夠有效的避開各種威脅,但沒有針對性地對飛行器最短路徑進行研究。

文中在Dubins曲線規劃基礎上,設計用于高超聲速飛行器的路徑規劃算法,隨后建立威脅場模型,并進行仿真分析。結果表明,本算法能夠為高超聲速飛行器在起始位置和目標位置之間規劃出一條最短飛行路徑,所規劃路徑綜合考慮了飛行器的轉彎半徑要求和到達目標位置的角度要求,并在飛行過程中避開雷達探測、激光武器威脅、電子干擾威脅等威脅區域,且算法運算速度快,穩定性較好。

1約束條件

高超聲速飛行器航跡規劃的目的是要尋找一條保證飛行器安全突防的飛行軌跡,需要盡量減少被敵方捕獲和摧毀的概率。同時,為高超聲速飛行器規劃的路徑既要滿足飛行器本身的物理機動性能,又需要滿足一系列約束條件。一般來說,約束條件包括以下幾個方面:

1)最大轉彎角。由于高超聲速飛行器多采用機體/發動機一體化設計理論,決定了其機動能力較差,轉彎半徑較大,生成的飛行軌跡只能在小于或等于預先確定的最大角度范圍內轉彎。該約束條件也取決于具體飛行器的性能和飛行任務。

2)航跡距離約束。飛行器的航跡距離約束與其飛行高度、飛行路徑長度、機動次數等因素密切相關。由于受到飛行器燃料供應量的限制,航跡長度必須小于或等于預先設定的最大距離,同時要求飛行路徑越短越好,這樣能夠保證飛行器在固定的時間內必須到達目標所在位置。

3)最小航跡段長度。其限制了飛行器在開始改變飛行姿態前必須直飛的最短距離。保證飛行器在遠距離飛行時不進行迂回和頻繁的轉彎。

4)固定的目標進入方向。確保飛行器從特定的角度接近目標,從而對目標的最薄弱位置進行有效攻擊。

2威脅建模

高超聲速飛行器作戰區域廣,飛行區域內分布有各種威脅。在航跡規劃過程中需要考慮的威脅主要有雷達、激光、電子干擾等威脅場。

2.1　雷達威脅

對于飛行器是否被探測到,即是否仍對雷達處于隱身狀態是以一定的發現概率為條件的[5]。這里將雷達探測概率計算模型簡化為:

(1)

式中:Rmax為雷達最大作用距離;r為雷達與飛行器之間的水平距離。

2.2　激光武器威脅

對于飛行器的航跡規劃研究,激光武器的殺傷范圍定義為一個以武器發射裝置為球心的半球形的區域,如圖1所示。

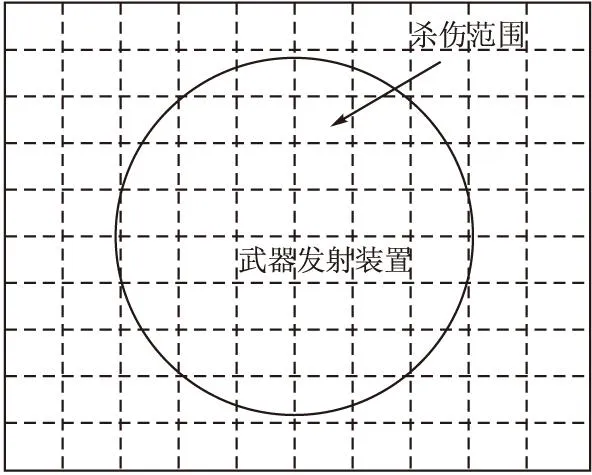
圖1　激光武器威脅范圍示意圖

2.3　電子干擾威脅

一般情況下,認為電子干擾的作用范圍為半球形,構成了以電子干擾發射裝置位置為中心,以最大作用范圍為半徑的威脅區域。

3路徑規劃

路徑規劃是飛行器任務飛行的關鍵組成部分。需要根據任務目標規劃出滿足約束條件的飛行軌跡,在起始位置和目標位置之間自動生成一條最優的飛行軌跡,從而使飛行器能夠以最短的時間到達目標所在位置,安全可靠的完成預定飛行任務。

3.1　Dubins曲線

假設空間有兩個位置點Pi=(xi,yi,θi)和Pf=(xf,yf,θf),下標i表示起始位置的參數,f表示目標位置的參數,它們分別為飛行器的起始位置和目標位置,之間的距離遠大于2Rturn,其中Rturn為飛行器轉彎時的轉彎半徑,且滿足Rturn≥Rmin,Rmin為飛行器的最小轉彎半徑。

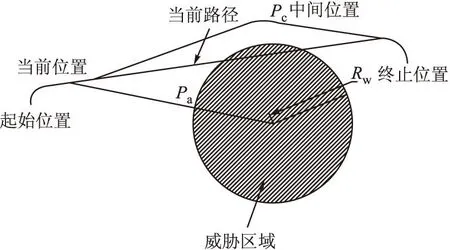
基于Dubins理論,在起始位置和目標位置之間可以規劃出一條滿足約束條件的最短飛行路徑,如圖2所示。

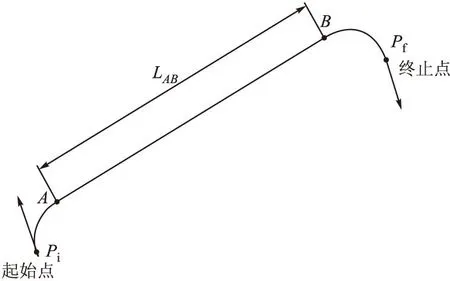
圖2　Dubins最短飛行路徑示意圖

3.2　避障策略

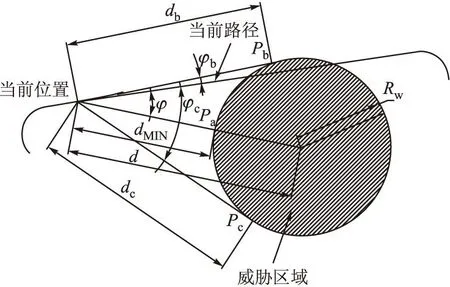
1)威脅區域阻擋判定

將威脅區域的中心定義為威脅點,在飛行器的飛行過程中,如果滿足d·sin|φ|

(2)

式中:xw和yw為威脅點的位置;xd和yd為當前飛行器所在位置。

(3)

式中:β為當前飛行速度與水平方向的夾角。

2)避障方法

在飛行器飛行過程中,如果判斷威脅區域覆蓋了當前路徑,按照以下方法對飛行路徑進行重新規劃。

i)生成中間位置坐標(xc,yc)

當飛行器在飛行過程中計算判斷到威脅區域覆蓋了當前路徑時,計算得到飛行器當前位置與威脅區域之間的最短距離,記為dmin。

(4)

式中:Rw為威脅區域的半徑,此時威脅區域形狀在二維平面以圓形計算。

最短距離所對應的威脅區域邊界點記為Pa,定義該連線與飛行器當前速度方向的夾角為φa;同時定義飛行器當前位置距離威脅區域兩個最邊緣的邊界點分別為Pb和Pc,其與當前位置的距離分別為db和dc,得到:

(5)

它們的連線與飛行器當前速度方向夾角分別記為φb和φc,如圖3所示。

圖3　具體參數示意圖

以飛行器當前位置為起點,d=dmin為矢量長度,以飛行器當前速度方向為基準方向,旋轉一個角度θ,得到一個矢量,其中θ的計算方法如下:

(6)

式中:Δθ為預設定的角度步長;m=1,2,…,π/Δθ。

計算矢量dmin·sin|θ-φn|,如果滿足:

(7)

則該矢量的終點坐標即為飛行器中間位置的坐標。否則以飛行器當前速度方向為基準方向,旋轉-θ角度生成矢量,若該矢量滿足上式,則該矢量的終點坐標即為飛行器中間位置的坐標;否則令m=m+1,重復上述過程,直至生成的矢量滿足上式;經過多次迭代后,如果m取值大于π/Δθ,則改變矢量長度d,令d=α·d,0<α<1,此時重新選取m=1,重復前面的求取過程,直至生成矢量滿足上式。

經過上述迭代計算后,如果飛行器當前位置為(xw,yw,θw),則中間位置的坐標為:

(8)

式中d和θ都是經過迭代過程后的最終取值。

ii)生成中間位置的方向角度θc

在計算了中間位置的坐標后,還需要計算飛行器到達中間位置的方向。首先從當前位置到中間位置規劃出一條Dubins路徑,這條路徑包括直飛距離和中間位置的圓弧距離。所以,計算中間位置的方向時,可以直接令中間位置的方向指向終止位置的兩個切圓中距離較近的那個切圓的切線,這樣在計算由中間位置到終止位置間的Dubins路徑時,就不需要計算中間位置的切圓,生成的飛行路徑僅由一條切線和終止位置的切圓圓弧組成,如圖4所示。

圖4　飛行器避障示意圖

中間位置的方向角度為:

(9)

式中:Rturn為飛行器的轉彎半徑,終止切圓圓心坐標為(xO2,yO2)。

3)總結

文中首先定義飛行器的起始位置Pi和目標位置Pf,規劃出一條Dubins路徑。飛行器從起始位置飛行開始,當飛行器飛行了一段最小航跡段后,開始對威脅區是否覆蓋當前飛行路徑進行判斷。如果判斷威

脅區沒有覆蓋飛行路徑后,則沿該路徑一直飛行,在飛行過程中每飛行一定距離后計算一次,實時判斷威脅區是否覆蓋當前飛行路徑。

當飛行器飛行至當前位置時,如果計算判斷到威脅區域覆蓋了當前路徑,則需要采用避障策略為飛行器計算生成一個中間位置Pc,同時實時規劃出一條從當前位置到中間位置Pc之間的Dubins路徑,之后飛行器將沿新生成的路徑飛行至Pc處。在飛行器到達中間位置Pc后,會重新規劃出一條從中間位置Pc到目標位置Pf的Dubins路徑,將該路徑作為飛行器的當前飛行路徑。

在新生成的路徑飛行過程中,不斷重復以上計算判斷過程,直至飛行器到達目標位置Pf。

4仿真分析

圖5　仿真結果示意圖

仿真區域設置為3 000 km×500 km,設有兩處威脅場,威脅范圍半徑分別為200 km和400 km,飛行器轉彎半徑設置為20 km,使用Matlab軟件實現仿真過程。如圖5所示,為仿真得到的飛行器飛行路徑規劃圖,路徑規劃區域水平寬度為3 000 km,規劃區域高度為500 km。從圖中可以看出,所規劃的飛行路徑能夠滿足飛行器的轉彎半徑約束條件,并且保證了最短的飛行距離,同時有效的避開了設置的威脅場。另外,在仿真過程中還發現,對于文中所列兩個威脅場的情況,完成飛行器飛行路徑規劃總共用時0.04 s,運算速度快,且穩定性較好。

5結論

文中首先分析了高超聲速飛行器與普通飛行器在航跡規劃技術方面的不同之處,并有針對性地建立了威脅場模型,隨后在Dubins曲線的基礎上,設計了一種用于高超聲速飛行器的路徑規劃避障算法,最后對該算法的通用性進行了Matlab仿真分析。仿真結果表明:該算法能夠實時為飛行器規劃出一條最短飛行路徑,且規劃時間短,同時能有效的避開威脅區域。

參考文獻:

[1]鄭昌文. 飛行器航跡規劃研究 [J]. 宇航學報, 2007, 28(6): 1441-1446.

[2]管文艷, 韓亮. 低空突防模型建模的研究 [J]. 系統仿真學報, 2006, 18(2): 77-82.

[3]宋建梅, 李侃. 基于A*算法的遠程導彈三維航跡規劃算法 [J]. 北京理工大學學報, 2007, 27(7): 613-617.

[4]孟中杰, 黃攀峰, 閆杰. 基于改進稀疏A*算法的高超聲速飛行器航跡規劃技術 [J]. 西北工業大學學報, 2010, 28(2): 182-186.

[5]郭正新, 江晶. 一種不同距離的雷達檢測概率計算模型 [J]. 空軍雷達學院學報, 2003. 17(4): 7-9.

收稿日期:2015-03-04

作者簡介:王荔豪(1991-),男,陜西渭南人,碩士研究生,研究方向:飛行器控制與仿真研究。

中圖分類號:TP319.9

文獻標志碼:A

Route Planning for Hypersonic Vehicle Based on Dubins Curves

WANG Lihao1,WANG Aihua2,KE Nan3,YU Yunfeng1

(1School of Astronautics, Northwestern Polytechnic University, Xi’an 710072, China;

2Shanghai Academy of Spaceflight Technology, Shanghai 200245, China;

3School of Sofeware and Microelectronics, Northwestern Polytechnic University, Xi’an 710072, China)

Abstract:So many constraint conditions should be considered when planning route for hypersonic vehicle. The most important constraint conditions are the limited radius of turning circle and the shortest flight route. A flight path planning method based on Dubins geometric method for hypersonic vehicle was designed, then simulating and analysising the generality of algorithm. What is indicated in the result is that this algorithm can plan a shortest flight path meeting the constraint conditions between initial point and termination point for vehicle. This path can avoid the deterrent of radar, laser weapons, and electronic interfence.

Keywords:hypersonic vehicle; constraint condition; route planning