一種高度二階可導的機載巡飛彈大空域降高彈道設計方法*

車曉濤,王　蕭,郝　峰,李海城,孫虎元

(1　中國兵器工業第203研究所,西安　710065;2　解放軍邊防學院,西安　710108)

一種高度二階可導的機載巡飛彈大空域降高彈道設計方法*

車曉濤1,王蕭1,郝峰1,李海城1,孫虎元2

(1中國兵器工業第203研究所,西安710065;2解放軍邊防學院,西安710108)

摘要:機載巡飛彈在大空域降高彈道起點和終點會出現彈體抖動和過渡時間過長的現象。文中分析了高度連續和速度連續的兩類降高方案彈道產生這種現象的物理原因,從彈道優化設計的角度提出了一種垂向加速度連續的降高彈道設計方法。該方法可在不改變控制系統復雜度的情況下,實現降高彈道的平穩快速過渡,并減小降高段末端的高度沖出量。彈道仿真結果表明,該方法改進效果明顯,可以為機載巡飛彈及其他類似彈藥的彈道設計提供參考。

關鍵詞:機載巡飛彈;大空域降高;方案彈道;彈道優化

0引言

機載巡飛彈是一種新型空對地精確打擊武器。它一般由載機從10~20 km的高空投放,經過無動力降高/滑翔進入目標區域,隨后在目標區域上方200~500 m高度進行有動力的“巡弋飛行”,執行偵察和精確打擊任務[1]。為了保證巡飛彈在降高段末端能夠快速穩定的轉入巡飛偵察段,對其大空域降高彈道的設計顯得尤為重要。

目前國內外在降高方案彈道設計方面一般采用指數形式的高度連續方案或三角函數形式的速度連續方案,在降高段的起點和終點保證高度、垂向速度的連續[2-7]。這些方案由于降高段與前后兩段彈道切換點處的垂向加速度不連續,控制系統為了響應垂向加速度的跳變,產生跳變的需用舵控指令,最終導致降高彈道起點和終點巡飛彈的姿態、攻角等產生振動,過渡時間變長,并且在降高段終點,高度沖出量大大增加。這些問題雖然可以通過增加俯仰阻尼、角速度阻尼或對控制指令進行平滑處理等措施得到部分改善,但是增加了控制系統復雜度,并且沒有從本質上消除產生彈體振動和高度沖出量的原因。

針對以上問題,文中從彈道優化設計的角度提出了一種垂向加速度連續的降高彈道設計方法,對現有降高方案彈道進行改進,保證了機載巡飛彈所受合力垂向分量的平滑過渡,從物理本質上消除了彈體振動和高度沖出量產生的原因。

1一般降高方案彈道的分析

文中研究過程中設定巡飛彈開始處于高空平飛彈道,高度H0=10 000 m,速度268 m/s,低空巡飛高度H1=500 m;從t0=150 s開始降高,t1=230 s時轉入低空巡飛彈道,降高過程持續80 s。

一般降高方案彈道采用指數形式的高度連續或三角函數形式的速度連續方案,在降高段的起點和終點保證高度、速度的連續。將其歸納為以下兩類分別進行分析。

1.1　高度連續(零階可導)的降高方案

指數形式的降高方案使彈道銜接點處高度連續,飛行高度按規劃的指數函數值變化,但高度的一階和二階導數即垂向速度和垂向加速度不連續,表達式如下:

(1)

式中:t0、t1為設定的降高段起點和終點時間;A、B、k為計算所得控制參數[2,7]。

針對上文規定的巡飛彈飛行狀態,求得滿足式(1)的參數如下:k=0.028 23,A=10 000,B=-602.3。

從圖1~圖3可以看出,上述指數形式彈道的高度連續,但在t0時刻垂向速度和加速度都很大并且持續較長時間,其中vn0≈-300 m/s,an0≈8.49 m/s2。一般巡飛彈無法瞬間產生這么大的過載,導致控制系統無法跟蹤所設計的彈道。因此,針對上述彈道存在的缺陷,文中設計了另一種形式的由兩段指數函數組成的降高彈道,其表達式為:

(2)

式中變量意義同式(1)。求得一組參數為:A=10 417.6,B=-82.42,k=0.062 89。則高度、垂向速度、垂向加速度曲線如圖1~圖3所示。

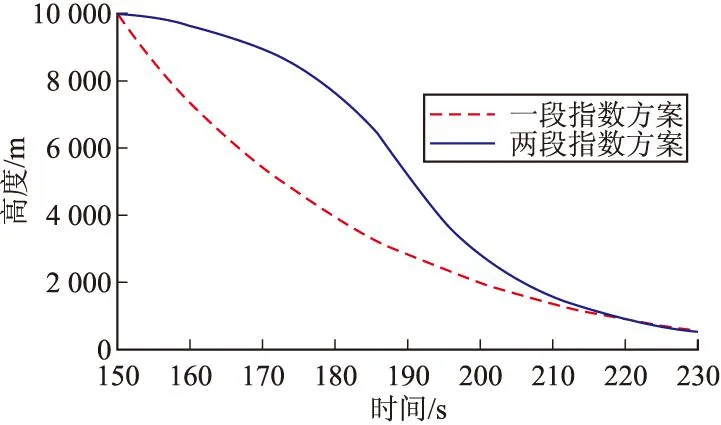
圖1　零階方案高度曲線

圖2　零階方案垂向速度曲線

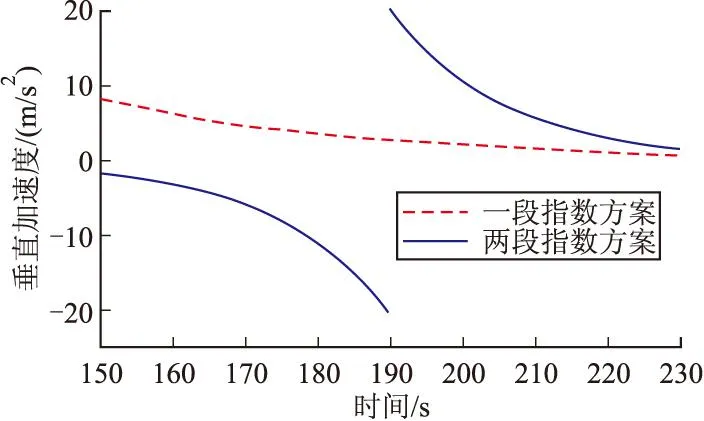
圖3　零階方案垂向加速度曲線

可以看出,相比一段指數函數形式的彈道,兩段指數函數形式的彈道在t0、t1時刻的垂向速度、加速度均減小了很多,更易于控制系統的控制。

1.2　高度一階可導的降高方案

高度一階可導的三角函數降高方案使彈道銜接點處高度和垂向速度連續,但垂向加速度不連續。一般表達式為:

(3)

式中A、ω、φ、B為待求的方案彈道參數。可根據降高段起點和終點的高度H0、H1,速度vn0、vn1,令y(t0)=H0,y(t1)=H1,y′(t0)=vn0,y′(t1)=0,列出如下非線性方程組進行解算:

(4)

求解得到:A=-4 750.0,ω=0.039 27,φ=-1.571,B=5 250.0。則高度、垂向速度、垂向加速度曲線如圖4~圖6所示。

圖4　一階方案高度曲線

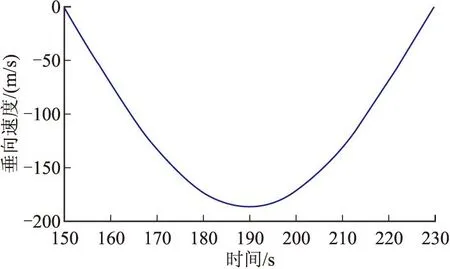
圖5　一階方案垂向速度曲線

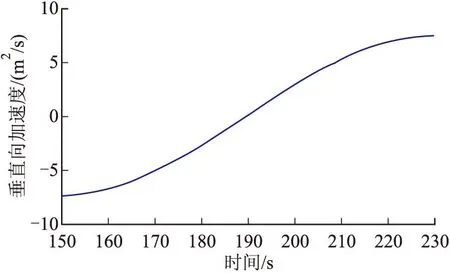
圖6　一階方案垂向加速度曲線

1.3　對一般降高方案存在不足的分析

高度的二階導數為垂向加速度,根據牛頓第二定律:F=ma可知,垂向加速度與作用在彈體上的合力垂向分量成比例。而以上兩類方案彈道在彈道銜接點處的垂向速度或垂向加速度存在跳變,控制系統為了響應其跳變,產生跳變的需用舵控指令,最終造成了彈道銜接點處巡飛彈姿態、攻角、彈道傾角等的振動,銜接點過渡時間變長,并且在降高段終點,高度沖出量增加。因此,為了保證彈道銜接點處的平穩過渡,除了使得方案彈道的高度連續,還應保證其垂向速度、垂向加速度的連續。下文的計算機仿真可以驗證這個分析。

2改進的方案彈道設計方法

為了改進一般降高方案存在的不足,文中從彈道優化的角度提出了一種垂向加速度連續即高度二階可導的降高方案彈道設計方法。該設計方法的核心在于通過參數設計使得t0和t1這兩個彈道銜接點處的垂向加速度an連續,從而使得飛行狀態平穩過渡,從物理本質上消除了彈體抖動的成因。

該設計方法的設計步驟如下:

1)列寫擬采用降高方案的高度方案y=f0(t),對此表達式進行一次和二次求導得到垂向速度y′=f1(t)、垂向加速度y″=f2(t)的表達式。

2)分析y=f0(t),y′=f1(t),y″=f2(t)中包含的待求解參數x0,x1,…,xN,參數個數N應滿足N≤6,否則,轉至步驟1)重新設計。

3)確定降高段起點和終點的高度H0、H1,時間t0、t1,根據巡飛彈轉入降高段時刻的彈道參數實時獲得起點垂向速度vn0、垂向加速度an0,期望的終點vn1、an1(一般均為零)。

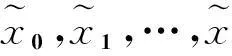
6)計算機仿真驗證分析。

3高度二階可導的降高方案

應用上面提出的降高方案彈道設計方法對三角函數形式的降高方案進行改進,得到一個文中設計方法的實例。使彈道銜接點處巡飛彈的高度、垂向速度和垂向加速度均連續,則高度、垂向速度、垂向加速度應滿足:

(5)

式中A、ω、φ、B、C、D為待求的方案彈道參數。

要解出A、ω、φ、B、C、D六個量,可根據降高段起點和終點的高度H0、H1,垂向速度vn0、vn1,垂向加速度an0、an1,令y(t0)=H0,y(t1)=H1,y′(t0)=vn0,y′(t1)=0,y″(t0)=an0,y″(t1)=0,列出如下非線性方程組:

(6)

降高彈道起點垂向加速度一般小于等于零,且其絕對值小于降高過程中垂向加速度絕對值的最大值,由此得到約束條件,即參數取值范圍為:

(7)

采用信賴域折線算法解得一組滿足要求的參數:A=1 512.0,ω=-0.078 54,φ=3.141 6,B=-3.29 6e-17,C=-118.6,D=27 813。則方案彈道的高度、垂向速度、垂向加速度曲線如圖7~圖9所示。

圖7　二階方案高度曲線

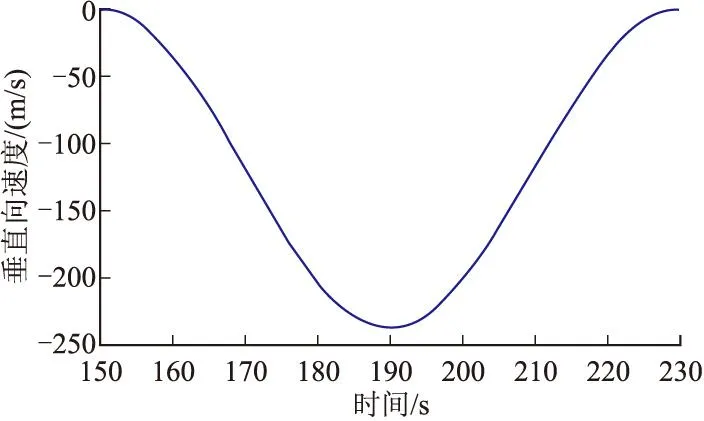
圖8　二階方案垂向速度曲線

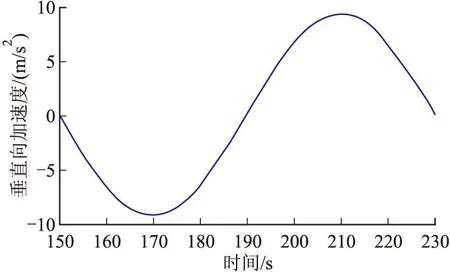
圖9　二階方案垂向加速度曲線

4仿真分析

對于同一方案彈道,不同復雜度的控制模型會對結果有不同程度的影響。文中重點分析降高方案彈道的優劣,因此采用最簡單的PID控制器對巡飛彈俯仰運動進行控制,對于文中涉及的所有方案均采用完全相同的控制參數和控制結構。控制模型為:

(8)

式中:δz為俯仰舵控制指令;Kp=0.8,Ki=0.45,Kd=0.15分別為PID控制器的比例、積分、微分系數;h(t)、hc(t)分別為t時刻巡飛彈的實際高度和方案彈道期望高度;v(t)、vc(t)為實際垂向速度和期望垂向速度。

控制系統框圖如圖10所示。

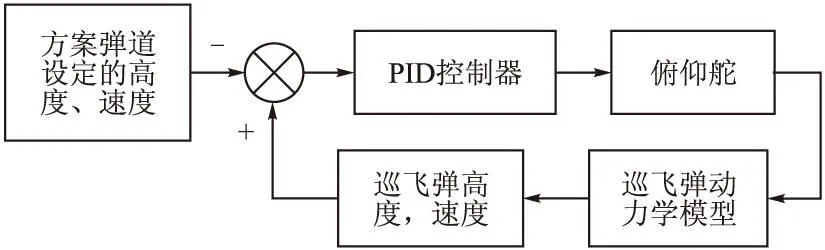
圖10　文中控制系統框圖

對上面提到的3種方案進行計算機仿真,得到如圖11~圖14的結果。

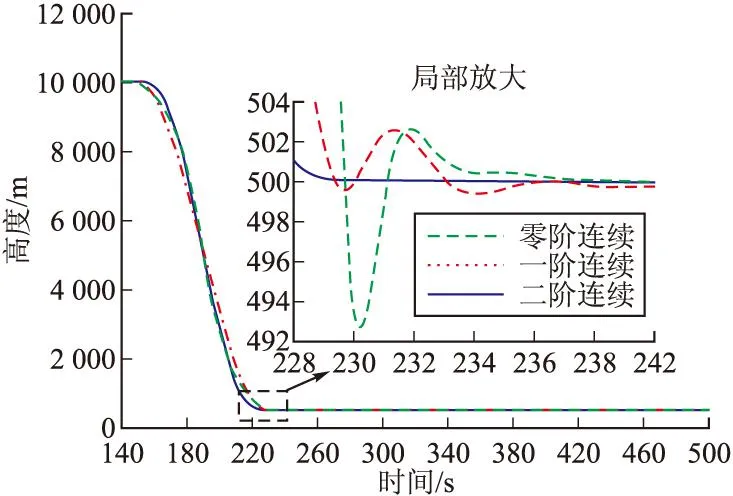
圖11　高度隨時間變化仿真結果

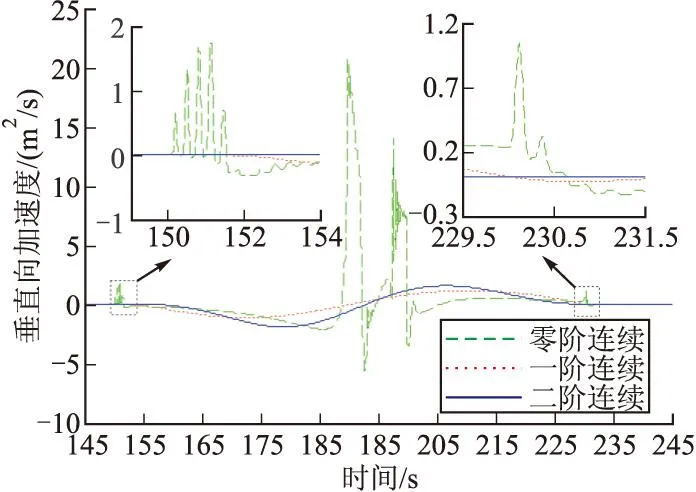
圖12　垂向加速度隨時間變化仿真結果

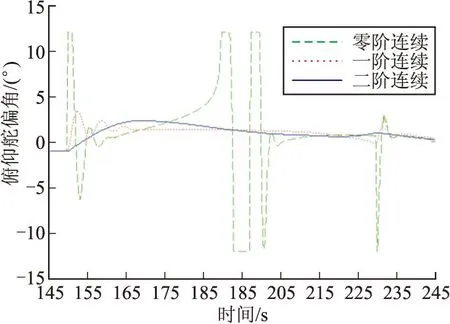
圖13　俯仰舵偏角隨時間變化仿真結果

從圖11~圖14可以明顯看出,在降高段起點(t=150 s)和終點(t=230 s)附近,高度二階導數連續的方案由于保證了垂向加速度平穩過渡,舵偏角和攻角都不會產生振動,高度沖出量也明顯小于其他兩種方案。

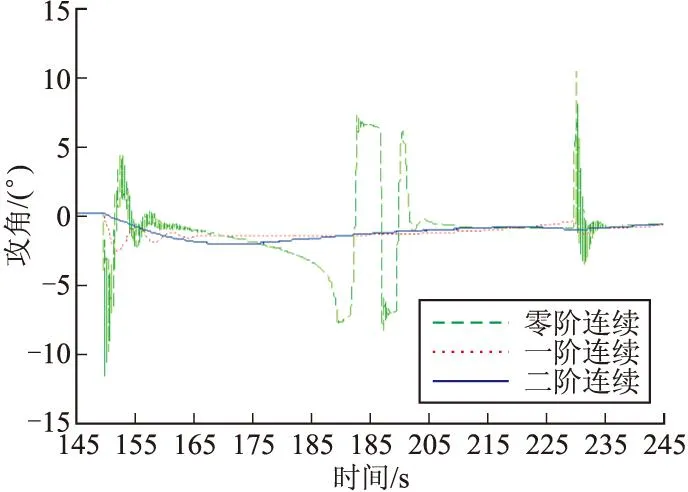
圖14　攻角隨時間變化仿真結果

目前工程中為了取得類似的效果,一般采取增加俯仰阻尼、角速度阻尼[9]或對控制指令進行平滑處理等措施,但這些措施無疑增加了控制系統的復雜度。

由以上分析得出如下結論:在完全相同的控制器作用下,高度導數可導的階數越高,高度沖出量越小,垂向加速度、攻角過渡越平穩,舵的作動也越少。為了使巡飛彈飛行狀態在彈道銜接點能夠平穩過渡,降高方案彈道的設計應保證高度二階導數(即垂向加速度)與前后兩段彈道連續。

5結論

文中通過分析現有降高方案彈道導致機載巡飛彈在彈道銜接點處彈體產生抖動的原因,提出了一種改進的降高方案彈道設計方法,并使用該方法對正弦函數形式的降高彈道進行優化設計,在完全相同的仿真條件下對三種不同階次可導的方案進行數學仿真。仿真結果表明:在不增加控制系統復雜度的情況下,本方法對現有方案改進效果明顯,減小了降高彈道終點的高度沖出量,提高了機載巡飛彈飛行穩定性和生存能力。本設計方法同樣可以用于巡航導彈、無人機等飛行軌跡中存在較大空域降高軌跡的飛行器。

參考文獻:

[1]郭美芳, 彭翠枝. 巡飛彈: 一種巡弋待機的新型彈藥 [J]. 現代軍事, 2006(4): 49-52.

[2]慈旋, 周龍, 邵兵. 基于彈道仿真的空艦導彈降高位置研究 [J]. 大眾科技, 2010(6): 68-69.

[3]王洪強, 邵曉巍, 楊黔龍, 等. 某型滑翔增程靶彈方案彈道設計 [J]. 現代防御技術, 2012, 40(2): 27-31.

[4]陳濤, 丁軍輝. 當前導彈飛行力學研究中的問題分析 [J]. 黑龍江科技信息, 2008(10): 44.

[5]顏仲新, 劉鼎臣. 反艦導彈飛行彈道探討 [J]. 飛航導彈, 2002(2): 33-36.

[6]李一龍, 王光輝, 呂超. 掠海飛行高度對反艦導彈突防能力的影響 [J]. 四川兵工學報, 2014, 35(1): 45-48.

[7]錢杏芳. 導彈飛行力學 [M]. 北京理工大學出版社, 2000: 86-87.

[8]張志涌. 精通MATLAB R2011a [M]. 北京: 北京航空航天大學出版社, 2013: 130-132.

[9]谷良賢, 溫炳恒. 導彈總體設計原理 [M]. 西安: 西北工業大學出版社, 2004: 309-313.

收稿日期:2014-12-16

作者簡介:車曉濤(1990-),男,陜西合陽人,碩士研究生,研究方向:巡飛彈總體技術,制導與控制技術等。

中圖分類號:TJ765.1

文獻標志碼:A

A Project Trajectory with 2nd-derivative Being Continuous of
Large-space Height Descent for Airborne Loitering Munitions

CHE Xiaotao1,WANG Xiao1,HAO Feng1,LI Haicheng1,SUN Huyuan2

(1No.203 Research Institute of China Ordnance Industries, Xi’an 710065, China;

2Frontier Defence Academy of PLA, Xi’an 710108, China)

Abstract:At the beginning and ending points of large-space height descent trajectory, airborne loitering munitions will oscillate severely and the transition time lasts too long. By researching the height-continuous and the velocity-continuous project trajectory, the physical reasons of those phenomena were analyzed. A novel trajectory for height descent with vertical acceleration being continuous was designed based on trajectory optimization. This height descent project trajectory can realize smooth and quick transition between different trajectories without changing the control system, and it also reduces height overshooting of the loitering munitions. An example was given, validating the effect of this trajectory design method, and it will provide reference for trajectory design of airborne loitering munitions and other similar munitions.

Keywords:airborne loitering munitions; large-space height descent; project trajectory; trajectory optimization