多管火箭炮阻尼特性研究*

李　霞,畢世華,傅德彬,王新星,牛青林

(1　北京理工大學宇航學院,北京　100081;2　中國兵器工業導航與控制技術研究所,北京　100089)

多管火箭炮阻尼特性研究*

李霞1,畢世華1,傅德彬1,王新星2,牛青林1

(1北京理工大學宇航學院,北京100081;2中國兵器工業導航與控制技術研究所,北京100089)

摘要:多管火箭炮系統阻尼是系統動態響應的重要參數,對連射時序和射擊間隔有著重要的影響。針對多管火箭炮的典型結構,從理論上分析了影響系統阻尼特性的典型因素,運用多體動力學方法建立的計算模型進行仿真分析,仿真結果與理論分析一致。研究結果表明發射裝置起落架與回轉體間約束副的摩擦效應、起豎油缸阻尼效應、部件的彈性變形對多管火箭發射時的阻尼特性有著決定作用,而金屬結構的材料阻尼特性對發射時的系統阻尼影響較小。

關鍵詞:多管火箭炮;振動響應;阻尼特性;多體動力學

0引言

多管火箭發射時,定向管受到彈管碰撞接觸以及發動機噴出的燃氣射流沖擊等共同作用,使得管口產生顯著的振動響應。火箭彈脫離定向管約束后,振動響應的衰減速率主要由系統阻尼特性決定,進而決定多管火箭炮的連射射序和射擊間隔,因此,對多管火箭發射裝置的阻尼特性進行深入研究是有必要的。

針對多管火箭發射裝置的振動問題,不少學者從振動控制的角度出發,開展了較多研究。例如,徐振欽等[1]針對多管火箭炮采用復合阻尼鋼板連接回轉體與底盤、搖架與發射箱,以實現多管火箭炮減振設計;此外,徐振欽等[2]還利用多管火箭高低機和方向機液壓系統變剛度與阻尼技術實現發射裝置振動控制;陳兵等[3]針對多管火箭炮對回轉和俯仰部分利用變電磁阻尼實現定向器的振動控制。這些研究大多從不同角度出發增加發射裝置的系統阻尼,以達到控制系統振動響應的目的,對影響系統阻尼特性的因素及多阻尼器間阻尼的傳遞關系等尚缺少全面的分析。

文中以多管火箭炮為對象,從起落架與回轉體間約束副的摩擦效應、起豎油缸阻尼效應以及結構的材料阻尼等角度出發,分析發射系統阻尼特性的影響因素,并利用多體動力學方法仿真分析簡化發射裝置的阻尼特性,以進一步明確影響系統阻尼的關鍵因素。

1發射裝置阻尼特性的理論分析

1.1　系統振動響應分析

多管火箭發射過程中,系統的振動響應一般可分為3個階段[2]:1)受定向管約束期間,火箭彈在推力作用下向前運動,火箭彈與定向管碰撞接觸,此時作用在發射裝置上的激勵主要為彈管間碰撞接觸所產生的作用力,是瞬態激勵作用下的強迫振動響應階段;2)火箭彈后定向鈕脫離定向管約束后,作用在發射裝置上的彈管碰撞力為零,這時定向管受發動機噴出的燃氣射流沖擊作用,火箭炮依然處于強迫振動階段;3)火箭彈飛行遠離定向管,燃氣射流沖擊作用完全衰減后,火箭彈對火箭炮的作用力為零,火箭炮整體進入自由衰減階段。

基于對發射系統響應的分析,在不考慮推力偏心、質量偏心及燃氣射流沖擊載荷作用等情況下,火箭彈脫離定向管約束后,外部激勵為零,系統進行自由衰減振動,此時振動響應衰減速率主要由系統阻尼特性決定,系統阻尼增大,則衰減加速。

1.2　阻尼特性分析

2仿真分析模型

2.1　數學模型

基于發射裝置的實際結構及運動情況,將發射裝置簡化為N個組件共同構成的多體系統。

對于多體系統的第i個柔體或剛體,其拉格朗日方程為[6]:

(1)

式中:T為柔體或剛體的動能;λ為拉氏乘子;Qj為廣義力,包括單元彈性變形和外加載荷引起的廣義力。

系統的約束方程:

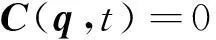
(2)

方程(1)和(2)構成系統的多體動力學方程。

為了驗證理論分析結果并進一步明確發射裝置的阻尼特性,利用ADAMS分別建立多剛體和剛柔耦合動力學模型,并對所建模型進行數值計算分析,其中柔性體的建立是在ANSYS中利用模態綜合法生成模態中性文件,并導入到ADAMS中實現的。

2.2　仿真模型

多管火箭發射裝置結構比較復雜,為研究發射裝置的阻尼特性,在建立動力學模型時,必須對其進行適當的簡化。根據系統各部件間運動關系,將該系統簡化為與回轉體一體固定的發射車、起落架、定向管、前中后3組定向鈕及火箭彈5個部分。結構中的車體大梁長度較長,因此可將其作柔性體處理,起豎油缸及調平油缸柔性連接利用彈簧阻尼器來模擬,其它部分均視為剛體,因此可建立如圖1描述的系統模型。基于圖1的描述,分別建立多剛體動力學模型和以發射車為柔性體的剛柔耦合動力學模型,以此分析柔性體及結構阻尼對系統阻尼特性的影響。定向鈕與定向管間的接觸力主要采用基于Herz碰撞理論的接觸算法[7]獲得,接觸參數與參與接觸的部件的材料屬性有關。參考軟件經驗值及文獻[8-9],表1列出了接觸主要參數值,并且起豎油缸的剛度系數設為20 kN/mm,調平油缸的剛度和阻尼系數分別設為25 kN/mm和50 N·s/mm。文中在不考慮推力偏心、質量偏心和燃氣流作用等情況下,在常推力載荷激勵下,就單發火箭彈發射時定向管管口的垂向位移振動響應進行分析,以基于對數衰減率法[10]獲得的阻尼比來表征系統阻尼特性。

圖1　多管火箭發射裝置模型

剛度系數/(kN/mm)阻尼系數/(N·s/mm)冪指數靜摩擦系數動摩擦系數2.211001.90.30.2

3影響系統阻尼比的因素分析

對多體動力學模型進行仿真,得到對應于不同起豎油缸阻尼系數、回轉體與起落架間約束副摩擦系數和柔性體模態阻尼比的定向管管口垂向位移振蕩曲線。從仿真結果可以看出,約束期內,隨著火箭彈向前移動,定向管管口先下沉至最大下沉量后逐漸回彈,至火箭彈滑離定向管后,外部激勵為零,此后發射裝置進入自由振動響應階段,并且響應幅值在自身阻尼特性作用下最終趨于收斂,但由于發射裝置總重量減小,發射裝置無法再回復到原狀態。

本節利用上述仿真計算模型,結合不同的參數設置分析系統阻尼特性的影響因素。

3.1　起豎油缸阻尼系數對系統阻尼比的影響

圖2描述了在回轉體與起落架間理想轉動副的約束下,起豎油缸阻尼系數從20~200 N·s/mm變化時多剛體模型管口垂向位移振蕩曲線,從圖中可以看出,起豎油缸阻尼系數增大,定向管管口垂向位移幅值(與平衡位置的相對位移的絕對值)減小,響應周期變化小,且隨著時間的增加,幅值下降速度加快,以阻尼系數分別為20 N·s/mm和100 N·s/mm的振蕩曲線中火箭彈離筒后出現的第三個最大正向峰值A3為例分析,阻尼系數增加4倍,幅值減小31.34%。

圖2　不同起豎油缸阻尼下多剛體模型的管口垂向位移曲線

3.2　約束副摩擦系數對系統阻尼比的影響

圖3給出了在起豎油缸阻尼為零的前提下,約束副靜摩擦系數分別為0.1、0.15、0.3、0.5、0.6時相應的多剛體模型管口垂向位移振蕩曲線,此時相對應的動摩擦系數分別為0.05、0.1、0.2、0.3、0.4,易知,靜摩擦系數增大,定向管管口垂向位移幅值減小,且隨著時間的增加,幅值的減小速度加快。同樣的,以約束副靜摩擦系數分別為0.1和0.5時曲線中的峰值A3為例,約束副靜摩擦系數增加4倍,幅值減小66.67%。

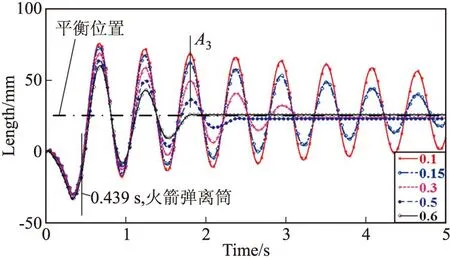
圖3　不同約束副摩擦系數下多剛體模型的管口垂向位移曲線

從圖2、圖3中可以看出,系統響應周期變化較小,這主要是由于系統阻尼比相對于系統固有頻率小得多,自由振動響應周期主要受固有頻率的影響。

由以上分析可知,隨著起豎油缸阻尼系數或起落架與回轉體間約束副靜摩擦系數的增大,則定向管管口垂向位移振蕩衰減加速,系統阻尼比增大,且約束副摩擦阻尼對阻尼比的影響較起豎油缸阻尼大,與理論分析相一致。

3.3　結構柔性變形對系統阻尼比的影響

圖4描述了在起豎油缸阻尼系數為100 N·s/mm和理想約束副的前提下,多剛體模型與剛柔耦合模型的定向管管口垂向位移響應曲線,易知,柔性體的加入使得定向管管口垂向位移幅值增加,以峰值A3為例,與多剛體模型相對比,加入柔性體的模型的定向管管口垂向位移幅值增加57.32%,并且剛柔耦合模型的系統振動響應明顯滯后于多剛體模型,這主要是由柔性體的彈性變形造成的,與文獻[11]結果一致;圖5給出了在不計約束副摩擦阻尼和起豎油缸阻尼時,柔性體模態阻尼比分別為0、0.02、ADAMS軟件缺省值[12]、0.08和0.1時的定向管管口垂向位移響應曲線,易從圖中看出,不同模態阻尼比下的位移響應衰減均較小,且響應周期不變,以峰值A3為例,模態阻尼比增加4倍(0.02~0.1)時,幅值減小2.15%。由于模態阻尼比是物體材料阻尼的一種表征形式[13],故柔性體材料阻尼的變化對系統振動響應幅值和周期影響小,與理論分析相符。

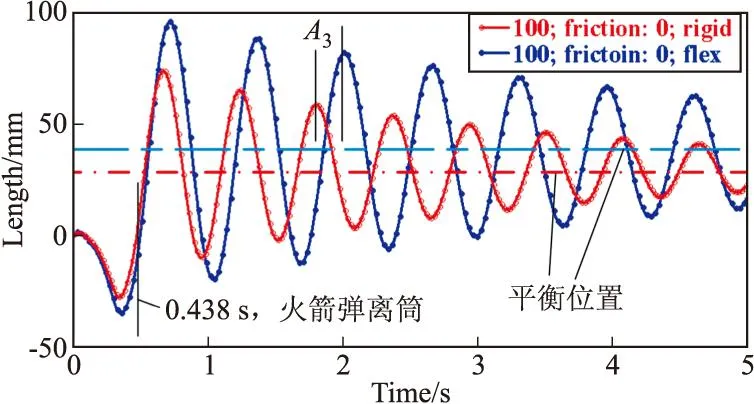
圖4　基于多剛體模型與剛柔耦合模型的管口垂向位移曲線

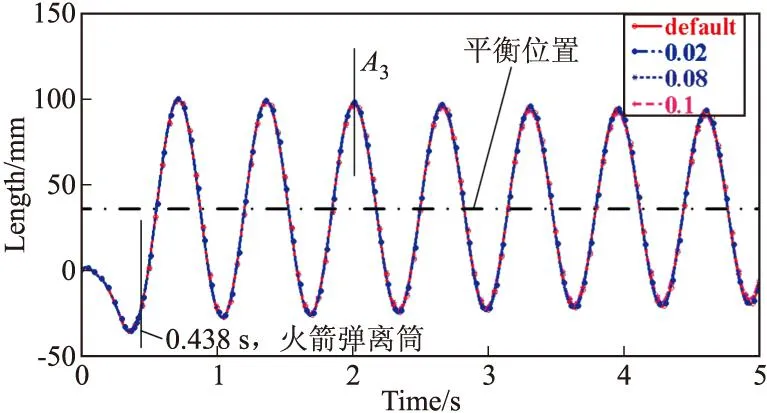
圖5　不同柔性體模態阻尼比下的管口垂向位移曲線

3.4　影響系統阻尼比的典型因素

圖6描述了起豎油缸阻尼系數分別為20 N·s/mm、100 N·s/mm時,約束副靜摩擦系數從0變化至0.6時多剛體模型與剛柔耦合模型的阻尼比值,其中柔性體模態阻尼比設為ADAMS缺省值[12]。從圖中可知,在同一起豎油缸阻尼和約束副摩擦系數條件下,加入柔性體的動力學模型比多剛體模型的阻尼比小,這主要歸因于柔性體的彈性變形。由仿真結果知,起豎油缸阻尼系數為100 N·s/mm,約束副靜摩擦系數為0.15時,剛柔耦合模型的系統阻尼比為0.051,多剛體模型的系統阻尼比為0.087。

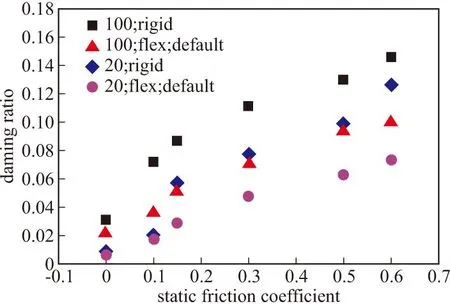
圖6　基于多剛體模型與剛柔耦合模型的阻尼比

起豎油缸阻尼系數/(N·s/mm)總體阻尼比206.57×10-31002.14×10-2相對變化量/%226

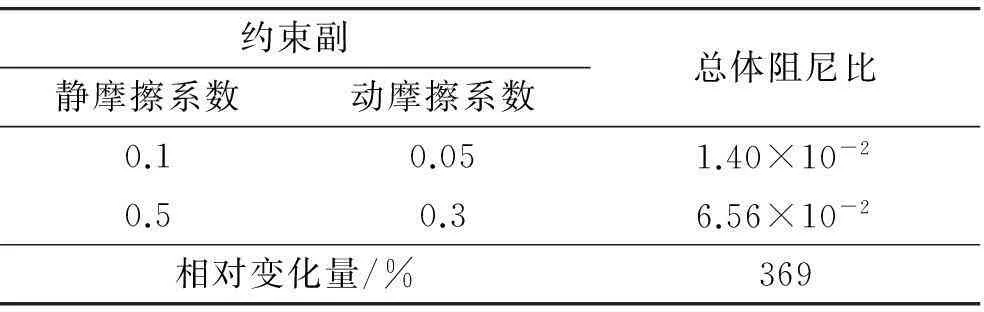
表3　起落架與回轉體間約束副摩擦阻尼的影響

表2、表3分別為對應約束副零摩擦時不同起豎油缸阻尼、起豎油缸零阻尼時起落架與回轉體間約束副摩擦阻尼的剛柔耦合模型的阻尼比,從這兩個表中可以看出,約束副摩擦阻尼為0時,起豎油缸阻尼系數增加4倍,此時剛柔耦合模型的阻尼比增加2.26倍;起豎油缸阻尼為0時,約束副靜摩擦系數增加4倍,剛柔耦合模型的阻尼比增加3.69倍,表明約束副摩擦阻尼對阻尼比的影響較起豎油缸阻尼大。

仿真結果表明,結構的材料阻尼對系統的阻尼特性影響較小,而起豎油缸阻尼、起落架與回轉體間約束副摩擦效應及柔體的彈性變形影響較大,且約束副摩擦阻尼對阻尼比的影響較起豎油缸阻尼大,驗證了理論分析的可靠性,并明確了系統振動響應的影響因素,具有一定的工程意義。

4結論

系統阻尼特性對多管火箭炮的連射射序和射擊間隔的確定有著重要的影響。文中從力學理論出發,分析了多管火箭發射時影響系統阻尼特性的典型因素,并建立了多剛體動力學和剛柔耦合動力學模型進行計算分析,獲得如下結論:

1)發射裝置起落架與回轉體間約束副的摩擦效應、起豎油缸阻尼系數和柔性體的彈性變形對多管火箭發射時的阻尼特性有著決定作用,而金屬結構的材料阻尼特性對發射時的系統阻尼影響較小;

2)起豎油缸阻尼系數或起落架與回轉體間約束副靜摩擦系數增大時,定向管管口擾動衰減加快,系統阻尼比增大,且約束副摩擦阻尼對系統阻尼比的影響較起豎油缸阻尼大;柔性體的加入減緩了定向管管口擾動的衰減速度,其材料阻尼對系統阻尼影響較小。

參考文獻:

[1]徐振欽, 馬大為, 樂貴高, 等. 箱式火箭炮系統阻尼減振仿真分析 [J]. 彈箭與制導學報, 2005, 25(2): 77-79.

[2]徐振欽, 馮勇, 于存貴. 發射裝置沖擊振動的液壓系統變阻尼控制 [J]. 機床與液壓, 2009, 37(10): 106-109.

[3]陳兵, 馬大為, 樂貴高. 多管火箭系統變阻尼振動控制研究 [J]. 彈箭與制導學報, 2006, 26(1): 763-765.

[4]胡海巖. 機械振動基礎 [M]. 北京: 北京航空航天大學出版社, 2005: 7-13.

[5](美)SILVA C W D. 振動阻尼、控制和設計 [M]. 李惠彬, 張曼, 等譯. 北京: 機械工業出版社, 2013: 1-8.

[6]馮勇, 馬大為, 薛暢, 等. 多管火箭炮剛柔耦合多體發射動力學仿真研究 [J]. 兵工學報, 2006, 27(3): 545-548.

[7]徐振欽, 馬大為, 樂貴高. 基于碰撞接觸的彈管多體動力學建模與仿真 [J]. 系統仿真學報, 2007, 19(5): 965-968.

[8]陳余軍, 姜毅. 車載導彈發射過程姿態模擬 [J]. 彈道學報, 2012, 24(1): 102-106.

[9]傅德彬. 數值仿真及其在航天發射技術中的應用 [M]. 北京: 國防工業出版社, 2011: 238-280.

[10]王寶元, 衡剛, 周發明, 等. 炮塔轉動阻尼系數試驗測試技術 [J]. 火炮發射與控制學報, 2013(1): 67-70.

[11]殷增振, 畢世華. 車載導彈多柔體發射動力學仿真研究 [J]. 彈箭與制導學報, 2009, 29(2): 183-185.

[12]李軍, 邢俊文, 覃文潔. ADAMS實例教程 [M]. 北京: 北京理工大學出版社, 2002: 191-194.

[13]梁超鋒, 歐進萍. 結構阻尼與材料阻尼的關系 [J]. 地震工程與工程振動, 2006, 26(1): 49-55.

收稿日期:2014-05-26

作者簡介:李霞(1989-),女,湖南人,碩士研究生,研究方向:發射動力學與振動控制。

中圖分類號:TJ393

文獻標志碼:A

A Study on Damping Characteristics of Multiple Launch Rocket System

LI Xia1,BI Shihua1,FU Debin1,WANG Xinxing2,NIU Qinglin1

(1School of Aerospace Engineering, Beijing Institute of Technology, Beijing 100081, China;

2China Institute of Weapon Industry Navigation and Control Technology, Beijing 100089, China)

Abstract:The damping of multiple launch rocket system (MLRS) is key parameter of dynamic responses, which influences firing orders and firing interval. For typical structure of MLRS, typical factors of its damping characteristics were analyzed theoretically and the numerical models based on multi-body dynamics method were simulated. The simulation results are consistent with theoretical analysis. The results show that friction in the joint between landing gear and rotary body, erecting cylinder damping and the deformation of flexible bodies are decisive factors of the damping characteristics, while material damping of the metal structure has little effect.

Keywords:multiple launch rocket system (MLRS); vibration response; damping characteristics; multi-body dynamics