平均彈道一致性檢驗方法分析及改進*
宋艾平,郭曉剛,王益華,熊 偉
(1 63863部隊,吉林白城 137000; 2 63867部隊, 吉林白城 137000)
平均彈道一致性檢驗方法分析及改進*
宋艾平1,郭曉剛1,王益華2,熊偉1
(163863部隊,吉林白城137000; 263867部隊, 吉林白城137000)
摘要:文中針對利用少量樣本進行檢驗造成平均彈道一致性檢驗判據中正態特性發生變化等問題,利用正態性檢驗、穩健估計等統計學方法,對試驗樣本進行了預先檢驗和數據預處理,重建了檢驗模型,得出了新的檢驗方法,并對改進后的檢驗方法進行了驗證,結果表明該方法具有更好的可靠性和適用性。
關鍵詞:彈道一致性;正態分布;正態性檢驗;M估計
0引言
兵器科學領域對于采用配對t檢驗[1]驗證彈道一致性的方法,普遍對判據合理性、散布和樣本量大小以及系統誤差選取等因素對檢驗結果的影響存在質疑[2-3],在試驗中也曾發現兩彈種未通過彈道一致性檢驗仍能通過射表檢查的案例。文中嘗試通過對原始數據進行分析、統計探尋矛盾存在原因,抽取隨機數比較計算,以期獲得更為科學的檢驗辦法。
1平均彈道一致性檢驗方法分析
1.1 平均彈道一致性檢驗方法
目前,按發交叉射擊時彈道一致性評定采用如下評定標準[4]:
(1)
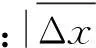
檢測點若滿足下列條件[5],則認為其可作為配對檢驗觀測值。
1)2個不同的滿足正態分布的個體,除了檢驗假設所涉及的系統誤差d外,其他所有方面都相似;
2)2個觀測值之差滿足正態分布。
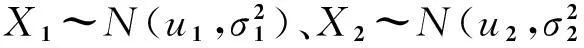
1.2 存在的問題
1)觀測樣本的正態性

表1 各口徑彈藥彈著點坐標正態性統計結果
對各口徑彈著點坐標的正態性檢驗統計結果如表1所示。結果表明平均約10%的數據組不服從正態分布。從正態分布中抽取10 000組隨機數,每組7個樣本,結果4.38%不服從正態分布。
2)觀測樣本之差的正態性
對各口徑彈著點之差的正態性統計結果如表2所示。結果表明平均約10%的數據組不服從正態分布。從標準正態分布中抽取10 000組隨機數,每組7對樣本,配對做差,結果4.57%不服從正態分布。

表2 各口徑彈藥彈著點之差的正態性統計結果
3)對比彈序的選取
在平均彈道一致性試驗中發現,利用原有數據,采用剔除首發和末發彈著點數據,即改變對比彈序的方法進行計算,存在與原檢驗結果不一致的情況。
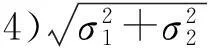
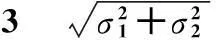
表和σΔ比較的統計結果
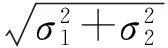
1.3 原因分析
對試驗條件及樣本量進行分析,產生上述現象原因如下:
1)彈藥加工、裝配、裝填、射擊諸元賦予差異以及氣象波動造成彈著點存在差異,在數據處理過程中不作任何修正即納入一致性判據,使抽樣樣本偏離了正態總體;
2)樣本量小,極少數偏離樣本數學期望的樣本作為典型樣本數據混入數據處理,致使樣本及樣本差值均不能真實反映樣本總體及兩個總體差所在總體的樣本特征。
上述原因造成了彈著點及其差值不滿足正態分布、減差時彈序對結果有影響、計算獲得的方差不符合正態分布特性等情況。
2平均彈道一致性檢驗方法的改進
2.1 平均彈道一致性檢驗模型
根據上述論述,為保證抽樣樣本滿足配對t檢驗的檢驗假設,有必要對抽樣樣本進行以下處理:
1)對抽樣樣本是否正態進行甄別。
2)對非正態樣本,進行樣本處理。
非正態樣本處理可以通過數學方法弱化異常樣本對樣本總體的影響或者剔除異常樣本兩種方法來實現。試驗中,除少量離群值外,難以將異常樣本與樣本其他數據區分開,且剔除異常樣本可能造成抽樣樣本特征的改變,獲得錯誤的估計參數,增加研制方或鑒定方的風險。穩健估計采用對樣本數據加權的方法,能在拒絕和接受1個觀測值之間起到平滑的作用,既保留了觀測值的樣本特征,又降低了異常樣本特征對參數計算的影響,使其更加接近實際應服從的分布類型。其中M估計[6]用于解決異常樣本呈非正態性分布問題具有較好的抵抗異常樣本的能力,更適于該類處理。
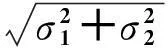
改進后平均彈道一致性檢驗模型如圖1所示。

圖1 平均彈道一致性檢驗模型
2.2 正態性檢驗
正態性檢驗的方法主要有χ2擬合優度檢驗、柯爾莫戈洛夫檢驗、W檢驗、D檢驗、偏度檢驗、峰度檢驗和偏度、峰度聯合檢驗。前兩種方法為萬能檢驗方法,對正態性檢驗不具有特效;W檢驗適用于樣本容量為3≤n≤50的情況;D檢驗適用于樣本容量為50≤n≤1 000的情況。根據Shapiro和Wilk對以上正態性檢驗的研究,W檢驗法更適于無方向上偏離先驗信息且樣本容量較小的彈道一致性試驗,即:
假設H0:總體服從正態分布,H1:總體不服從正態分布。
將n個樣本測量值按由小到大次序排列為X(1)≤X(2)≤…≤X(n),則有統計量[7]:
(2)
式中:ai(W)為W檢驗的檢驗系數;[n/2]為對n/2取整,其中n為樣本容量。
給定置信水平α,查表獲得ai(W)及統計量W的分位數Wα,計算W,若W M估計的基本原理是在一般極大似然估計的基礎上,將異常樣本歸于隨機模型,通過定義某個優化的影響函數來取代最小二乘函數,并根據逐次迭代平差的結果不斷的改變觀測值的權或方差,最終使異常樣本的權趨于0,或方差趨于無窮大,以減小奇異點的影響,具有良好的統計特性和廣泛的適用性。對比常用的穩健函數,Huber函數分別基于最小最大偏差準則和最大漸進方差準則,計算量最少,對正態分布數據具有95%的估計效率,同時能有效抵抗奇異點干擾,對于均值和方差的估計具有較好效果[5-6,8]。文中利用Huber位置、刻度函數組成泛函方程組(3)對樣本均值和方差進行穩健估計。t、s分別為樣本均值和方差的M估計值,取自變量為(Xi-t)/s,c=1.345,β=0.710 1。 (3) (4) (5) (6) (7) 3試驗應用 某型彈藥2 000m立靶試驗中,發交叉射擊2組,每組研制彈、對比彈各10發。按式(1)檢驗發現,高低坐標不滿足一致性要求。對研制彈進行通用射表檢查發現二者通用射表與檢驗結果相矛盾。 分別按現行檢驗方法和改進方法進行計算,結果見表4。分析計算結果,可以獲得以下結論: 1)經W檢驗僅62.5%符合正態分布,利用傳統參數計算方法不能獲得準確的總體分布參數; 3)改進后方法獲得的結果與通用射表檢查結果一致。 上述檢驗結果表明,在樣本正態分布比例較小時現行檢驗方法與通用射表檢查結果存在差異,按新模型處理后,更能反映彈著點樣本特征,進而獲得了與射表檢查一致的檢驗結果。 表4 某型彈藥平均彈道一致性檢驗結果 4結論 文中結合現行平均彈道一致性檢驗實際應用及隨機數抽樣計算情況,對配對t檢驗理論進行深入研究,發現該理論在試驗客觀條件及小樣本的影響下出現樣本、對比樣本之差不滿足正態分布或正態特性等問題,據此提出了用樣本正態性檢驗、M估計、摒棄成對作差的樣本預處理方法,建立了新的檢驗模型,獲得了新的檢驗方法,驗證試驗證明改進后方法與通用射表檢查結論一致,具有更高的可靠性和適用性。 參考文獻: [1]閆章更. 試驗數據的統計分析 [M]. 北京: 國防工業出版社, 2001: 97-118. [2]董滿才, 劉云南. 彈道一致性檢驗若干問題的辨析 [J]. 彈箭與制導學報, 2011,31(4): 152-154. [3]王聲生. 彈道一致性試驗判據的分析與建議 [J]. 四川兵工學報, 2011(10): 64-66. [4]GJB4225-2001 榴彈定型試驗規程 [S]. 2001. [5]張領科, 王中原, 王楓. 彈道一致性檢驗準則應用中的問題分析和建議 [J]. 彈道學報, 2005, 17(4): 17-21. [6]王家幫, 脫立文, 吳友平. M估計的權函數選取及其抗差性比較 [J]. 山西建筑, 2008, 34(13): 351-352. [7]梁小筠. 正態性檢驗 [M]. 北京: 中國統計出版社, 1997. [8]王聲生. 基于穩健估計的彈道一致性試驗方法 [J]. 艦船電子工程, 2011, 31(11): 132-135. 版 權 聲 明 凡稿件被本刊錄用,即視為作者同意將該論文的復制權、發行權、信息網絡傳播權、翻譯權、匯編權等權利在全世界范圍內轉讓給本刊。本刊已許可中文科技期刊數據庫(維普)、萬方數據數字化期刊群和中國知網(中國學術期刊(光盤版)電子雜志社)在其各自的系列數據庫產品中以數字化方式復制、匯編、發行及在信息網絡傳播本刊全文。作者著作權使用費和稿酬一并支付(即包括印刷版、光盤版和網絡版各種使用方式的報酬)。如作者對本聲明持有異議,請在投稿時說明。 本刊編輯部 收稿日期:2014-11-08 作者簡介:宋艾平(1979-),女,吉林白城人,碩士,研究方向:彈藥鑒定。 中圖分類號:TJ4 文獻標志碼:A The Analysis and Improvement on Test Method of the SONG Aiping,GUO Xiaogang,WANG Yihua,XIONG Wei (1No.63863 Unit, Jilin Baicheng 137000, China; 2No.63867 Unit, Jinlin Baicheng 137000, China) Abstract:Aiming at the question of the test criterion of average trajectory consistency, it thinks out that small sample is the reason of normal characteristic’s charge. The pretest and data pretreatment is give with normality test and robust estimation for test sample. It rebuilds a test model and obtains a new test method. According to the testing result, the method has high applicability and reliability. Keywords:the average trajectory consistency; normal distribution; normality test; M-estimation2.3 M估計

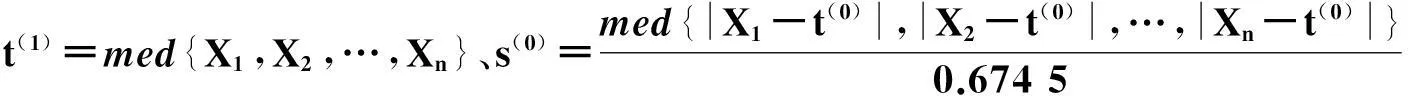

Average Trajectory Consistency

