用LES和無限元耦合方法預報潛艇流噪聲

王 超，鄭小龍，張立新，魏勝任

（哈爾濱工程大學 船舶工程學院,哈爾濱 150001）

用LES和無限元耦合方法預報潛艇流噪聲

王 超，鄭小龍，張立新，魏勝任

（哈爾濱工程大學 船舶工程學院,哈爾濱 150001）

為了系統地研究潛艇流噪聲的特點，采用大渦模擬（LES）與聲學無限元方法耦合，對潛艇進行頻域噪聲數值預報。在潛艇水動力性能及壓力分布的計算后，再與試驗結果對比分析，驗證了水動力計算方案的準確性。在此基礎上，結合聲學無限元方法，對潛艇流噪聲進行數值模擬，并對特征點進行頻域分析。經噪聲分布云圖和遠場特征點頻譜曲線的詳細分析后，可發現隨著頻率增加，輻射區間均會增多，而相同頻率下四極子噪聲輻射區間要多于偶極子。相比于面聲源，體聲源在總聲級中的貢獻度較小，可以忽略不計。由于計算的特征點總聲壓級與文獻所提供結果吻合，驗證了所采用噪聲預報方法的準確性。

聲學；潛艇；大渦模擬；無限元

潛艇水下輻射噪聲可以分為三類，即機械振動噪聲、水動力噪聲和螺旋槳噪聲。其中，水動力噪聲是潛艇在航行過程中潛艇表面和水流邊界面之間相對運動而引起的隨機噪聲、空化噪聲等[1]。在低速航行中，潛艇水動力噪聲在潛艇噪聲中的比重很小，但隨著航速提高，潛艇的水動力噪聲也將大幅增加，嚴重制約著潛艇的性能。目前對于潛艇水動力噪聲的研究主要通過試驗測量和數值模擬來完成。Skudrzyk E J[2]利用不同尺寸的水聽器對回轉體進行噪聲測量，分析了不同尺寸水聽器對測量結果的影響，并在回轉體表面包裹不同粗糙程度的材料，分析其對結果的影響。畢毅[3]通過自航模拖曳試驗實現潛艇流噪聲測量工作，利用時域信號分析方法，獲得潛艇流噪聲的時域信號。盧云濤[4]采用FLUENT軟件對潛艇模型加載不同附體的流噪聲性能進行了數值模擬，并分析了不同附體對噪聲的影響。曾文德[5]運用計算流體力學（CFD）和邊界元（BEM）相結合的方法，預報全附體潛艇流噪聲，分析了不同頻率下聲指向性的變化規律。計算所得結果與一般聲學規律較為吻合。楊瓊方[6]采用大渦模擬（LES）與聲學邊界元（BEM）相結合的方法，在頻域內預報了流噪聲空間分布、測點譜源級曲線和聲指向性，計算結果表明，流噪聲蝶形指向性對應的輻射瓣狀區間數隨著頻率增加而增加，且正橫方向的聲壓要強于艏艉方向。

本文在采用大渦模擬對潛艇流場進行準確預報的基礎上，結合無限元方法對潛艇噪聲進行數值仿真。系統地比較分析了潛艇部分截面上的壓力分布以及其水平面和中縱剖面上的面聲源和體聲源的聲壓分布，并對特征點處的聲壓譜級與相關文獻進行了驗證分析。

1 流－聲耦合方法理論

1.1 大渦模擬SGS模型

SGS模型在LES方法中占有十分重要的地位，本文應用Smagorinsky-Lilly模型[7-8]來模擬亞格子應力

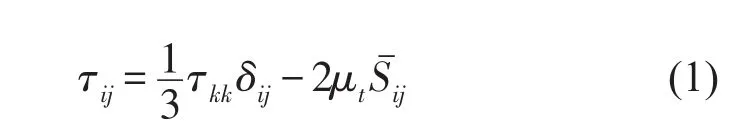
式中μt是亞格子尺度的湍動黏度，在文獻[9]中推薦用下式計算

其中

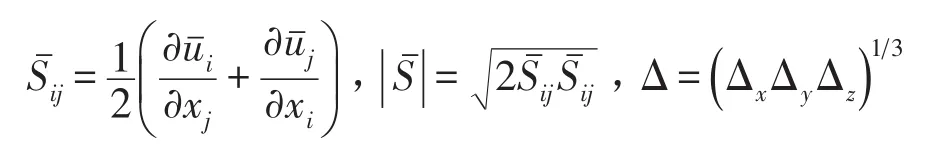
式中Δi代表沿i軸方向的網格尺寸，CS是Smagorinsky常數，對于本文中的研究，沿用Fluent軟件中的默認值，即CS取0.1。

1.2 Lighthill聲學類比理論

Lighthill考慮的模型為：在無限大的均勻、靜態聲介質中包含一個有限的湍流運動區域V。因此，與流動有關的聲源都集中在該區域內。在區域V外，遠離湍流區域的流體中密度的波動和聲波相似。因此，在整理連續方程和動量方程后，可簡化得到遠離湍流區域流體中的勻質聲學波動方程

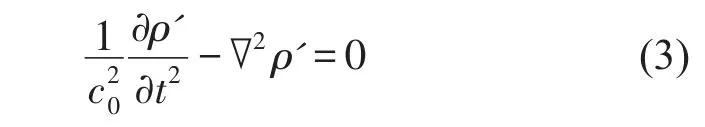
Lighthill聲類比理論是從流體力學基本方程納維-斯托克斯（Navier-Stokes）方程導出的

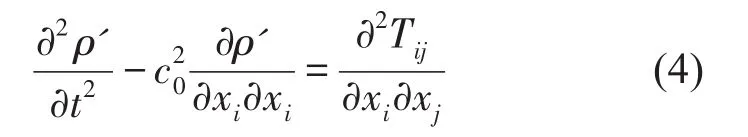
式中c0是等熵條件下的聲速值；ρ'=ρ-ρ0為有聲擾動時的密度分量，ρ與ρ0分別是擾動與未擾動時的流體密度；Tij是Lighthill應力張量[10]。

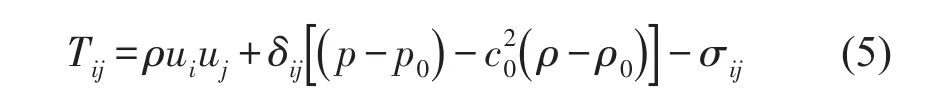
其中σij表示雷諾應力張量的黏性部分。

對于低速等熵流動，黏性應力張量σij對Lighthill應力張量Tij的貢獻遠小于雷諾應力項ρuiuj，可以忽略不計，同時可以得到

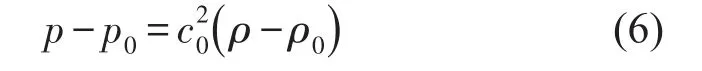
因此，可得到Lighthill應力張量的近似式Tij=ρuiuj。

1.3 ACTRAN聲學原理

ACTRAN基于Lighthill方法，并結合Curle’s理

論[11]：

1）Curle’s方程的體積分作為有限元區域的體源；

2）Curle’s方程的面積分作為邊界條件；

3）自由場的格林函數作為其他的邊界條件。

對(6)式在W邊界上積分，并乘以測試函數δρ，并應用分布積分產生弱變分形式，在面積分上應用應力張量，可得到下式

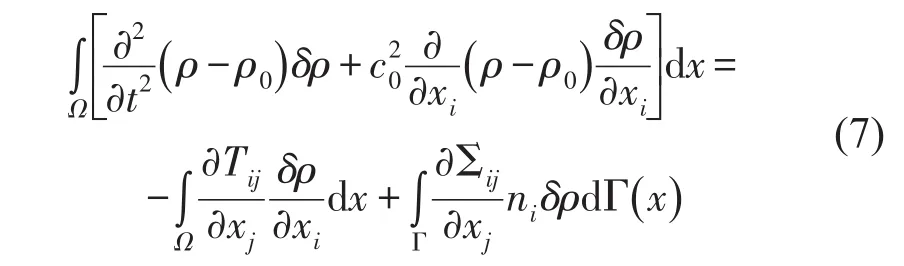
方程右邊第一項為體源，第二項為面源，其中

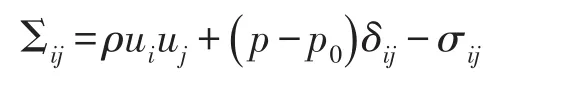
1.4 潛艇噪聲模擬基本流程

ACTRAN軟件處理流致噪聲問題時，CFD計算與聲學計算是解耦的，即首先進行CFD仿真，提取出湍流信息，然后再利用Lighthill聲類比方法分析聲場，對聲場分布及聲傳播進行計算。對于聲學分析中，只要滿足每波長6網格的規則即可，使用積分法將流場信息加載到聲學網格上。因此，不需要對聲源區的網格做特別的優化。

2 計算前處理

2.1 幾何模型建立和計算域的劃分

文章研究潛艇為SUBOFF，其具有比較詳細的流場數據[12]，是美國專門為驗證潛艇水動力數值計算而設計的，成為很多國內外學者工程研究和驗證的對象。

全附體SUBOFF潛艇長4.356 m，艇身最大直徑為0.508 m，平行中體為2.229 m，指揮臺長0.368 m。上部有一外凸的頂蓋，艉翼的翼型后緣位于距艇艏4.007 m處，4個艉翼剖面為NACA 0020翼型，對稱布置。螺旋槳盤面距艇首4.26 m。在建模過程中使用的是直角坐標系O-XYZ，X軸方向代表來流方向，流場計算域來流方向艇首取1倍艇長，艇尾取2倍艇長，徑向取10倍艇身最大直徑，如圖1所示。

圖1 潛艇流場計算域

2.2 網格劃分及參數設定

網格劃分是CFD模擬過程中比較耗時的環節，也是直接影響模擬精度和效率的因素之一。本文在劃分網格時采用全結構化網格。

網格質量直接決定著計算結果的收斂性、效率和精度。考慮到模型的對稱性，只需創建潛艇一側網格，并沿對稱面將其鏡像以完成網格創建工作。劃分網格時，流域整體采用C型網格，并在潛艇表面向外開設O網，如圖2所示。此種方式可在減小邊界層厚度的同時，不使全局網格數目過多，第一層網格厚度取0.000 3，Y+控制在0～40以滿足計算精度要求，整個流域的網格總數為238.1萬。

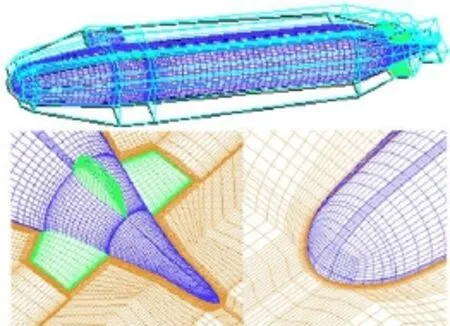
圖2 潛艇結構化網格

3 大渦模擬數值計算

邊界條件采用速度入口和壓力出口，遠場壁面取symmetry邊界條件以消除邊界面帶來的影響，給定來流速度為

在應用Fluent軟件進行流場計算時，首先采用RNGk-ε湍流模型進行定常運算，待獲得穩定流場后，改用LES方法進行非定常運算。計算時采用有限體積法進行離散，擴散相采用中心差分格式，壓力速度耦合采用SIMPLEC算法，連續性曲線小于10-7時認為計算收斂，時間步長取0.000 25 s。

將計算結果與試驗值和經驗值[13，14]進行對比，如表1所示。總阻力計算值比試驗值略大，誤差為1.076%，而摩擦阻力計算值誤差稍大，達到3.376%，總體來說，計算結果顯示了本文計算方法的可行性。

表1 潛艇阻力計算值與試驗值和經驗值比較

分析潛艇表面壓力分布，提取潛艇沿中縱剖面上半緣線上和水線方向指揮臺圍殼截面的壓力分布如圖3和圖4所示，將其與試驗值進行對比，可以看出計算結果與試驗值吻合較好，進一步驗證了本文計算方法的合理性和準確性。

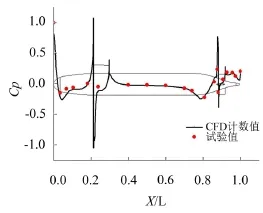
圖3 潛艇縱中剖面脊線壓力系數分布

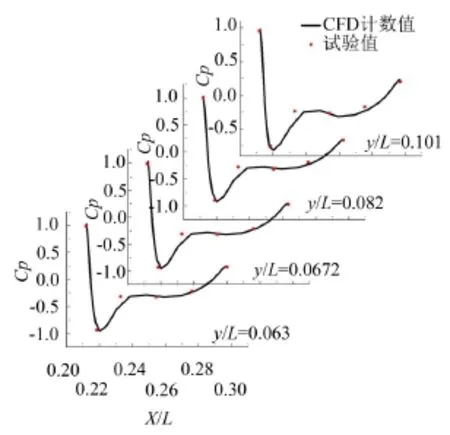
圖4 指揮臺截面壓力系數分布

由圖4可以看出，對于潛艇艏部、指揮臺和艉翼前部，由于速度很小幾乎為零，故該處存在局部高壓區，流體流過指揮臺和艉翼前部后，由于機翼形狀和流體方向的共同作用，流速增加，從而使得壓力迅速減小，觀察兩處峰值大小，可以看出，指揮臺對流場的影響要比艉翼的影響大。同時由圖5中潛艇艇體表面壓力分布可以預測，艏部、指揮臺和艉翼三處對噪聲貢獻相對較大。

圖5 艇體表面壓力等值線圖

4 潛艇噪聲性能預報

4.1 聲學模型的創建和網格劃分

聲學網格包括聲源區和聲傳播區，Actran將聲源分為面聲源和體聲源，面聲源是潛艇面網格，體聲源則是聲源區的體網格，分別對應偶極子聲源和四極子聲源。

與流場大渦模擬相比，聲場計算對網格質量的要求要低的多，考慮到計算精度及計算時間問題，聲學網格尺寸只要滿足每波長至少6個網格節點即可。利用ICEM創建非結構聲學網格，圖6是潛艇表面網格，指揮臺和艉翼處進行了局部加密，以更準確地表征幾何形狀。

圖6 潛艇表面聲學網格

圖7是整個計算域的聲學網格，其中圖示中心為聲源區，取自CFD計算區域，略小于CFD計算區域，以消除邊界假噪聲影響，以外的區域為聲傳播區。CFD節點和聲學網格節點之間通過保守整合法（Conservative integration）進行信息傳遞以保證計算精度。

圖7 聲學計算域非結構網格

4.2 潛艇聲壓云圖分析

截取通過潛艇軸線的水平面，計算得到由面聲源引起的該截面聲壓云圖如圖8所示。

由圖8可知，在低頻段，潛艇附體對聲壓云圖影響較大，這與前文流場計算時的預測相符。潛艇附近聲壓云圖呈現出分別以艏部指揮臺和艉翼為中心的點聲源特性，在其附近，存在局部高聲壓區，隨與潛艇距離增加，潛艇整體呈現出點聲源特性，聲壓等值線中心即為潛艇中心位置，無明顯聲指向性。隨頻率增加，艏艉位置的點聲源特性增加，影響范圍增大，艏艉方向聲壓級較大，艇身中間及兩側處，兩點聲源相互疊加，聲壓相對較小，體現在聲壓等值線上，聲壓等值線在59.85 Hz時的基礎上，在艇身中間附近向內凹陷。

同時，由圖8聲壓云圖綜合對比可以看出，隨頻率增加，“蝶形”指向性越發顯著，同時表現出的瓣狀輻射區間數也相應增多，波峰也更加尖銳，與文獻[15]中描述的一致。同時觀察各頻率下的聲壓云圖可以發現，由于水平截面不通過指揮臺，在低頻段，指揮臺和艉翼附近存在局部高聲壓區，而在高頻段，艉翼附近的高聲壓區則凸顯出來，說明潛艇附體對其附近聲壓影響較大。

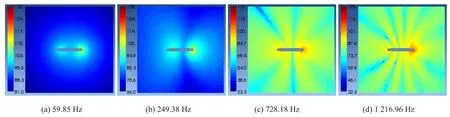
圖8 面聲源聲壓分布云圖（水平面）

截取通過潛艇軸線的縱剖面，計算得到由面聲源引起的該截面聲壓云圖如圖9所示。

由圖8和圖9比較可知，整體規律縱剖面與水平面聲壓云圖相同，隨頻率增加，“蝶形”指向性越發顯著，同時表現出的瓣狀輻射區間數也相應增多，指揮臺和艉翼周圍存在局部高聲壓區，并向外輻射衰減。對比同頻率下兩截面的聲壓云圖，縱剖面中，由于指揮臺影響，聲壓云圖不再對稱。

由體聲源引起的四極子噪聲聲壓云圖如圖10所示，四極子噪聲的聲壓云圖同樣呈蝶形分布，不同的是，在低頻段即顯現出4個輻射區間，在潛艇近場，由于受潛艇艇身影響，湍流雷諾應力較大，使得該處存在高聲壓區。與偶極子噪聲一樣，四極子噪聲聲壓云圖同樣是隨頻率增加而輻射區間增多。然而對比同頻率下的偶極子噪聲和四極子噪聲，四極子噪聲輻射區間要多于偶極子。

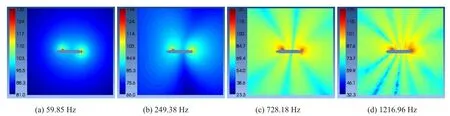
圖9 面聲源聲壓分布云圖（中縱剖面）

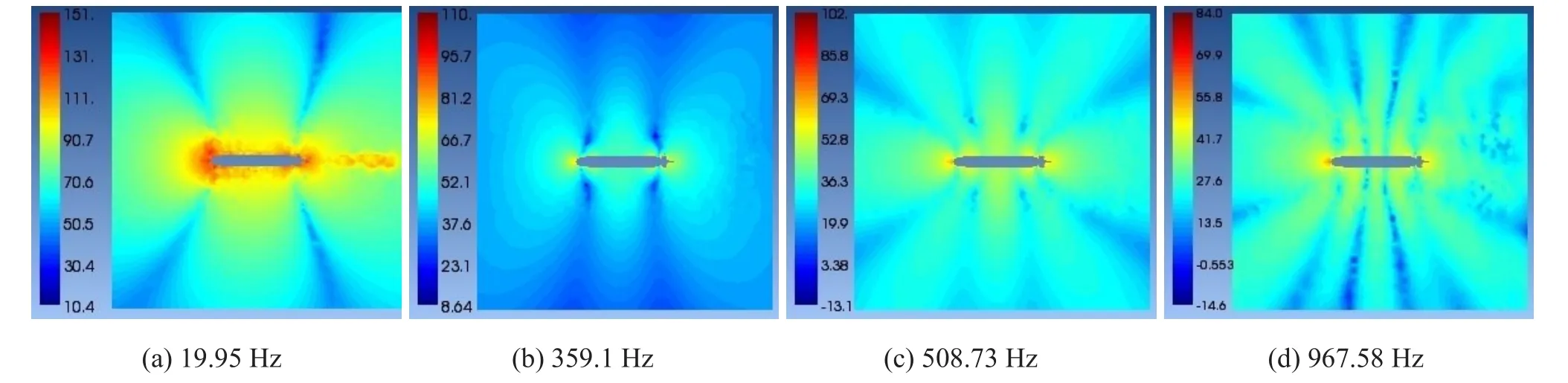
圖10 體聲源聲壓分布云圖（水平面）

4.3 特征點頻域分析

參照文獻[5]的相應設置，取特征點（2.178，－2，0），即艇體正下方2 m處，該點的面聲源和體聲源產生噪聲的頻譜曲線如圖11所示：

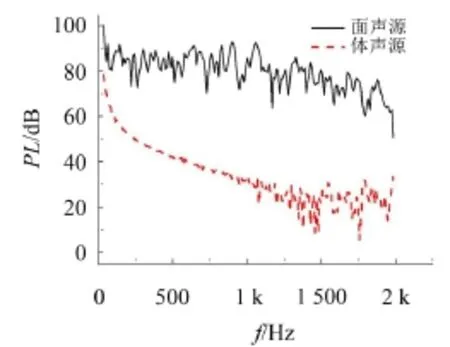
圖11 特征點的聲壓頻譜曲線

觀察頻譜曲線，由面聲源產生的偶極子噪聲在頻域內波動明顯，且整體趨勢隨頻率增加比較穩定，在1 500 Hz之后呈下降趨勢，但趨勢不明顯。由體聲源產生的四極子噪聲在頻域內0～1 000 Hz區間波動很小，呈下降趨勢，在1 000 Hz～2 000 Hz之間，隨頻率變化波動明顯。對比面聲源和體聲源噪聲，可以看出，體聲源噪聲要小很多，均在20 dB以上，可以忽略不計。四極子噪聲也稱為湍流噪聲，它是由于湍流邊界層，艉跡區的湍流脈動，分離流動等流體內部的壓力脈動產生的，由于潛艇在水下航行時，近場區域即艇身附近湍流雷諾應力較大，使得該處存在高聲壓區，而遠場區域馬赫數較低，故產生的四極子噪聲也很小，這也是很多學者在計算潛艇流噪聲時采用邊界元方法的原因[4-6]。

總聲壓級計算公式為

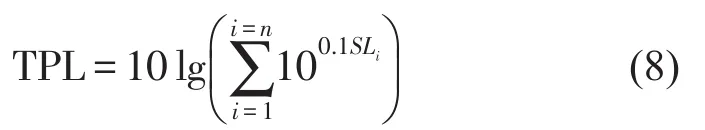
其中SLi是第i個中心頻率點處聲壓級。

計算得到的面聲源噪聲、體聲源噪聲和總噪聲分別是108.385 dB、81.207 dB、108.42 dB，可以看出面聲源噪聲和總噪聲大小相近，符合前文分析得出的結論，即四極子噪聲可以忽略不計。文獻[5]利用計算流體力學（CFD）和邊界元（BEM）相結合的方法算得特征點噪聲大小為108.5 dB，與本文計算結果非常接近，此亦證明了本文計算方法的準確性。

5 結語

本文采用流—聲耦合方法對潛艇流噪聲進行了分析，得出以下結論：

(1)由潛艇阻力和表面壓力分布的計算結果和試驗值十分吻合，驗證了本文所提的LES模型結合全結構化網格技術的計算方案具有較好的結果。同時，通過潛艇艇體表面壓力分布可以預測，艏部、指揮臺和艉翼三處對噪聲貢獻相對較大；

(2)由水平面上面聲源產生的偶極子噪聲分布云圖得知，在低頻段，潛艇附體對聲壓云圖影響較大，呈現出分別以艏部指揮臺和艉翼為中心的點聲源特性，隨與潛艇距離增加，潛艇整體呈現出點聲源特性，聲壓等值線中心即為潛艇中心位置，無明顯聲指向性。隨著頻率的增高，瓣狀輻射區間逐漸出現并增多，“蝶形”指向性也越發顯著；

(3)中縱剖面上產生的偶極子噪聲分布，在整體規律上與水平面上的偶極子噪聲分布基本一致，主要的不同在于由于指揮臺存在于縱剖面中，使聲壓云圖不再對稱；

(4)由水平面上偶極子和四極子噪聲分布云圖比較得知，隨著頻率增加，輻射區間均會增多，而相同頻率下四極子噪聲輻射區間要多于偶極子；

(5)由遠場特征點的頻譜曲線的觀察以及面聲源噪聲、體聲源噪聲和總噪聲的計算結果比較可知，體聲源在潛艇總聲級中的貢獻度較小，可以忽略不計。

[1]王之程，陳宗岐.艦船噪聲測量與分析[M].北京：國防工業出版社，2004.

[2]Skudrzyk E J,Haddle G P.Noise production in a turbulent boundary layer by smooth and rough surfaces[J],J.A.S. A,1960,32(1):19-34.

[3]畢毅，高霄鵬，王波，等.潛艇水動力噪聲的自航模試驗技術研究[J].海軍工程大學學報，2007，05：40-43+55.

[4]盧云濤.全附體潛艇的流場和流噪聲的數值研究[D].上海：上海交通大學，2008.

[5]曾文德，王永生，楊瓊方.全附體潛艇流噪聲數值計算[J].兵工學報，2010，09：1204-1208.

[6]楊瓊方，王永生，張明敏.潛艇渦量場和流噪聲等效聲中心的數值預報[J].華中科技大學學報（自然科學版），2012，05：64-70.

[7]Kobayashi T.Large eddy simulation for engineering applications[J].Fluid Dynamics Research,2006,38:84-107.

[8]Holm D D,Geurts B.Commentator errors in large-eddy simulation[J].Journal of Physics A:Mathematical and General,2006,39:2213-2229．

[9]F Felten,Y Fautrelle,Y Du Terrail,et al.Numerical modelling of electromagnetically-driven turbulent flows using LES methods[J].Applied Mathematical Modelling,28 (1):15-27,2004.

[10]Escobar M.Finite element simulation of flow-induced noise using Lighthill's acoustic analogy[J].Germany: University Erlangen Nurnberg,2007.

[11]Curle N.The influence of solid boundaries upon aerodynamic sound[C].Proc Royal Soc London,Ser A,1955, 231(1187):505-514.

[12]Nancy C Groves,Thomas T Huang,Ming S Chang.Geometric characteristics of DARPA SUBOFF Models[J].David Taylor Research Center,1989.

[13]Liu Hall Lieh,Thomas T Huang.Summary of DARPA suboff experimental program data[R].US:Naval Surface Warfare Center,Carderock Division(NSWCCD),1999.

[14]Bull P.The validation of CFD predictions of nominal wake for the SUBOFF fully appended geometry[A].Proceedings of 21stSymposium on Naval Hydrodynamics [C].Norway,1996,1061-1076.

[15]Urick R I.Principle of underwater noise[M].New York: Mc Graw-Hill,1981:310-313.

Prediction of Submarine Noise Based on LES and Infinite Element Method

WANG Chao,ZHENG Xiao-long,ZHANG Li-xin,WEI Sheng-ren
(College of Shipbuilding Engineering,Harbin Engineering University,Harbin 150001,China)

In order to study the noise property of submarines systematically,a method combining the Large Eddy Simulation(LES)with the infinite element method was used to predict the frequency domain noise of the submarine.Hydrodynamic performance and pressure distribution of the submarine were calculated and compared with the experimental data. The results show that the numerical results agree well with the experimental data,which verifies the accuracy of the numerical method.On this basis,the acoustics infinite element method was employed to simulate the submarine flow noise,and analyze the noise at some special points in frequency domain.Analysis of noise distribution and frequency spectrum curves shows that the number of noise radiation regions of dipoles and quadratic poles increases gradually as the frequency increasing.And the radiation regions of the quadratic pole are more than that of the dipole at the same frequency.In comparison with surface sound source,the body acoustic source has small contribution to the overall acoustic level and can be neglected.

acoustics;submarine;large eddy simulation(LES);infinite element method

TB132；U661.31+3

：A

：10.3969/j.issn.1006-1335.2015.01.01

1006-1355(2015)01-0001-06

2014－07－21

國家自然科學基金項目(51309061)；中央高校基本科研業務費專項資金資助(HEUCFR1102)

王超(1982－)，男，講師，博士后，主要從事船舶推進與節能技術研究。E-mail:wangchao0104@hrbeu.edu.cn