基于區(qū)間數(shù)回歸模型的未決賠款準(zhǔn)備金評(píng)估

馮衛(wèi)澤，王達(dá)布希拉圖

(廣州大學(xué)a.數(shù)學(xué)與信息科學(xué)學(xué)院;b.經(jīng)濟(jì)與統(tǒng)計(jì)學(xué)院;c.嶺南統(tǒng)計(jì)研究中心，廣東廣州 510006)

眾所周知，在非壽險(xiǎn)中未決賠款準(zhǔn)備金是針對(duì)案發(fā)已記錄的但還未完全理賠的保險(xiǎn)風(fēng)險(xiǎn)所預(yù)留的準(zhǔn)備金.由于缺乏類似壽險(xiǎn)生命表的完整的保險(xiǎn)標(biāo)的損失分布表，導(dǎo)致未決賠款準(zhǔn)備金評(píng)估遠(yuǎn)比壽險(xiǎn)中的準(zhǔn)備金計(jì)算復(fù)雜.目前，人們針對(duì)未決賠款準(zhǔn)備金的估算提出了鏈梯法、案均賠款法、準(zhǔn)備金進(jìn)展法、B－F法等，其大致可分為確定性方法和隨機(jī)性方法.前者估算的結(jié)果是一確定的數(shù)，后者估計(jì)出來的未來未決賠款準(zhǔn)備金不是一個(gè)準(zhǔn)確值，而是一個(gè)變量.隨機(jī)的方法相對(duì)于確定性的方法具有明顯的優(yōu)點(diǎn)，例如，隨機(jī)的方法可對(duì)假設(shè)的模型進(jìn)行診斷，并可給出估計(jì)值的置信區(qū)間.KREMER［1］提出對(duì)數(shù)正態(tài)模型，結(jié)合了對(duì)數(shù)正態(tài)分布理論估計(jì)未決賠款準(zhǔn)備金.MACK［2］對(duì)KREMER的模型進(jìn)行部分改進(jìn)，將賠款額看做一個(gè)服從伽馬分布的隨機(jī)變量，給出未決賠款準(zhǔn)備金的伽馬模型.SHERMAN［3］給出指數(shù)型平滑發(fā)展因子模型.RENSHAW等［4］結(jié)合廣義線性模型，運(yùn)用準(zhǔn)極大似然估計(jì)方法進(jìn)行參數(shù)估計(jì).這種方法有助于處理賠款增量出現(xiàn)負(fù)值的問題.孟生旺［5］在假設(shè)增量賠款服從指數(shù)分布族的條件下，應(yīng)用廣義線性模型評(píng)估未決賠款準(zhǔn)備金.盧志義等［6］分析利率厘定和準(zhǔn)備金估計(jì)中廣義線性模型的建模方法，指出數(shù)據(jù)缺失和數(shù)據(jù)質(zhì)量較低是導(dǎo)致傳統(tǒng)模型估計(jì)結(jié)果欠佳的原因.陳迪紅等［7］通過狀態(tài)空間來描述非壽險(xiǎn)賠付過程，應(yīng)用卡爾曼濾波來估計(jì)狀態(tài)空間的轉(zhuǎn)換參數(shù)，并分別預(yù)測(cè)損失頻率和損失程度，從而動(dòng)態(tài)地估計(jì)未決賠款準(zhǔn)備金.SáNCHEZ［8］結(jié)合模糊回歸理論，利用模糊回歸方法評(píng)估未決賠款準(zhǔn)備金.這種方法比較適合于數(shù)據(jù)信息欠清晰的情形，但有時(shí)評(píng)估的計(jì)算量偏大.考慮到區(qū)間數(shù)界限分明、信息含量豐富的優(yōu)點(diǎn)，本文在鏈梯法的指數(shù)平滑型進(jìn)展因子基礎(chǔ)上，利用區(qū)間數(shù)回歸方法估計(jì)各發(fā)展年間的進(jìn)展因子，給出一種新的未決準(zhǔn)備金的評(píng)估方法.

1 預(yù)備知識(shí)

1.1 區(qū)間數(shù)的定義及其運(yùn)算

定義1A=［a，b］={x:a≤x≤b}稱為一個(gè)區(qū)間數(shù)，a和b分別稱為區(qū)間數(shù)的下限(左端點(diǎn))和上限(右端點(diǎn)).當(dāng)a=b時(shí)，區(qū)間數(shù)退化為一個(gè)實(shí)數(shù).區(qū)間數(shù)的全體記為I(R).區(qū)間數(shù)還可以表示成另一種形式:A=＜c(A)，r(A)＞.其中c(A)=)表示的是A的中點(diǎn)，也可稱為A的位置系數(shù)，反映了A的大小;r(A)=表示的是A的半徑，也可稱為A的不確定系數(shù)，反映了A的不確定程度.

定義2 稱n個(gè)有序區(qū)間數(shù)組X=(X1，X2，…，Xn)為n維區(qū)間向量，其中Xi∈I(?)，i=1，2，…，n.n維區(qū)間向量的全體記為I(?n).

定義3 對(duì)于任意X1，X2∈I(?)，X1=［，］，X2=［x2］，都有如下的運(yùn)算關(guān)系:，其中0 ?［x2］.

定義4 設(shè)存在X∈I(?)，X=［］.另外對(duì)于任意實(shí)數(shù)λ∈R有

1.2 區(qū)間數(shù)據(jù)的線性回歸方法

2000年BILLARD等［9］提出區(qū)間數(shù)據(jù)的線性回歸模型的 CM 方法.之后，NETO 等［10－11］對(duì) CM方法進(jìn)行改進(jìn)，提出CRM和CCRM的方法來擬合區(qū)間線性回歸方程.然而，上述模型的自變量和因變量都是區(qū)間數(shù).本文考慮自變量是精確值，而因變量是區(qū)間數(shù)的情況.

設(shè)有一個(gè)區(qū)間變量Y和P個(gè)實(shí)變量Xj，j=1，2，…，p，yi=［yi］，表示的是區(qū)間變量Y的第i次觀測(cè)值，xij=［xij］表示的是實(shí)變量Xj的第i次觀測(cè)值，i=1，2，…，n.則所有的樣本可以表示為如下的矩陣形式:

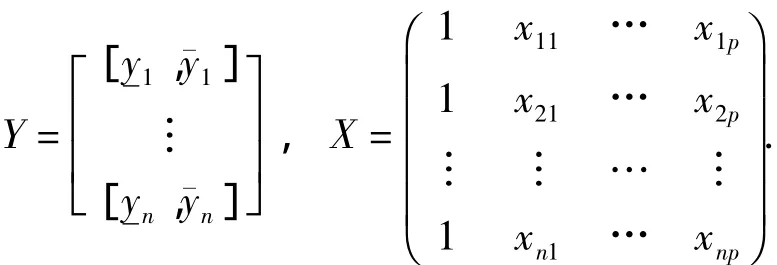
考慮如下形式的線性回歸方程:

其中，［βi］=［βi］，i=1，2，…，p是待估計(jì)系數(shù)，［，］是誤差項(xiàng).若將區(qū)間數(shù)等價(jià)地表示成中心和半徑的形式，即［Y］= ＜c［Y］，r［Y］＞，［βi］=＜c［βi］，r［βi］＞，［ε］= ＜c［ε］，r［ε］＞.那么，上述方程可以轉(zhuǎn)化成下面兩個(gè)線性回歸方程:

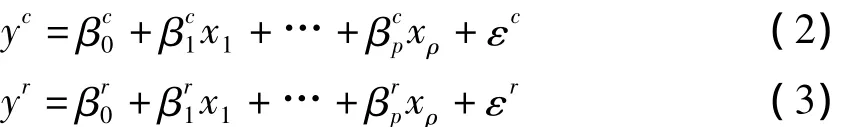
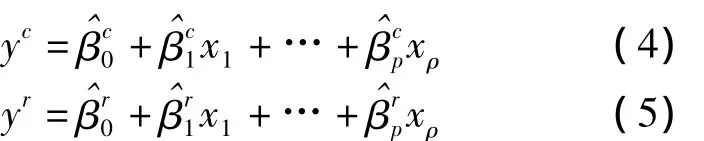
因此，［Y］的預(yù)測(cè)值可以寫成［］=［，］，其中=－

1.3 鏈梯法［12］

鏈梯法依賴每年的賠付數(shù)據(jù)，并用流量三角形形式將這些數(shù)據(jù)加以表述，見表1.Cij表示事故發(fā)生在第i年，而在第i+j年的賠付額.可將表1表示成累計(jì)賠付額流量三角形.用Dij代替Cij，其中根據(jù)鏈梯法的基本假設(shè)，各進(jìn)展年間的賠付額有穩(wěn)定的比例

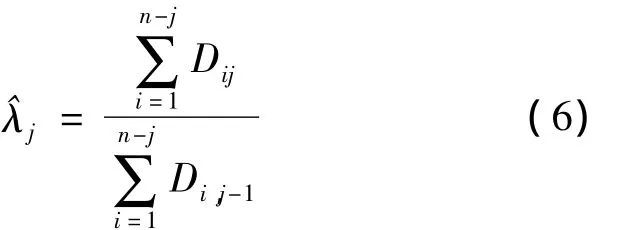
(j=1，2，…，n)稱為各個(gè)發(fā)展年間的進(jìn)展因子.因此，未來未決賠款準(zhǔn)備金的預(yù)測(cè)方程為

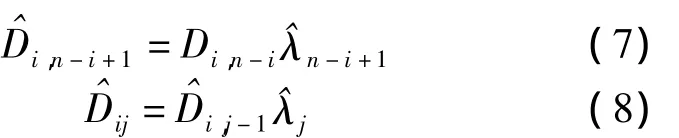
在得到累計(jì)賠款額估計(jì)值之后，可求未來n年的賠款增量.即:

因此，可求出未來未決賠款準(zhǔn)備金的總額V=

1.4 指數(shù)型進(jìn)展因子

為了避免估計(jì)參數(shù)過多的問題出現(xiàn)，引進(jìn)SHERMAN［3］的指數(shù)型進(jìn)展因子模型:

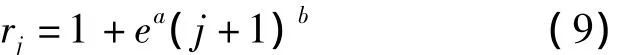
其中，rj(j=1，2，…，n)表示各進(jìn)展年的進(jìn)展因子.a和b是待估參數(shù).方程(9)等價(jià)于如下線性方程:

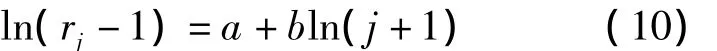
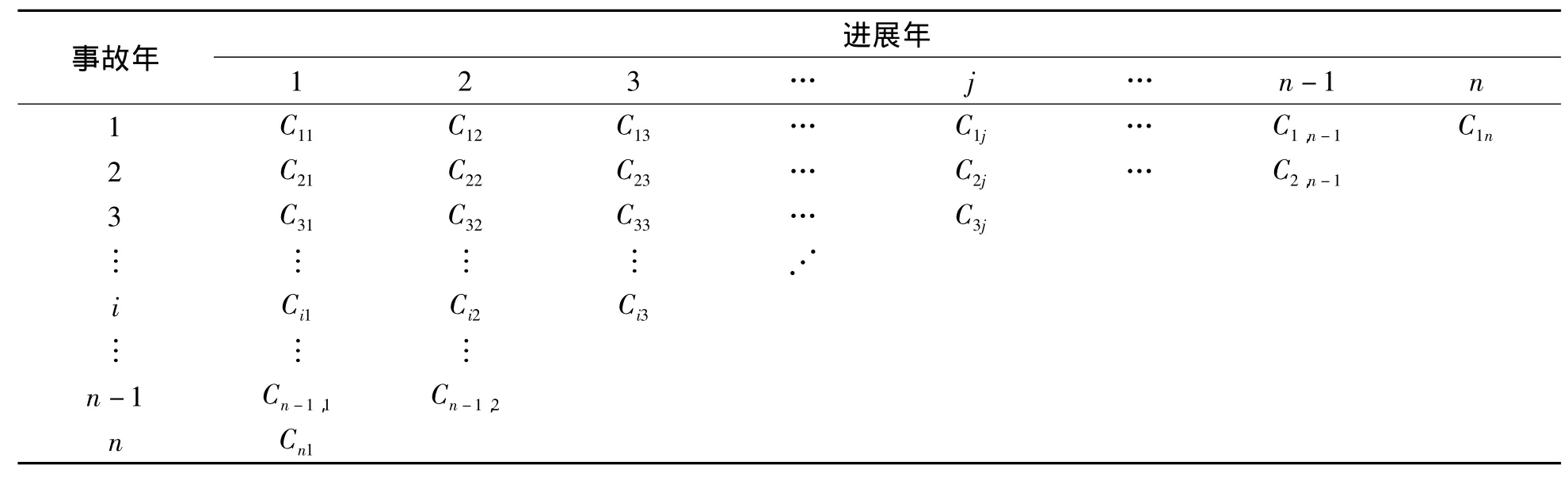
表1 流量三角形Table 1 Run－off triangle

2 區(qū)間數(shù)回歸估算法及其應(yīng)用

2.1 區(qū)間數(shù)回歸估算法

結(jié)合流量三角形的數(shù)據(jù)特點(diǎn)，為充分利用數(shù)據(jù)信息，將方程(10)轉(zhuǎn)換成一個(gè)區(qū)間數(shù)回歸模型:

其中，Rj=ln(Min{r1j，r2j，…，rn－j，j}－1)，=ln(Max{r1j，r2j，…，rn－j，j}－ 1)，j=1，2，…，n.［a，a］和［b］是待估系數(shù)，［ε，］是一個(gè)誤差項(xiàng).利用NETO等［10－11］提出的區(qū)間數(shù)回歸方程參數(shù)估計(jì)理論，將模型(11)轉(zhuǎn)化成如下兩個(gè)線性回歸方程:

將上述區(qū)間數(shù)回歸方法應(yīng)用于未決賠款準(zhǔn)備金評(píng)估，可分為以下4步:

(1)根據(jù)累計(jì)賠款流量三角形算出鏈接比三角形，如表2.

表2 鏈接比三角形Table 2 Link ratio triangle

(2)應(yīng)用區(qū)間數(shù)回歸方法計(jì)算各發(fā)展年間的進(jìn)展因子.在計(jì)算出鏈接比三角形后，將各年的進(jìn)展因子ri，j轉(zhuǎn)化成區(qū)間數(shù)形式，即Rj=ln(Min{r1j，r2j，…，rn－j，j}－1)=ln(Max{r1j，r2j，…，rn－j，j}－1)，這樣得到了1組區(qū)間數(shù)［Rj，］.根據(jù)區(qū)間數(shù)，［，］［，］.r=回歸方法 估計(jì)出參數(shù) 和 根據(jù)j1+ea(j+1)b，計(jì)算出=1+(j+1)和=1+(j+1)，為了簡(jiǎn)化計(jì)算過程，可令區(qū)間數(shù)的期望作為進(jìn)展因子的估計(jì)值

(3)確定發(fā)展因子.當(dāng)j≤s時(shí)，定義表示的是發(fā)展年j到s的發(fā)展因子.

(4)預(yù)測(cè)未來累計(jì)賠償金.根據(jù)鏈梯法的原則，可以得出未來累計(jì)賠償金的計(jì)算公式:

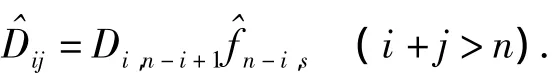
2.2 實(shí)際應(yīng)用分析

(1)賠款數(shù)據(jù)集

表3中的數(shù)據(jù)來源于某財(cái)產(chǎn)保險(xiǎn)公司長(zhǎng)尾業(yè)務(wù)的賠款數(shù)據(jù)，數(shù)據(jù)單位是萬元.縱向表示的是事故發(fā)生年，橫向表示的是事故發(fā)生后的進(jìn)展年.各賠款數(shù)據(jù)表示的是賠款增量的流量三角形，為了方便計(jì)算，將表3轉(zhuǎn)換成累積賠款流量三角形的形式(表4).

(2)估算結(jié)果

依表4數(shù)據(jù)，利用EXCEL得出鏈梯法的未來未決賠款準(zhǔn)備金估算結(jié)果見表5.

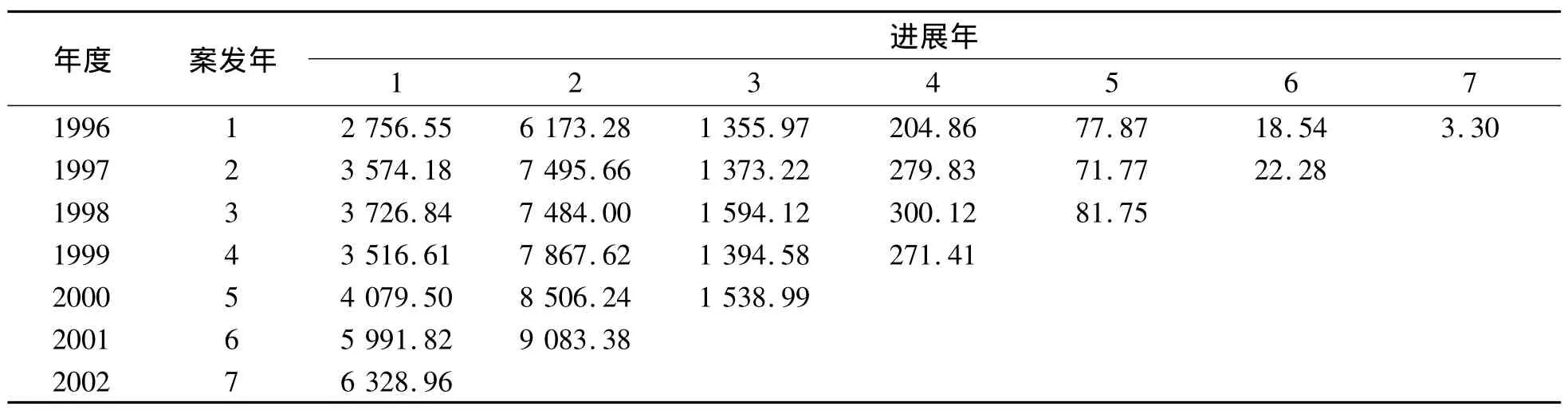
表3 賠款增量數(shù)據(jù)集Table 3 Claim incremental data set

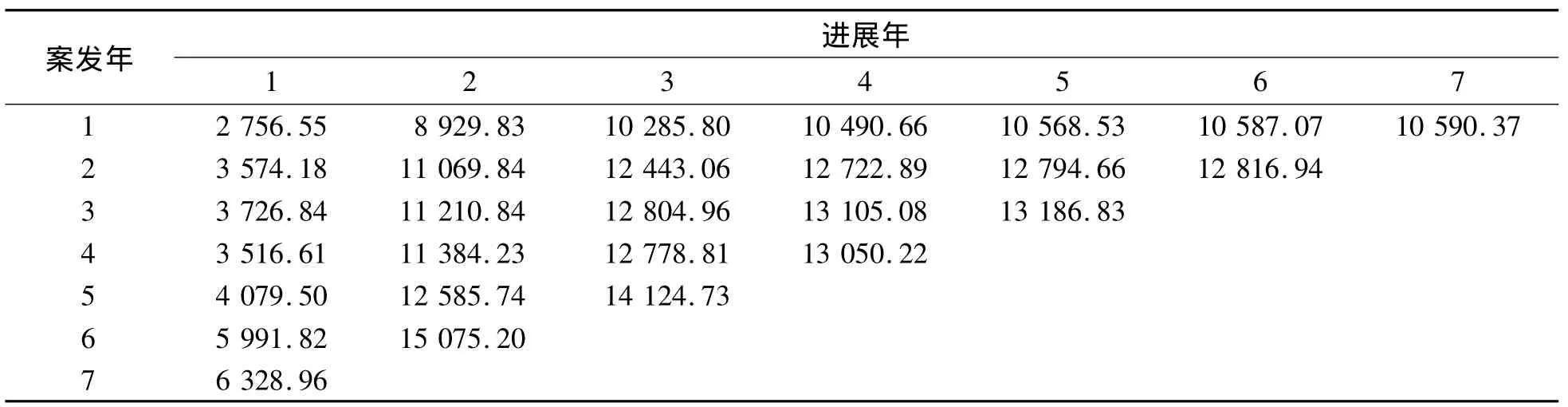
表4 累積賠款流量三角形Table 4 Cumulative claim run－off triangle

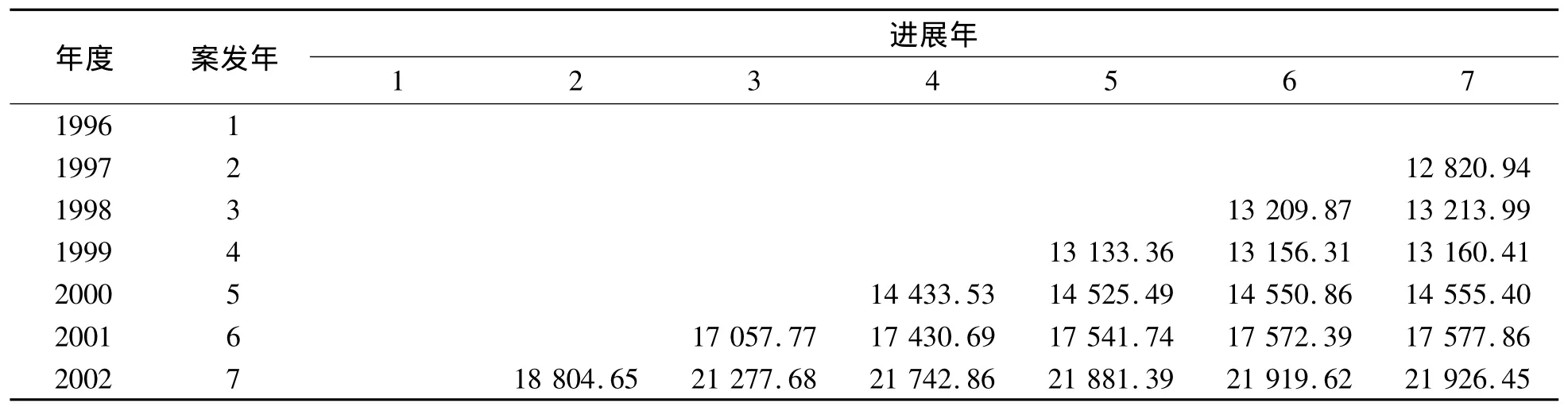
表5 鏈梯法結(jié)果Table 5 The results of chain ladder method

根據(jù)表4的數(shù)據(jù)，計(jì)算出鏈接比三角形(表6).

在表6中，令Rj=ln(Min{r1j，r2j，…，rn－j，j}－1)，=ln(Max{r1j，r2j，…，rn－j，j}－1)，得到了1組區(qū)間數(shù)據(jù)，利用區(qū)間數(shù)據(jù)回歸方法，經(jīng)SPSS軟件估計(jì)［］，j=1，2，…，6.結(jié)果如下:

j

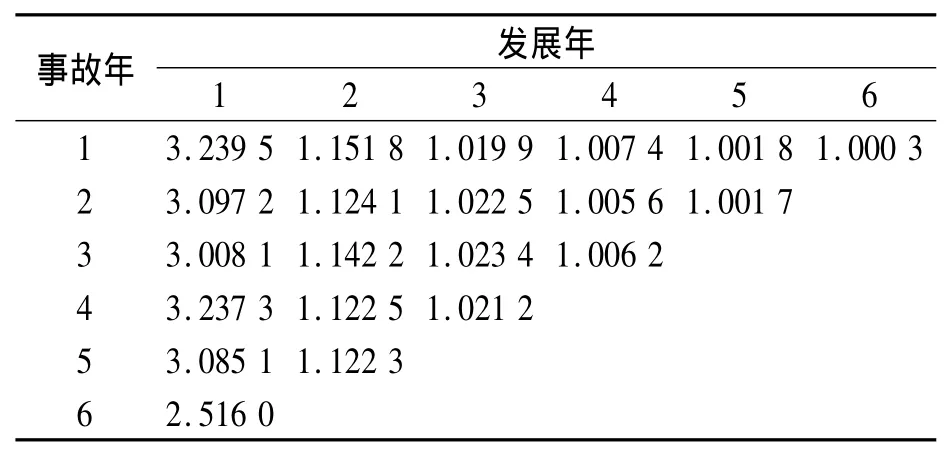
表6 實(shí)際數(shù)據(jù)中的鏈接比三角形Table 6 Run－off triangle in our numerical applications

為了簡(jiǎn)化計(jì)算過程，令區(qū)間數(shù)的期望E(［，，

，其作為進(jìn)展因子的估計(jì)值通過EXCEL計(jì)算出未來未決賠款準(zhǔn)備金的結(jié)果見表7.

根據(jù)表5和表7可以計(jì)算出2003年至2008年的賠款增量見表8.

由表8可見，后幾年的增量賠款額逐年減少，且減少幅度越來越小，恰好符合Sherman的指數(shù)型發(fā)展模型.

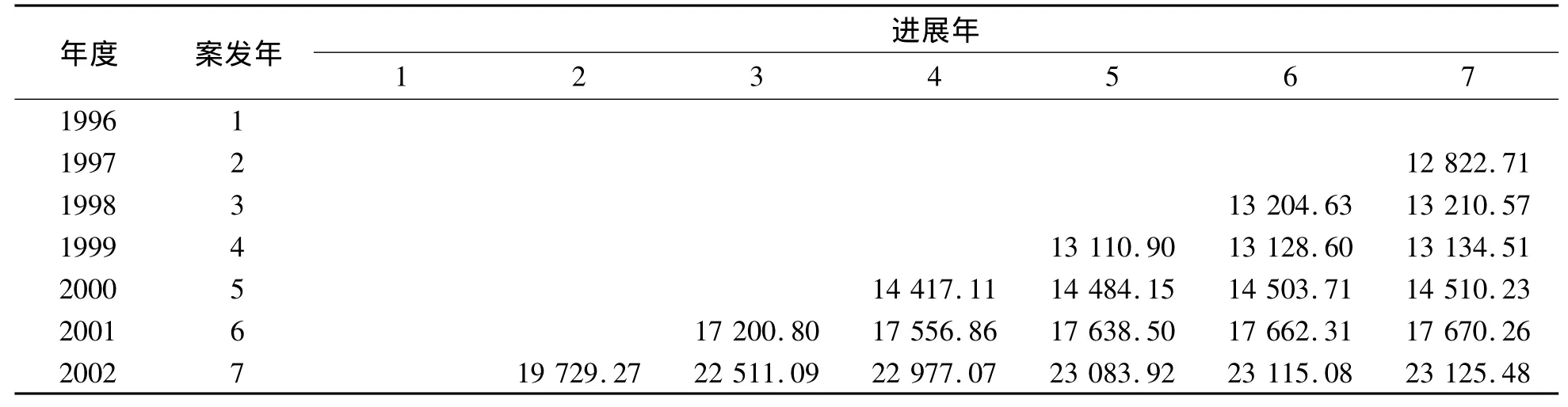
表7 區(qū)間回歸模型計(jì)算結(jié)果Table 7 The results of interval regression model

表8 2003～2008年的賠款增量估計(jì)值Table 8 The estimate of claim incremental from 2003 to 2008

(3)對(duì)比分析

在計(jì)算過程中，表4中第6行第2列的數(shù)據(jù)明顯與其他數(shù)據(jù)相差較大，可認(rèn)為此項(xiàng)為異常值.為了能夠比較合理地反應(yīng)結(jié)果，可利用平均值去代替這個(gè)異常值.此外，在對(duì)比鏈梯法和區(qū)間回歸方法的優(yōu)劣時(shí)，本文做了如下的誤差分析.用兩種方法估計(jì)出來的值減去相應(yīng)年份的實(shí)際賠償額作為誤差值，結(jié)果見表9.表9顯示，區(qū)間數(shù)回歸方法的估計(jì)值與實(shí)際值相差較小，比鏈梯法的估計(jì)誤差明顯降低.

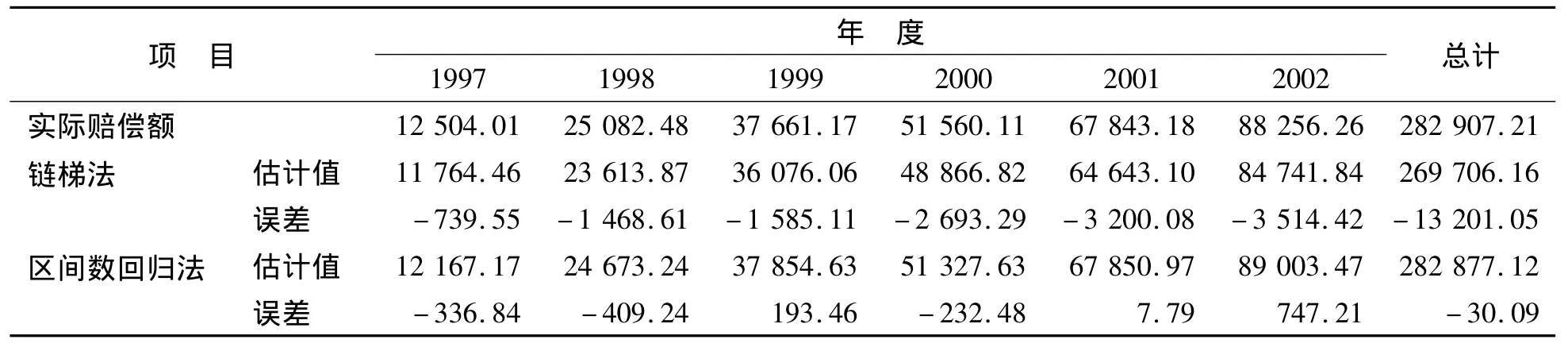
表9 鏈梯法與區(qū)間回歸模型的結(jié)果分析Table 9 The analysis results of chain ladder method and interval regression model

3 結(jié)束語

本文嘗試用區(qū)間數(shù)回歸模型估算非壽險(xiǎn)未決賠款準(zhǔn)備金，所得結(jié)果表明區(qū)間數(shù)回歸模型法相對(duì)于傳統(tǒng)的鏈梯法估計(jì)效果有一定優(yōu)勢(shì).鏈梯法易受異常值影響，估計(jì)誤差通常較大.而區(qū)間數(shù)回歸模型方法在缺乏分布模型的條件下，結(jié)合區(qū)間數(shù)回歸的相關(guān)理論，充分挖掘和利用數(shù)據(jù)信息，從數(shù)據(jù)真實(shí)反映出險(xiǎn)理賠規(guī)律.這種方法可較好地排除異常值的影響，且計(jì)算簡(jiǎn)便.

［1］ KREMER E.IBNR claims and the two way model of ANOVA［J］.Scand Actuar J，1982，1:47－55.

［2］ MACK T.A simple parametric model for rating automobile insurance or estimating IBNR claims reserves［J］.Astin Bull，1991，21(1):93－109.

［3］ SHERMAN R E.Extrapolating，smoothing and interpolating development factors［J］.Proc Casu Actuar Sci，1984，71:122－123.

［4］ RENSHAW A E，VERRALL R J.A stochastic model underlying the chain ladder technique［J］.Brit Actuar J，1998，4(4):903－923.

［5］ 孟生旺.非壽險(xiǎn)準(zhǔn)備金評(píng)估的廣義線性模型［J］.統(tǒng)計(jì)與信息論壇，2009，24(6):3－7.MENG S W.Generalized linear models and their applications in non－life insurance loss reserving［J］.Stat Inform Forum，2009，24(6):3－7.

［6］ 盧志義，劉樂平.廣義線性模型在非壽險(xiǎn)精算中的應(yīng)用及其研究進(jìn)展［J］.統(tǒng)計(jì)與信息論壇，2007，22(4):26－31.LU Z Y，LIU L P.The applications of generalized linear models in non－life insurance and their development［J］.Stat Inform Forum，2007，22(4):26－31.

［7］ 陳迪紅，陳睿.卡曼濾波在非壽險(xiǎn)未決賠款準(zhǔn)備金估算中的應(yīng)用［J］.系統(tǒng)工程，2009，27(1):77－81.CHEN D H，CHEN R.Application of Kalman filter in estimating non－life outstanding claims reserving［J］.Syst Engin，2009，27(1):77－81.

［8］ SáNCHEZ J A.Calculating insurance claim reserves with fuzzy regression［J］.Fuzzy Sets Syst，2006，157:3091－3108.

［9］ BILLARD L，DIDAY E.Regression analysis for interval－valued data［M］.Berlin:Springer－Verlag，2000:369－374.

［10］ LIMA N E A，CARVALHO F A T.Center and range method for fitting a linear regression model to symbolic interval data［J］.Comput Statist Data Anal，2008，52:1500－1515.

［11］ LIMA N E A，CARVALHO F A T.Constrained linear regression models for symbolic interval－valued variables［J］.Comput Statist Data Anal，2010，54:333－347.

［12］張博.精算學(xué)［M］.北京:北京大學(xué)出版社，2005.

ZHANG B.Actuarial science［M］.Beijing:Peking University Press，2005.

［13］張琳，王軼銘.未決賠款準(zhǔn)備金評(píng)估模型研究［J］.江西財(cái)經(jīng)大學(xué)學(xué)報(bào)，2006，45(3):41－44.ZHANG L，WANG Y M.The research of outstanding claims reserve evaluation model［J］.J Jiangxi Finan Univ，2006，45(3):41－44.