有限維空間上的橢圓框架

陳茜茜，孟彬

(1．無錫市輔仁高級中學，江蘇無錫 214000;2．南京航空航天大學數學系，江蘇南京 210016)

0 引言

Hilbert空間中框架概念最早是Duffin和Schaeffer［1］在1952年提出，當時主要用來研究非調和Fourier分析．1986年，Daubechies，Grassmann［2］等把框架理論應用于小波分析的研究并取得了突破性的進展，使得框架理論受到廣泛的關注，也吸引了眾多學者投身這一領域的研究．Han，Larson［3］等把算子理論的方法應用到框架的研究上，得到了豐碩的成果，也形成了一個主要的研究方向．目前，框架不僅應用在小波分析中，在信息編碼、量子計算等領域也有重要的應用價值．

在量子信息中，主要用到的是有限維空間上的框架，稱之為有限維框架．在各類有限框架中，人們發現具有等范數的框架有重要的應用［4］．事實上，在數據包編碼中，等范數的框架是在一個數據包丟失下最優的［5］．因此，許多學者重點研究了這一類框架．等范數框架相當于所有框架向量都在一個圓上，在本文中，將研究更廣泛的一類框架——橢圓框架，即框架都在一個橢圓上．

1 預備知識

設H是一個有限維的Hilber空間．B(H)表示H上有界線性算子的全體．首先介紹一些關于框架的基本概念和基本性質．

定義1 設{xi}ki=1?H，若存在兩個正數A，B＞0，使得

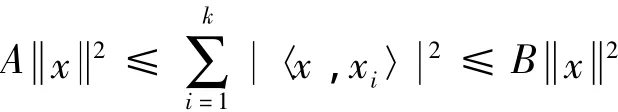
則稱{xi}ki=1為H的框架，其中A，B分別稱為框架下界，上界．

若A=B，則稱{xi}ki=1為緊框架;若A=B=1，則稱其為Parseval框架．

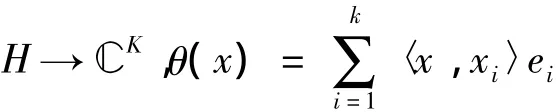
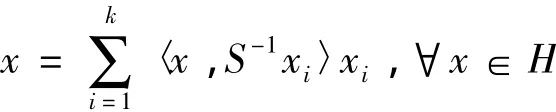
容易看出θ是單射，S是一個正的可逆線性算子．在解碼過程中，需要用到對偶框架．

定義2 設{xi}ki=1與{yi}ki=1都是H的框架，若滿足:

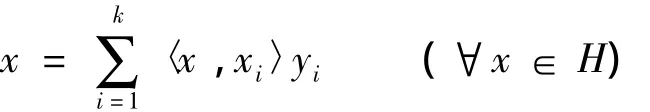
則稱{xi}ki=1與{yi}ki=1互為對偶框架．

對于框架{xi}ki=1，其中一個特殊的對偶框架是{S－1xi}ki=1，稱之為典則對偶．

一個橢圓就是單位圓在可逆線性算子作用下的像．令S1={x:x=1}，設T∈B(H)是一個可逆線性算子，?T:=T(S1)，稱為橢圓表面．如果一個框架{xi}ki=1的所有框架向量xi都在同一個橢圓表面上，就稱這個框架是橢圓框架．顯然，{xi}ki=1是橢圓框架當且僅當{xi}ki=1是框架并且存在可逆線性算子V∈B(H)使得 V(xi)=1，i=1，2，…，k．K．Dekema［6］等人證明了橢圓緊框架的存在性，并利用投影算子刻畫了橢圓框架．本文主要研究橢圓框架本身的一些性質，例如對偶，等價問題．

事實上，橢圓也可以由正可逆線性算子來決定．設T∈B(H)是可逆線性算子，由極分解定理，T=UT1，其中U是酉算子，T1是可逆正算子，顯然?T=?T1．

對于標準橢圓上的緊框架，有下面的結論:

小李暗笑了幾聲，丁主任接住話：我的確有，而且營業部所有人里，就我和張大爺才有這倉庫和大門的鑰匙，所以我和張大爺好像給大家添麻煩了。

定理1 設H是n維Hilbert空間，{x1，x2，…，xk}是H中的以a為框架界的緊框架，且橢圓向量都在標準橢圓:a1y21+a2y22+… +any2n=1上，其中ai≥0，i=1，2，…，n．令r=a1+a2+… +an，則a=m r．

證明 令 xi=(ξ1i，ξ2i，…，ξni)T，i=1，2，…，k，則:

另一方面，由于{xi}ki=1是以a為界的緊框架，所以θ*θ=aI，其中θ是{xi}ki=1的分析算子．這樣又有:

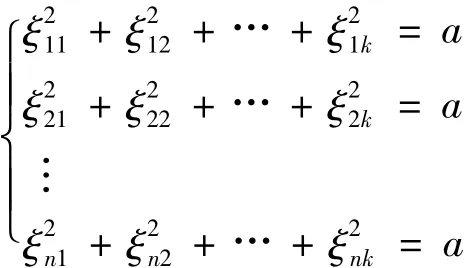
于是(a1+a2+… +an)a=k，從而得到:a=k r

2 主要結論

先考慮任給一個框架，是否都有橢圓Parseval框架．事實上，有下面的結果:

定理2 設{xi}ki=1是H的框架，設存在k－維Hibert空間K?H和K中的一組標準正交基{ei}ki=1，以及一個從K到H上的投影Q∈B(K)，使得Qei=xi(i=1，2，…，k)．若存在一個H上的可逆線性算子T使得 T－1PQ*ei=1，其中P是K到H上的正交投影，則{xi}ki=1在橢圓?T上有Parseval對偶框架．

證明 令yi=PQ*ei(i=1，2，…，k)，說明{yi}ki=1與{xi}ki=1是對偶的，事實上，?x∈H，有:

另一方面，還要說明{yi}ki=1是H中的Parseval框架，事實上，對于任意x∈H有

這樣，就證明了結論．

對于H的兩個框架{xi}ki=1，{yi}ki=1，若存在可逆線性算子L，使得Lxi=yi，i=1，2，…，k，則稱這兩個框架是相似的．

定理3 設{xi}ki=1是橢圓框架，S是其框架算子，則{S－1xi}ki=1是唯一與{xi}ki=1對偶相似的橢圓框架．

證明 顯然{S－1xi}ki=1是{xi}ki=1的對偶框架，且它也是橢圓框架并且與{xi}ki=1相似．

設{yi}ki=1是與{xi}ki=1對偶且相似的框架，則存在可逆線性算子L，使得yi=Lxi，i=1，2，…，k，令T=LS，則對任意x∈H有:

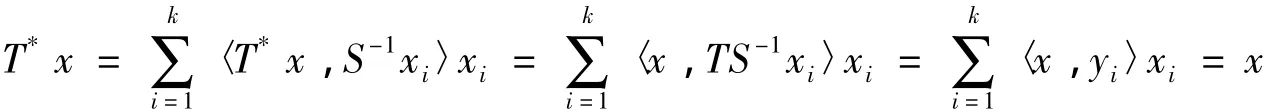
所以 T*=I，從而 L=S－1，所以 yi=S－1xi(i=1，2，…，k)．

定理4 設{xi}ki=1，{yi}ki=1是H上的兩個橢圓框架，且存在H上的同一個可逆線性算子T，使得xi=T?i，yi=Tηi，其中: ?i=1 ， ηi=1，i=1，2，…，k．若{?i}ki=1與{ηi}ki=1是相互正交的框架，且 ?i+ηi對任意i=1，2，…，k是正常數．則{xi+yi}ki=1也是橢圓框架．

證明 設{xi}ki=1的上下框架界分別為B1，A1，其框架算子為S1．設{yi}ki=1的上下框架界分別為B2，A2，其框架算子為S2．則對任意x∈H，有:

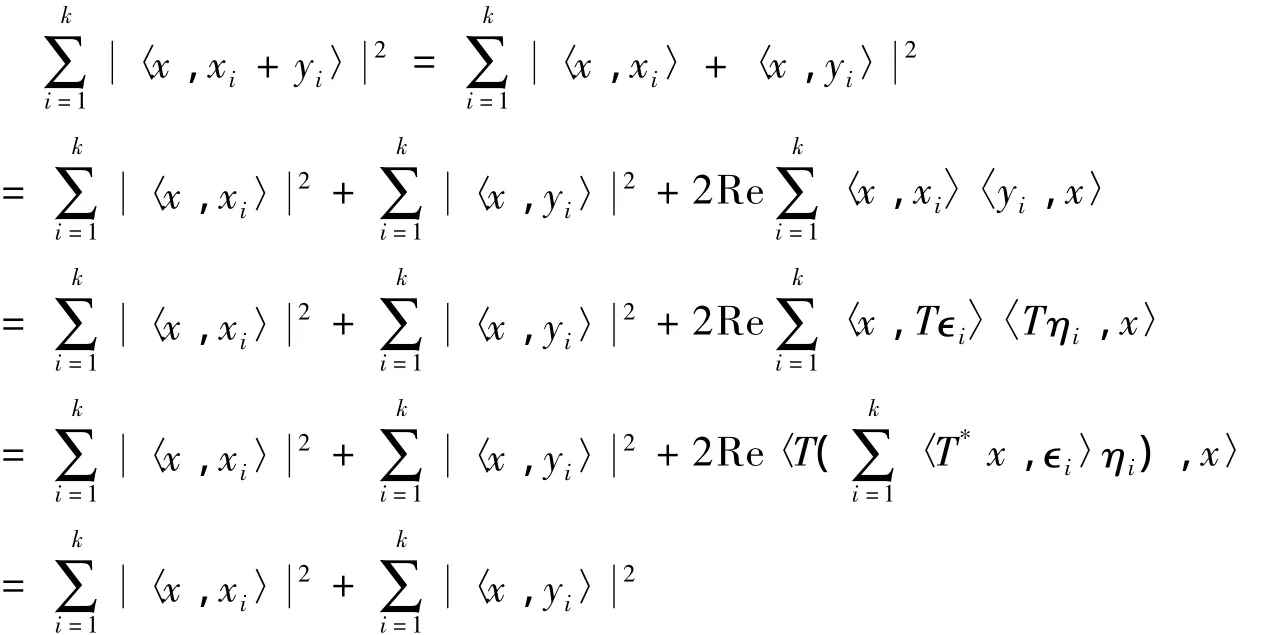
所以{xi+yi}ki=1是框架，其上下框架分別是B1+B2，A1+A2．另一方面，xi+yi=T(?i+ηi)，而 ?i+ηi，i=1，2，…，k是正常數，因此{xi+yi}ki=1是橢圓框架．