利用幾何畫板“測量”功能探究勾股定理
周偉
中圖分類號:G633.6 文獻標識碼:B 文章編號:1672-1578(2016)01-0334-01
幾何畫板具有很高的運算能力和高分辨率以及完善的彩色繪圖功能,可以通過輸入參數,賦予圖形千變萬化,通過對圖形的收集整理,可促進發現問題,提出猜想,進行驗證.幾何畫板為幾何圖形的性質探究提供了知識交流,方法探究的可變化平臺.尋找數學與幾何畫板的切入點,發揮幾何畫板的優勢,使抽象的概念具體化,使微觀的過程宏觀化.幾何畫板使其結構得以量化。
利用測量功能,測得圖形面積,從而得出結論,如下例:
在勾股定理應用的探究活動中,先利用幾何畫板做出圖(見圖1.1).
畫圖步驟:
(1)打開幾何畫板,新建畫板.單擊"自定義工具",選定"三角形工具"中的"直角三角形",并在新畫板中畫出任意直角三角形△ABC,其中∠B=90°。
(2)以BC為邊,畫出正方形BCDE.同時選定點B以及直線BC,點擊構造中的垂線.以點B為圓心,以BC為半徑畫圓,交垂線與點E,同理可以得出點D.連接直線CD、DE、EB.則得出正方形BCDE。
(3)同理,得出正方形CAHK和正方形ABFG。
利用幾何畫板的測量功能對三個正方形的面積進行度量測得出面積KHAC=5.96cm2,面積DCBE=3.99cm2,面積BAGF=1.97cm2,通過三個面積之間的關系可以發現SAHKCSABFCSCBED。
接下來連接EF、GH、KD,分別以EF、GH、KD為邊作正方形ELMF、GNOH、KPQD,具體方法參見步驟2).再連接MN、OP、QL(見圖1.2)。
1.猜想
(1) △ABC、△DCK、△EBF、△AGH這四個三角形面積有什么關系?
(2) 四邊形DELQ、FGNM、HOPK是什么四邊形, 它們分別與上述四個三角形有什么關系?
(3) 正方形QDKP、ELMF、GMOH的面積有什么關系?
2.驗證猜想
利用測量功能對上述猜想中的三角形、四邊形的面積分別進行測量,通過討論交流可以從圖4.2得出以下結論:B△ABC=S=△DCK=S△AGH,四邊形SDELQ=SFGNM=SHOKP,任意一個梯形的面積是上述任意一個三角形面積的5倍.又因為正方形QDKP、ELMF、GNOH的面積中,不存在兩個小正方形面積的和等于大正方形的面積,所以DK、EF、GH不滿足勾股定理。
3.任意拖動C點在平面上運動,將直角三角形改為任意三角形ABC,重復以上的步驟,可以發現上述結論仍然成立
在上述探究過程中,通過測量,可以認識和掌握數學科學研究方法,深入理解數學真理是非常有益的.利用幾何畫板的測量功能進行測量探究可分為:隨意測量探究,實驗測量探究,有規律的測量探究。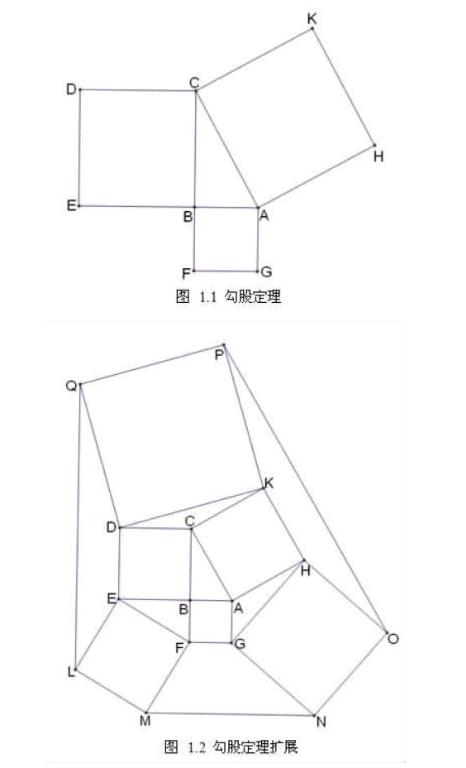
幾何畫板的"拖動"和"測量"功能使"靜態"的圖形"動態"化,化宏觀為微觀,化抽象為具體.幾何畫板所具備的突出特點為數學過程中實施新的教學理念搭建一個理想的平臺,為課堂教學注入生命的活力。

