結(jié)合歐拉矢量的反演算法構(gòu)建青藏高原東北緣地殼運動速度場模型

結(jié)合歐拉矢量的反演算法構(gòu)建青藏高原東北緣地殼運動速度場模型

王帥， 張永志， 姜永濤

(長安大學(xué)地質(zhì)工程與測繪學(xué)院，陜西 西安710054)

摘要：探討地殼運動速度場模型的構(gòu)建方法，提出結(jié)合歐拉矢量的維多樣性動態(tài)權(quán)重粒子群算法構(gòu)建地殼運動速度場模型。通過模擬算例驗證該算法的穩(wěn)定性和有效性，建立的速度場模型與線性權(quán)重粒子群算法和非線性權(quán)重粒子群算法的計算結(jié)果相比具有較高的精度，且收斂速度較快。利用青藏高原東北緣1999—2013年中國地殼運動觀測網(wǎng)絡(luò)觀測到的GPS水平速率結(jié)果，在塊體劃分和模型辨識的基礎(chǔ)上，建立青藏高原東北緣地殼運動速度場模型，并將其與最小二乘配置法的計算結(jié)果進行比較，結(jié)果表明改進的粒子群算法建立的地殼運動速度場模型具有較高的精度。

關(guān)鍵詞：地殼運動； 速度場模型； 粒子群算法； 青藏高原東北緣； 反演

收稿日期：*2014-05-14

基金項目：國家自然科學(xué)基金(41374028,40674001)；國土資源大調(diào)查項目(1212010914015)；陜西省教育廳自然科學(xué)科研項目(12JK0798)

作者簡介：王帥(1988-)，男，河南新鄉(xiāng)人，碩士研究生，研究方向：地殼形變與地球動力學(xué).E-mail：wang0814082shuai@163.com.

中圖分類號:P315.72+5文獻標志碼：A

DOI:10.3969/j.issn.1000-0844.2015.01.0214

UsinganInversionAlgorithmwithEulerVectorto

ConstructaModeloftheCrustalMovementVelocity

FieldintheNortheasternMarginoftheTibetanPlateau

WANGShuai，ZHANGYong-zhi，JIANGYong-tao

( School of Geology Engineering and Geomatics，Chang’an University，Xi’an，Shaanxi710054，China)

Abstract：Many methods and models have been used to construct crustal movement velocity fields，including Least Squares Collocation，multi-surface functions，spherical harmonics methods，spherical discontinuous deformation analysis，and finite element methods，all of which have certain premise conditions or application scope.Based on the Euler vector，we put forward a new particle swarm optimization (PSO) algorithm from which block motion and strain tensor parameters can be determined by inversion，and then a regional crustal movement velocity field can be constructed.Simulation test results showed that this improved PSO is stable and effective. When the iteration reached 20 times，the improved PSO results were close to their optimal values，while the other two algorithms continued to search.The precision of the velocity field constructed by this method is much higher than that from linear and nonlinear PSOs.A comparison of the effectiveness and lack of bias of the displacement calculated by different methods indicated that the accuracy of the velocity model calculated by the improved PSO was the highest，and the variance and mean value of its residuals were much smaller.Based on GPS observational results from the northeastern margin of the Tibetan Plateau from 1999 to 2013，for which coseismic disturbance has been considered on the basis of block division and model identification evaluated by unbiased and effectiveness rules，the crustal movement velocity field was determined using the improved PSO.The residual characteristics that closely followed a normal distribution indicated that the velocity field calculated by the improved PSO was reliable and without systematic error.A comparison with the results calculated by Least Squares Collocation was performed，which indicated that the new PSO algorithm effectively and accurately established the crustal movement velocity field.From the constructed velocity field，a significant difference can be seen in how the northeastern margin of the Tibetan Plateau crust moves；the velocity decreases from south to north with clockwise rotation.The NE motion is blocked by the relatively stable Alashan block，which is creating mountain uplift and basin subsidence in the region.

Keywords：crustalmovement；velocityfieldmodel；particleswarmoptimization；northeasternmarginoftheTibetanPlateau；inversion

0引言

中國大陸地殼運動持久、強烈、廣為發(fā)育，是我國高山巍峨、大河?xùn)|流的緣由，也是地震頻繁、災(zāi)害沉重的起因[1]。高精度、大范圍和準實時的GPS地殼運動觀測數(shù)據(jù)為獲取復(fù)雜的地殼形變信息，研究構(gòu)造變形過程中陸地變遷、災(zāi)害與環(huán)境演化的力源體系提供了必要條件，在地學(xué)研究中廣為應(yīng)用[2-4]。地殼運動與變形直接反映地球內(nèi)部物質(zhì)的運移及構(gòu)造應(yīng)力場變化[5]，為了獲得相對均勻分布的地殼運動速度場模型，國內(nèi)外學(xué)者對GPS位移資料的地殼運動速度場模型的建立方法進行了深入的研究。El-Fiky等[6]應(yīng)用最小二乘配置法建立了日本Tohoku地區(qū)的地殼運動速度場模型。Holt等[7]利用雙三次樣條函數(shù)模擬了亞洲局部區(qū)域的地殼運動速度場。王澤民等[8]利用球面非連續(xù)變形分析(DDA)模型計算了中國大陸地殼運動速度場。蔣志浩等[9]利用有限元插值法計算了中國大陸CGCS2000下的地殼運動速度場模型。刁法啟等[10]利用綜合逼近法探討了地殼運動速度場的構(gòu)建方法。劉經(jīng)南等[11]將多面函數(shù)法用于中國大陸速度場模型的建立。石耀霖等[12]提出了速度場模型建立的球諧函數(shù)擬合法。

除此之外，大地測量反演方法在地殼運動速度場模型建立中也得到了應(yīng)用，Haines等[13]研究了利用應(yīng)變張量反演地殼運動速度場模型的方法；至此，GPS位移資料、地震矩張量的地殼運動速度場反演理論和方法得到了系統(tǒng)的發(fā)展和應(yīng)用[14-17]，為地殼運動速度場模型的建立提供了一種新的思路。粒子群算法(PSO)廣泛用于解決地球物理反演中的非線性問題，本文在對粒子群算法深入研究的基礎(chǔ)上，基于混沌變異思想，提出了維多樣性的動態(tài)權(quán)重粒子群算法，在模擬算例分析的基礎(chǔ)上，以青藏高原東北緣為例，結(jié)合區(qū)內(nèi)各塊體滿足的塊體運動模型，采用GPS數(shù)據(jù)構(gòu)建一種塊體運動和應(yīng)變參數(shù)的反演方法，試圖減少模型建立過程中的復(fù)雜程序，快速簡便地獲取可靠的地殼運動速度場模型。

1維多樣性的動態(tài)權(quán)重粒子群算法

1.1標準粒子群算法

楊維等[18]詳細論述了粒子群算法的基本原理，D維粒子位置和速度的迭代過程可表示為

其中：a=c1r1(pbi-xi)+c2r2(gb-xi)；υnext和xnext分別為迭代k次時粒子i第d維的速度和位置；pbi為粒子i在k次迭代過程中第d維的最優(yōu)位置；gb為整個粒子群在k次迭代過程中第d維的最優(yōu)位置；ω為慣性權(quán)重因子；c1、c2為學(xué)習(xí)因子，本文取為2；r1和r2為[0，1]之間均勻分布的隨機數(shù)。

1.2維多樣性的動態(tài)權(quán)重粒子群算法

考慮到標準粒子群算法收斂速度較慢，容易陷入局優(yōu)，本文通過以下四個步驟對最優(yōu)解搜索過程中的權(quán)重因子進行改進。

(1) 動態(tài)權(quán)重因子。權(quán)重因子可以調(diào)整和控制粒子的速度，粒子各維的動態(tài)權(quán)重可通過pbi和gb合成的優(yōu)勢向量與粒子的當前速度來表示[19]

其中：M表示總的迭代次數(shù)；k表示當前迭代次數(shù)；ωmax和ωmin分別為最大和最小慣性權(quán)重，本文分別取為0.9和0.1。

(2) 維多樣性的度量指標。迭代初期，粒子在各維上的分布不盡相同，各維粒子隨迭代次數(shù)的增加趨于聚集，用該維上粒子位置的平均間距表示粒子的聚集程度，依此作為維多樣性的度量指標[20]

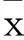
(3) 權(quán)重轉(zhuǎn)換策略。考慮到算法迭代到一定次數(shù)時粒子的維多樣性變差，可能陷入局優(yōu)。本文設(shè)定前M/2迭代次數(shù)時采用式(4)的權(quán)重因子策略，后M/2迭代次數(shù)時采用線性遞減權(quán)重策略式(7)，以增強算法的搜索能力，避免重復(fù)搜索[21]。

(4) 變異條件。后M/2迭代過程中，對維多樣性小于閥門值D(j)的粒子，根據(jù)Tent映射(式(9))對粒子重新初始化。

其中，xj，max，xj，min為第j維粒子坐標的上下限，abs()為絕對值函數(shù)。

初始化的具體步驟為[19]：

(Ⅰ) 混沌變量初始值。由(gbj-aj)/(bj-aj)將gbj轉(zhuǎn)化為混沌變量zz1j；

(Ⅱ) 生成混沌序列。把zz1j作為初始值，利用式(9)生成粒子第j維的序列zz2j，zz3j，…，zzNj；

(Ⅲ) 初始化結(jié)果。將zzij利用aj+(bj-aj)×zzij得到xij，其中i=1，2，…N；bj和aj分別為粒子搜索過程中設(shè)定的第j維位置的上、下限。按照式(1)和式(2)，對重新初始化后的粒子繼續(xù)迭代計算，即可求出滿足相應(yīng)迭代條件的粒子最優(yōu)解。

2模擬算例

本節(jié)模擬數(shù)據(jù)由李延興等[22]的整體旋轉(zhuǎn)與均勻應(yīng)變彈性方程利用表1參數(shù)計算給出，并在結(jié)果中加入隨機噪聲(期望為0，方差為1)作為觀測誤差，以此檢驗算法的抗噪能力。為了檢驗本文算法的有效性和穩(wěn)定性，采用以下三種不同定權(quán)方式的PSO算法反演歐拉和應(yīng)變張量參數(shù)，并對位移進行正演(模擬)計算， 計算結(jié)果如圖1所示。

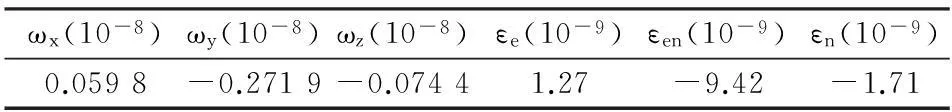
表 1　歐拉和應(yīng)變張量參數(shù)理論值

方案一：線性權(quán)重策略，ω=ωmax-k(ωmax-ωmin)/M。

方案二：非線性權(quán)重策略，ω=0.729×atan(1.0×(M-k)/M)。

方案三：維多樣性的動態(tài)權(quán)重策略。

通過比較位移模擬值和理論值之間的擬合效果來檢驗本文算法的穩(wěn)定性和有效性(不失一般性，本文僅對東向分量進行分析)。從圖1看出，改進的PSO算法收斂速度最快，當?shù)螖?shù)達到20次時反演結(jié)果已趨近于理論值，而其他兩種PSO算法仍在搜索中；隨著迭代次數(shù)的增加，方案一和方案二的反演結(jié)果得到了明顯的改善，但結(jié)合表2可以看出，方案一和方案二的反演結(jié)果與理論值仍有較大的差異，迭代到50次時，仍未收斂到最優(yōu)解。整個計算過程中，方案三表現(xiàn)出良好的穩(wěn)定性，其反演結(jié)果與

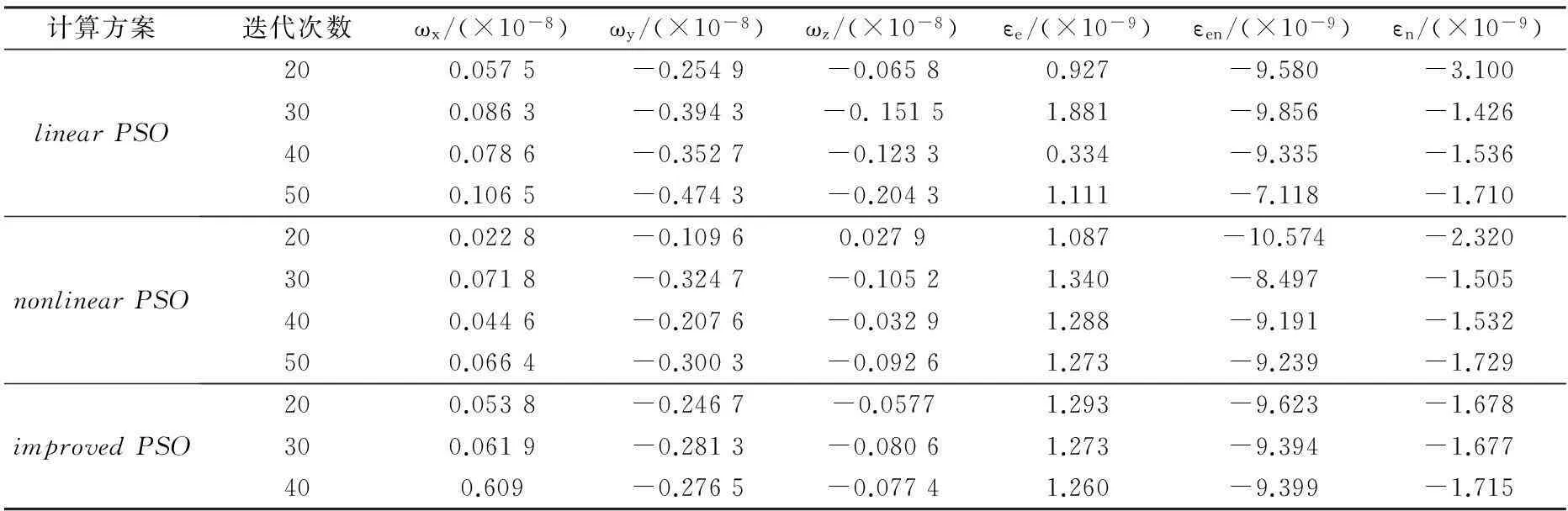
表 2　歐拉和應(yīng)變張量迭代結(jié)果

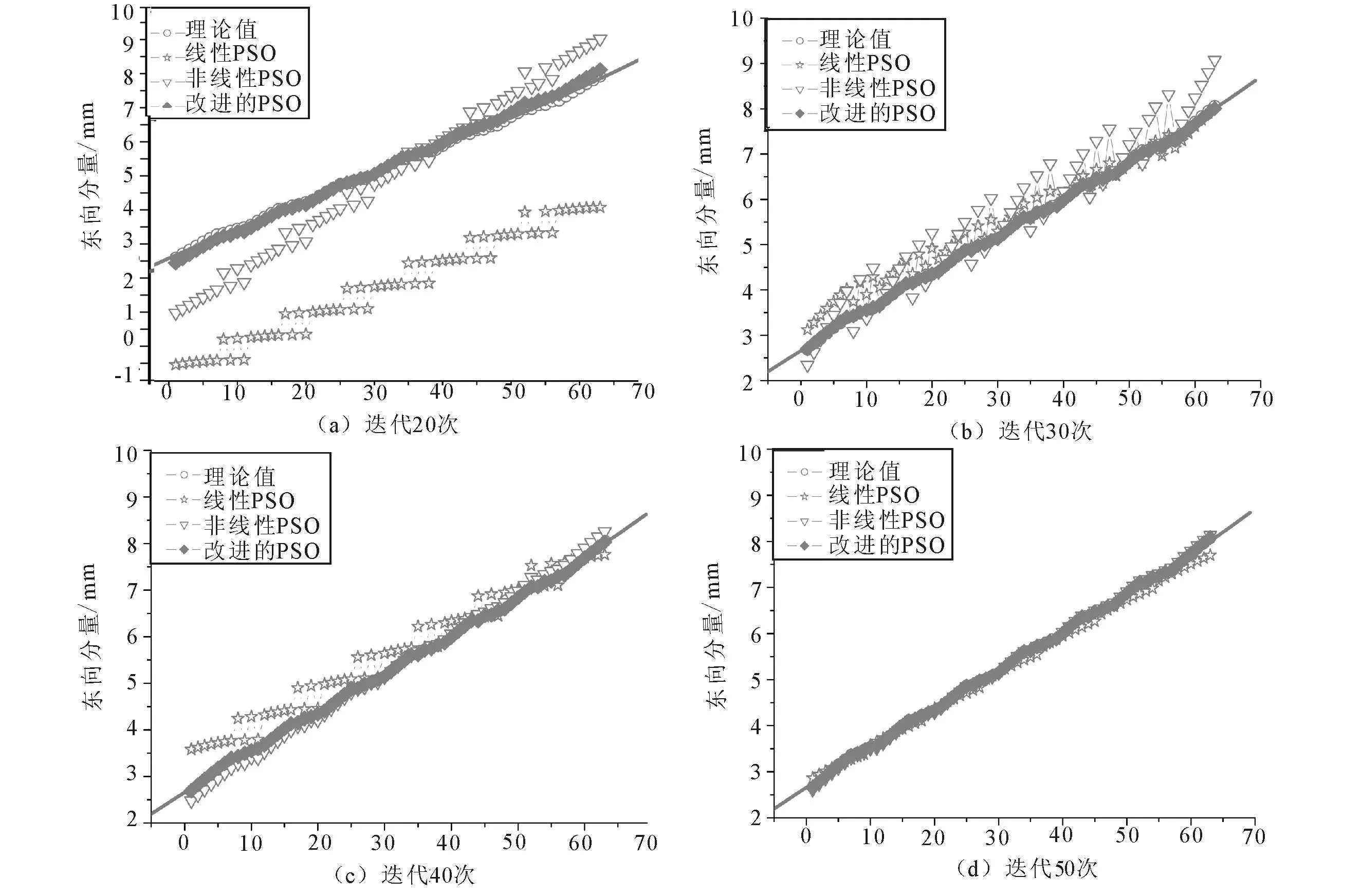
圖1　位移模擬值和理論值(灰色線為理論值擬合曲線) Fig.1　Simulation and theoretical value of the displacements(Gray line is the fitting curve of theoretical value)

Table3Theunbiasednessandeffectivenessofeachalgorithm

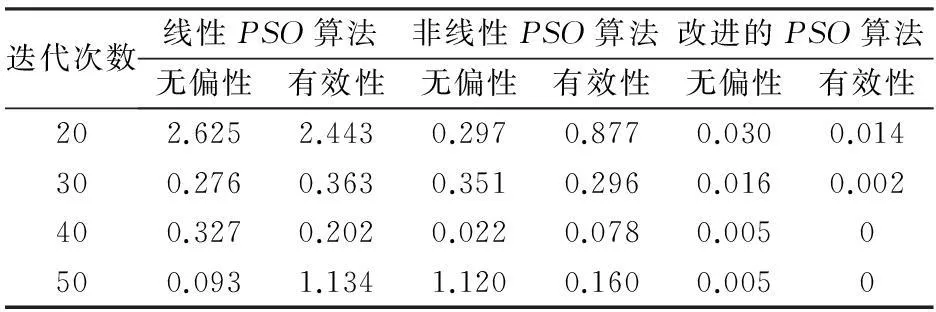
迭代次數(shù)線性PSO算法非線性PSO算法改進的PSO算法無偏性有效性無偏性有效性無偏性有效性202.6252.4430.2970.8770.0300.014300.2760.3630.3510.2960.0160.002400.3270.2020.0220.0780.0050500.0931.1341.1200.1600.0050

理論值具有較好的一致性，20次的迭代結(jié)果已接近最優(yōu)，迭代到50次時，兩者差異(即反演結(jié)果與理論值之差除以理論值，再取絕對值的百分比形式)的最大值( ωz)僅為2.6%。比較算法的無偏性和有效性(表3)可知，改進的PSO算法計算出的位移殘差均值和方差最小，位移場模型的精度最高。綜上可見，維多樣性的動態(tài)權(quán)重粒子群算法反演地殼運動和應(yīng)變張量參數(shù)具有較好的穩(wěn)定性和有效性，且具有一定的抗噪能力，用于構(gòu)建地殼運動速度場模型是可行、適用的。

3青藏高原東北緣速度場模型的建立

3.1GPS資料和塊體運動模型

本文用到的GPS資料為青藏高原東北緣1999—2013年中國地殼運動觀測網(wǎng)絡(luò)觀測到的相對于穩(wěn)定歐亞板塊的水平運動速率結(jié)果[23]。數(shù)據(jù)處理過程如下：首先，用GIPSY/OASIS軟件處理GPS載波相位數(shù)據(jù)，計算站坐標和衛(wèi)星軌道單日松弛解；其次，采用QOCA軟件平差獲得站位置和速度序列；最后，將得到的全球參考框架ITFF2000下的測站速度轉(zhuǎn)換成相對于穩(wěn)定的歐亞板塊的速度場(圖2)。數(shù)據(jù)處理過程中考慮了同震擾動的影響，對同震位移模擬值大于或等于3mm的測站，通過增加同震位移3參數(shù)[1]進行約束求解速度場。

在印度板塊北東向推擠和區(qū)內(nèi)活動斷裂帶的共同作用下，青藏高原東北緣各活動塊體較完整并有相對統(tǒng)一的運動方式，在塊體合理劃分的基礎(chǔ)上，可用歐拉矢量方程(ModelA)、均勻應(yīng)變模型(ModelB)和線性滑動彈塑性模型(ModelC)[22]描述各塊體內(nèi)部的構(gòu)造運動。本文利用瞿偉等[24]對青藏高原東北緣活動塊體的劃分結(jié)果(圖2)，根據(jù)擇優(yōu)的運動模型分別估計各塊體的歐拉和應(yīng)變張量參數(shù)。

3.2改進的粒子群算法建立速度場模型

依據(jù)模型的無偏性和有效性[25]擇優(yōu)標準對各塊體運動模型進行辨識。張輝等[26]通過分析快剪切波平均偏振方向得出青藏高原東北緣區(qū)域應(yīng)力場呈現(xiàn)局部性的特征；明鋒等[27]指出該區(qū)域內(nèi)部變形需引入二階應(yīng)變參數(shù)。因此，各塊體運動模型辨識時，除阿拉善和鄂爾多斯塊體外，其它塊體直接進行均勻應(yīng)變模型(ModelB)和線性滑動彈塑性模型(ModelC)的辨識，結(jié)果如表4所示。然后，根據(jù)反演得到的各塊體歐拉和應(yīng)變張量參數(shù)(表4和表5)，計算了青藏高原東北緣GPS水平運動速率(圖2)。

從圖2可以看出，模擬值與觀測值具有較好的一致性。青藏高原東北緣差異性運動顯著，從南到北水平速率不斷減小，呈順時針旋轉(zhuǎn)運動。區(qū)內(nèi)地殼縮短明顯，青藏高原東北緣NE向運動受到相對穩(wěn)定的阿拉善塊體的阻擋造就了該區(qū)域山體的隆升，盆地的塌陷；鹿化煜等[28]對該區(qū)域代表性的河流階地——風成堆積序列的研究結(jié)果表明，青藏高原東北緣階段性隆升由來已久，且晚新生代處于加速隆升的階段。

圖2　青藏高原東北緣1999—2013年GPS水平運動速率(白色為實測值，黑色為模擬值，單位：mm/a) Fig.2　Horizontal motion rates of GPS in the northeastern margin of the Tibetan Plateau from 1999 to 2013(White arrow denotes observation value，black arrow represents simulation value. unit：mm/a)

表 4青藏高原東北緣各塊體運動模型辨識結(jié)果及相應(yīng)的歐拉矢量參數(shù)(單位：rad/a)

Table4IdentificationresultsofeachblockmotionmodelanditsEulerparametersinthenortheasternmarginoftheTibetanPlateau(unit：rad/a)

塊體名稱ωx/(×10-8)ωy/(×10-8)ωz/(×10-8)無偏性有效性ModelAModelBModelCModelAModelBModelC塔里木0.053-0.175-0.1250.19490.03570.58780.2855阿拉善-0.016-0.0300.0210.66990.02830.47662.42461.15962.3757鄂爾多斯-0.1090.1930.2490.05560.06680.12181.77011.79841.1848祁連山0.019-0.0010.0350.94140.04322.07360.2857海原0.025-0.0900.0260.54290.39852.27241.2481甘青0.012-0.2100.0120.25920.26224.19931.8271共和0.028-0.0250.1560.49280.05832.72191.1528柴達木0.059-0.169-0.0040.39310.31034.03103.1480東昆侖0.210-0.833-0.4330.33770.23848.05622.1249青藏-0.0090.1710.3720.23250.407937.35662.6451

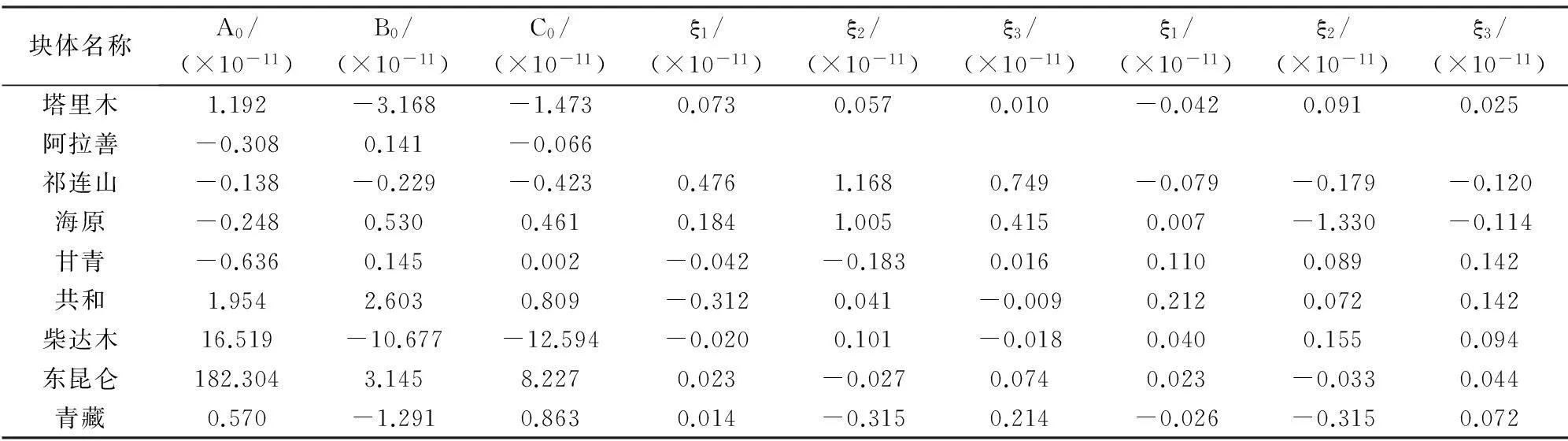
表 5　各塊體應(yīng)變張量結(jié)果

圖3給出了改進的PSO算法計算出的位移殘差分布，可以看出，殘差統(tǒng)計分布基本滿足正態(tài)分布特性，說明構(gòu)建的速度場模型中不含系統(tǒng)誤差。整體上北向分量略優(yōu)于東向分量，可能與本區(qū)域東向分量的復(fù)雜性有關(guān)。與最小二乘配置方法(協(xié)方差函數(shù)取為高斯函數(shù))計算出的位移殘差變化曲線(圖4)比較，可以看出，結(jié)合歐拉矢量的改進粒子群算法構(gòu)建的速度場模型具有較高的精度，再次驗證了本方法建立的速度場模型的可靠性。

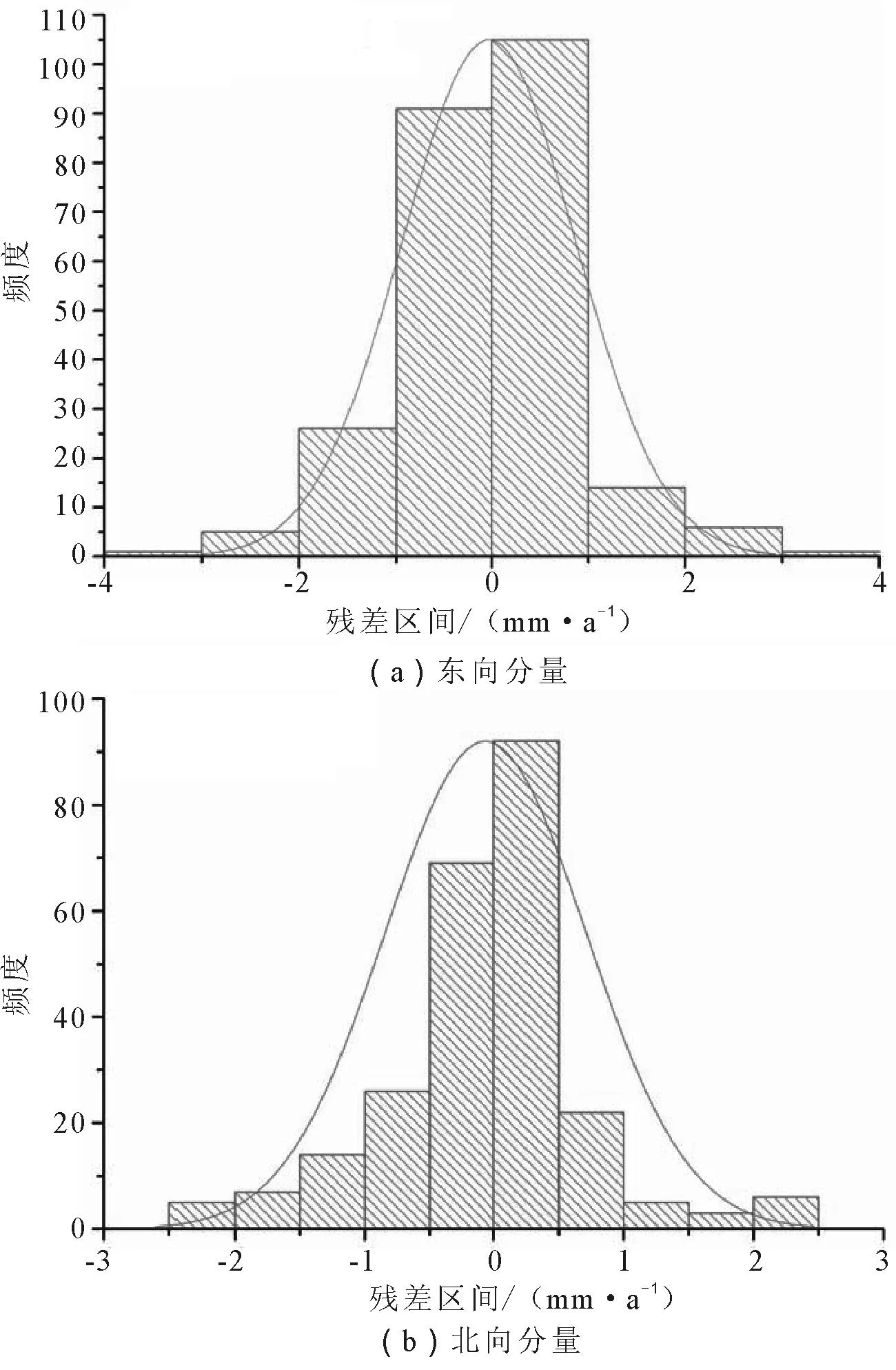
圖3　改進的PSO計算出的位移殘差分布 Fig.3　Residual errov distribution of displacement calculated by improved PSO

圖4　改進的PSO與最小二乘配置法計算出的位移殘差比較 Fig.4　Comparison of residual errors of displacement calculated by improved PSO and LSC

4結(jié)論

目前常用的地殼運動速度場模型的建立方法主要有歐拉矢量法和位移擬合法兩種，不同的建立方法都有一定的前提條件或適用范圍。歐拉矢量法建立的速度場模型具有地學(xué)意義，是在塊體滿足剛性條件下建立的；位移擬合常用的方法有多面函數(shù)法和最小二乘配置法等，多面函數(shù)法中結(jié)點、核函數(shù)的選擇具有很大的不確定性，協(xié)方差函數(shù)決定著最小二乘配置擬合推估的精度，是以隨機信號滿足各態(tài)歷經(jīng)性平穩(wěn)為前提確定的。本文提出利用結(jié)合歐拉矢量的維多樣性動態(tài)權(quán)重粒子群算法構(gòu)建區(qū)域速度場模型，一定程度上克服了速度場模型求解過程中的復(fù)雜程序，可以快速地獲取區(qū)域地殼運動速度場模型，且其精度不低于最小二乘配置法的計算結(jié)果，但仍有不足之處，如對塊體劃分結(jié)果要求較高，若塊體劃分不合理，建立的速度場模型可能會失真，不能反映出真實的地殼形變信息。塊體運動和應(yīng)變張量參數(shù)反演求解時，利用已有成果對解的搜索范圍加以約束效果會更好。

致謝：感謝中國地震局地震預(yù)測研究所武艷強老師在最小二乘配置方面給予的指導(dǎo)。

參考文獻(References)

[1]李強，游新兆，楊少敏，等.中國大陸構(gòu)造變形高精度大密度GPS監(jiān)測——現(xiàn)今速度場[J].中國科學(xué)：D輯，2012，42(5)：629-632.

LI Qiang，YOU Xin-zhao，YANG Shao-min，et al.A Precise Velocity Field of Tectonic Deformation in China as Inferred From Intensive GPS Observations[J].Science China：D Series，2012，42(5)：629-632.(in Chinese)

[2]陳光保.GPS 技術(shù)監(jiān)測地殼運動的新進展[J].西北地震學(xué)報，2009，31(3)：302-307.

CHEN Guang-bao.Recent Progress in Research on Monitoring Crustal Movement and Deformation Using GPS[J].Northwestern Seismological Journal，2009，31(3)：302-307.(in Chinese)

[3]賈鵬，張希，張曉亮，等.汶川地震前后川滇及其鄰區(qū) GPS 水平運動演化特征[J].西北地震學(xué)報，2012，34(3)：264-267.

JIA Peng，ZHANG Xi，ZHANG Xiao-liang，et al.Evolution Features of Crustal Horizontal Movement from GPS Observation in Sichuan—Yunnan Region and Its Adjacent Area Before and After the Wenchuan Earthquake[J].Northwestern Seismological Journal，2012，34(3)：264-267.(in Chinese)

[4]王雙緒，蔣鋒云，李寧，等.岷縣漳縣6.6級地震前區(qū)域地殼運動變形背景與斷層形變異常特征[J].地震工程學(xué)報，2013，35(3)：503-512.

WANG Shuang-xu，JIANG Feng-yun，LI Ning，et al.Regional Crustal Movement Background and Cross-fault Deformation Anomaly Characteristics Prior to the Minxian—ZhangxianMS6.6 Earthquake[J].China Earthquake Engineering Journal，2013，35(3)：503-512.(in chinese)

[5]任金衛(wèi)，馬宗晉.東亞地區(qū)現(xiàn)代地殼運動特征與構(gòu)造變形[J].地學(xué)前緣，2003，10(增刊)：58-65.

REN Jin-wei，MA Zong-jin.Crustal Movement and Tectonic Deformation of Eastern Asia[J].Earth Science Frontiers，2003，10(Supp)：58-65.(in Chinese)

[6]El-Fiky G S，Kato T.Continuous Distribution of the Horizontal Strain in the Tohoku District，Japan，Predicted by Least-Squares Collocation[J].Journal of Geodynamics，1998，27(2)：213-236.

[7]Holt W E，Chamot-Rooke N，Le Pichon X，et al.Velocity Field in Asia Inferred from Quaternary Fault Slip Rates and Global Positioning System Observations[J].Journal of Geophysical Research：Solid Earth (1978—2012)，2000，105(B8)：19185-19209.

[8]王澤民，伍岳，劉經(jīng)南，等.利用 GPS 資料采用非連續(xù)變形分析模型確定中國大陸地殼運動速度場[J].武漢大學(xué)學(xué)報：信息科學(xué)版，2002，27(3)：241-245.

WANG Ze-min，WU Yue，LIU Jing-nan，et al.The Establishment of Crust Motion Velocity Field of China by GPS Observations and Spherical DDA Model[J].Geomatics and Information Science of Wuhan University，2002，27(3)：241-245.(in Chinese)

[9]蔣志浩，張鵬，秘金鐘，等.基于CGCS2000的中國地殼水平運動速度場模型研究[J].測繪學(xué)報，2009，38(6)：471-476.

JIANG Zhi-hao，ZHANG Peng，BI Jin-zhong，et al.The Model of Crustal Horizontal Movement Based on CGCS 2000 Frame[J].Acta Geodaetica et Cartographica Sinica，2009，38(6)：471-476.(in Chinese)

[10]刁法啟，熊熊.地殼運動速度場插值方法研究[J].武漢大學(xué)學(xué)報：信息科學(xué)版，2008，33(6)：627-630.

DIAO Fa-qi，XIONG Xiong.Interpolation Approach for Velocity Field of Crustal Movement[J].Geomatics and Information Science of Wuhan University，2008，33(6)：627-630.(in Chinese)

[11]劉經(jīng)南，施闖，姚宜斌，等.多面函數(shù)擬合法及其在建立中國地殼平面運動速度場模型中的應(yīng)用研究[J].武漢大學(xué)學(xué)報：信息科學(xué)版，2001，26(6)：500-508.

LIU Jing-nan，SHI Chuang，YAO Yi-bin，et al.Hardy Function Interpolation and its Applications to the Establishment of Crustal Movement Speed Field[J].Geomatics and Information Science of Wuhan University，2001，26(6)：500-508.(in Chinese)

[12]石耀霖，朱守彪.用 GPS 位移資料計算應(yīng)變方法的討論[J].大地測量與地球動力學(xué)，2006，26(1)：1-8.

SHI Yao-lin，ZHU Shou-biao.Discussion on Method of Calculating Strain with GPS Displacement Data[J].Journal of Geodesy and Geodynamics，2006，26(1)：1-8.(in Chinese)

[13]Haines A J，Holt W E.A Procedure for Obtaining the Complete Horizontal Motions within Zones of Distributed Deformation from the Inversion of Strain Rate Data[J].Journal of Geophysical Research：Solid Earth (1978—2012)， 1993，98(B7)：12057-12082.

[14]吳云，孫建中，周碩愚.利用地震矩張量反演地殼運動水平速度場的理論和方法[J].大地測量與地球動力學(xué)，1996，16(3)：1-7.

WU Yun，SUN Jian-zhong，ZHOU Shuo-yu.Theory and Method of Inversing Horizontal Velocity Field of Crustal Movement by Seismic Moment Tensor[J].Journal of Geodesy and Geodynamics，1996，16(3)：1-7.(in Chinese)

[15]吳云，帥平，施順英.GPS 觀測量與地震矩張量聯(lián)合反演地殼水平運動速度場的方法[J].大地測量與地球動力學(xué)，1997，17(4)：11-16.

WU Yun，SHUAI Ping，SHI Shun-ying.A Method of Joint Inversion of GPS Observations and Seismic Moment Tensors for Determining Crustal Horizontal Velocity Field[J].Journal of Geodesy and Geodynamics，1997，17(4)：11-16.(in Chinese)

[16]ZHOU Shuo-yu，SHUAI Ping，GUO Feng-ying，et al.A Quantitative Research for Present-time Crustal Motion in Fujian Province, China and its Marginal Sea[J].Acta Seismologica Sinica，2000，13(1)：75-83.

[17]XU Cai-jun，DING Kai-hua，CAI Jian-qing，et al.Methods of Determining Weight Scaling Factors for Geodetic-geophysical Joint Inversion[J].Journal of Geodynamics，2009，47(1)：39-46.

[18]楊維，李歧強.粒子群優(yōu)化算法綜述[J].中國工程科學(xué)，2004，6(5)：87-94.

YANG Wei，LI Qi-qiang.Survey on Particle Swarm Optimization Algorithm[J].Engineering Science，2004，6(5)：87-94.(in Chinese)

[19]王洪濤，任燕.基于改進慣性權(quán)重的粒子群優(yōu)化算法[J].計算機應(yīng)用與軟件，2011，28(10)：271-274.

WANG Hong-tao，REN Yan.Particle Swarm Optimization Algorithm based on Modified Inertia Weight[J].Computer Applications and Software，2011，28(10)：271-274.(in Chinese)

[20]梁昔明，董淑華，龍文，等.動態(tài)慣性權(quán)重向量和維變異的粒子群優(yōu)化算法[J].計算機工程與應(yīng)用，2011，47(5)：29-31.

LIANG Xi-ming，DONG Shu-hua，LONG Wen，et al.PSO Algorithm with Dynamical Inertial Weight Vector and Dimension Mutation[J].Computer Engineering and Applications，2011，47(5)：29-31.(in Chinese)

[21]駱晨鐘，邵惠鶴.采用混沌變異的進化算法[J].控制與決策，2000，15(5)：557-560.

LUO Chen-zhong，SHAO Hui-he.Evolutionary Algorithms with Chaotic Mutations[J].Control and Decision，2000，15(5)：557-560.(in Chinese)

[22]李延興，張靜華，何建坤，等.由空間大地測量得到的太平洋板塊現(xiàn)今構(gòu)造運動與板內(nèi)形變應(yīng)變場[J].地球物理學(xué)報，2007，50(2)：437-447.

LI Yan-xing，ZHANG Jing-hua，HE Jian-kun，et al.Current-day Tectonic Motion and Intraplate Deformation-strain Field Obtained from Space Geodesy in the Pacific Plate[J].Chin J Geophys，2007，50(2)：437-447.(in Chinese)

[23]LIANG Shi-ming，GAN Wei-jun，SHEN Chuan-zheng，et al.Three-dimensional Velocity Field of Present-day Crustal Motion of the Tibetan Plateau Derived from GPS Measurements[J].Journal of Geophysical Research：Solid Earth，2013，118(10)；5722-5732.

[24]瞿偉，張勤，張冬菊，等.基于 GPS 速度場采用 RELSM 模型分析青藏塊體東北緣的形變-應(yīng)變特征[J].地球物理學(xué)進展，2009，24(1)：67-74.

QU Wei，ZHNAG Qin，ZHANG Dong-ju，et al.Analysis of Deformation-strain Characteristics of the Northeast Margin of Qinghai—Tibet Block Using the RELSM Model based on the GPS Velocity Field[J].Progress in Geophys，2009，24(1)：67-74.(in Chinese)

[25]許才軍，溫揚茂.活動地塊運動和應(yīng)變模型辨識[J].大地測量與地球動力學(xué)，2003，23(3)：50-55.

XU Cai-jun，WEN Yang-mao.Identification of Models for Crustal Movement and Strain of Blocks[J].Journal of Geodesy and Geodynamics，2003，23(3)：50-55.(in Chinese)

[26]張輝，高原，石玉濤，等.基于地殼介質(zhì)各向異性分析青藏高原東北緣構(gòu)造應(yīng)力特征[J].地球物理學(xué)報，2012，55(1)：95-104.

ZHANG Hui，GAO Yuan，SHI Yu-tao，et al.Tectonic Stress Analysis based on the Crustal Seismic Anisotropy in the Northeastern Margin of Tibetan Plateau[J].Chin J Geophys，2012， 55(1)：95-104.(in Chinese)

[27]明鋒，柴洪洲.由 GPS 資料討論中國大陸塊體運動與應(yīng)變模型的建立及檢驗[J].地球物理學(xué)報，2009，52(8)：1993-2000.

MING Feng，CHAI Hong-zhou.The Foundation of China Mainland Blocks Movement and Strain Model and its Test based on the GPS Data[J].Chin. J. Geophys，2009，52(8)：1993-2000.(in Chinese)

[28]鹿化煜，安芷生，王曉勇，等. 最近 14 Ma 青藏高原東北緣階段性隆升的地貌證據(jù)[J].中國科學(xué)：D 輯，2004，34(9)：855-864.

LU Hua-yu，AN Zhi-sheng，WANG Xiao-yong，et al.Geomorphologic Evidence of Phased up Lift of the Northeastern Qinghai-Tibet Plateau since 14 Million Years Ago[J].Science in China：Series D，2004，34(9)：855-864.(in Chinese)