基于MATLAB程序實現測量不確定度評定的可行性分析

基于MATLAB程序實現測量不確定度評定的可行性分析

李慧奇1，王凱紅1，張秦2，王永輝2

(1.華北電力大學，河北保定071003；2.國網河北省電力公司電力科學研究院，石家莊050021)

摘要：針對傳統GUM法評定過程繁瑣、計算復雜的問題，提出基于MATLAB程序實現測量不確定度評定的方法，介紹MATLAB程序，分析MATLAB程序在測量不確定度評定過程中的應用步驟及效果，結果表明基于MATLAB程序得到的測量不確定度評定結果與傳統GUM法非常接近，驗證了基于MATLAB程序進行測量不確定度評定的可行性。

關鍵詞：GUM；MATLAB；測量不確定度

收稿日期：2014-10-17

作者簡介：李慧奇(1970—)，男，副教授，主要研究方向為電工理論與新技術。

中圖分類號：TM933

文獻標志碼：B

文章編號：1001-9898(2015)01-0012-03

Abstract：Because the evaluation process of traditional GUM method is complicated and complex, this paper presents the evaluation of Measurement Uncertainty based on MATLAB, introduces the MATLAB program, analyzes MATLAB program procedure and the effect in the process of evaluation of Measurement Uncertainty, the result shows that the result of MATLAB method and GUM method is very close, finally, verifies the feasibility of evaluation of measurement uncertainty based on MATLAB.

Feasibility Analysis on Measurement Uncertainty Evaluation Based on MATLAB

Li Huiqi1,Wang Kaihong1,Zhang Qin2,Wang Yonghui2

(1.North China Electric Power University, Baoding, 071003，China; 2.State Grid Hebei Electric Power Research Institute，Shijiazhuang 050021，China)

Key words：GUM；MATLAB；Measurement Uncertainty

在測量過程中，由于方法、設備、人員、環境等因素的影響，不可避免存在誤差，測量結果具有不確定性。隨著生產的發展和科技的進步，對測量數據的準確性和可靠性提出了更高的要求。不確定度作為評定測量結果質量高低的一個重要指標，顯得極其重要。

測量不確定度是表征合理地賦予被測量之值的分散性，與測量結果相聯系的參數。測量不確定度只說明被測量之值的分散性，而不說明測量結果是否接近真值[1]。測量不確定度的評定前提是：不考慮失誤值，已知的系統影響已修正。GUM法是測量不確定度評定最常用和最基本的方法，應按照國家計量技術規范中的原則、方法和步驟進行評定。文獻[1-3]按照GUM法進行測量不確定度評定，均未進行數據的預處理，而且評定過程比較復雜，數據計算量大。基于MATLAB編程可以實現測量不確定度的評定過程，避免了繁瑣的手工計算，準確性更高，耗費時間更短。

1MATLAB程序介紹

MATLAB是一種用于算法開發、數據可視化、數據分析以及數值計算的高級技術計算語言。MATLAB統計工具箱中有各種隨機數發生器程序，如正態分布、t分布、均勻分布、對數分布等，只需要調用就可以產生大量的隨機數[4]。文獻[5]給出的蒙特卡洛法是一種基于隨機數的計算方法，通過建立一個概率模型或隨機過程，對模型或過程的隨機采樣來計算所求參數的統計特性[6-7]。

2MATLAB程序的應用

2.1　測量數據預處理

由于某種不正常原因造成的粗大誤差是偶爾的，常通過判別而剔除異常數據，格羅布斯準則可靠性高，判別效果較好[1，8-9]。

將測量數據xi按大小順序排列成順序統計量x(i)，即取定顯著度α=0.05，查表可得臨界值g0(n,α)。

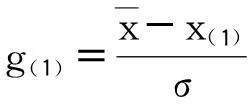
(1)

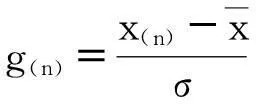
(2)

當g(i)≥g0(n,α)時，即判別該測得值含有粗大誤差，應予剔除。

系統誤差是由于測量設備、方法、原理的不完善、不正確或環境發生變化而引起的，是有規律性的。對于系統誤差的處理應發現它、消除它，并對測量數據予以修正。可用不同公式計算標準差比較法發現系統誤差[1,8]。

(3)

(4)

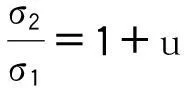
(5)

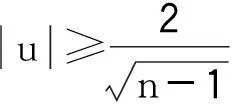
(6)

則懷疑測量列中存在系統誤差。

2.2　GUM法評定測量不確定度

2.2.1測量條件

a. 測量依據：JJG 1052-2009《回路電阻測試儀、直阻儀》[10]。

b. 測量環境條件：溫度為(23±5)℃；相對濕度為40%~75%RH；電壓變化不超過電源額定電壓的±10%。

c. 測量標準器：MJZ-600型模擬大功率交直流標準電阻器，電流測量范圍為1～600 A；交直流電阻測量范圍為0.001 ～60×103mΩ[10]。

d. 被測對象：BZC3395型變壓器直流電阻測試儀，示值誤差為0.2%。

e. 測量過程：采用模擬大功率交直流標準電阻器作為標準設備，用標準電阻法測量變壓器直流電阻測試儀的直流電阻示值誤差。將標準設備和被檢測試儀的電流端、電位端、屏蔽端和接地端分別相連接，根據被檢測試儀電流大小設置好標準設備的量程檔位后開始測試，當被檢測試儀工作電流穩定后，分別記錄標準設備和被檢測試儀的直流電阻值。

2.2.2測量模型

ΔR=Rx-Rn

式中：Rx為變壓器直流電阻測試儀的直流電阻示值；Rn為標準電阻器的直流電阻實際值；ΔR為直流電阻示值的絕對誤差。

2.2.3A類標準不確定度的評定

A類標準不確定度主要是由變壓器直流電阻測試儀測量不重復引起的。根據測量模型，測量結果不確定度來源于Rx變壓器直流電阻測試儀和Rn標準電阻器。

對1臺BZC3395型變壓器直流電阻測試儀100 mΩ點，連續進行10次獨立測量，每次測量均在直流電流為10 A的條件下，得到一組測量數據：99.99，99.99，99.97，99.98，100.0, 99.97，99.97，99.99，100.0，100.0 mΩ。

測量數據的均值為：

(7)

單次實驗標準差：

2.2.3.1判別粗大誤差

從上述測量數據中可知：最大值x(10)=100.0 mΩ；最小值x(1)=99.97 mΩ。查表可得臨界值g0(10, 0.05)=2.18。

若認為x(1)=99.97 mΩ可疑，則有

若認為x(10)=100.0 mΩ可疑，則有

由以上可知：g(1)≤g0(10, 0.05)，g(10)≤g0(10, 0.05)。則可認為該組測量數據不含有粗大誤差。

2.2.3.2判別系統誤差

上述測量數據，按貝塞爾公式可得σ1=σ=0.012 65 mΩ；按別捷爾斯公式可得：

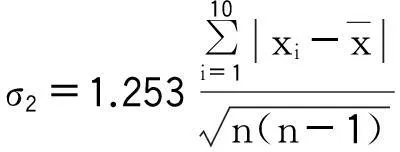
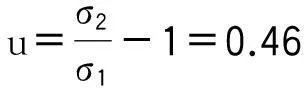
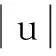
則測量數據中不含有系統誤差。

2.2.3.3計算標準不確定度

測量結果的標準不確定度為:

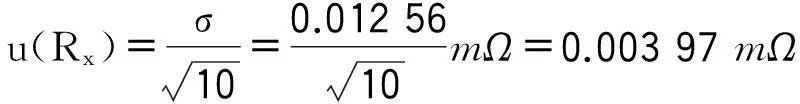
自由度為：v1=n-1=10-1=9

2.2.4B類標準不確定度的評定

標準電阻器Rn的標準不確定度u(Rn)主要由標準電阻器誤差引起的，采用B類評定方法。

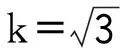
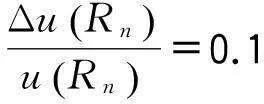
由于說明書中給出標準電阻器的分辨率為0.002μΩ，由分辨率引起的不確定度與標準電阻器誤差引起的不確定度相比可忽略；另外受溫度、濕度變化等其他因素影響的不確定度是極其微小的，也在此忽略[11]。

2.2.5合成標準不確定度的評定

在標準不確定度合成前，將所有通過A類評定和B類評定得到的標準不確定度匯總于表1，以便查看各輸入量標準不確定度的情況[12-14]。

表1標準不確定度匯總表

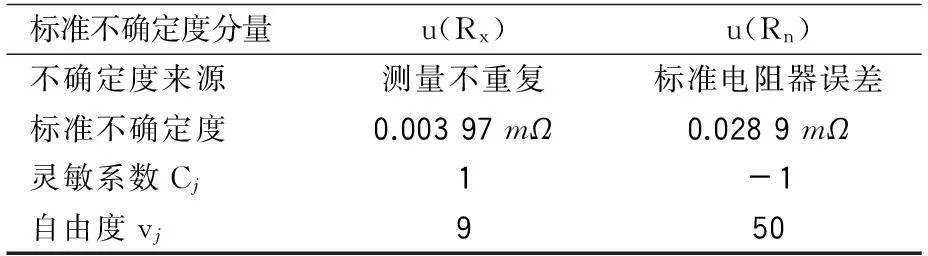
標準不確定度分量u(Rx)u(Rn)不確定度來源測量不重復標準電阻器誤差標準不確定度0.00397mΩ0.0289mΩ靈敏系數Cj1-1自由度vj950

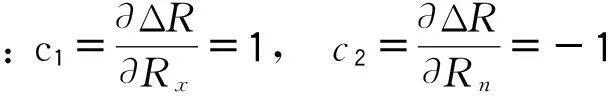
由于變壓器直流電阻測試儀Rx和標準電阻器Rn彼此獨立，合成標準不確定度可按下式得到：

合成標準不確定度的有效自由度為：

2.2.6擴展不確定度的評定

取包含概率p=95%，veff=52，查t分布表并將有效自由度近似取整為50得：

k95=t95(veff)=t95(50)=2.01

擴展不確定度U95為：

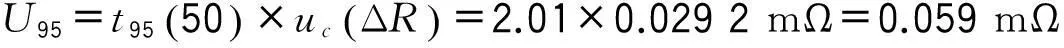
2.3　 MATLAB程序應用效果

MATLAB程序流程示意見圖1。

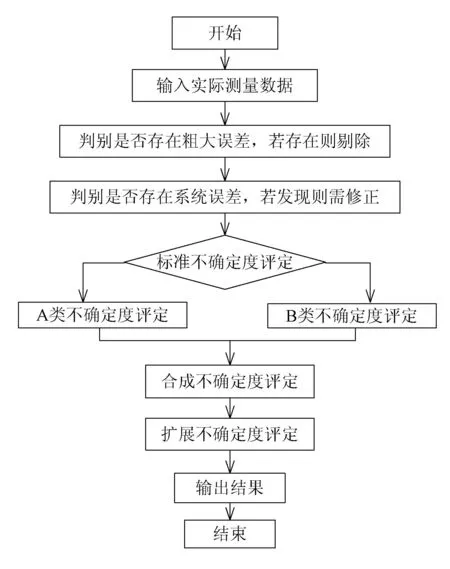
圖1　程序流程示意

將變壓器直流電阻測試儀的測量數據輸入MATLAB程序，運行后結果為：合成不確定度Uc=0.029 1 mΩ，擴展不確定度Up=0.058 6 mΩ。與傳統GUM法計算結果基本一致，驗證了基于MATLAB程序進行測量不確定度評定的可行性。

3結論

a. 基于MATLAB程序實現測量不確定度評定過程，避免了繁瑣的手工計算，準確性更高，耗費時間更短;

b. 運用傳統GUM法進行測量不確定度評定時，往往不注重異常數據的處理問題，建議應首先對數據進行預處理，判別是否存在粗大誤差和系統誤差，然后再進行測量不確定度評定。

參考文獻：

[1]劉瑋蔚.數字式絕緣電阻表測量不確定度的分析與評定[J].河南電力, 2012, 3: 5-6,9.

[2]吳瀛,祁舒喆.電測量變送器檢定裝置測量結果不確定度評定[J].南方電網技術, 2012(6),4:84-86.

[3]孔偉民.用5 520 A建立數字多用表校準裝置測量不確定度評定[J].電子質量, 2013,11:66-70.

[4]林成.工程測量數據誤差及其Matlab處理[J].吉林水利, 2013(10):32-34.

[5]中華人民共和國國家質量檢驗檢疫總局，中國國家標準管理委員會，JJF 1059.2-2012用蒙特卡洛法評定測量不確定度[M].北京：中國計量出版社，2012.

[6]上海市計量測試技術研究院.常用測量不確定度評定方法及應用實例[M].北京:中國計量出版社, 2000.

[7]楊建.蒙特卡羅法評定測量不確定度中相關隨機變量的MATLAB實現[J].計測技術,2012,32(4): 51-54.

[8]趙志剛,趙偉,測量不確定度理論研究和應用中的若干熱點問題[J].電測與儀表,2007,44(3): 1-4.

[9]葛欣宏,賀庚賢,寧飛.防靜電工作區接地電阻的測量不確定度評定[J].電測與儀表, 2013,50(9):46-50.

[10]JJG 1052-2009,回路電阻測試儀、直阻儀[S].

[11]臧景茹.直流數字電壓表法校準電阻箱測量不確定度的評定[J].電測與儀表, 2004(6),41(462):31-33.

[12]JJF 1059—2012,測量不確定度評定與表示[S].

[13]李慎安.關注JJF 1059.1—2012《測量不確定度評定與表示》新規范[J].工業計量,2013,23(3):49-50.

[14]費業泰.誤差理論與數據處理第四版[M].北京:機械工業出版社,2000.

本文責任編輯：楊秀敏