多時變時滯不確定系統的魯棒穩定性

王　坤，王　丹，張　蕊

(燕山大學 理學院，河北 秦皇島 066004)

多時變時滯不確定系統的魯棒穩定性

王坤，王丹，張蕊

(燕山大學 理學院，河北 秦皇島 066004)

摘要：研究了一類不確定多時變時滯系統的魯棒穩定性問題。通過選取適當的Lyapunov函數，利用Jensen不等式和Schur引理，推導出了此類多時變時滯廣義系統漸進穩定的充分條件。最后，通過線性矩陣不等式(LMI)工具箱進行了數值仿真，驗證了該方法的可行性和有效性。

關鍵詞：多時變時滯；不確定性；廣義系統；漸進穩定

基金項目：國家自然科學基金項目(60934003)

作者簡介：王坤(1960-),男,河北秦皇島人,教授,博士,主要從事非線性系統方面的研究.

收稿日期：2014-04-02

文章編號：1672-6871(2015)02-0060-05

中圖分類號：TP273

文獻標志碼：標志碼：A

0引言

不確定性和時滯性在實際系統中是普遍存在的[1-2]，也是導致系統不穩定和性能指標下降的主要原因，所以對不確定時滯系統的研究是非常必要的。廣義系統相對于其他系統更能準確地描述實際動態系統并且廣泛出現在現代工程系統中，因此，近些年對于不確定廣義系統的研究引起了眾多國內外學者的關注[3-6]。文獻[4]針對一類具有范數有界不確定性和多狀態滯后的廣義系統，研究了存在攝動時，系統的非脆弱H∞保性能控制。文獻[7]針對一類李普希茨非線性時滯系統，提出了一種基于線性矩陣不等式設計狀態觀測器的方法。文獻[8]研究了時滯是多個的一類系統的H∞反饋控制問題。文獻[9]考慮了同時具有多重時滯和非線性擾動項時，系統的魯棒預測控制器的設計方法。文獻[10]討論了同時帶有輸入時滯和狀態時滯的線性不確定系統，研究了此類系統在自適應控制器作用下漸進穩定的條件。

本文基于Lyapunov穩定性理論以及已有文獻的研究成果，利用Jensen不等式和Schur引理，分別研究了確定性多時變時滯和不確定多時變時滯廣義系統的魯棒穩定性問題。

1系統描述及引理

考慮下面不確定多時變時滯系統：

(1)

[△A(t)△Ai(t)]=E1F(t)[HHi]，i=1,…,k，

(2)

式中：E1、Hi分別為已知的常矩陣；F(t)為時變的不確定矩陣，滿足FT(t)F(t)≤I。

為簡單起見，記f(t):=f(t,x(t),x(t-τ1(t)),…,x(t-τk(t)))，并且f(t)滿足：

(3)

式中，G為給定的常矩陣。

引理1x和y分別為n維的實列向量，λ為不為0的實數，則有：

2xTy≤λ-1xTx+λyTy。

引理2已知Y為對稱矩陣，D和E是已知的常矩陣，且FTF≤I，則Y+DFE+ETFTDT<0成立的充分必要條件為Y+εDDT+ε-1ETE<0成立，其中ε>0。

(Ⅰ)S<0。

2主要結果

首先研究閉環系統(1)的不確定項△A,△Ai(i=1,…,k)為0，即

(4)

的魯棒漸進穩定性。

定理1對于給定的正數γ>0，若能找到正定矩陣Ri>0(i=1,…,k)和可逆矩陣P有下面的不等式成立：

ETP=PTE≥0；

(5)

(6)

則系統(4)是漸進穩定的。

證明先證系統在無干擾作用下的漸進穩定性。

構造Lyapunov函數：

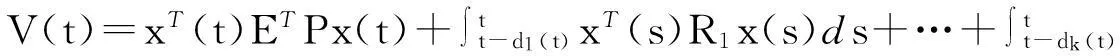
應用Jensen不等式，將Lyapunov函數沿著閉環系統(4)兩端對t求導，得：

(1-η1)xT(t-d1(t))R1x(t-d1(t))+…+

xT(t)Rkx(t)-(1-ηk)xT(t-dk(t))Rkx(t-dk(t))≤

(7)

由引理1可知：

f T(t)Px(t)+xT(t)PTf(t)=2f T(t)Px(t)≤f T(t)f(t)+xT(t)PTPx(t)。

(8)

f T(t)f(t)≤xT(t)GTGx(t)。

(9)

將式(8)和式(9)代入式(7)中，令

其中，ξT(t)=[xT(t) xT(t-d1(t)) … xT(t-dk(t))]。

由矩陣不等式和Schur引理有：

定理1只是給出了當不確定項為0時，系統(1)漸進穩定的充分條件，而這只是一個特殊的情況。對于一般情況(即不確定項不為0時)，應用定理1中的不等式求解會很困難，故下面的定理2給出了定理1的等價結論，并且可以利用線性矩陣不等式(LMI)工具箱求解。

定理2對于多時變時滯廣義系統(1)，如果存在實數εi>0 (i=1,…,k),矩陣Ri>0 (i=1,…,k)和可逆矩陣X，有下面的不等式成立：

ETX-1=X-TE≥0 ;

(10)

(11)

其中：

則系統(1)是漸進穩定的。

證明當不確定項不為0時，用A+△A，Ai+△Ai(i=1,…,k)分別代替式(6)中的A,Ai，經過整理，令

其中：

Ω2=△ATP+PT△A。

所以式(6)可以等價變形為：

Y+Y1<0。

(12)

式(12)可以寫成：

(13)

應用引理2，式(13)等價于下面的不等式：

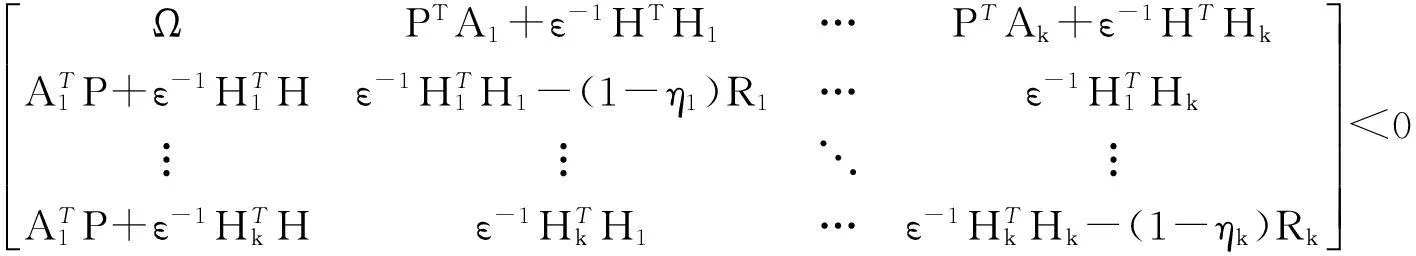
(14)

其中，

利用引理3，式(13)等價于：

(15)

其中,

用矩陣diag[P-TI … I]和矩陣diag[P-1I … I]分別左乘和右乘式(14)，令X=P-1，代入到式(5)中，于是便可以得到式(10)和式(11)，故定理2得證。

3仿真實例

例1考慮多時變時滯系統(4)，以i=1,2為例，設定參數如下:

給定η1=0.8,η2=0.72,根據給定的參數以及定理1，利用LMI工具箱中的Feasp求解器進行求解，可知本文中的線性矩陣不等式是可行的，并且得到一個可行解：

例2考慮多時變時滯系統(1)，以i=1為例，設定參數如下:

給定ε=0.6，η1=0.72，根據給定參數以及定理2，利用Matlab中LMI工具箱求解，得到：

圖1　系統狀態響應圖

數據仿真結果如圖1所示，仿真結果表明所研究的系統是漸進穩定的。

4結束語

本文研究了不確定多時變時滯廣義系統的漸進穩定性問題，通過選取適當的Lyapunov函數，結合Lyapunov穩定性理論，得到了使得此類系統漸進穩定的充分條件；最后利用數值算例及圖形仿真驗證了該方法的有效性。但是，多時變時滯廣義系統的魯棒問題涉及的領域很多，包含的內容很廣，本文在先前發表的研究成果上，增加了多時變時滯項，使得此系統更加具有普遍性。在此后的研究中，可以在本文的基礎上，設計一個適當形式的無記憶狀態反饋控制器，并且通過證明給出控制器的一般形式。

參考文獻：

[1]Li Q,Zhang Q,Yi N,et al.Robust Passive Control for Uncertain Time-delay Singular Systems[J].IEEE Trans Circuits Syst I:Fundam Theory Appl,2009,56(3):653-663.

[2]Jeong S C,Park P G.Constrained MPC Algorithm for Uncertain Time-varying Systems with State-delay[J].IEEE Transactions on Automatic Control,2005,50(2):257-263.

[3]Tang S,Meng B,Gao C.Delay-dependent Robust Passive Control for Discrete Singular Systems with Multiple Time-delays[J].Advanced Materials Research,2012,433:4284-4290.

[4]Zhu S,Zhang C,Cheng Z.Delay-dependent Robust Stability Criteria for Two Classes of Uncertain Singular Time-delay Systems[J].IEE Transactions on Automatic Control,2007,52(5):880-885.

[5]平續斌,丁寶蒼,韓崇昭.動態輸出反饋魯棒模型預測控制[J].自動化學報,2012,38(1):31-37.

[6]楊國詩,何德峰,薛美盛.基于魯棒控制Lyapunov函數的非線性預測控制[J].控制與決策,2010,25(11):1752-1756.

[7]蔣建虎,宋麗君,宋書中.一類不確定非線性時滯系統的觀測器設計[J].河南科技大學學報:自然科學版,2012,33(1):32-36.

[8]陳嶠郴,邵克勇.多時滯不確定系統的H∞反饋控制[J].控制理論與應用,2013,32(4):6-9.

[9]蘇成立,趙家程,李平.一類具有非線性擾動的多重時滯不確定系統魯棒預測控制[J].自動化學報,2013,39(5):644-649.

[10]候曉麗,邵誠.具有輸入時滯的不確定系統魯棒自適應控制[J].河南科技大學學報:自然科學版,2013,34(4):57-60.