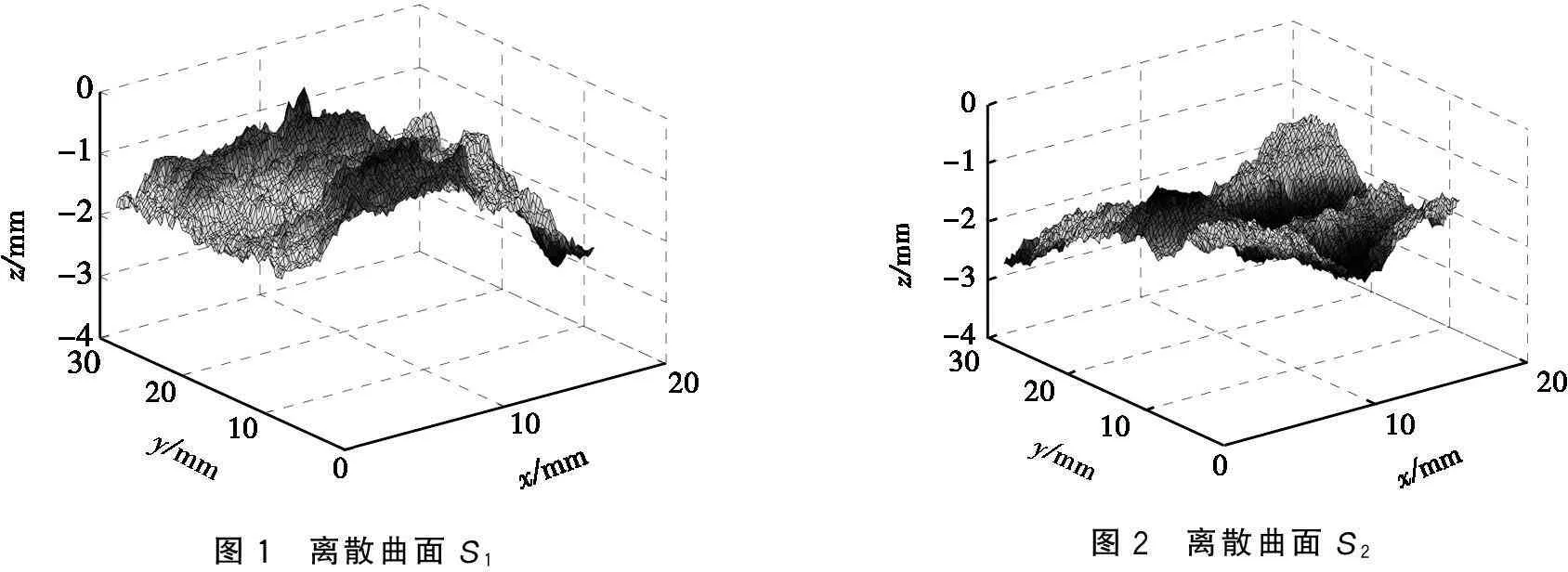
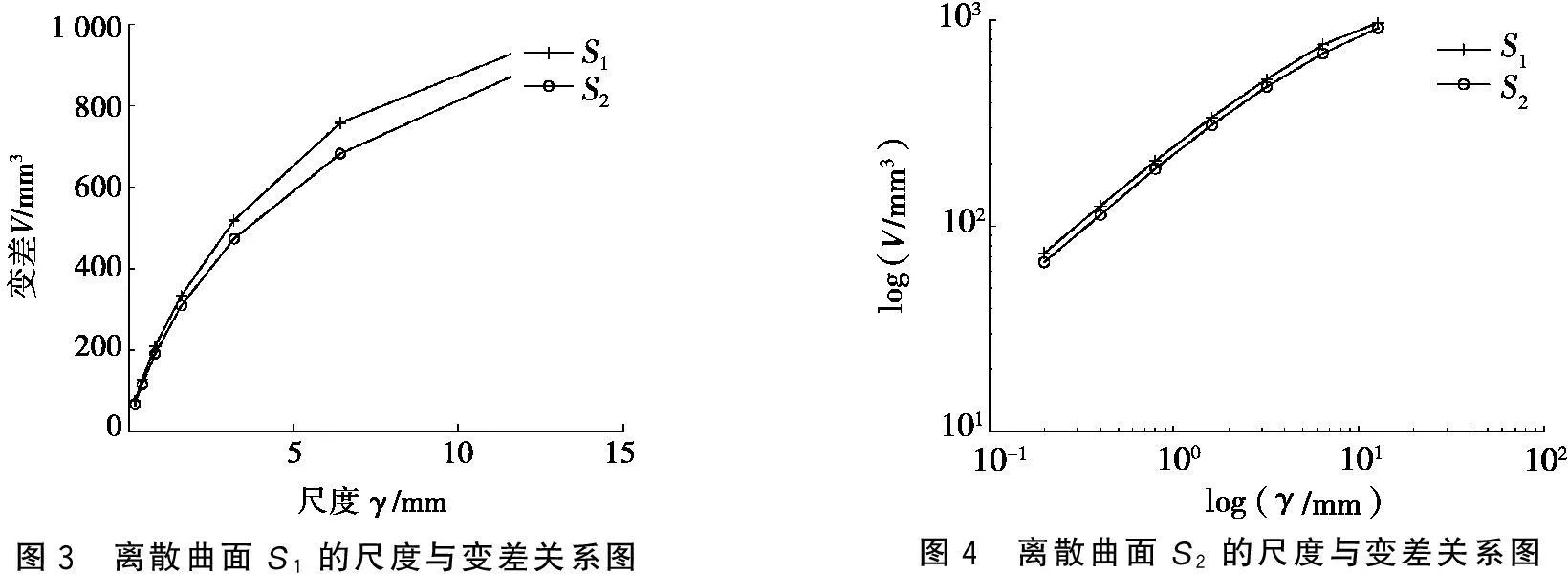
離散曲面變差的計算

郭艷芳，馮志剛

(江蘇大學 理學院，江蘇 鎮江 212013)

離散曲面變差的計算

郭艷芳，馮志剛

(江蘇大學 理學院，江蘇 鎮江 212013)

摘要：在連續函數變差相關理論基礎上，為了更好地描繪實驗或實際測得的曲面數據，本文引入離散曲面變差的概念，并提出了離散曲面變差的計算方法。針對兩組不同的離散曲面數據,計算它們在不同尺度下的變差以及尺度和變差的雙對數圖，比較了兩組離散曲面的維數與變差關系。研究結果表明：本文提出的離散曲面變差的計算方法是可行的，可以作為計算離散曲面變差的一種方法。

關鍵詞：二元連續函數;離散曲面;振幅;變差

基金項目：國家自然科學基金項目(51079064)

作者簡介：郭艷芳(1988-),女,山西呂梁人,碩士生;馮志剛(1962-),男,江蘇常州人,教授,碩士生導師,主要從事分形幾何理論的研究.

收稿日期：2014-07-04

文章編號：1672-6871(2015)02-0088-04

中圖分類號：O244

文獻標志碼：志碼：A

0引言

變差[1-4]作為刻畫曲面粗糙度的一種重要參數，可以用來研究各種尺度下函數的粗糙度，而粗糙度在材料學、力學等學科中有著非常廣泛的應用。研究自然界中各種材料、巖石、零件間的裂紋、斷裂面的粗糙度，對研究裂紋的萌發、擴展以及最后導致材料斷裂破壞這一整個過程的本質規律起著十分重要的作用。大量的研究已經證實斷層、裂隙和節理的粗糙度，在采礦工程和土木工程中經常發生的滑坡及冒頂這些災害性事故的發生中起著十分重要的作用。

文獻[5]給出了連續函數的變差概念，對于連續函數f：I→，設δ>0，t∈I，稱

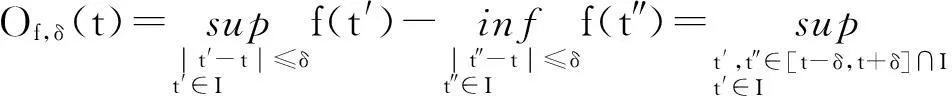
為f基于I在點t的δ-振幅，稱Vf,δ(I)=∫IOf,δ(t)dt為函數f在I上的δ-變差。

文獻[5]還研究了連續函數的δ-變差的性質，并給出二維平面上連續函數圖像的計盒維數的計算公式，即設f:I→為連續函數，Γ(f,I)為f在I上的圖像，則

文獻[6]定義了三維空間中曲線的變差。而文獻[7]在變差的基礎上給出了三維空間中函數圖像的計盒維數的公式。文獻[8-9]介紹了二元連續函數的振幅和變差。對于在D上連續的函數y=f(x,y)，設I=[a,b],J=[c,d]是的子集，D=I×J是2上的區域，δ、γ是非負實數；對任何(x,y)∈D,函數f(x,y)在點(x,y)∈D的(δ,γ)-振幅，記為(x,y)，簡記為Of;δ,γ(x,y)。且

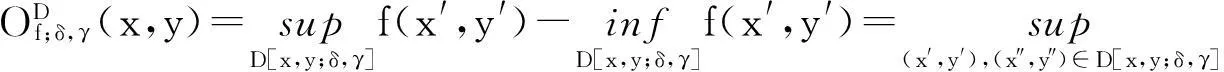
其中，D[x,y;δ,γ]=D∩([x-δ,x+δ]×[y-γ,y+γ])。函數f在區域D上的(δ,γ)-變差，記為Vf;δ,γ(x,y)，且

Vf;δ,γ(x,y)=?DOf;δ,γ(x,y)dxdy，

并證明了變差的一些性質，通過連續函數圖像的計盒維數和它的變差之間的聯系，得出了分形插值曲面的計盒維數公式[7-13]:

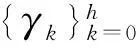
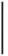
(1)

其中，G((xi,yj),γk)=([xi-γk,xi+γk]×[yj-γk,yj+γk])∩G。

離散曲面S:{(xi,yj,zij):i=1,2,…,m;j=1,2,…,n}的γk-變差為Vs(γk)，且

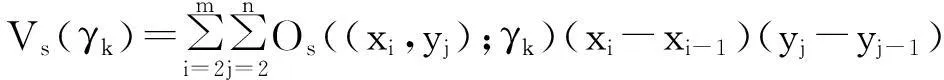
(2)

接著給出了離散曲面變差的計算方法，該方法在求尺度較大的離散曲面的變差時，有著明顯的優勢。例如：求離散曲面S中點(xi,yj)的γk-振幅，只需比較(xi-γk-1,yj-γk-1)，(xi-γk-1,yj+γk-1)，(xi+γk-1,yj-γk-1)，(xi+γk-1,yj+γk-1)4點的最大值、最小值，不需要通過比較[xi-γk,xi+γk]×[yj-γk,yj+γk]中每一點的最大值、最小值求出每一點在尺度γk下的振幅，進而求出在尺度γk下的變差。

1離散曲面的變差計算

本文只討論當曲面數據等距時，離散曲面的變差計算。

當曲面數據等距時，即xi-xi-1=yj-yj-1=ρ(常數)，i=2,3,…,m;j=2,3,…,n。由曲面數據的離散特征，離散曲面的尺度γk可以取ρ的整數倍，特別地，可以取2進制的倍數γk=2kρ。其中，k∈Z，且0≤k≤log2max{m-1,n-1}。

下面研究γk=2kρ時離散曲面的變差算法，其中，0<γk≤max{xm-x0,yn-y0}。

由于式(1)也可表示為:

Os((xi,yj);γk)=max{zl,p:(xl,yp)∈G((xi,yj),γk)}-min{zl,p:(xl,yp)∈G((xi,yj),γk)},

所以對于i=0,1,2,…,m,m+1;j=0,1,2,…,n,n+1,計算

(3)

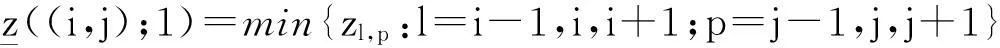
(4)

對于i=-2k+1,-2k+2,…,-2k+m;j=-2k+1,-2k+2,…,-2k+n，計算

(5)

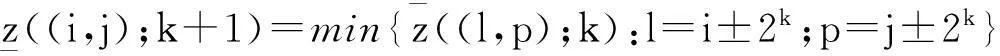
(6)

得到離散曲面S在(xi,yj)的γk-振幅為：

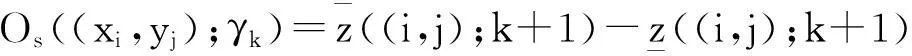
(7)

再計算曲面S的γk-變差：

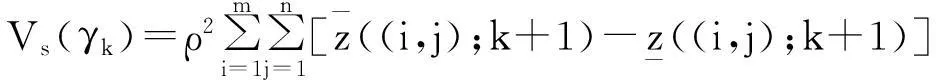
(8)

特別地，如果上述公式中的指標(l,p)超出前面計算出的范圍，則不計在內。為了在計算機操作過程中解決這一問題，本文給出的算法程序中，針對已經給出的曲面數據擴充得到足夠大的矩陣，從而解決了在式(3)~式(6)中指標(l,p)超出范圍的問題。

由式(3)~式(8)，本文設計了一個算法程序，其基本步驟如下：

步驟1把矩陣z=(zij)m×n擴充成一個新的矩陣B=(Bij)(2k+1+m)×(2k+1+n),

當1≤i≤2k+1且 1≤j≤2k+1時，B(i,j)=z(1,1);

2k+1

2k+n≤j≤2k+1+n時，B(i,j)=z(1,n)。

當2k+1

2k+1

2k+n≤j≤2k+1+n時，B(i,j)=z(i-2k,n)。

當2k+n≤j≤2k+1+n且1≤j≤2k+1時，B(i,j)=z(m,1);

2k+1

2k+n≤j≤2k+1+n時，B(i,j)=z(m,n)。

步驟2求矩陣B(i,j)在尺度γ=20·ρ下的最大值BM1(i,j)，最小值Bm1(i,j)，即

BM1(i,j)=max{B(i-1,j-1)，B(i-1,j),B(i-1,j+1),B(i,j-1),B(i,j),

B(i,j+1)，B(i+1,j-1),B(i+1,j),B(i+1,j+1)}；

Bm1(i,j)=min{B(i-1,j-1)，B(i-1,j),B(i-1,j+1),B(i,j-1),B(i,j),

B(i,j+1),B(i+1,j-1),B(i+1,j),B(i+1,j+1)}，

其中：2≤i≤2k+1+m-1；2≤j≤2k+1+n-1。

步驟3求矩陣B(i,j)在尺度γ=2t·ρ，1≤t≤k下的最大值BM1(i,j,t)，最小值Bm1(i,j,t)，其中，1+2t≤i≤2k+1+m-2t,1+2t≤j≤2k+1+n-2t,且

BM1(i,j,t)=max{BM1(i-2t,j-2t,t-1),BM1(i-2t,j+2t,t-1)，

BM1(i+2t,j-2t,t-1)，BM1(i+2t,j+2t,t-1)};

Bm1(i,j,t)=min{Bm1(i-2t,j-2t,t-1),Bm1(i-2t,j+2t,t-1)，

Bm1(i+2t,j-2t,t-1),Bm1(i+2t,j+2t,t-1)}。

步驟4求B(i,j)在尺度γ=2k·ρ下的振幅Os(i,j)=BM1(i,j)-Bm1(i,j)，其中2k+1≤i≤2k+1+m,2k+1≤j≤2k+1+n，則z(i,j)在尺度γ=2k·ρ下的變差為

Vs=ρ2·∑∑Os(i,j)。

2舉例

給出離散曲面S1、S2，如圖1和圖2所示。

x1=0, x100=19.800, y1=8.212, y100=28.012, xi-xi-1=yj-yj-1=0.200,

其中：i=2,3，…100;j=2,3,…，100；xi、yj、zij的單位均為mm。

圖1 離散曲面S1圖2 離散曲面S2

計算得出兩個離散曲面在不同尺度下的變差值，如表1所示。離散曲面S1、S2的尺度γ與變差V的關系圖以及γ與V的雙對數圖，如圖3和圖4所示。

表1　離散曲面S1、S2在不同尺度下的變差值

圖3 離散曲面S1的尺度與變差關系圖圖4 離散曲面S2的尺度與變差關系圖

由圖3可知：變差是反映曲面粗糙程度的重要參數。當尺度γ較小時，離散曲面S1、S2的變差很接近；隨著尺度γ不斷增大，離散曲面S1的變差較離散曲面S2的變差增幅大；且當尺度足夠大以后，離散曲面S1的變差明顯比離散曲面S2的變差大，離散曲面S1比離散曲面S2表現的粗糙，這與圖1和圖2是相符的。

圖4表示log(Vs(γk)-log(λk))的雙對數圖像，與圖3的變化規律是一致的。由曲面變差與計盒維數之間的關系，可以得出：離散曲面S1和S2的平均計盒維數分別為2.37和2.36，即離散曲面S1比離散曲面S2粗糙一些，這與已經得出的結果一致。

3結論

本文在連續函數變差的基礎上，提出離散曲面變差的計算；并針對于等距的離散曲面數據，給出了離散曲面的變差計算方法；最后通過兩個實例的結果驗證了該方法的可行性以及正確性。

參考文獻：

[1]Tricot C.Curves and Fractal Dimension[M].New York:Spinger-Verlag New York Inc,1995.

[2]Dubuc B,Tricot C.Variation d’une Function et Dimension de son Graph[J].Math Acad Sci Paris Ser:I,1988,306:531-533.

[3]Tticot C.Funtion Norms and Fractal Dimension[J].SIAM J Math Anal,1997,28(1):189-212.

[4]Dubuc B,Zucker S W,Tricot C,et al.Evaluating the Fractal Dimension of Surfaces[J].Proc R Soc Lond Ser:A,1989,425:113-127.

[5]文志英.分形幾何的數學基礎[M].上海:上海科學技術出版社,2000.

[6]馮志剛,王磊.分形差值函數的變差的性質[J].江蘇大學學報:自然科學版,2005,26(1):49-52.

[7]李玲，馮志剛，許榮飛.三維空間中函數圖像的計盒維數[J].安徽工業大學學報，2007，24(1)：113-116.

[8]Feng Z G.Variation and Minkowski Dimension of Fractal Interpolation Surface[J].J Math Anal Appl,2008,345(1):322-334.

[9]徐惠,馮志剛.一類分形插值函數的變差和計盒維數[J].安徽工業大學學報,2008,25(4):444-447．

[10]黃艷麗,馮志剛.基于二次分形插值函數的分形插值曲面的變差與盒維數[J].河南科技大學學報:自然科學版,2011,32(3):68-71.

[11]黃艷麗,馮志剛.基于分形插值函數的分形插值曲面的變差與計盒維數[J].工程數學學報,2012,29(3):393-398.

[12]Feng Z G,Sun X Q.Box-counting Dimensions of Fractal Interpolation Surfaces Derived from Fractal Interploation Functions[J].J Math Anal Appl,2014,412(1):416-425.

[13]毛北行,孟金濤.離散復雜網絡系統的混沌同步[J].鄭州大學學報:理學版,2013,45(3):9-12.