一般函數的計算機病毒模型最優控制

孫德順，蘇永美

(北京科技大學 數理學院,北京 100083)

一般函數的計算機病毒模型最優控制

孫德順，蘇永美

(北京科技大學 數理學院,北京 100083)

摘要：研究一類改進的一般函數的計算機病毒模型，并引入殺毒軟件作為系統的控制變量，應用極小值原理，得到一個時變的最優控制策略。時變的控制策略不但能夠使得購買殺毒軟件及其更新的費用最小,而且能將被感染的計算機的數目降到最低。數值模擬顯示：在控制的這段時間內，并不需要一直保持最大的效力。

關鍵詞：計算機病毒;一般函數;最優控制;數值模擬

基金項目：國家自然科學基金項目(61074192,11101028)

作者簡介：孫德順(1990-),男,山東臨沂人,碩士生;蘇永美(1971-),女,山東臨沂人,副教授,博士,碩士生導師,主要從事常微分方程定性與穩定性分析,生物數學模型、計算機模型的最優控制方面的研究.

收稿日期：2014-09-05

文章編號：1672-6871(2015)02-0096-04

中圖分類號：O175.12

文獻標志碼：志碼：A

0引言

計算機病毒通過各種渠道，從已被感染的計算機擴散到未被感染的計算機,其破壞性及傳染性對社會造成極大的傷害，僅2008年，計算機病毒在全球造成的經濟損失就高達85億美元。考慮到計算機病毒和生物學病毒[1-3]有很高的相似性，相應的計算機病毒模型[4-8]被提出，通過研究其動力學特性，從而找到能有效控制病毒在網絡中傳播的方法。

自極小值原理被提出以來，最優控制理論得到了極大的發展，在控制生物學病毒的傳播上得到了廣泛的應用，但是在計算機病毒最優控制方面卻研究的很少。文獻[9-10]利用控制理論研究計算機病毒模型，但都是基于雙線性函數和具體函數的研究。本文利用最優控制理論的方法，在文獻[11]提出的模型基礎上進行研究。通過引入控制變量，提出目標函數，轉化為最優控制的問題，并以數值模擬驗證其正確性。

1模型

所有計算機分為易感染病毒計算機S，已感染病毒計算機I,獲得暫時性免疫計算機R。本文根據文獻[11]，提出帶有控制的計算機病毒模型如下:

(1)

在文獻[11]中,p為免疫率;b為入網率;考慮到殺毒軟件的存在，每臺易感染病毒計算機S都獲得暫時性免疫，此時的免疫率為α1;μ為斷網率;γ為暫時性免疫計算機R重新成為易感染病毒計算機的比率;γ2為已感染病毒計算機成為易感染病毒計算的殺毒率;α為已感染病毒計算機獲得免疫的免疫率;由于已感染病毒計算機的侵入，t時刻每臺易感染病毒計算機S的感染率為βI/f(I)。文獻[11]中的字母表示和本文模型中字母具有相同的意義。但是在實際情況中，用戶可以通過操作殺毒軟件來控制感染病毒的計算機數目，而文獻[11]中殺毒率γ2和α是常數，不能很好地反映人為操作殺毒軟件的作用。因此，本文在文獻[11]的基礎上進行改進，將常數γ2和α改成控制變量函數ωu(t)和(1-ω)u(t)，這里u(t)代表殺毒率。根據文獻[12]，標準發生率更加符合實際情況，所以本文將一般發生率f(I)改為f(S,I)。

2最優控制問題

根據龐德里亞金的極小值原理，需要在系統 (1)上建立一個最優控制系統來控制病毒的傳播。為了建立最優控制系統，對于給定的整數T>0，選擇下面的集合作為控制集：

U={u(t)∈L2(0,T):0≤u(t)≤1,0≤t≤T}，

(2)

其中，控制變量u(t)可以通過更新殺毒軟件，將感染病毒的計算機數目降低到一個較低水平甚至幾乎為0。

目標泛函定義為：

(3)

其中：t0為控制的起始時刻;tf為控制的終點時刻;S11、R11、Q11表示對應變量的權重。給定初始條件為：

S(t0)=S0,I(t0)=I0,R(t0)=R0。

(4)

選取上述的目標函數J(u(t))是為了既能保證將受感染的計算機的數量控制到最低水平，同時也可以保證為此而購買的殺毒軟件和軟件的更新費用最少。

為了找到目標泛函的最小值，定義Hamiltonian函數[13]如下：

(5)

最優控制的存在性證明。由文獻[14]，且方程(1)~方程(3)滿足如下條件：

(Ⅰ)控制集和相對應的狀態變量集為非空集合。

(Ⅱ)可測集U是閉的凸集。

(Ⅲ)系統(1)方程的右邊關于u的線性函數，并且是連續有界的。

(Ⅳ)目標泛函的被積函數L(I,u)在U上是凹函數。

綜上所述，系統(1)存在最優控制。

利用龐德里亞金的極小值原理求出最優控制的必要條件如下[13]：

(Ⅱ)斜狀態方程：

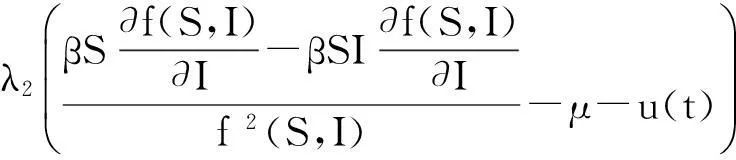
(Ⅲ)橫截條件：λi(T)=0，i=1，2，3。

(Ⅳ)邊界條件：S(t0)=S0,I(t0)=I0,R(t0)=R0。

因為假定控制的范圍是0≤u(t)≤1，本文得到最優控制變量如下：

3數值模擬

根據前面的理論分析，通過數值模擬來驗證使用適當的控制策略之后，計算機病毒傳播將得到有效控制。此外，將殺毒率分別是常數和變量函數進行比較，通過數值模擬得到：時變的最優控制模型能夠更加有效地抑制計算機的感染和病毒的傳播。

數值模擬選取如下參數：p=0.1，b=5，α1=0.1，μ=0.003，β=0.038，γ=0.6，γ1=0.01，γ2=0.003，ω=0.5;初值選取：S(0)=800，I(0)=200，R(0)=50。 控制的時間t0=0，tf=100，S11=0，Q11=1 000，R11=5 000。

圖1為在有無控制條件下，未感染、易感染和免疫的計算機數量的變化趨勢和控制量。

圖1　在有無控制條件下，未感染、易感染和免疫的計算機數量的變化趨勢以及控制量

由圖1可看出：在經過如圖1d的控制量的條件下，計算機病毒的蔓延和傳播得到了有效的控制。通過圖1a可明顯看到：在沒有有效控制的條件下，易感染的計算機數量是明顯下降的，甚至接近600，而在經過控制的條件下，易感染計算機的數量(也就是健康的計算機數量)是逐漸增加的。圖1b中顯示的是被感染的計算機的數量，同樣的，在沒有控制的條件下，感染的計算機數量幾乎呈直線上升，如果是這樣，造成的后果將不可估量。加入了控制，也就是殺毒軟件，在前5天被感染的計算機數量就降下來了。同樣對于圖1c，在加入控制之后的免疫的計算機較以往也是有所提升。圖1d表示最優控制量的變化趨勢。通過圖1d可以看到：在控制的前42天需要保持控制的最大效力，從第42天到第55天，控制逐漸降到極小值;而再從第55天到第100天，控制的效力維持在0.15，也就是說只需維持一個低的效力就能保證計算機都是健康的。

4結論

在有最優控制條件下，易感染的計算機的數量和被感染的計算機的數量趨勢是符合目標函數的預期，而在沒有控制的條件下，計算機病毒的傳播無法被控制。從控制量的走勢也可以明顯看到：并不需要一直持續的最大效力，就可以將計算機病毒的傳播控制住。這也是符合最優控制的目標：在費用最小的前提下，被感染的計算機的數量最少。

參考文獻：

[1]Wierman J C,Marchette D J.Modeling Computer Virus Prevalence with a Susceptible Infected Susceptible Model with Reintroduction[J].Computational Statistics & Analysis，2004,45(1):3-23.

[2]Yuan H,Chen G.Network Virus Epidemic Model with the Point to Group Information Propagation[J].Applied Mathematics and Computation,2008,206(1):357-367.

[3]Mishra B K,Saini D K.SEIRS Epidemic Model with Delay for Transmission of Malicious Objects in Computer Network[J].Applied Mathematics and Computation,2007,188(2):1476-1482.

[4]Billings L,Spears W M,Schwartz I B.A Unified Prediction of Computer Virus Spread in Connected Networks[J].Physics Letters A,2002,297(6):261-266.

[5]Piqueira J R C,Navarro B F.Epidemiological Models Applied to Viruses in Computer Networks[J].Joumal of Computer Science,2005(1):31-34.

[6]Gan C Q,Yang X F,Liu W P,et al.A Propagation Model of Computer Virus with Nonlinear Vaccination Probability[J].Commun Nonlinear Sci Numer Simulat,2014,19:92-100.

[7]Mishra B K,Pandey S K.Dynamic Model of Worms with Vertical Transmission in Computer Network[J].Applied Mathematics and Computation,2011,217:8438-8446.

[8]王娟;何俊杰;王倩.一類具有時滯的媒介傳染病模型非負解的存在性[J].鄭州大學學報:理學版,2014,46(3):1-4.

[9]張旭龍,楊小帆.計算機病毒的最優控制模型[J].計算機應用研究,2011,28(8):3040-3042.

[10]Zhu Q Y,Yang X F,Yang L X,et al.Optimal Control of Computer Virus Under a Delay Model[J].Applied Mathematics and Computation,2012,218:11613-11619.

[11]Gan C Q,Yang X F,Liu W P,et al.An Epidemic Model of Computer Viruses with Vaccination and Generalized Nonlinear Incidence Rate[J].Applied Mathematics and Computation,2013,222:265-274.

[12]Min L Q,Su Y M,Kuang Y.Mathematical Analysis of a Basic Virus Infection Model with Application to HBV Infection[J].Rocky Mountain J Math,2008,38:1573-1584.

[13]秦曉慧,黃健群,董海瑞,等.現代控制理論與應用[M].北京:國防工業出版社,2007:186-191.

[14]Kamien M I,Schwartz N L.Dynamics Optimization:the Calculus of Variations and Optimal Control in Economics and Management[M].Netherland:Elsever Science,2000.