楊傳岡老師“平行四邊形的面積”教學設計片段

一、談話引入

1.回顧：這里有一組公園里花圃的圖片，這些花圃的形狀有你熟悉的圖形嗎？

2.啟發：（出示長方形、正方形）你會算這兩幅圖形的面積嗎？（從沒有具體數據到有小方格，每個方格邊長1厘米）三年級時用數方格的方法推導出了長方形、正方形的面積計算公式。

3.揭題：（出示一個平行四邊形）它的面積又該怎樣計算呢？這就是本節課要研究的內容。（板書：平行四邊形的面積）

【設計意圖】課始，給學生一個開放的游玩場景，讓學生從熟悉的圖片中回顧已學圖形，激活學生用數方格的方法推導長方形、正方形面積的方法記憶，為學習新課做好鋪墊。

二、方法探究

1.設疑。師：猜想一下，這個平行四邊形的面積可能會用哪個算式來計算呢？（6×5，6×4，5×4）

2.激思。這3種假設可能都正確嗎？要正確的話，應該有幾個？（提示：假設有可能都不對。）

師：數學思考不能只停留在假設階段，有了假設，更重要的是要尋找方法加以驗證。（板書：假設——驗證）

3.方法。師：你打算用什么方法來研究平行四邊形的面積計算方法呢？（數方格、轉化等。）

（1）師生活動一：數方格驗證。

第一層次：驗證第一、第三種假設。

學生小組合作，通過鋪、擺1平方厘米方格的辦法排除5×4，6×5兩種可能，教師指導學生深究錯因，逼近知識本質。

第二層次：驗證第二種假設。

指導學生先去掉多余部分，再將圖形內的零碎部分剪、切、移、拼成整格，從而直接數出面積數量（如上圖）。

初步結論：24個小正方形正好鋪滿這個平行四邊形，平行四邊形的面積為24平方厘米。（6是平行四邊形的底，4是這條底所對應的高）現在，你知道平行四邊形的面積怎樣計算了嗎？板書公式。

方法回顧：用先假設再驗證的方法得到了平行四邊形的面積計算方法是底乘高。

師：有一位科學家卻認為，只用一種方法來證明一個結論還遠遠不夠，還可以怎樣證明？

（2）師生活動二：轉化法。

第一層次：思想滲透。

下面兩個圖形面積相等嗎？

學生猜測后電腦驗證，教師啟發方法。（通過轉化，把不規則圖形通過剪、移、拼，轉化成長方形，面積不變。）

第二層次：數據實證。

（1） 操作實驗。

你能把一個平行四邊形轉化成長方形嗎？

活動小貼士：

① 選一選：從信封中任意選擇一個平行四邊形。

② 說一說：小聲商量一下，我們小組準備怎樣轉化。

③ 動動手：兩人一組，剪一剪、移一移、拼一拼，我們有什么發現？

小組活動，展示交流（突出展示剪法不同，轉化效果相同，即通過剪、移、拼，把平行四邊形轉化成了長方形）。

師：開普勒說過，數學就是研究千變萬化中不變的關系。

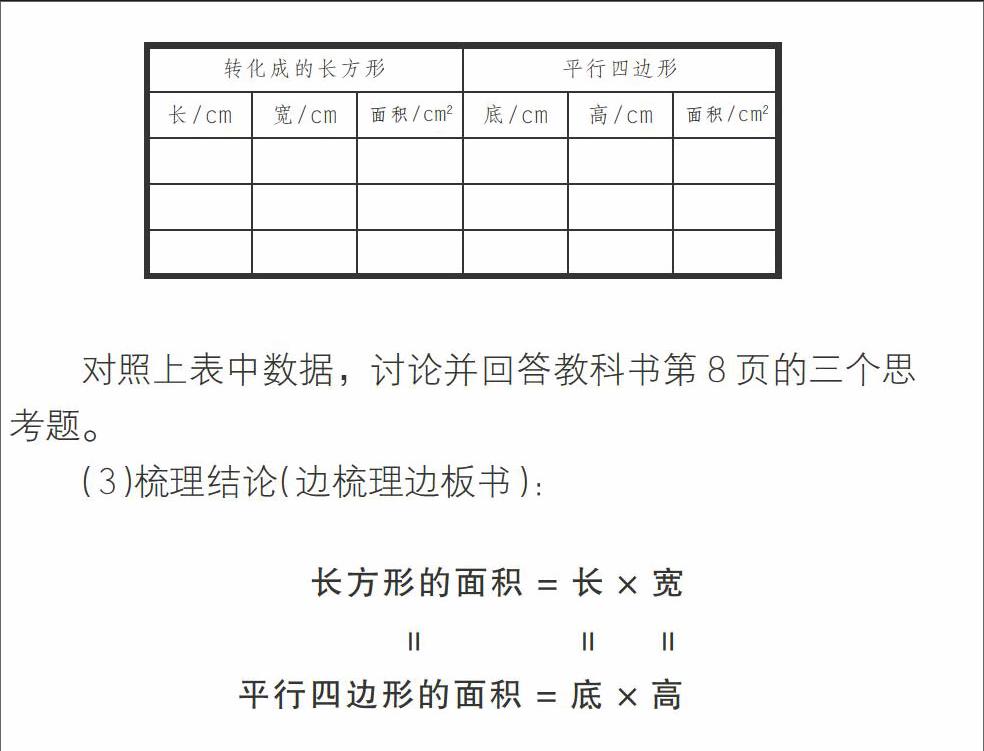
（2）數據整理

對照上表中數據，討論并回答教科書第8頁的三個思考題。

（3）梳理結論（邊梳理邊板書）：

（4）描述歷程：誰能說一說，平行四邊形的面積是怎樣推導的呢？

（5）字母表達：S=a×h。

【設計意圖】受長方形面積計算方法的定式思維的干擾，不少學生認為平行四邊形的面積等于相鄰兩條邊的乘積，這是學生認知中最大的障礙。為了突破這個難點，教師對教材進行了大膽重組，放開手腳讓學生在猜想驗證中自主探索，研究思路多元，研究方法開放。學生通過擺小方塊探究，逐一排除，初步得出平行四邊形計算方法；再用轉化法先操作后根據數據從兩個層次由表及里展開實證，層層剝筍直抵知識本質，建立平行四邊形面積計算的方法模型。教師從層層遞進中追根溯源，不斷釋疑明理。這種回歸思維原點的做法，讓學生在開放探究中深刻感悟到數學的本質，體驗到探索與發現的快樂。最終實現基礎知識習得、基本計算技能練習、數學思想方法滲透、基本活動經驗積累的四位一體的有機達成。

（作者單位：江蘇省鹽城市第二小學）

責任編輯：周瑜芽

Email：jxjyzyy@163.com