二重數值積分公式的構造

陳亞婷，郝粉霞,張雅靜，王會英

(河北農業大學理學院， 河北保定　071001)

二重數值積分公式的構造

陳亞婷，郝粉霞,張雅靜，王會英

(河北農業大學理學院， 河北保定071001)

摘要：為解決二重積分的近似計算問題，利用一個高精度的數值積分公式，推廣到二重積分，并對該公式進行了余項研究和誤差分析，最后通過幾個典型的例子驗證公式的有效性．

關鍵詞：數值積分公式；二重積分； 高精度

DOI：10.3969/j.issn.1000-1565.2015.02.002

中圖分類號：O241.4

文獻標志碼：志碼：A

文章編號?編號 1000-1565(2015)02-0118-04

Abstract:In order to solve the double integral approximation problem, a high order numerical integral formula was applied to extend it to the double integrals. Then，analyze the remainder and error of this formula. Finally, the high validities of this formula are proved by several typical examples .

收稿日期:2014-09-29

基金項目：保定市科學技術研究與發展指導計劃項目(14ZN001)； 河北省教育廳研究項目(z2014142)；保定市科學技術研究與發展指導計劃項目(12ZS006)

Construction of double numerical integration formula

CHEN Yating，HAO Fenxia, ZHANG Yajing，WANG Huiying

(College of Science，Hebei University of Agriculture，Baoding 071001，China )

Key words: numerical integration formula；double integrals；high order accuracy

MSC 2010：65D30

第一作者:陳亞婷(1981-)，女，河北張家口人，河北農業大學講師，主要從事計算數學方向研究.

E-mail: sxchenyating@hebau.edu.cn

隨著科學技術和計算機技術的日益發展，定積分和重積分的計算問題被廣泛地應用在信號處理、小波分析、自動控制、人工神經網絡等科學工程領域．一元函數的數值積分的近似計算已經得到較好的解決，比如Newton-Cotes公式、Gauss公式等[1-3]．但是二元函數的數值積分以及二元以上的數值積分也會遇到類似的問題需要解決．文獻[4-10]給出了一些二元函數的數值積分的構造方法和近似算法．

本文在文獻[11]的基礎上，利用該文構造的一元函數的數值積分公式，構造了一個二元函數的數值積分公式，并通過實際算例證明了該公式的有效性，可以很好地應用在實際問題中．

1構造公式

根據文獻[11]可知，如果被積函數f(x)在積分區間[a，b]上足夠光滑，并且在[a，b]上每一點處的二階導數都可求得，可構造如下的數值積分公式：

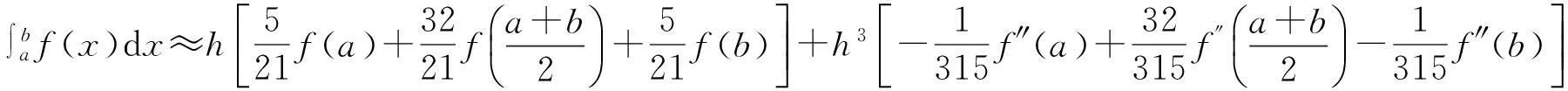
(1)

該求積公式具有7次代數精度，且余項

(2)

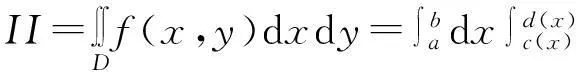
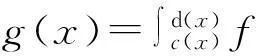
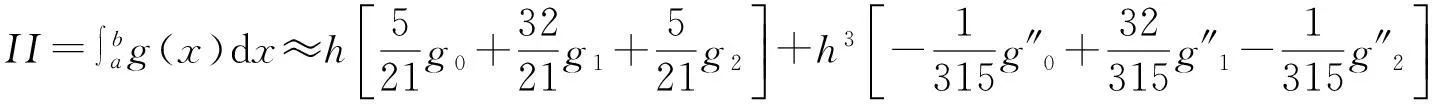
(3)

余項

下面求g0，g1，g2和g″0，g″1，g″2：

在[c(xi),d(xi)]應用公式(1)得

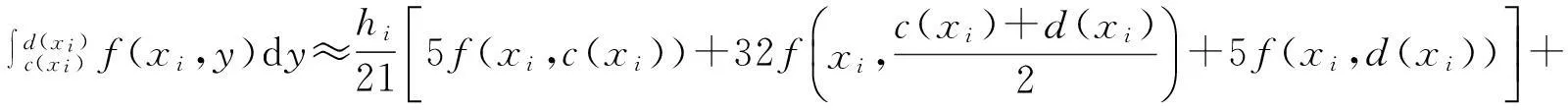
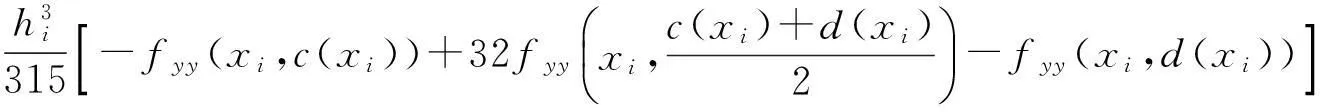
(4)

余項

f(xi,d(xi))d″(xi)+fx(xi,d(xi))d′(xi)+fy(xi,d(xi))d′2(xi)-f(xi,c(xi))c″(xi)-

(5)

f(xi,d(xi))d″(xi)+2fx(xi,d(xi))d′(xi)+fy(xi,d(xi))d′2(xi)-f(xi,c(xi))c″(xi)-

2fx(xi,c(xi))c′(xi)-fy(xi,c(xi))c′2(xi)．

余項

把gi，g″i，i=0,1,2代入公式(3)得二重積分的數值計算公式，其中余項

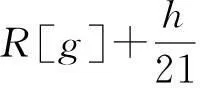
(6)

于是有如下結論：

定理1設函數f(x,y)在D={(x,y)|a≤x≤b,c(x)≤y≤d(x)}上充分光滑，c(x)，d(x)在[a,b]上連續且可微， 則公式有如下誤差估計：

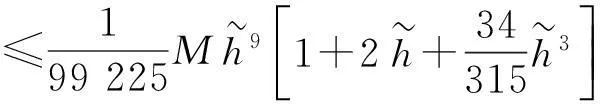
(7)

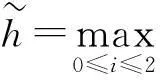
特別地 ，當D為矩型區域：D={(x,y)|a≤x≤b,c≤y≤d}時，

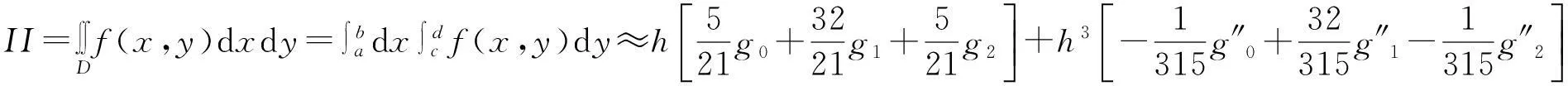
(8)

其中

(9)

(10)

2數值計算

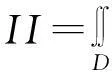
由于積分區域為矩形區域，則可利用公式(8)—(10)計算可得

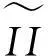
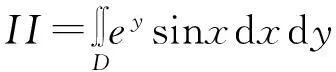
已知真值II=0.397 273 627 998 12.

3結果與討論

通過上面的數值計算結果表明：在計算二重數值積分時，本文構造的二重數值積分公式能很好地作為積分值的近似，而且精確程度較高．特別是積分區域為矩形區域時計算更為簡便．當然，如果積分區域為Y-型區域也可通過類似的方法求得積分值；如果積分區域是其他復雜的區域，則可把該區域分割成若干個X-型區域和Y-型區域，然后一一利用公式積分求和即可．本文的優點在于利用了較少的條件構造了一個精確程度較高的二重數值積分公式，由此用較少的計算量就可以達到精度的要求，同時，所得到的積分公式還易于編程，因而在實際計算中有廣泛的應用．該公式還可以進行復化，由此得到更高精度的數值積分公式，但是相對而言，復化公式較為復雜，是需要進一步研究的內容．

積分的計算是非常重要的計算，積分的數值算法在積分中顯得尤為重要．本文在文獻[11]的基礎上，利用該文構造的一元函數的數值積分公式，利用了較少的條件構造了一個精確程度較高的二元函數的數值積分公式，所得到的積分公式易于編程，因而在實際計算中有廣泛的應用．

參考文獻:

[1]李慶揚，王能超，易大義．數值分析[M]．北京：清華大學出版社，2008 .

[2]楊濤，王愛茹，王增輝．計算方法[M]．北京：中國水利水電出版社，2005.

[3]陳公寧，沈家驥.計算方法導引[M]. 北京：北京師范大學出版社，2009.

[4]吳新元，吳宏偉.一個新的高精度二重數值積分公式[J]．計算物理，1991,8(4):437-441.

WU Xinyuan ,WU Hongwei. A high accurate numerical integration formula[J]. Journal of Computational Physics，1991,8(4):437-441.

[5]陳付龍.二元數值積分的計算方法[J]．計算機工程與應用，2007,42(19):32-34.

CHEN Fulong. Two-dimensional numerical value integral's computing method[J]．Computer Engineering and Applications, 2007,42(19):32-34.

[6]朱振廣.復雜區域上的二重積分數值計算的一種方法[J]．遼寧工學院學報，2004,24(2):52-54.

ZHU Zhenguang. A method of estimating multivariable integral on complex region[J]．Journal of Liaoning Institute of Technology, 2004,24(2):52-54.

[7]王勇，熊華.多重Newton-Cotes積分及其系數[J]．西華師范大學大學學報：自然科學版，2010,31(3):271-274.

WANG Yong, XIONG Hua.Multiple Newton-Cotes integral and the coefficients [J]．Joumal of China West Normal University:Natural Sciences，2010,31(3):271-274.

[8]徐偉，鄭華盛，李曦．一類高精度數值積分公式的構造[J]．數學的實踐與認識，2012,42(18)：207-215.

XU Wei, ZHENG Huasheng, LI Xi. Constructions of new high accurate numericalintegration formula[J]．Mathematics in Practice and Theory，2012,42(18)：207-215.

[9]許江浩，陳志坤，劉斌．一個高精度數值積分公式[J]. 四川理工學院學報，2011,24(2)：168-170.

XU Jianghao, CHEN Zhikun, LIU Bin.A higher order accuracy numerical quadrature rule[J]．Journal of Sichuan University of Science & Engineering:Natural Science Edition, 2011,24(2)：168-170.

[10]鄭華盛，唐經綸，危地．高精度數值積分公式的構造及其應用[J]．數學的實踐與認識，2007,37(15)：141-148.

ZHENG Huasheng, TANG Jinglun, WEI Di. Constructions of high accurate numerical integration formula and its applications[J].Mathematics in Practice and Theory，2007,37(15)：141-148.

[11]陳亞婷，冀德剛，賈鸝，等. 利用二階導數構造的數值積分公式[J]．河北大學學報：自然科學版，2014,34(04):347-350.

CHEN Yating，JI Degang，JIA Li, et al. Numerical integration formula by second derivative[J]．Joumal of Hebei University：Natural Sciences，2014,34(04):347-350.

(責任編輯：王蘭英)