三目標混合骨干粒子群算法的電力系統無功優化

馬立新，王繼銀，項　慶，黃陽龍

(上海理工大學 光電信息與計算機工程學院，上海200093)

三目標混合骨干粒子群算法的電力系統無功優化

馬立新，王繼銀，項慶，黃陽龍

(上海理工大學 光電信息與計算機工程學院，上海200093)

摘要：電力系統無功優化通常以降低有功網損和減小電壓偏移為目標，建立了綜合考慮有功網損和電壓偏移最小及電壓穩定裕度最大的三目標無功優化模型。首次引入混合骨干粒子群算法用于解決電力系統無功優化問題。該算法利用關于粒子個體極值和全局極值的高斯分布對粒子位置進行更新，再通過K-均值聚類的方式，引入單純形法對有代表性的粒子進行單純形搜索，使算法既能夠具備較強的全局搜索能力，又能夠提高收斂速度和精度。將該算法和其他算法應用于IEEE-14節點系統中進行無功優化，通過數據的計算和比較，結果驗證了該模型和算法用于解決多目標電力系統無功優化問題的優越性和實用性。

關鍵詞：骨干粒子群；K-均值；單純形；三目標優化；電壓穩定裕度

中圖分類號:TM714

文獻標識碼:??碼: A

DOI:10.3969/j.issn.1672-0792.2015.11.004

收稿日期：2015-08-31。

基金項目：滬江基金(C14002)；上海市張江國家自主創新重點項目(201310-PI-B2-008)。

作者簡介：馬立新(1960-)，男，教授，主要研究方向為配電網規劃與優化配置、電力負荷需求分析與預測方法、調速系統智能控制等，E-mail:1215750647@qq.com。

Abstract：The reactive power optimization in power system usually aimes at reducing active network losses and voltage deviation, while the currently established three-objective reactive power optimization model considers the minimization of active network losses, voltage deviation and the maximum of voltage stability margin. To solve the reactive power optimization problem, hybrid bare-bones particle swarm optimization is introduced in this essay for the first time. The algorithm employs Gaussian distribution of particle individual extremum and global extremum to update particle location. Then it introduces simple method to search for the representative particles by the way of K-mean clustering. This algorithm not only tends to have strong global search ability, but also can improve the convergence speed and accuracy. The results of calculation and data comparison justify the superiority and practicality of this model and algorithm in solving multi-objective power system reactive power optimization problem. It is superior to algorithms when they are implemented on IEEE-14 node system.

Keywords：bare-bones particle swarm optimization；K-means；simplex method；three-objective reactive power optimization；voltage stability margin

0引言

隨著電力系統的完善，人們對系統運行的安全性越發重視，為了能更加明確顯示電力系統電壓運行點距離崩潰點的寬度[1]，本文建立了以節點電壓偏移最小，有功網損最少以及電壓穩定裕度最大為目標的三目標無功優化模型。

粒子群算法(Particle Swarm Optimizati- on,PSO)是一種群智能優化算法[2]。目前，標準PSO及相關改進算法用于解決RPO問題已有很多，但是由于標準PSO算法具有容易陷入局部極值，收斂速度慢等不足[3]，導致PSO算法在解決RPO問題上，未能取得很好的效果。

基于標準PSO的上述不足，本文引入了一種混合骨干粒子群算法(Simplex Method-Bare-Bones Particle Swarm Optimization,SM -BBPSO)[4],該算法是一種新興的全局優化技術，并將其首次應用于電力系統無功優化問題。該算法是利用骨干粒子群算法對粒子的位置進行更新，通過K-均值聚類的方式對粒子分類，再引入單純形法對各類中心粒子進行搜索，使算法既能夠具備骨干粒子群算法較強的全局搜索能力，又能夠由于單純形法的引入來提高收斂速度和精度，通過對IEEE-14節點系統的仿真計算，并與標準PSO及差分進化算(Differential Evolution, DE)法進行比較，驗證了本算法解決RPO問題的可行性及優越性。

1三目標無功優化模型

1.1　目標函數

本文以電壓偏移和有功網損最小及電壓穩定裕度最大為目標，建立優化模型。

(1)有功網損Ploss

(1)

式中：N為系統網絡總支路數；δi，δj是節點i、j的電壓相角；Gk(i,j)為支路k的電導；Vi，Vj是節點i、j的電壓。

(2)電壓偏移dv

(2)

(3)靜態電壓穩定裕度: 以收斂潮流中雅克比矩陣的最小特征值最大化，來作為電壓穩定的指標[5]。目標函數表達式如下：

(3)

式中：λmin是雅克比矩陣的最小特征值。

1.2　約束條件

(1)功率約束

保持功率平衡：

(4)

式中：Pi為有功功率；Qi為無功功率。

(2)變量約束

控制變量：

(5)

式中：VG為發電機的端電壓；T為可調變壓器的變比；QC為補償電容發出功率。

狀態變量：

(6)

式中：VL為負荷節點電壓；QG為發電機無功出力。

1.3　歸一化處理

由于各目標函數量綱不同，不能進行統一加權，故作如下歸一化處理：

(7)

式中：Ploss0,dv0分別為初始有功網損和電壓偏移；Plossmin,dvmin分別為進行單目標優化時得到的最優值；VSM本身無量綱，為使所求各目標函數有統一的最小值形式，故取倒數[5]。歸一化得到的總的目標函數如下：

(8)

w1,w2,w3分別為各目標函數的權值，且w1+w2+w3=1。

2粒子群算法和單純形法

2.1　標準粒子群算法

粒子群優化算法(PSO)是由Kennedy 和Eberhart根據鳥群覓食行為于1995年提出的一種群智能優化算法[6]，參數較少，操作簡單。PSO算法中每個粒子根據自己和同伴的飛行經驗來對速度和位置進行更新。公式如下：

(9)

(10)

式中：vij(k)，xij(k)分別為粒子i在第k次迭代中速度和位置的第j維分量；ω為慣性權重；c1、c2為學習因子；pij(k)為粒子i個體極值點位置的第j維分量；pgj(k)為粒子群體全局極值點位置的第j維分量；r1、r2為[0,1]之間的隨機數。

2.2　骨干粒子群算法

F.van den Bergh等人證明了在迭代次數趨向于無窮時，標準粒子群優化算法中的目標函數不是以概率1完全收斂于最優解[7]，Clerc和Kennedy通過分析粒子的飛行軌跡，得出粒子都向它的個體最優位置和全局最優位置的加權平均值收斂[8]即：

(11)

當迭代次數達到無窮大時，所有的粒子都將最終收斂到同一個點。根據這種理論，Kennedy于2003年提出了骨干粒子群算法(B BPSO)[6]。BBPSO是利用以(pij(k)+pgj(k))/2為均值，以|pij(k)-pgj(k)|為標準差的高斯分布對粒子位置進行更新：

(12)

N(.)是高斯分布。隨后，Kennedy又提出了骨干粒子群的另一種形式，采用下式對粒子位置進行更新：

(13)

大量的研究證實，骨干粒子群算法具備強大的全局搜索能力，而且不需設置各控制參數，算法更加優良。

2.3　單純形法

單純形法由Nelder與Mead提出的一種直接搜索方法，具備極強的局部搜索能力。其主要核心思想是：在一個n維空間中，構造出一個具有n+1個頂點的幾何體，分別求出各個頂點的目標函數值，確定出目標函數值最大，次最大，最小的頂點，求出除目標函數值最大頂點外其余n個頂點的形心，在每一次迭代中，通過反射、收縮、擴張等策略找出一個較好點來取代最大點，從而形成一個新的幾何體，通過這樣不斷地反復迭代，最終會找到或逼近一個局部最小解。

具體求解步驟如下：

(1)確定起始點。

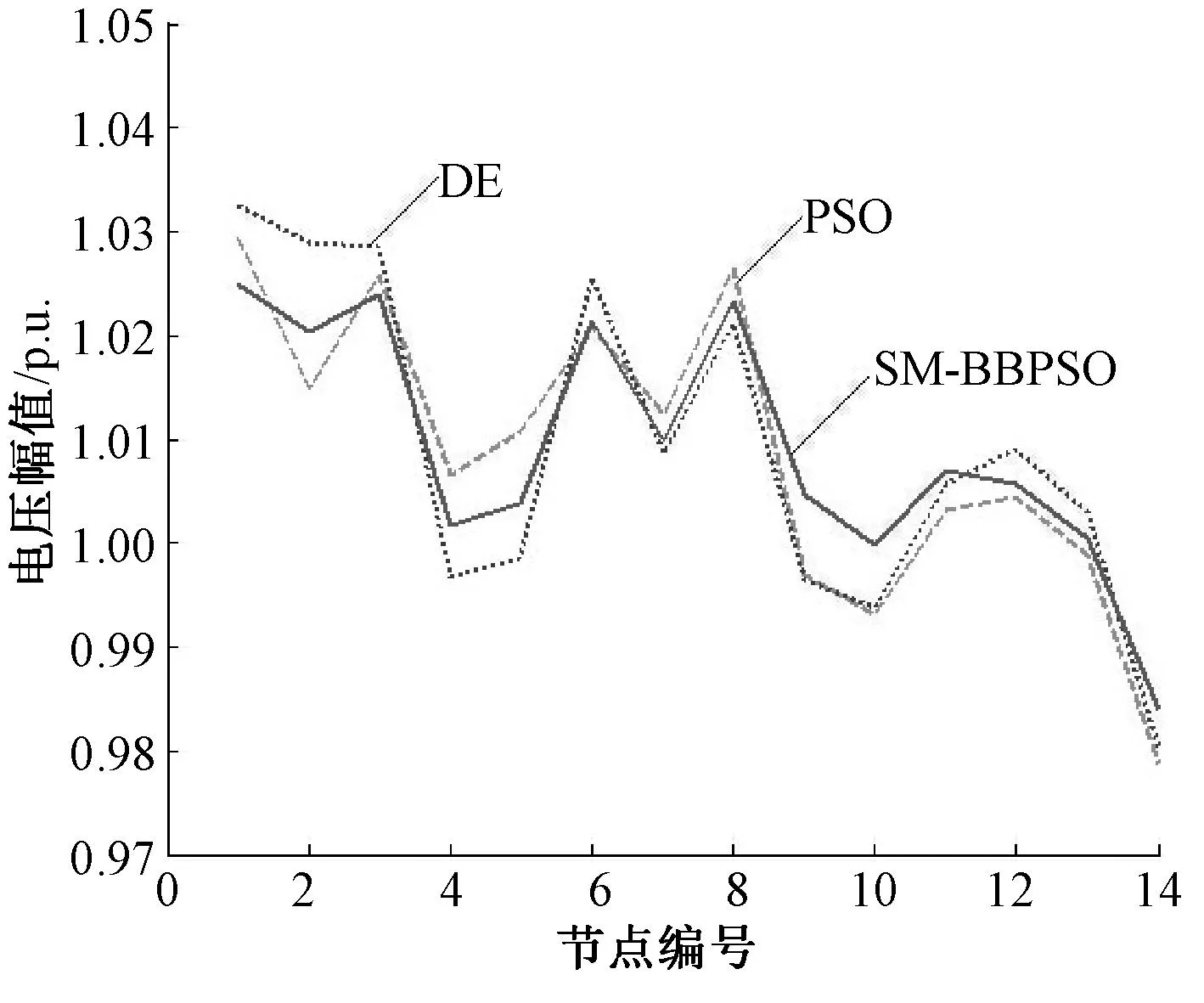
(2)反復操作:求出n+1個頂點的函數值, 確定其中的函數最大值fG、次大值fH和最小值fL, 除去函數值最大的點X(G)，并求出其他n個點的形心X,然后計算得出X(G)關于形心X的對稱點X(n+2),計算X(n+2)的函數值。若f(X(n+2))1, 其初始值可取2, 并計算X(n+3)的函數值。若f(X(n+3))

(3)若fL≤f(X(n+2)) ≤fH,則用X(n+2)取代X(G)并轉步驟(5)。

(4)若f(X(n+2))≥fH,則說明需要內縮。f(X*)=min{f(X(n+2)),f(X(H))},X(n+4)=X+β(X*-X), 其中β=0. 5,計算f(X(n+4))。若f(X(n+4))≤f(X*), 則用X(n+4)取代X(G)并轉步驟(5);若f(X(n+4))>f(X*),則進行縮邊,X(i)=(X(i)+X(L))/2,i=1, 2, …,n+1,并轉步驟(5)。

3混合骨干粒子群算法

盡管骨干粒子群算法有較強的全局搜索能力，然而也有收斂速度慢的不足，故引入單純形法，提高粒子的收斂速度。近年來，已有很多學者通過不同方式，把標準粒子群算法與單純形法結合來提高粒子群算法性能。文獻[9]、[10]分別是每一代和隔固定迭代次數對全局極值點進行單純形搜索，雖然這樣可以對粒子的質量有一定的提高，但是忽略了其他粒子得到的信息和經驗。文獻[11]是對每一個粒子進行單純形搜索，雖然利用了粒子之間的信息和經驗，但算法運算量較大，收斂時間上產生了代價。

本文運用K-均值聚類的方式來引入單純形，形成一種混合骨干粒子群算法(SM-BBPSO)。首先利用骨干粒子群算法對粒子位置更新，然后運用K-均值聚類的方式，隔一定迭代次數對粒子進行分類，對每一類中的中心粒子進行單純形搜索，使算法能夠充分利用各粒子的信息和經驗，增加種群多樣性，又能減少粒子收斂時間，提高算法性能。

無功優化步驟：

Step1：導入算法的基本參數包括種群規模，粒子分類數k，單純形搜索固定迭代次數K，以及對應電力系統中的潮流數據。

Step2：對粒子群體進行初始化，包括粒子的位置，速度，個體、全局極值，。

Step3：計算各粒子的適應度值并更新個體、全局極值。

Step4：判斷t/K=[t/K](取整)是否成立，若成立，跳向Step5,否則跳向Step6。

Step5：通過K-均值聚類的方法對粒子群進行分類，計算得出每類粒子群的中心粒子，對中心粒子實行單純形搜索，根據搜索結果，更新個體極值和全局極值。

Step6：按式(12)對粒子位置進行更新。

Step7：判斷是否符合終止條件，若符合則停止運行，否則跳向Step3繼續運行。

4算例及結果分析

為了驗證算法的有效性、優越性，對IEEE-14節點系統，進行優化測試，并與其他優化算法比較。

4.1　測試數據

IEEE-14節點系統共有20條支路，5臺發電機，3臺有載調壓變壓器,1個并聯補償電容器節點。具體變量設置如下：

1,2,3,6,8節點為發電機，取節點1為平衡節點，節點2,3,6,8為PV節點；節點9為并聯電容器安裝節點；除1,2,3,6,8節點外，其他節點均為PQ節點。支路5-6，4-7,4-9為變壓器支路。發電機端電壓變化區間為[0.95,1.10](標幺值，系統基準容量為100 MVA，下同)；變壓器變比調節區間為[0.90,1.10]，調節步長為0.012 5，即17檔；電容器可調節區間為[0.00,0.50]；分類數k為2，間隔代數K為3，單純形法代數為50。該系統初始有功網損、電壓偏移、電壓穩定裕度分別為0.133 8、2.945 0、0.518 0[12]。

4.2　優化結果分析

優化仿真結果如下所示。表1、表2為本算法與其他算法得出的數據比較。表1中有功網損、電壓偏移數值由圖1、圖2中最終收斂值反代入式(7)所得。由表1可知三目標優化后都比優化前有了顯著的提高，SM-BBPSO算法在有功網損上比DE、PSO算法分別減少0.89 %，1.3 %，比優化前減少8.4 %；電壓偏移，電壓穩定裕度也明顯優于另外兩種算法，可見本算法的優越性所在。

表1　IEEE-14節點系統各算法比較

表2　不同算法優化后控制變量的值

由圖1可知，SM-BBPSO算法在優化有功網損過程中，在迭代次數接近30時就逐漸趨向于平穩，收斂速度明顯快于DE、PSO算法，且有功網損數值明顯小于另外兩種算法，而有功損耗越小，則表明經濟性越好。

圖1　IEEE-14節點系統有功網損

由圖2有，SM-BBPSO算法在優化電壓偏移過程中，在迭代次數超過50時，才穩定，雖稍慢于PSO算法幾代，但在迭代次數達到10時，該算法收斂曲線仍然下降很快，且收斂值也明顯小于DE、PSO算法。可見該算法的優勢還是可觀的。而電壓偏移越小，則表明電網的穩定性越高。

圖2　IEEE-14節點系統電壓偏差

由圖3可知，SM-BBPSO算法在優化電壓穩定裕度過程中，在迭代次數達到40時，就逐漸趨于穩定，在收斂速度上顯然快于DE、PSO算法，且該算法電壓穩定裕度較大，而裕度越大，則更有利于電網的安全性。

圖3　IEEE-14節點系統電壓穩定裕度

各算法優化后的節點電壓的分布圖如圖4所示。

圖4　優化后各節點電壓分布

由圖4可看出，為了保證電源設備的安全運行，在迭代過程中，PV節點轉化為了PQ節點。SM-BBPSO算法優化后各節點電壓值更接近期望值Vi*，波動較小，使得系統總體的節點電壓偏移較小，明顯優于DE、PSO算法。

綜合以上可知，SM-BBPSO算法在同時對三個目標進行無功優化過程中，比起其他算法，不僅提高了解的質量和精度，也加快了收斂的速度，故可以更好地解決無功優化問題。

5結論

本文考慮有功網損、電壓偏移最小及電壓穩定裕度最大為目標，首次引入混合骨干粒子群算法用于解決電力系統無功優化問題。該算法利用骨干粒子群算法強大的全局搜索能力，提高了粒子質量，并借助K-均值聚類的方式引入單純形搜索，提高了收斂速度和精度。將該算法應用于IEEE-14節點系統中，通過比較，結果表明了該算法的優越性和實用性，為求解無功優化問題，提供了一個新的方法。

參考文獻:

[1]包黎昕，張步涵，段獻忠,等. 電壓穩定裕度指標分析方法綜述[J]. 電力系統自動化,1999,23(8)：52-55.

[2]盛四清，李婧，田文樹. 群智能算法在電力系統無功優化中的應用[J]. 電力科學與工程，2008,24(1)：1-4.

[3]馬立新，單冠華，屈娜娜. 基于改進粒子群算法的電力系統無功優化[J]. 控制工程，2012，(19)：14-18.

[4]王攀攀，史麗萍，張勇，等. 采用一種混合骨干微粒群優化算法的感應電機轉子斷條故障診斷[J]. 中國電機工程學報，2012，32(30)：73-81.

[5]李瑩，簡獻忠. 基于免疫進化細菌覓食算法的多目標無功優化[J]. 電力科學與工程，2014,30(4)：5-10.

[6]史麗萍，王攀攀，胡泳軍，等. 基于骨干微粒群算法和支持向量機的電機轉子斷條故障診斷[J]. 電工技術學報, 2014, 29(1)：147-155.

[7]Frans V D B.An analysis of particle swarm optimizers[D]. Particle Swarm Optimization, 2002.

[8]Clerc M，Kennedy J.The particle swarm-explosion，stability，and convergence in a multidimensional complex space[J].IEEE Transactions on Evolutionary Computation, 2002, 6(1)：58-73.

[9]安偉剛，李為吉.改進的粒子群優化算法及其工程應用[J].機械科學與技術，2005，24(4)：415-417.

[10]Hsu C C，Gao C H. Particle swarm optimization incorporating simplex search and center particle for global optimization[C].Japan：IEEE，2008：26-31.

[11]王芳，邱玉輝.一種引入單純形算子的新穎粒子群算法[J].信息與控制，2006，34(5)：517-522.

[12]馮士剛，艾芊. 帶精英策略的快速非支配排序遺傳算法在多目標無功優化中的應用[J]. 電工技術學報，2008，22(12)：146-151.

Three-objective Hybrid Bare-bones Particle Swarm Optimization for Reactive Power Optimization

Ma Lixin, Wang Jiyin, Xiang Qing，Huang Yanglong(School of Optical-Electrical and Computer Engineering, University of Shanghai for Science and Technology, Shanghai 200093, China)