兩自由度動力吸振器的頻響函數與有限元分析

田紅亮　周　揚　鄭金華　陳甜敏

(三峽大學 機械與動力學院， 湖北 宜昌　443002)

?

兩自由度動力吸振器的頻響函數與有限元分析

田紅亮周揚鄭金華陳甜敏

(三峽大學 機械與動力學院， 湖北 宜昌443002)

摘要：以兩自由度動力吸振器為實例，采用Matlab軟件繪出不同阻尼所對應的系統傳遞函數的Nyquist圖像．借用有限元分析軟件ANSYS對動力吸振器進行諧波響應分析，得出系統在不同頻率下的動態響應并討論響應量(通常是位移)與頻率之間的關系．同時動力吸振器系統自身的物理特性對其動態特性有影響．這能使設計者在設計產品的過程中全面地處理振動問題，以得到最優動態性能的系統．

關鍵詞：動力吸振器；傳遞函數；頻響函數；諧響應

動力吸振器是一種使用廣泛的減振設備，其結構簡單，可有效地解決頻率范圍變化不大的系統的共振問題，特別當外界激勵頻率變化范圍已知時，它能有效地抑制系統結構和設備的共振，它也是當前最方便、經濟與可靠的被動式控制方法[1]．一個實例可以簡單說明動力吸振器的作用，一臺動力機械(簡化為一個彈簧質量系統)構成一個振動系統，當其上作用的激振力F(t)=F0cosωt的頻率與系統固有頻率接近時，系統發生共振，振幅增大．為了改變這種狀況，可以改變系統的質量和彈簧剛度．為使系統離開共振區，當系統的質量和彈簧剛度不能改變時，可以在原系統上增加一個附加系統，這樣就可以使主系統振動狀況大大改善，這就是動力吸振器[2]．

為了改善動力吸振器的特性，許多科技工作者把安裝動力吸振器的結構響應或單邊功率譜密度看作評價減振效果，或者以得到最小的主質量位移方差作為動力吸振器的參數優化目標，或者利用功率流的計算方法．目前已有的部分工作的主要特點均是分析計算主系統吸振器組成的復合系統的動態性能，以得到吸振器參數，或者只簡化處理一些比較特殊的結構[3]．本文以一個兩自由度動力吸振器振動系統作為研究對象，運用機械振動學理論和有限元分析軟件探討動力吸振器系統頻響函數及相關參數對系統動態響應性能的影響規律．

1動力吸振器頻響函數

1.1動力吸振器頻響函數的求解

圖1所示結構為動力吸振器，質量m1、m2在水平方向上分別用兩個剛度為k1、k2的彈簧連接于支撐點．m1上作用一幅值為P0，頻率為f的正弦激勵力P(t)，在此激勵下，系統在水平方向上作往復直線運動．已知m1=m2=1 kg，k1=1 000 N/m，k2=500 N/m，P0=1 000 N．

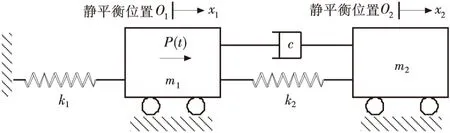
圖1　動力吸振器的物理模型

系統的運動微分方程為

根據式(2)、式(3)和文獻[4]得

根據式(5)和文獻[4]得

fn2比fn1大141.9%．根據文獻[4]得

根據式(10)和文獻[4]得

根據式(10)、式(11)和文獻[4]得

將式(1)寫為下面的復數形式

設方程(13)具有形如以下特解

根據式(13)、式(14)和文獻[4]得

根據式(15)和文獻[4]得

將式(16)代入式(14)得

故方程(1)的特解為

根據式(18)和文獻[4]，將式(15)展開得

最后根據文獻[4]得

1.2動力吸振器頻響函數圖像

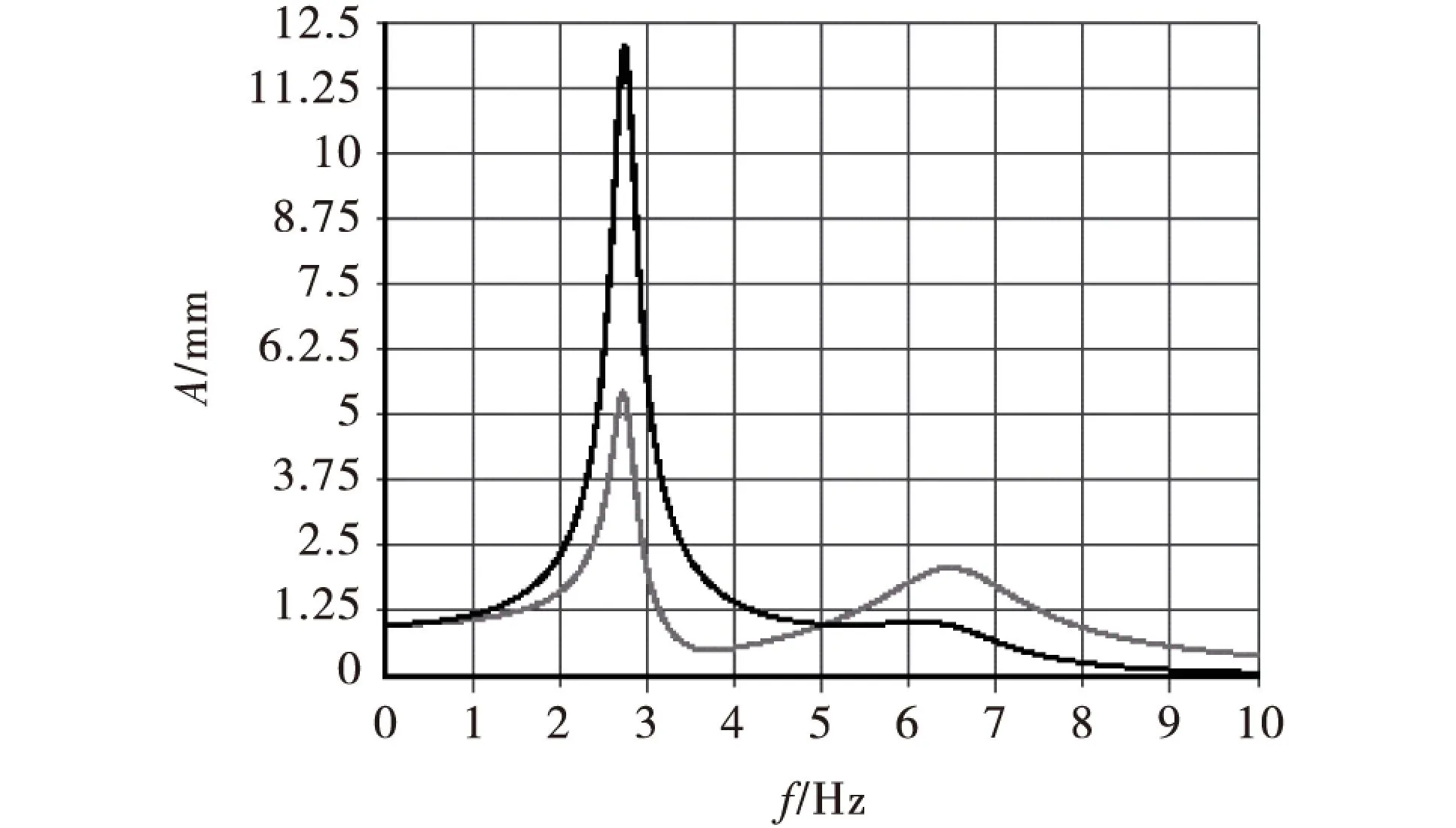
(a)H11(ω)的Nyquist圖　　　　　　　　(b)H21(ω)的Nyquist圖　　　　　　　(c)H11(ω)的實頻特性與虛頻特性圖2　系統的復頻響應函數

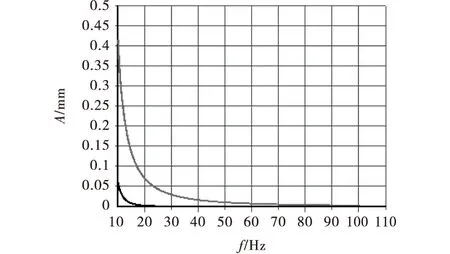
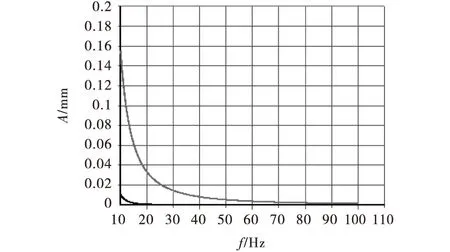
采用Matlab軟件編程，繪出不同阻尼所對應的系統傳遞函數的Nyquist圖像，同時繪制出頻率范圍為2Hz

2基于ANSYS的動力吸振器系統諧波響應分析

諧響應分析對持續的周期載荷在結構系統中產生持續的周期響應進行分析，其目的是確定線性系統承受隨時間按正弦規律變化的載荷時的穩態響應．諧波響應分析步驟主要分為：有限元建模，加載求解和結果分析[6]．在這里必須特別注意的是在加載求解過程中，所取諧波頻率范圍必須包括對系統結構動態特性影響較大的頻率，即模態固有頻率，且頻率間隔劃分要十分精細，只有這樣才能提高多自由度系統在頻域內的諧波響應分析精度．

現以兩自由度系統動力吸振器為例，介紹運用有限元分析軟件ANSYS獲取多自由度系統的諧波響應的具體方法[7-8]．

2.1動力吸振器系統物理模型的描述與有限元模型的建立

如圖1所示的結構為動力吸振器，質量m1、m2在水平方向上分別用兩個剛度為k1、k2的彈簧連接于支撐點，m1上作用有一幅值為P0，頻率為f的正弦激勵力P(t)，已知f=0～10 Hz．該系統在任一瞬時的位置都需用兩個獨立廣義坐標x1，x2確定，它是兩自由度系統．

根據系統物理模型直接建立有限元模型，如圖3所示，由3個節點、4個單元組成．

圖3　動力吸振器系統有限元模型

具體步驟如下：1)創建節點1、2、3；2)在相鄰節點之間建立彈簧阻尼單元①、③，類型均為combine14，用直線表示，剛度和阻尼系數分別為(k1，0)、(k2，c)；3)在節點2和3上創建質量單元②、④，類型均為mass21．所有單元在Y、Z方向的質量及繞X、Y、Z軸的轉動慣量都為零，而單元②、④在X方向上的質量分別為m1、m2．

2.2動力吸振器系統有限元模型的加載求解及諧波響應的計算結果分析

對系統有限元模型加載求解，步驟如下：1)設定響應分析類型為“Harmonic”；2)設定激振頻率范圍為0

描述系統的諧波響應結果，要采取ANSYS的后置處理程序，即時間歷程后處理器，它可以很方便地得出m1、m2的振幅A與激勵力的頻率f之間的關系，如圖4所示．該系統具備2階固有頻率，分別為f1=2.72 Hz，f2=6.58 Hz．當激勵頻率f位于f1或f2附近時，系統發生共振，m1、m2的振幅達到最大．

注釋：圖4、6、7與8中，f1處對應幅值A較大的一條為m2的幅頻特性曲線；圖5、9中，上面的一條曲線為m1的幅頻特性曲線．

圖4　m1、m2的幅頻特性

2.3動力吸振器的系統參數對動態性能的影響

為深度分析動力吸振器系統自身的結構參數對其動態特性的影響，需運用控制變量法分別單獨改變彈簧剛度、阻尼、質量等參數的大小作類似分析，最后討論在高頻范圍內質量對振幅大小的影響[9]，上述研究所得系統諧波響應的結果如圖5～9所示．

圖5　k1=2 000 N/m，k2=1 000 N/m時m1、m2的幅頻特性

圖6　c=6 N·s/m時m1、m2的幅頻特性

圖7　m1=m2=2 kg時m1、m2的幅頻特性

圖8　f=10～100 Hz時m1、m2的幅頻特性

圖9　f=10～100 Hz且m1=m2=2 kg時m1、m2的幅頻特性

各圖像結果對比分析如下：根據圖4和5可得，在低頻段，即f?f1時，系統振動非常慢，振幅的大小主要依賴于彈簧剛度，彈簧剛度越大，共振頻率也越大，系統的共振幅值減小，靜態特性突出．由圖4與6得出，在共振區，即f=f1或f=f2時，系統發生共振，振幅的大小主要取決于阻尼，阻尼增大，振幅減小．按照圖4和7可知，質量增大，共振頻率減小，系統的共振幅值增大．比較圖8和9可得，在高頻段，即f?f2時，系統振動很快，動態特性突出，振幅的大小主要取決于質量，質量越大，振幅越小．

參考文獻：

[1]丁文鏡．減振理論[M]．北京：清華大學出版社，1988：40-60．

[2]黃永強，陳樹勛．機械振動理論[M]．北京：機械工業出版社，1996：59-63．

[3]袁玲．兩自由度系統的動力吸振器參數最優化設計[J]．湖南工業大學學報，2007，21(2)：46-48．

[4]田紅亮，鄭金華，方子帆，等．阻尼系統的特征[J]．三峽大學學報：自然科學版，2015，37(2)：75-82．

[5]楊叔子，楊克沖，吳波，等．機械工程控制基礎[M]．5版．武漢：華中科技大學出版社，2006：120．

[6]商躍進．有限元原理與ANSYS應用指南[M]．北京：清華大學出版社，2005：180-220．

[7]黃文．基于ANSYS的多自由度系統的諧波響應分析[J]．機電產品開發與創新，2003(4)：58-59，69．

[8]Zeng Zhiping, Li Jun, Zhang Shiyi, et al． Analysis of the Harmonic Response of a Modulation Permanent Magnetic Transmission Equipment Based on ANSYS[J]． Energy and Power Engineering, 2015, 7:63-70．

[9]陳喜春，王俊麗．多自由度系統的諧響應分析[J]．蘭州交通大學學報：自然科學版，2007，26(1)：124-126．

[責任編輯張莉]

Frequency Response Function and Finite Element Analysis of

Dynamic Absorber with Two Degrees of Freedom

Tian HongliangZhou YangZheng JinhuaChen Tianmin

(College of Mechanical & Power Engineering, China Three Gorges Univ., Yichang 443002, China)

AbstractMatlab software is applied to draw the Nyquist images of the system transfer function under different dampings, taking the dynamic absorber with two degrees of freedom for example, the finite element analysis software ANSYS is utilized to arrive at the harmonic response analysis of the dynamic absorber. The dynamic response is obtained under various frequencies and the corresponding relationship between the response (ordinarily displacement) and frequency is analyzed. Meanwhile, the physical properties of dynamic absorber system have an impact on its dynamic characters. It can make the designer roundly handling vibration problems in the process of designing product to get system of the optimal dynamic performance.

Keywordsdynamic absorber;transfer function;frequency response function;harmonic response

中圖分類號：TH113.1

文獻標識碼：A

文章編號：1672-948X(2015)06-0091-04

DOI：10.13393/j.cnki.issn.1672-948X.2015.06.019

通信作者：田紅亮(1973-)，男，副教授，博士，研究方向為赫茲．E-mail： thl19732003@aliyun.com