小波函數預測控制技術應用

趙澤福

(昭通學院 數學與統計學院， 云南 昭通　657000)

?

小波函數預測控制技術應用

趙澤福

(昭通學院 數學與統計學院， 云南 昭通657000)

摘要：利用小波的緊支局部特性以及多尺度分析方法，在時域范圍內設置基函數的個數及位置分布以保證整體性能及擬合的逼近。仿真驗證了該方法的可行性。

關鍵詞：預測； 小波； 基函數

0引言

預測函數控制(PFC)是由Richalet與Kuntze提出的第三代模型預測控制算法，其快速的適應性、高精度算法控制以及較少的計算量使其已經廣泛應用于機器人控制、雷達跟蹤、熱焓控制等領域[1]。近年來，PFC在工業領域得到了快速發展，其理論基礎也得到不斷完善，如PFC算法內模結構、一階加純滯后過程和二階模型預測函數控制、自適應預測函數控制等。

針對不同的受控對象特性及其參考軌跡，在選擇基函數時可取階躍、斜坡、指數,甚至三角函數等[2]。該類基函數計算簡單、意義明確，但目標函數均是全局函數，簡化了優化要求或者僅對一兩點進行擬合，不能發揮其整體預測優化能力，弱化了整體參考軌跡的預測逼近性能，降低了其抗干擾性和精確性。雖然基于傅里葉逼近思想的正弦多項式函數在控制性和適用性上得到了加強，但由于控制策略為滾動優化式，對于精確求解對象的當量控制及未來控制是不必要的。通常情況，參考軌跡的逼近可以通過預測函數的時域減弱特性，利用集結方式將優化變量用低維方式代替，這樣不僅能夠減少計算量，還可以提高計算速度，從而滿足實時要求。針對時域減弱特性的靈活便捷設置，三角正弦函數同樣也無法滿足要求。文中提出的基于小波函數的預測函數控制技術方法通過實際仿真得到了有效驗證。

1小波函數理論基礎

小波理論是上世紀80年代應用數學和工程領域的重要產物。預測函數控制的基函數選擇對于快速高精度控制極其重要，而小波的緊支局部特性以及多尺度分析特性彌補了全局函數的不足。與傳統方法相比，小波通過伸縮和平移使得在時域和頻域上具有很強的局部特性，根據需要可以將所研究的內容聚焦到任意微小的細節。對于PFC，當軌跡逼近要求較高精度時，可以選擇小尺度的小波基函數，當對軌跡逼近精度要求低時，可以采用大尺度小波基函數。這樣既可滿足整體優化的同時，又兼顧了參考軌跡逼近的精度，在減少基函數的同時，也減少了權系數優化數量，完成了優化變量集結。基于此，文中將小波函數作為基函數應用于預測函數控制,利用加權最小二乘法計算權系數[3]。

設φ(t)∈L2(R)，當定義φ(t)為小波函數，則小波基函數為:

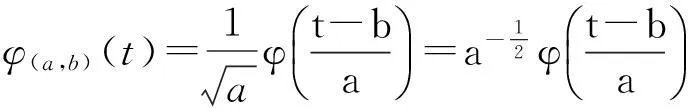
(1)

式中：a----尺度因子;

b----平移因子。

若a,b不斷變化，則可得到新函數φa,b(t)。

根據小波函數定義可知,當函數φa,b(t)中的a發生變化時，可以反映出小波函數的不同尺度。隨著a的不斷增大，函數時寬增加，亦即用伸展的φ(t)去觀察信號或函數f(t); 隨著a的不斷減小，函數時寬壓縮，表示用壓縮的φ(t)去觀察信號或函數f(t)，亦即用尺度因子的變化來表征信號或函數f(t)的局部信息。通過小尺度的變化反映高頻成分，大尺度的變化反映低頻成分，以上特性便是小波的多尺度分析特性。另外，由于小波∫Rφ(t)dt<∞,φ(t)具有很快的衰減性，即是說φ(t)的非零域具有有限性，在時域范圍內具有緊支集，很顯然小波函數的局部化能力非常強，因此也就具備了時域緊支局部性。文中利用小波的緊支局部特性以及多尺度分析，通過對基函數的個數及位置分布在時域范圍內的靈活設置，保證整體性能及擬合的逼近，實現了基于小波基函數的預測函數控制。

2基于小波函數的預測函數控制技術應用分析

預測函數控制的基礎為模型預測控制，其模型基本特征主要包括3個方面：預測模型、滾動優化和反饋校正[4]。同時PFC自身也有相應的特點，主要為關鍵性的控制輸入結構，通過預先選定的控制輸入量作為基函數的線性加權，使輸出作為對象的響應，實現目標函數的優化，求取加權系數，從而達到計算控制輸入的目的。

2.1　預測模型

預測模型是預測函數控制的重要部分，主要用于描述目標對象的行為動態，預測過程的輸出。對于其結構形式無需做過多的要求，重點在于完善其預測功能。預測系統的預測模型狀態方程可表示為[5]:

Xm(k)=EmXm(k-1)+Fmu(k-1)

(2)

式中：Xm----狀態向量,Xm∈Rn×1；

u----控制輸入,u∈R1×1；

ym----預測模型輸出,ym∈R1×1;

Em,Fm----狀態方程系數矩陣,Em∈Rn×n,Fm∈Rn×1;

Cm----狀態方程向量,Cm∈R1×n。

預測函數控制的具體形式為：

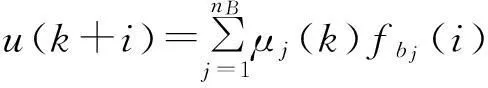
(3)

0≤i≤h

式中：μj----加權系數；

fbj----t=iT時的取值；

nB----基函數的個數；

h----時域長度。

預測模型的作用就是直接實現輸入量對輸出量的預測，模型的輸出ym(k+i)可以表示為：

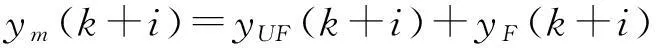
(4)

式中:yUF----自由響應輸出，u=0；

yF----受迫響應。

其中yF可以由下式求得：

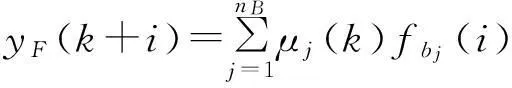
(5)

式中:fbj----在基函數fbj(i)作用下的模型輸出。

由式(3)，(4)和式(5)得

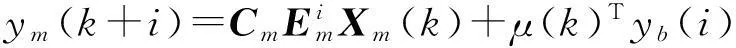
(6)

其中

μ(k)=[μ1(k),μ2(k),…,μnB(k)]T

yb(i)=[yb1(k),yb2(k),…,ybnB(k)]T

式(6)為模型輸出,其中ybj(i)為在基函數ybj(i)作用下的線性疊加，只有加權系數μj(k)需要在線求解。

2.2　優化算法

預測函數控制優化的目標就是要找到一組系數，使得在整個優化時域內的預測輸出盡可能接近參考軌跡。對于二次型性能指標可以通過擬合點上預測過程的輸出yp與參考軌跡yR差值的平方和最小來表示[6]，即

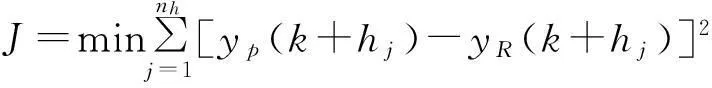
(7)

式中：nh----擬合點的個數，且nh≥nB;

hj----第j個擬合點的值。

參考軌跡選取指數形式：

(8)

式中：yR(k+i)----(k+i)時刻參考軌跡的值；

s(k)----設定值軌跡；

yp----實際過程輸出；

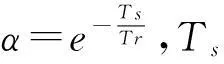
sb(k)----多項式系數；

Bs----多項式階數[7]。

3仿真實例分析

文中以原油精餾塔為仿真對象，利用基于小波函數的預測函數控制方法進行仿真[8]，并將結果與傳統算法進行對比。其輸入輸出對象模型可表示為：

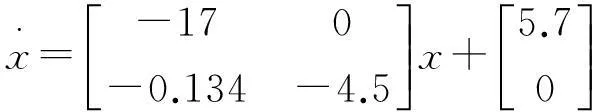
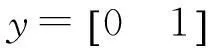
求出系統離散狀態方程系數矩陣為:

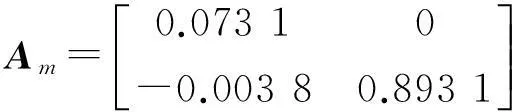
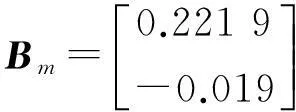
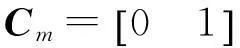
現假設模型Am,Bm失配而變為:

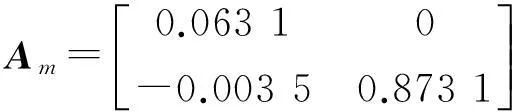
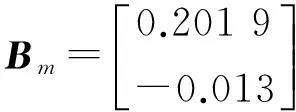
仿真參數選取：采樣周期Ts=1 s；參考軌跡閉環響應時間Tr=1.5 s；預測時域優化長度H=8;仿真時間50 s。由此可得仿真效果如圖1所示。

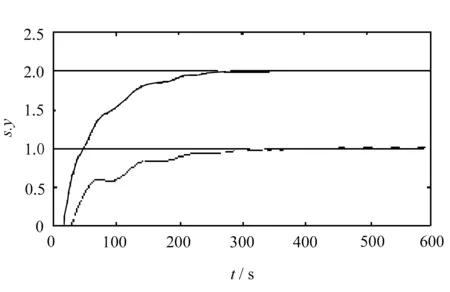
(a) 傳統仿真效果

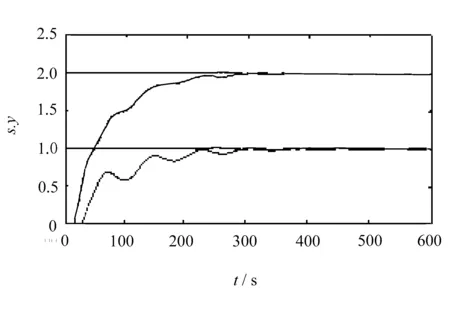
(b) 小波仿真效果圖1　仿真對比圖

由圖1可以看出，文中提出的小波基函數的整體優化性能以及軌跡逼近精度均優于傳統算法。

4結語

基于小波函數的預測函數控制方法有效地解決了傳統預測函數中基函數的不足，利用小波函數的緊支局部特性以及多尺度分析特性完成了不同情況下的仿真比較。通過仿真結果可以得出，該方法計算簡單、速度更快，對于工程應用更易實現。相比傳統控制方法中的基函數在精度控制、參數變化抑制和抗干擾性能上有了較大程度的改善，在快速工程應用領域具有重要意義。

參考文獻：

[1]Richalet J， RaultA， Testud J L， et al. Model predictive heuristic control: Applications to industrial processes[J]. Automatica,1978,14:413-428.

[2]侯寧,費樹岷,周磊.基于小波函數的預測函數控制方法研究[J].西南大學學報：自然科學版,2014,36(2):136-142.

[3]鄭軍,顏文俊,諸靜.基于小波基函數的預測函數控制[J].控制與決策,2005,20(9):1078-1080.

[4]杜曉寧,席裕庚.預測控制優化變量的集結策略[J].控制與決策,2002,17(5):563-566.

[5]AlbertB,FrancisJN.Afirstcourseinwaveletswithfourieranalysis[M].Beijing:PublishingHouseofElectronicsIndustry,2003:183-227.

[6]劉春雪,陳在平,董恩增.預測函數控制在網絡控制系統的應用[J].天津理工大學學報,2009,25(1):29-32.

[7]潘紅華,胡家升,朱森，等.一種改進的預測函數控制法[J].系統工程與電子技術,2003,25(11):1389-1391.

[8]周明月,姜文龍.基于小波變換的圖像混合去噪算法[J].長春工業大學學報:自然科學版,2008,29(2):162-164.

A wavelet function based prediction method

ZHAO Ze-fu

(School of Mathematics and Statistics， Zhaotong University, Zhaotong 657000, China)

Abstract：With the local properties of wavelet and multi-scale analysis method, both the number and position of the basis functions, in time domain, are set to ensure the ensure the overall performance and fitting approach. Simulation has verified the feasibility of the method.

Key words：predictionl； wavelet function； basis function.

作者簡介：趙澤福(1974-)，男，漢族，云南鎮雄人，昭通學院講師，主要從事基礎數學及微積分方程競賽數學方向研究,E-mail:mxc195611@163.com.

收稿日期：2015-01-25

中圖分類號：O 174

文獻標志碼：A

文章編號：1674-1374(2015)01-0097-04

DOI:10.15923/j.cnki.cn22-1382/t.2015.1.20