重參數化的多分屬性診斷分類模型及其判準率影響因素*

詹沛達 邊玉芳 王立君

(1北京師范大學 中國基礎教育質量監(jiān)測協同創(chuàng)新中心, 北京 100875)

(2浙江師范大學 心理系, 金華 321004)

1 引言

目前, 診斷分類評估(diagnostic classification assessment, DCA)已經受到了國內外學者的廣泛關注, 在教育與心理測量實踐中具有光明的未來。而診斷分類模型(diagnostic classification models,DCMs) (Rupp, Templin, & Henson, 2010)是對 DCA數據進行分析的必要工具。至今, 國內外學者已經開發(fā)了眾多的 DCMs, 常見的有 DINA (Junker &Sijtsma, 2001)、DINO (Templin & Henson, 2006)、LLM (Maris, 1999)、GDM (von Davier, 2005)、LCDM(Henson, Templin, & Willse, 2009)、G-DINA (de la Torre, 2011)、HO-DINA (de la Torre & Douglas, 2004)等等。

但縱觀現有的 DCMs, 絕大部分是基于二分屬性(dichotomous attributes, e.g., 用“0 和 1”分別表示“未掌握”和“掌握”)和二分 Q 矩陣(dichotomous Q-matrix, Q) (Tatsuoka, 1983, 1985)建構的, 而對多分屬性(polytomous attributes)和多分 Q矩陣(polytomous Q-matrix, Q) (Karelitz, 2004)的關注并不多(e.g., Karelitz, 2004; von Davier, 2005; Chen &de la Torre, 2013; Sun, Xin, Zhang, & de la Torre,2013)。而在實際教學和測驗中更多情況是對知識技能(i.e., 屬性)的多水平要求和考查, 比如《全日制義務教育數學課程標準(修改稿)》中就使用了“了解(認識)”、“理解”、“掌握”和“運用”這 4 個順序類別詞匯來表述知識技能目標的不同水平, 具有現實應用價值和前景。此時, 若想進行 DCA則應使用順序類別屬性編碼(ordered-category attribute coding,OCAC) (Karelitz, 2004)來對屬性的各個水平(類別)進行編碼(e.g., 用“0至3”分別表示上述4個順序類 別詞匯, 或用“0至 2”分別表示“掌握很差”、“掌握一般”和“掌握很好”)。多分屬性比二分屬性能提供更詳細的診斷信息、更具有實際應用價值, 且能夠對被試做出更為精細地劃分。傳統的二分屬性可被視為多分屬性的特例, 進而基于二分屬性的 DCMs就無法處理此類情況, 因此很有必要開發(fā)一些適用于處理多分屬性的 DCMs (polytomous attributes DCMs, Pa-DCMs)。

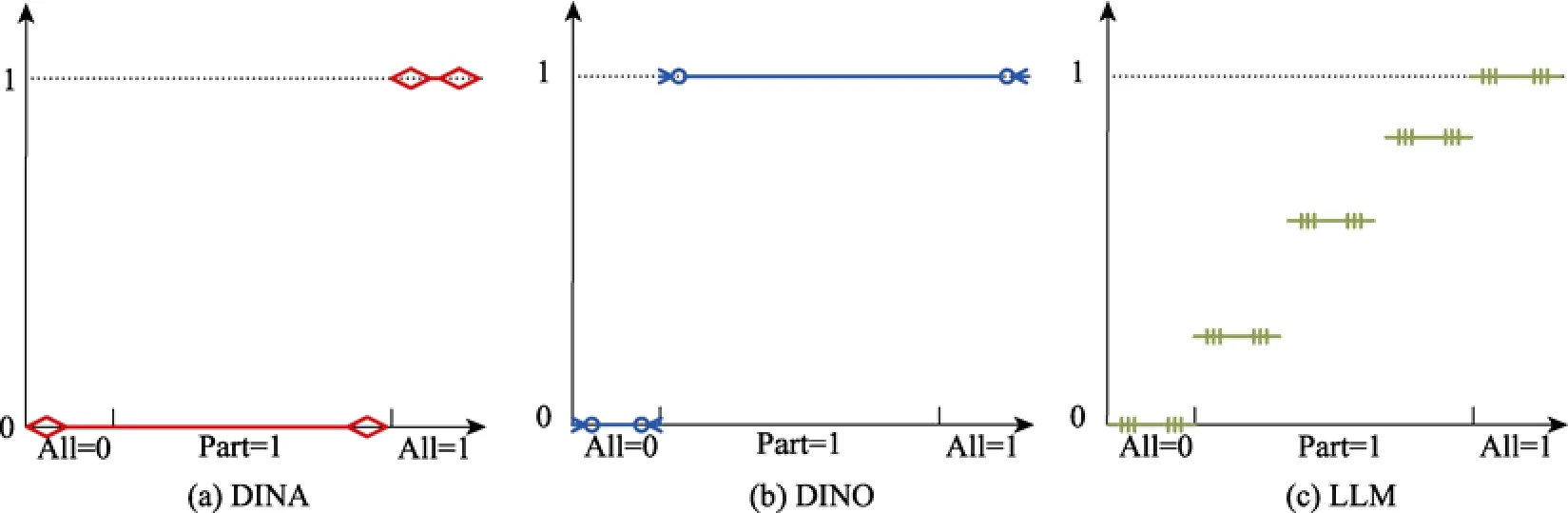
圖1 三種具有代表性的診斷分類模型的理想作答概率示例

查閱國內外相關文獻, 目前關于 Pa-DCMs的研究還處于初期探索階段, 僅有少許DCMs可以處理多分屬性(e.g., Karelitz, 2004; Templin, 2004; von Davier, 2005; Chen & da la Torre, 2013), 而其中基于OCAC的僅有OCAC-DINA (Karelitz, 2004)和pGDINA (Chen & de la Torre, 2013)。OCAC-DINA限制了所有題目擁有相同的題目參數; 而 pG-DINA因涉及到G-DINA (de la Torre, 2011)的相關概念,所以理解和解釋起來稍顯麻煩, 不利于多分屬性在實際應用中的推廣。為簡化理解難度, 可嘗試將pG-DINA按不同的縮合規(guī)則(condensation rule)(Maris, 1995, 1999)進行約束轉化。在DCMs中通常假設各屬性對正確作答概率存在3種貢獻方式或縮合規(guī)則：連接(conjunctive)、分離(disjunctive)和補償(compensatory) (詹沛達, 李曉敏, 王文中, 邊玉芳, 王立君, 2015), 其代表模型分別是 DINA、DINO和LLM, 如圖1所示, 可發(fā)現3類縮合規(guī)則的主要差異在于假設被試掌握部分屬性(Part = 1)時的正確作答概率不同, 補償可以視為連接和分離的折中。目前, 滿足連接縮合規(guī)則的診斷分類方法被研究的較多, 而滿足分離和補償縮合規(guī)則的診斷分類方法目前還未被充分挖掘, 具有很高待研究前景。另外, 國內關于多分屬性的相關研究也處于相對匱乏階段(e.g., 丁樹良, 羅芬, 汪文義, 熊建華,2015)。此外, 也未發(fā)現有相關研究在多分屬性情境下探討Pa-DCMs判準率的影響因素。

對此, 本研究將從兩方面切入, 第一部分對應二分屬性情境下具有代表性的 DINA、DINO和LLM, 分別給出 3種易理解且易解釋的重參數化Pa-DCMs (reparametrized Pa-DCMs, RPa-DCMs)表達式：RPa-DINA、RPa-DINO和 RPa-LLM; 第二部分則基于多分屬性的數量、多分屬性的最高水平數、各多分屬性之間的相關性、多分屬性間的層級結構、被試量和題目數這6個潛在的影響因素來探討新模型的判準率。需要強調的是因為 3個RPa-DCMs基于不同的縮合規(guī)則, 所以關于3者的探究是平行進行的。

2 三種具有代表性的RPa-DCMs

2.1 多分屬性和多分Q矩陣

Q矩陣(

I

×

K

, 其中

I

表示題目數量,

K

表示屬性數量)是連接題目與屬性的紐帶, 通常 Q矩陣是由0與1所組成的, 它的元素

q

界定了題目

i

與第

k

個屬性間的關系, 若

q

= 1表示題目

i

考查了第

k

個屬性, 反之為

q

= 0。而作為Q矩陣的拓廣, Q矩陣是由非負整數所組成的(Karelitz, 2004), 它的元素

q

界定了題目

i

對第

k

個屬性考查水平。式(1)和式(2)分別列出了相對應的Q矩陣和Q矩陣,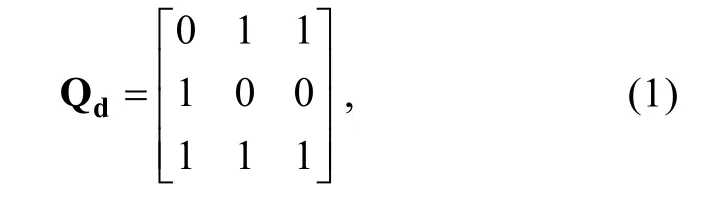

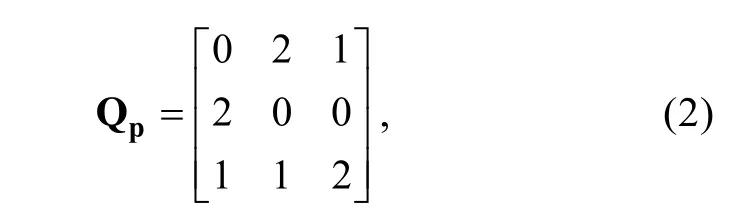
以第1題為例, Q矩陣描述了第1題考查了第2和第3個屬性, 而Q矩陣不僅描述了第1題考查了第2和第3個屬性, 且描述了第1題對第2個屬性的考查水平相對更高。因此, Q矩陣比 Q矩陣能提供更多的診斷信息。

2.2 RPa-DINA簡介

二分屬性情境下的DINA由于其參數較少、計算簡便且易于解釋等特點, 近些年得到了國內外較廣泛的關注和研究(e.g., de la Torre, 2008, 2009;Huang & Wang, 2014; Li & Wang, 2015; 涂冬波,蔡艷, 戴海崎, 丁樹良, 2010; 詹沛達等, 2015; 詹沛達, 邊玉芳, 2015)。Maris (1995, 1999)將連接縮合規(guī)則(conjunctive condensation rule)描述為：

式中,

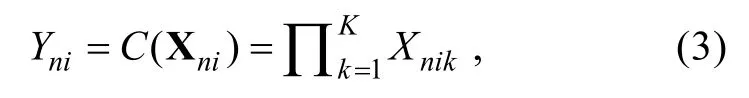
Y

表示在作答題目

i

時, 被試

n

的顯變量;

X

表示在作答題目

i

時, 被試

n

的第

k

個潛變量;

C

函數為縮合規(guī)則。則式(3)表示當且僅當

K

個

X

均為1時,

Y

才為1。應用至DCA中, 則表示當被試

n

掌握題目

i

考查的全部

K

個屬性時, 其理想正確作答概率才為1。

相對于 Chen和 de la Torre (2013)給出的Pa-DINA表達式, 本研究給出一種理解和解釋起來相對簡單且與之等價的RPa-DINA表達式：

另外, 當

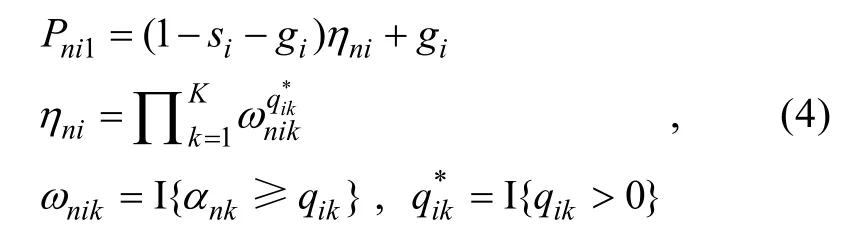
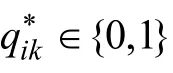
L

= 1時式(4)就可直接用于描述DINA, 無需做任何形式上的改變, 這符合“DINA應是RPa-DINA的約束模型(特例)”這一基本邏輯。

2.3 RPa-DINO簡介

DINO與DINA的區(qū)別是假設各屬性之間滿足分離縮合規(guī)則(disjunctive condensation rule) (Maris,1995, 1999)：

各參數含義同上, 其表示任意第

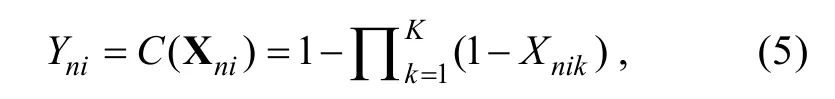
k

個

X

為1時,

Y

就等于1。應用至DCA中, 則表示當被試

n

掌握題目

i

考查的任意第

k

個屬性時, 其理想正確作答概率就是1。Maris (1995, 1999)認為分離縮合規(guī)則反映出題目允許被試采用多策略(利用不同的屬性或屬性組合)來解答。因此, DINO適合測量一些非能力心理特質(Templin & Henson, 2006)且在診斷被試作答錯誤原因方面也很有優(yōu)勢。與 DINO對應,則RPa-DINO可被描述為：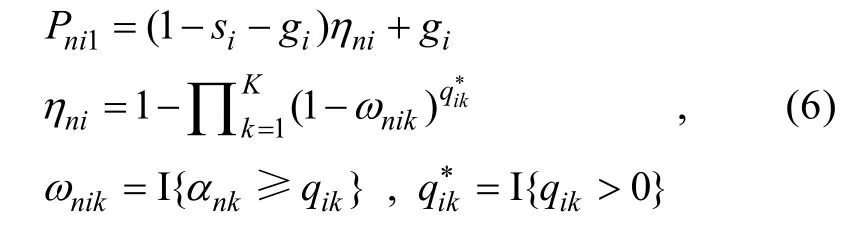

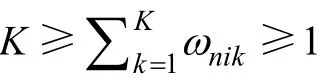
2.4 RPa-LLM簡介

Maris (1999)借鑒 Muthén (1978)、Bock 和 Aitkin(1981)的題目因素分析模型的思想, 指出補償模型(compensatory model)的背后假設是當題目考查多個潛變量時, 被試對各潛變量的掌握程度能夠相互彌補。則補償縮合規(guī)則可被描述為：

式中各參數含義同上, 其表示

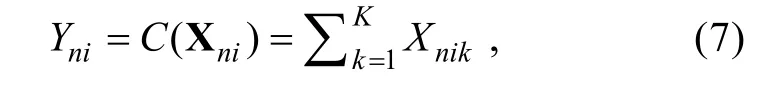
Y

等于

K

個

X

之和。應用至DCA中, 是指被試

n

對題目

i

的正確作答概率(的對數發(fā)生比)會隨著被試掌握該題目所考查的屬性個數的增加而增加。因此, LLM適合測量言語類能力, 因為通常認為言語類能力之間是可以相互補償的(Bernhardt, 2010; Stanovich, 2000)。關于 LLM 的介紹可參閱 Maris (1999)和詹沛達等(2015), 不再贅述。則RPa-LLM可被描述為：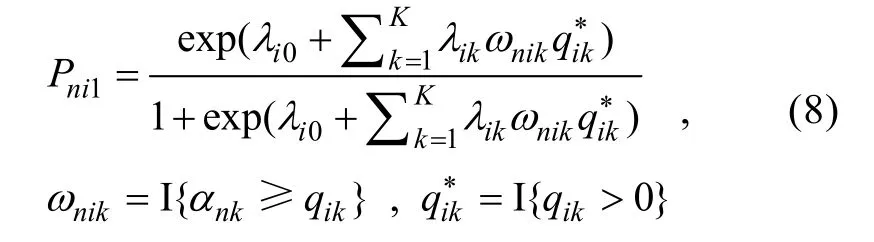

式中,

λ

為題目

i

的截距, exp (

λ

)/[1+exp (

λ

)]用于描述正確作答題目

i

的基線概率;

λ

為題目

i

中屬性

k

的權重(即

λ

≥0), 用于描述掌握屬性

k

對正確作答題目

i

的概率的對數發(fā)生比的增量; 其他參數含義同上。同樣, 當

L

= 1時式(8)就可直接用于描述LLM, 無需做任何形式上的改變, 這符合“LLM 應是RPa-LLM的約束模型”這一基本邏輯。

3 實驗設計

3.1 研究內容及自變量設定

本研究涉及6個潛在影響因素：多分屬性的數量(

K

= 3, 5, 7)、多分屬性的最高水平數(

L

= 2, 3, 4,5)、各多分屬性之間相關性(

Cor =

零相關(0)

、

低相關(0.2)、中等相關(0.5)和高相關(0.8))、多分屬性間的層級結構(

H

= 離散型、線型、發(fā)散型、聚合型, 見圖2 (Sun et al., 2013))、被試量(

N

= 500、1000、2000)和題目數(

I

= 25、50)。

為便于清晰地探究各潛在影響因素, 本文包含兩個研究, 其中：研究1側重于探討前4個主要自變量對RPa-DCMs的獨立影響, 包括4個子研究(1)多分屬性數量對RPa-DCMs的判準率影響; (2)多分屬性的最高水平數對RPa-DCMs的判準率影響; (3)多分屬性間的相關性對 RPa-DCMs的判準率影響;(4)多分屬性層級結構對 RPa-DCMs的判準率影響;而實際測驗中應存在多自變量的共同影響, 研究 2就側重于探討多個自變量對 RPa-DCMs的判準率的共同影響。以期為實證研究者提供相關理論支持。

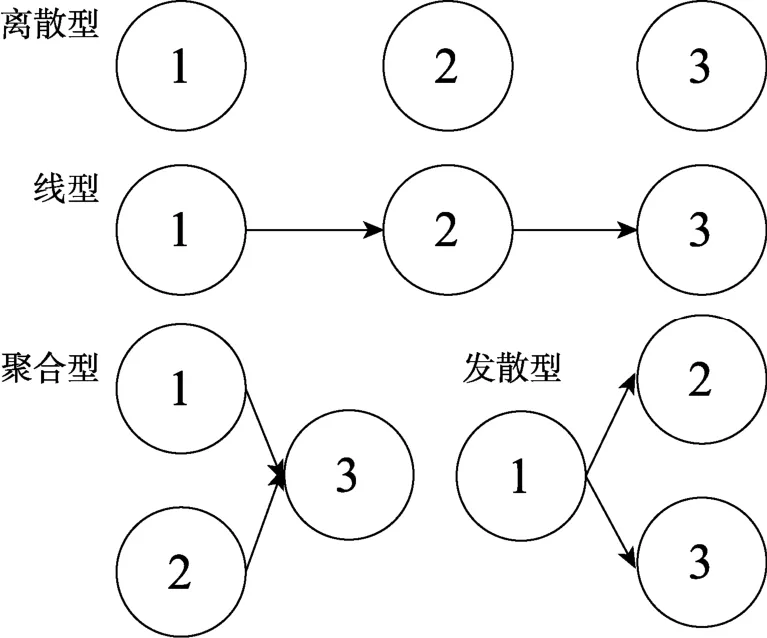
圖2 多分屬性之間的層級結構示例

3.2 評價指標

采用屬性判準率

ACCR

和屬性模式判準率

PCCR

作為屬性返真性的評價指標：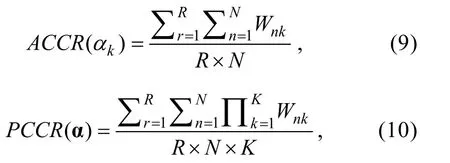

式中,

N

為樣本容量,

K

為屬性個數,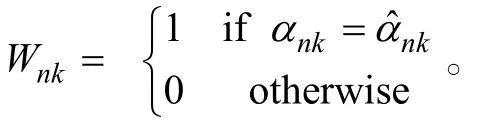

3.3 測驗Qp矩陣的建構

基于多分認知屬性層級結構建構多分可達矩陣(polytomous reachability matrix, R), 之后根據擴張算法即可得到簡化 Q矩陣, 具體操作方法可參見Sun等(2013)和丁樹良等(2015)。以圖 2中3個多分屬性(離散型/

L

= 2)為例, 則其對應的R矩陣和簡化Q矩陣見表1, 其余情況讀者可自行推算。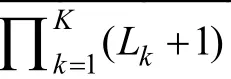

表1 3個多分屬性(離散型/L = 2)的Rp矩陣和簡化Qp矩陣

3.4 被試屬性掌握狀態(tài)

當不考慮屬性層級結構時(離散型), 被試屬性掌握狀態(tài)采用如下方法生成：(1)依據多元正態(tài)分布

MVN

(0, Σ)生成

K

維連續(xù)變量矩陣; (2)設定各連續(xù)變量滿足標準正態(tài)分布, 則對其按Z值表進行面積均等的(

L

+1)段切割(e.g.,

L

= 2時, 就按?0.44和0.44進行3段切割); (3)通過設定Σ矩陣來調控各多分屬性之間的相關。當考慮屬性層級結構時(發(fā)散型、聚合型、線型), 被試屬性掌握狀態(tài)在簡化 Q矩陣(增加全 0模式)中隨機抽取, 且盡量保持每種掌握每種屬性模式的被試數量相等。

3.5 模擬作答

模擬作答時, 首先根據各參數“真值”和RPa-DCMs計算被試

n

在項目

i

上的正確作答概率

P

。其次生成一個隨機數

r

(0≤

r

≤1), 則得 1分的條件為：

3.6 參數估計

本文采用基于貝葉斯MCMC算法的OpenBUGS(Spiegelhalter, Thomas, Best, & Lunn, 2014)進行參數估計, OpenBUGS代碼可向第一作者索取。另外,讀者若使用Chen和de la Torre (2013)的pG-DINA模型, 可直接使用R軟件中的CDM包來實現更為快速的參數估計。作者已驗證, 使用RPa-DCMs與直接使用 pG-DINA的約束模型去擬合同一批數據可得到相同的參數估計結果, 包括屬性(模式)估計值和需要相互轉化的題目參數。

4 研究1：4個主要自變量對RPa-DCMs判準率的獨立影響

4.1 多分屬性數量對RPa-DCMs的判準率影響

4.1.1 研究目的與基本參數設定

在二分屬性情境下已經有大量研究表明DCMs的判準率隨被考查屬性數量的增加而降低(e.g., de la Torre, 2009; 涂冬波, 蔡艷, 戴海琦, 2013; 蔡艷, 涂冬波, 丁樹良, 2013; 詹沛達, 王立君, 陳飛鵬,2013)。那么在多分屬性情境下是否會有同樣的結論？研究1就針對該問題進行探討, 未避免其余變量對結果的影響, 將它們固定為：

L

= 2,

Cor

= 0,

H

= 離散型,

N

= 2000,

I

= 50, 在相同實驗條件下3個RPa-DCMs采用相同的測驗 Q矩陣, 相同的被試掌握屬性狀態(tài)。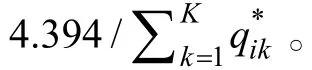

4.1.2 研究結果與結論

研究結果見表 2, 低于 0.6的結果已用粗體標出, 下同。針對 RPa-DINA, 當多分屬性個數為 3時, 均ACCR為0.969, PCCR為0.921; 當多分屬性數量提高到 5時, 均 ACCR降為 0.926, 而 PCCR的降幅達0.2左右; 當多分屬性數量提高到7個時,均ACCR已降至0.9以下, PCCR僅為0.555, 已經不足以滿足實際測驗需要。與 RPa-DINA類似,RPa-DINO和RPa-LLM的均ACCR和PCCR也隨著多分屬性數量的增加而降低。且RPa-LLM受多分屬性個數的影響相對更大, 這可能與 RPa-LLM的縮合規(guī)則需要更多的信息量有關。

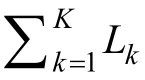
4.2 多分屬性的最高水平數對RPa-DCMs的判準率影響

4.2.1 研究目的與基本參數設定

多分屬性與二分屬性的最大區(qū)別就是屬性的水平數差異, 多分屬性比二分屬性的劃分更為精細,理論上可提供更多、更精細的診斷信息。但正如上文所述, 隨著屬性被劃分為更多的水平, 其可能的屬性模式數將大幅提升, 可能會對判準率帶來一定影響, 那么在具體應用中把最高水平設定為多少是合適的呢？研究2就針對該問題進行探討, 為避免其余變量對結果的影響, 將它們固定為：

K

= 3,

Cor

=0,

H

= 離散型,

N

= 2000,

I

= 50, 在相同實驗條件下3個RPa-DCMs采用相同的測驗Q矩陣, 相同的被試掌握屬性狀態(tài)。題目參數設定同研究1一致。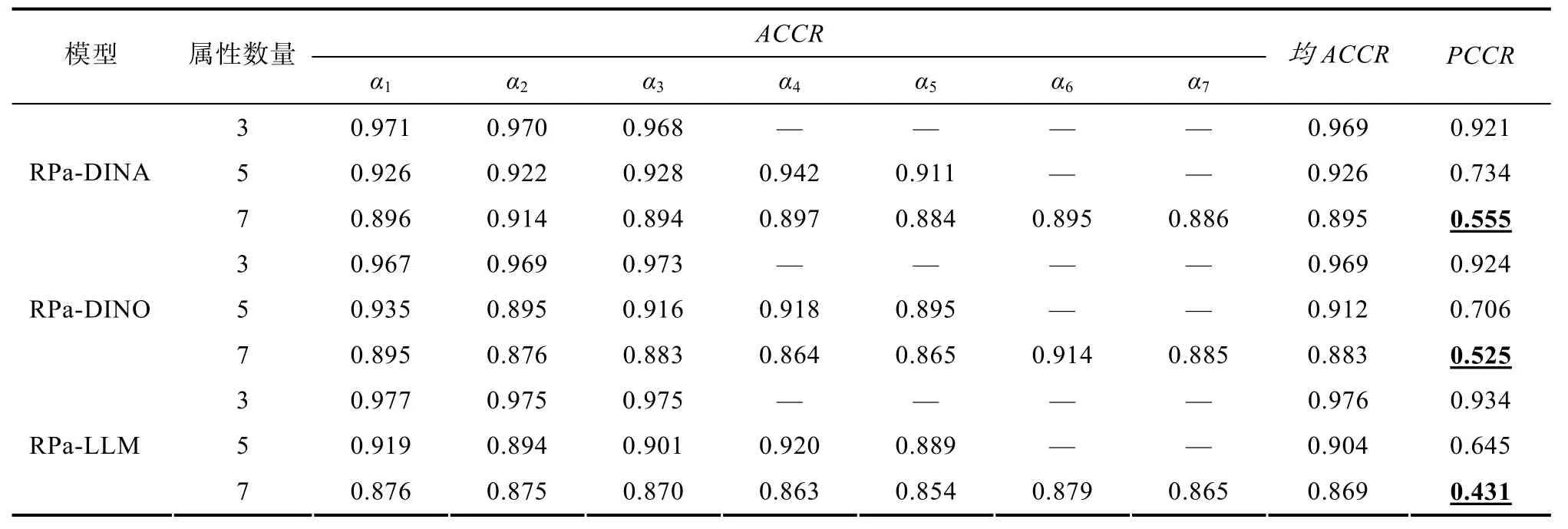

表2 不同多分屬性數量時RPa-DCMs的判準率

4.2.2 研究結果與結論

研究結果見表 3。當多分屬性最高水平數為 2時, 3個RPa-DCMs的均ACCR和PCCR基本相等且較高; 當最高水平數達到 5時, RPa-DINA和RPa-DINO的PCCR降至0.7左右, 而RPa-LLM的降至0.6左右。隨著最高水平數的提升, RPa-DINA和RPa-DINO的均ACCR和PCCR出現等幅下降,而 RPa-LLM 的下降趨勢相對較大。另外, 相比于多分屬性數量的提升, 最高水平數提升時的降幅較小。此外, 我們還計算了各水平的判準率, 基本結果趨勢與整體相當且各水平的判準率基本一致, 限于篇幅原因未呈現。

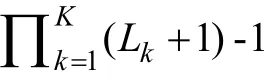
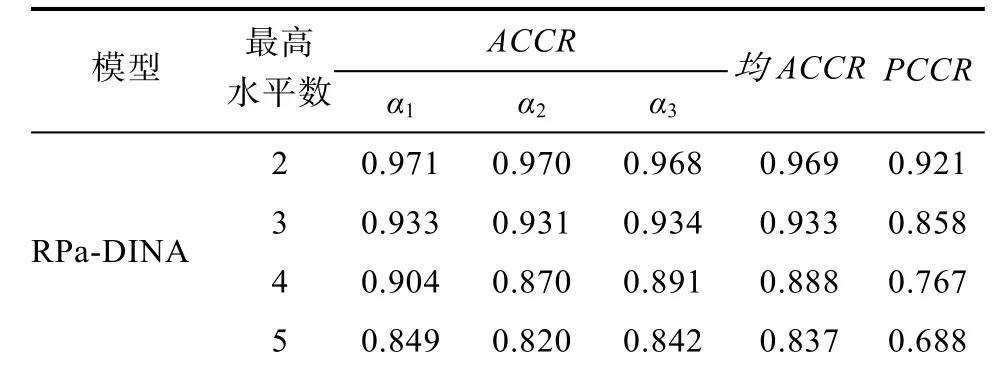
表3 不同多分屬性最高水平數時RPa-DCMs的判準率

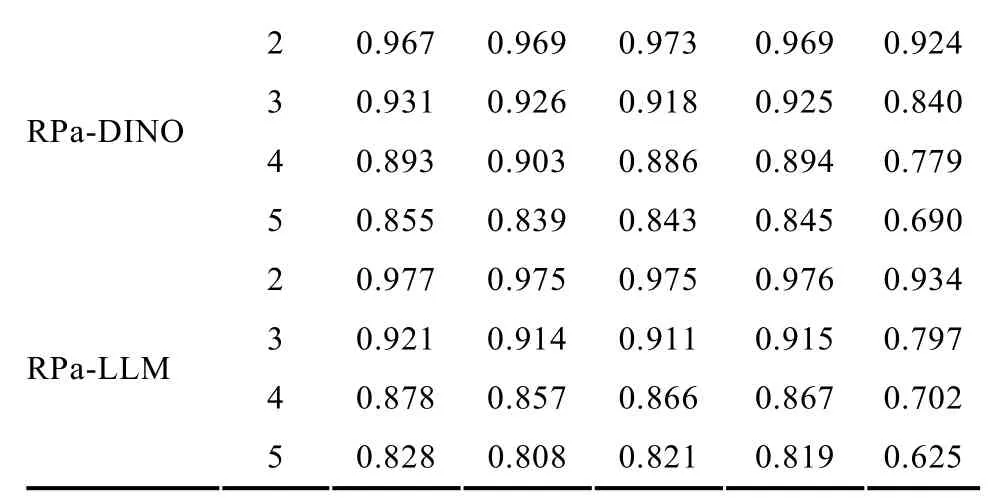
RPa-DINO 2 0.967 0.969 0.973 0.969 0.924 3 0.931 0.926 0.918 0.925 0.840 4 0.893 0.903 0.886 0.894 0.779 RPa-LLM 5 0.855 0.839 0.843 0.845 0.690 2 0.977 0.975 0.975 0.976 0.934 3 0.921 0.914 0.911 0.915 0.797 4 0.878 0.857 0.866 0.867 0.702 5 0.828 0.808 0.821 0.819 0.625

4.3 多分屬性間的相關性對RPa-DCMs的判準率影響

4.3.1 研究目的與基本參數設定

以往關于 DCMs的模擬研究大都假設屬性之間是零相關或忽視了生成屬性之間的相關性(e.g.,涂冬波等, 2013; 蔡艷等, 2013; Chen & de la Torre,2013; 詹沛達等, 2015), 但大量實證研究表明屬性之間通常是存在相關性的。那么, DCMs的判準率會不會受到屬性間相關性的影響？基于零相關假設或忽視了生成屬性間相關情境下得到的研究結論是否存在局限性？對此, 本研究將探討多分屬性間的相關性對RPa-DCMs判準率的影響, 為避免其余變量對結果的影響, 將它們固定為：

K

= 3,

L

= 2,

H

= 離散型,

N

= 2000,

I

= 50, 在相同實驗條件下3個 RPa-DCMs采用相同的測驗 Q矩陣, 相同的被試掌握屬性狀態(tài)。題目參數設定同研究1一致。

4.3.2 研究結果與結論

研究結果見表 4。發(fā)現, 3個 RPa-DCMs的均ACCR和PCCR均隨著多分屬性間的相關性提升而提升, 盡管幅度不大。增幅最大處在中等相關到高相關這一階段。該結果表明, 盡管以往研究在生成屬性時存在零相關假設或忽視了屬性間的相關性,但它們得到的結論仍對實證研究具有指導意義。

總之, RPa-DCMs的判準率隨多分屬性之間的相關性的增加而增加。當然, 在實際測驗中測驗編制者是很難操控該自變量, 但至少本研究表明：當實證研究中屬性間存在一定程度相關, 對判準率來講并非壞事。另外, 作者認為屬性層級結構(Leighton,Gierl, & Hunka, 2004)與屬性之間相關性至少在概念上是可以相互獨立的, 屬性層級結構描繪的是屬性之間的邏輯關系, 是測驗編制者可以操控的, 而屬性之間相關性是一個一定程度上依附于抽樣群體的統計值, 測驗編制者難以操控。同樣的屬性層級結構會隨著抽樣群體的不同而得到不同的屬性間相關性, 類似, 同樣的屬性間相關性也可能存在于不同的屬性層級結構之中。

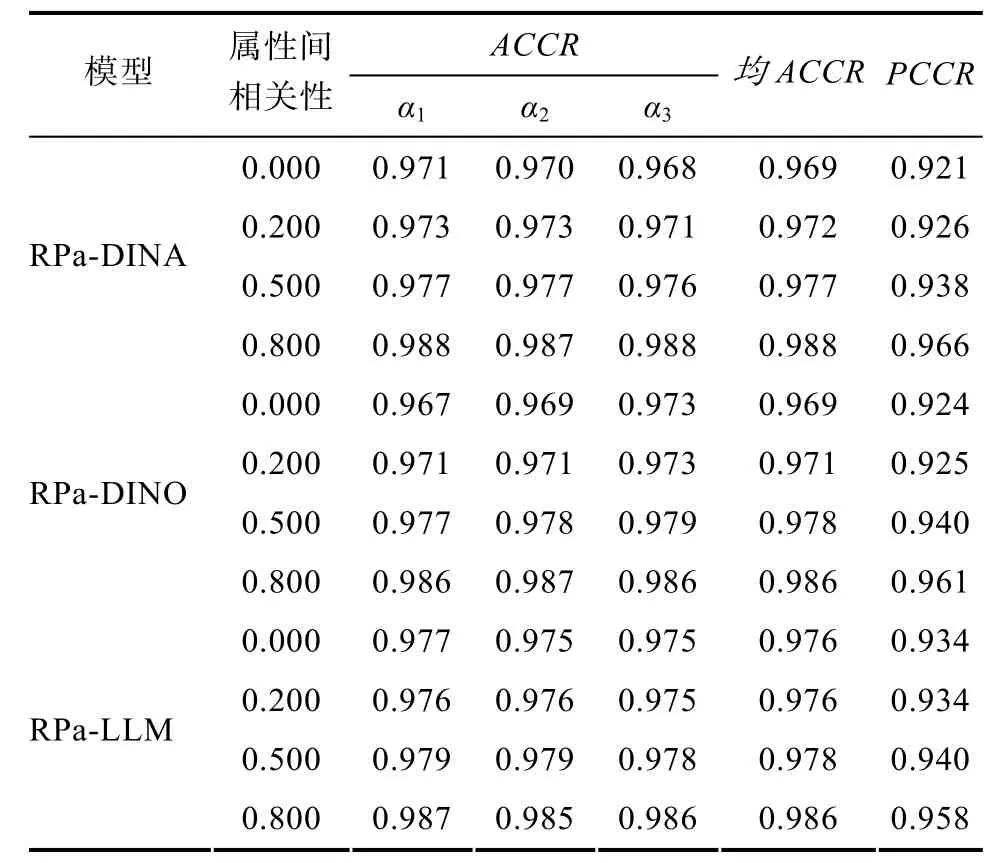
表4 多分屬性間不同的相關性時RPa-DCMs的判準率

4.4 多分屬性層級結構對RPa-DCMs的判準率影響

4.4.1 研究目的與基本參數設定

在二分屬性情境下, 涂冬波等(2013)和蔡艷等(2013)曾探討了5種假設屬性間滿足連接縮合規(guī)則的診斷分類方法在不同屬性層級結構下的表現, 他們建議當無法確定屬性層級結構是否正確時應使用DINA, 即DINA受屬性層級結構的影響相對較小。詹沛達等(2013)也曾探討了假設屬性間滿足分離縮合規(guī)則的DINO對屬性層級結構的敏感性, 其結果表明DINO更適用于處理離散型屬性關系的數據, 而在線型、發(fā)散型和聚合型層級結構中表現較差。那么這些結論在多分屬性情境下是否同樣適用？本研究將針對該問題進行探討, 多分屬性層級結構(見圖 2)及多分屬性個數(

K

= 3)參見 Sun等(2013)一文, 為避免其余變量對結果的影響, 將它們固定為：

L

= 3,

Cor

= 0,

N

= 2000,

I

= 50, 在相同實驗條件下3個RPa-DCMs采用相同的測驗Q矩陣, 相同的被試掌握屬性狀態(tài)。題目參數設定同研究1一致。

4.4.2 研究結果與結論

研究結果的具體數值見表 5。盡管 3個RPa-DCMs其自身均不考慮屬性層級結構(i.e., 所有屬性模式均納入參數估計), 但它們的判準率還是會受到屬性層級結構的影響。其中, RPa-DINA受屬性層級結構的影響最小。而RPa-DINO對屬性層級結構最敏感, 無論是聚合型、發(fā)散型還是線型,其均ACCR和PCCR均是最低的, 尤其是在線型和聚合型中, 屬性 3的判準率已經降到 0.25和 0.35左右了, 已失去可用性。因此, RPa-DINO僅適用于多分屬性間滿足離散關系的測驗情境中, 這也驗證了詹沛達等(2013)在二分屬性情境下得到的結論。再有, RPa-LLM對屬性層級結構也較為敏感, 判準率處于 RPa-DINA和 RPa-DINO之間, 盡管其PCCR保持在 0.6以上, 但實際使用中還是建議使用在屬性之間滿足離散關系的測驗情境中。另外,還可發(fā)現當屬性間存在層級結構時, 子屬性的判準率會低于其父屬性的判準率, 以線型為例, 從

α

到

α

再到

α

, 其ACCR依次降低, 發(fā)散型和聚合型也有類似的結果。最后需要說明的是, 如果在數據分析前能確保測驗Q矩陣或屬性層級結構是正確的,則可以將不符合層級結構的屬性模式在參數估計時刪除。屬性的最高水平數增加而降低, 建議實際使用中不超過4水平; (3)隨多分屬性間的相關性增加而增加,且對判準率的影響相對較小; (5)會受到多分屬性層級結構的影響, 其中 RPa-DINA受影響最小,RPa-LLM居中, RPa-DINO受影響最大, 建議實際使用RPa-DINO和RPa-LLM分析數據前, 要確定屬性間是否存在潛在的層級結構。

根據研究1中4個子研究的結果, 將結論整理如下：RPa-DCMs的判準率(1)隨多分屬性數量的增加而降低, 建議實際使用中不超過5個; (2)隨多分

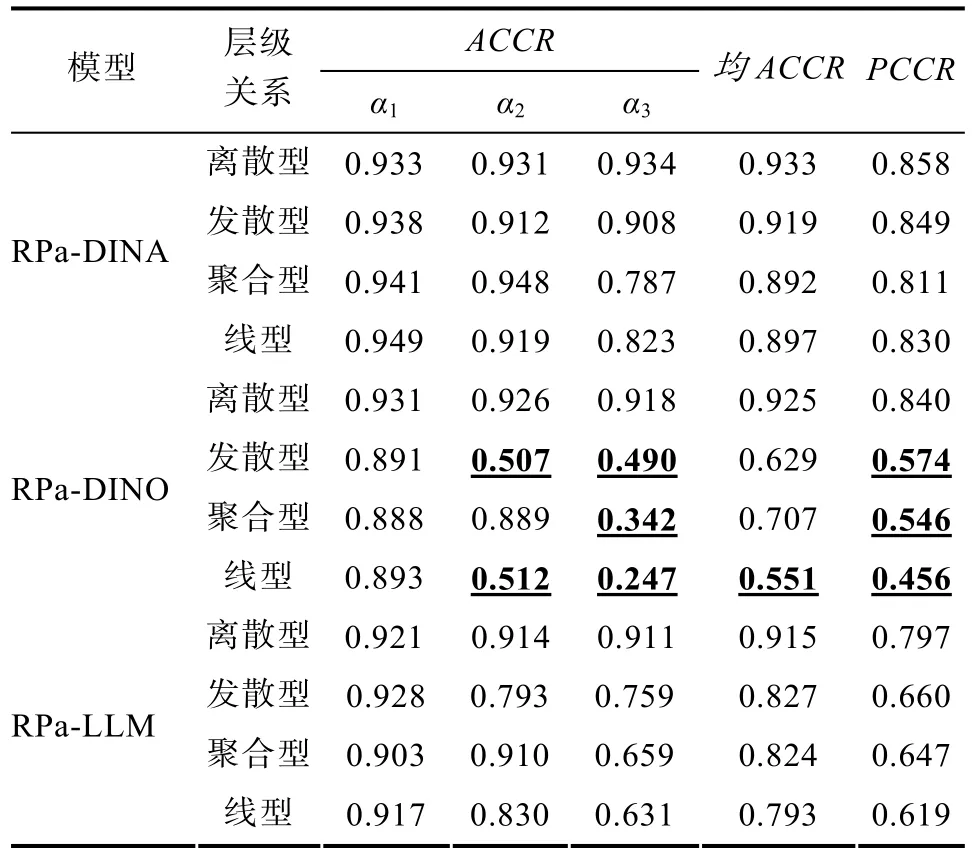
表5 不同屬性層級結構下RPa-DCMs的判準率

5 研究2：RPa-DCMs判準率的影響的多因素設計模擬研究

5.1 研究目的與基本參數設定

根據已有研究結果(e.g., de la Torre, Hong, &Deng, 2010; Chen & de la Torre, 2013; 蔡艷等, 2013;詹沛達等, 2015)可知, 足夠的被試量和題目數是模型實現準確和穩(wěn)定參數估計結果的必要前提, 通常越復雜的模型對被試量和題目數的要求越高。研究1在探討多分屬性數量、屬性最高水平數、屬性間相關性和屬性層級結構這4個主要自變量時, 將被試量與題目數固定在一個較充足的條件下, 而實際測驗很有可能無法保證足夠的被試量與題目數, 則此時RPa-DCMs的表現又如何？另外, 根據研究1的結論可知屬性間相關性對判準率的影響不大且在離散型層級結構下探討 RPa-DINO和 RPa-LLM才有意義, 因此研究2中將這兩個自變量進行固定(

Cor

= 0,

H

= 離散型), 僅探討被試量、題目數、多分屬性數量與最高水平數這4個自變量同時存在時3個RPa-DCMs的判準率表現。

圖3 多個自變量同時存在對RPa-DINA判準率影響

5.2 研究結果與結論

研究2結果見圖3至圖5, 每個模型下均有24種實驗條件。其中一些結果驗證了研究1中的結論：

圖4 多個自變量同時存在對RPa-DINO判準率影響

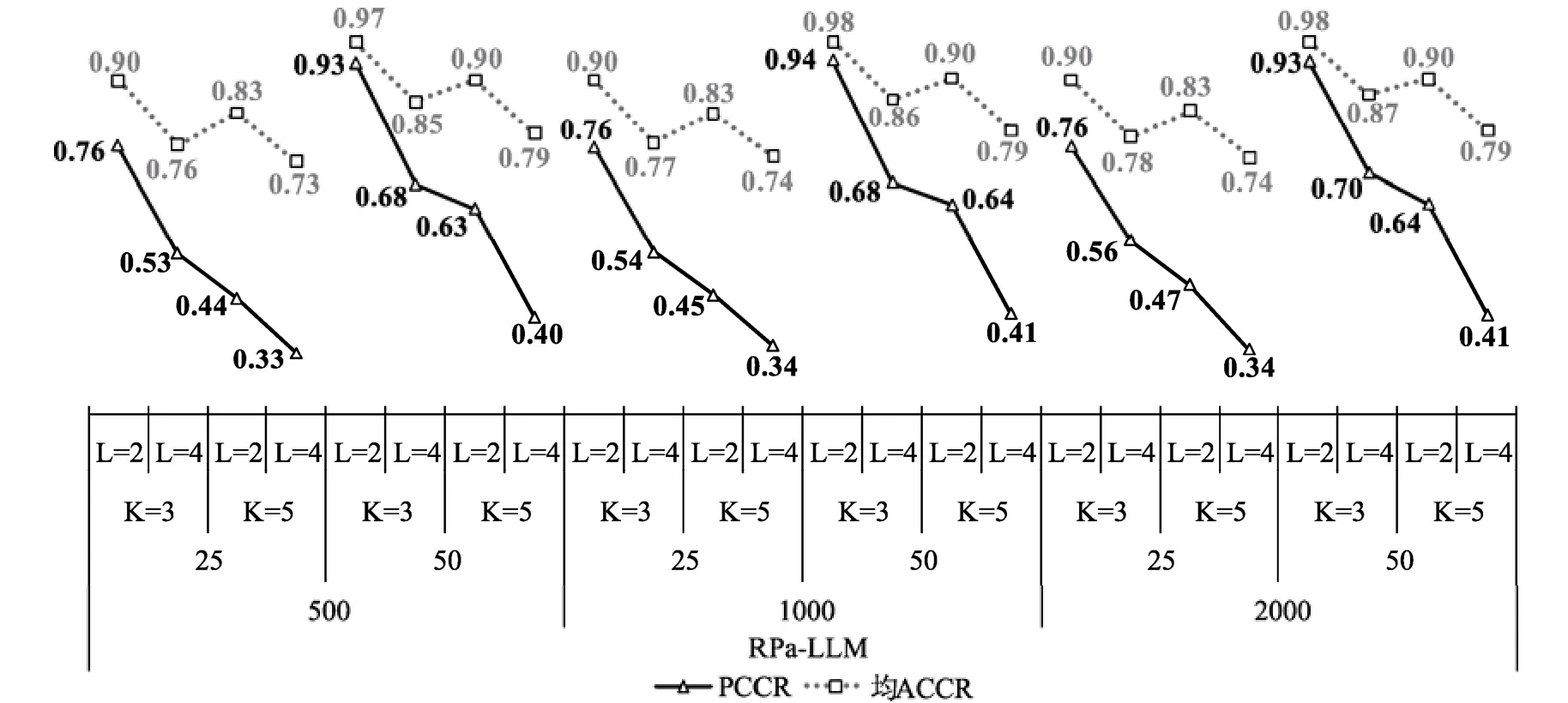
圖5 多個自變量同時存在對RPa-LLM判準率影響

當固定被試量和題目數后, 判準率隨屬性數量和屬性最高水平數的增加而降低, 且當兩者同時存在時,對判準率的影響更大(e.g.,

K

= 5/

L

= 4比

K

= 3/

L

=2的判準率低0.5左右)。另外還可發(fā)現, 增加題目數可促進判準率增加且影響相對較大, 而被試量對判準率幾乎無影響。這與二分屬性情境下的研究結論類似(e.g., 蔡艷等, 2013; 詹沛達等, 2015), 另外結合de la Torre等(2010)和詹沛達等(2015)的研究結果可知被試量主要影響的是題目參數的返真性,而題目數則影響被試參數(i.e., 屬性或能力)的返真性。如若實際測驗中更關注的是判準率, 而對題目參數返真性的要求沒有那么高, 那么在使用RPa-DCMs時首先要保證的是有充足的題目數, 以減少對被試的診斷信息出現誤導的可能。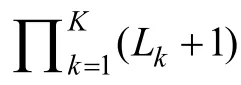

6 討論與總結

6.1 討論

6.1.1 多分屬性與多級評分之間的關系

觀察3個RPa-DCMs后, 很容易發(fā)現盡管它們考慮到了屬性的多水平劃分, 但它們仍是二級評分(dichotomous scoring)DCMs。目前, 在DCA中盡管已有一些研究在探討如何實現多級評分, 但還缺乏一個被普遍認可的方法。大體可將現有的多級評分方法分為兩類：屬性與分數相對應法(e.g., 祝玉芳,丁樹良, 2009; 田偉, 辛濤, 2012; Sun et al., 2013)和屬性與分數相獨立法(e.g., Templin, Henson, Rupp,Jang, & Ahmed, 2008; Hansen, 2013; 涂冬波等,2010)。其中, 前者是指非純心理測量模型診斷法(e.g., RSM (Tatsuoka, 1983, 1985)、AHM (Leighton et al., 2004))特有的一種需要滿足一系列假設的評分方法。假設依次為(1)“屬性外顯假設”：評分者能夠根據被試的作答(當被試未給出某題的正確答案時, 評分者能夠根據現有的答案(或作答流程))判斷出被試可能掌握了哪些屬性及對這些屬性掌握水平; (2)“屬性與分數相對應假設”：被試得分等于被試正確作答的題目所考察的屬性最高水平數加權之和, 可被描述為：

式中,

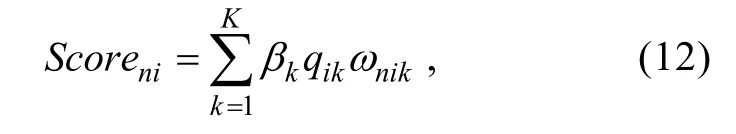
Score

表示被試

n

在題目

i

上的得分,

β

表示屬性

k

的得分加權,

q

為Q矩陣中的元素,

ω

為潛在作答。當各屬性權重相等(

β

=

β

)時, 式(12)退化為多分屬性情境下的屬性與分數相對應評分方法(e.g., Sun et al., 2013)。進一步當

β

=

β

且

L

= 1時, 式(12)就退化為二分屬性情境下的屬性與分數相對應評分方法(e.g., 祝玉芳, 丁樹良, 2009; 田偉,辛濤, 2012); (3)“屬性間滿足連接縮合規(guī)則假設”：由式(12)知, 該評分方法其實是一個潛在作答的累加過程, 僅當被試所有的潛在作答均為1時才能累加得到滿分, 因此各屬性之間必須滿足連接縮合規(guī)則。而這3個假設的存在會大大限制屬性與分數相對應法的適用范圍, 比如：不適用于多項選擇題(multiple-choice item) (因為選項數量的限制, 當屬性(水平)數量之和大于選項數量時, 則分數與屬性(數量)之間的關系無法被合適地描述); 另外, 當建構反應題(constructed response item)的評分細則中的采分點與屬性不對應時, 該方法也無法使用。

與之不同, 屬性與分數相獨立法則是源自于IRT 中的多級評分方法(e.g., 等級反應(graded response)、部分評分(partial credit)、稱名反應(nomial response)等), 該方法認為評分與潛質(i.e.,屬性或能力)是兩個相互獨立的概念, 即評分方法僅涉及題目參數的而與被試參數無關。單維(相當于 1道題目僅考查 1個屬性)題目亦可以有多級評分, 同理, 題目內多維(相當于1道題目考查多個屬性)題目亦可僅有二級評分, 即“多維度不等于多級評分”。該方法不存在與屬性與分數相對應法相類似的強假設, 適用范圍更廣泛(e.g., 多項選擇題、建構反應題等)。在二分屬性情境下, Hansen (2013)在LCDM (Henson et al., 2009)的基礎上使用等級反應評分法提出了等級反應LCDM。Templin等(2008)在LCDM (Henson et al., 2009)的基礎上使用稱名反應評分法提出了稱名反應診斷模型。這兩個模型可被視為是屬性與分數相獨立評分法的代表。

綜上所述, 當多級評分采用屬性與分數相對應法時, 多級評分將依賴于多分屬性的水平數; 而當采用屬性與分數相獨立法時, 多分屬性與多級評分也是相獨立的, 本研究評分方式為屬性與分數相獨立法, 相應的多級評分RPa-DCMs已另攥文闡述。

6.1.2 多分屬性與二分屬性之間的關系

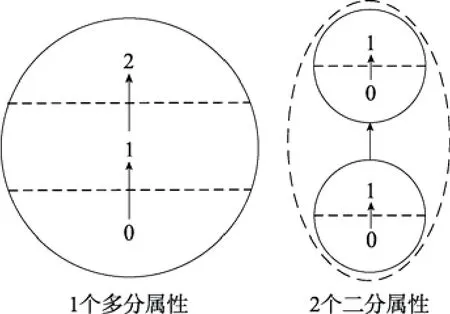
圖6 多分屬性與二分屬性對應關系示例

丁樹良等(2015)也使用膨脹算法探討了如何將R矩陣轉化為與之相對應的二分矩陣(稱之為M矩陣), 從中也能得出與Karelitz (2004)相同的結論。以圖1中聚合型層級結構為例, 假設3個多分屬性的

L

= 2, 即

a

∈{0,1,2}, 則其對應的R矩陣以及相對應的M矩陣為：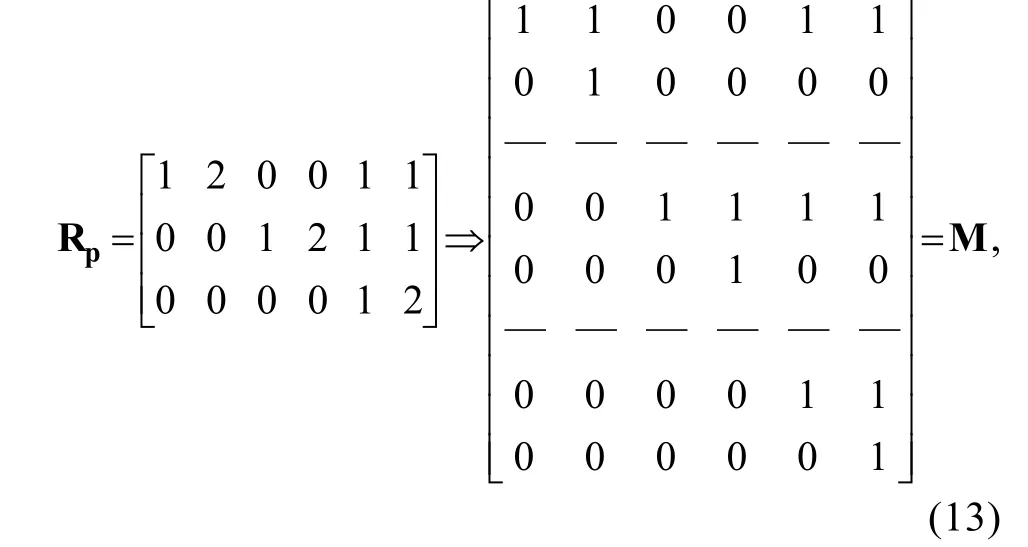

為了讓讀者更好地理解多分屬性與二分屬性之間的關系, 我們結合 Karelitz (2004)和丁樹良等(2015)的研究, 以線型和聚合型為例把多分屬性(

L

=2)和二分屬性的之間的對應關系以圖式表示出來,見圖 7, 其中二分屬性中的“1-1”和“1-2”是指由多分屬性“1”拆分而來的(見圖 6), 其余屬性同理。仍以聚合型為例, 經推算圖7中右側6個二分屬性的可達矩陣, 可得到式(13)中的 M 矩陣, 同時經推算圖7左邊的3個多分屬性的可達矩陣, 可得到式(13)中的R矩陣。同時可發(fā)現, 當假設3個多分屬性之間存在層級結構時, 其對應的二分屬性之間的層級結構僅存在于屬性“1-1”、“2-1”和“3-1”之間, 而“1-2”、“2-2”和“3-2”之間相互獨立。同理可知, 無論多分屬性的最高水平數

L

多大, 各屬性之間的層級結構僅建構在第1和第2水平(i.e., 0和1)上。另外根據上述內容也可推知, 當把多分屬性轉換為與之對等的二分屬性后, 其可能是潛在屬性模式(或待估計屬性模式參數)數量仍保持不變。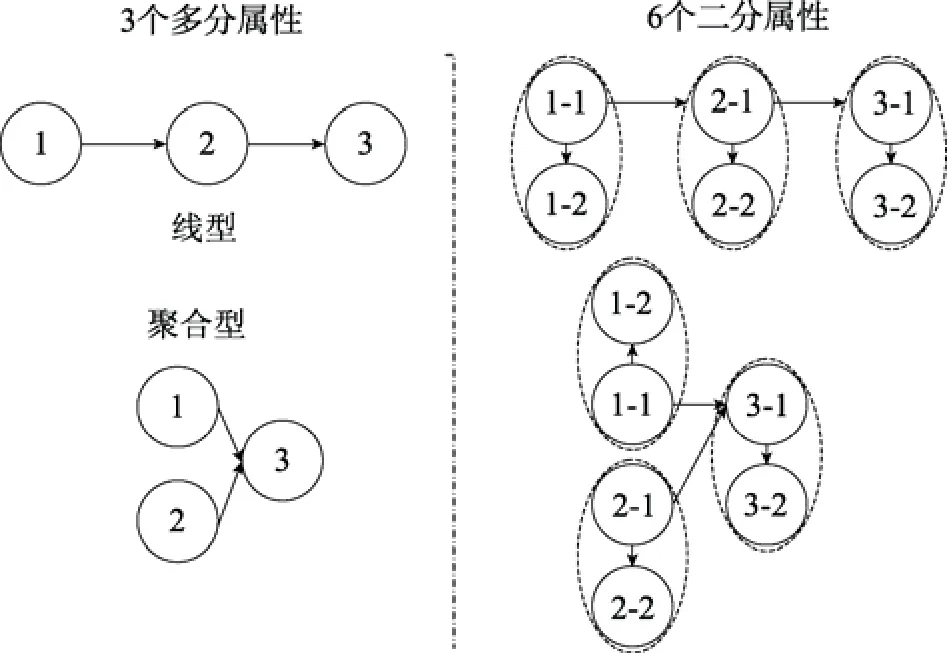

圖7 線型與聚合型層級結構下多分屬性與二分屬性的對應關系

6.2 總結

由于多分屬性將被試對屬性的掌握情況進行了更為細致的劃分, 所以它比二分屬性提供更多地診斷反饋信息, 也更符合當前國家教育政策(e.g.,《全日制義務教育數學課程標準(修改稿)》)中對知識技能的多水平要求, 具有較好的應用前景。本文首先介紹了多分屬性和多分 Q 矩陣的概念; 之后重參數化了3個分別滿足連接、分離和補償縮合規(guī)則的RPa-DCMs表達式, 以期簡化讀者對Pa-DCMs理解;然后, 我們探討了多分屬性數量、多分屬性最高水平數、多分屬性之間的相關性、多分屬性層級結構、被試量和題目數對3個RPa-DCMs判準率的影響,根據研究結果發(fā)現：(1)RPa-DCMs的判準率隨多分屬性數量的增加而降低, 受影響程度從大到小依次為RPa-LLM、RPa-DINO和RPa-DINA。當多分屬性的最高水平數較低且題目數量充足時, 多分屬性數量也不宜超過5個; (2)判準率隨多分屬性最高水平數的增加而降低, 其中 RPa-LLM 受影響程度相對最大, 而RPa-DINA和RPa-DINO受影響程度類似。當多分屬性的最高水平數較低且題目數量充足時, 多分屬性的最高水平數不宜超過 4; (3)判準率隨多分屬性之間的相關性的增加而增加, 但影響程度相對較小, 實際測驗中可不用考慮該因素對判準率的影響; (4)多分屬性間的層級結構對不同模型的影響不同, 受影響程度從大到小依次為RPa-DINO、RPa-LLM和RPa-DINA。建議實際使用RPa-DINO和 RPa-LLM 分析數據前, 要確定屬性間是否存在潛在的層級結構; (5)被試量對判準率影響很小, 若實際測驗中更關注的是判準率而非題目參數的返真性, 則尋找較小的樣本量即可滿足測驗需求; (6)題目數對判準率的影響很大, 當題目數量從較少(25題)提升到中等(50題)時, 3個RPa-DCMs的判準率均有 10%～20%左右的提升。因此實際測驗中充足的題目數是得到準確、有效診斷結果的必要前提之一。最后, 本文還探討了“多分屬性與多級評分之間的關系”和“多分屬性與二分屬性之間的關系”這兩個的問題。以期為實證研究者提供相關的理論支持與使用建議。

當然, 由于精力和篇幅有限且為聚焦研究主題,本文對部分研究條件做了簡化或限定：(1) Q矩陣界定正確; (2)多分屬性層級結構界定正確; (3)題目參數固定; (4)各屬性考查次數均衡; (5)限于二級評分數據等等, 而這些限定的研究條件也均可能是RPa-DCMs判準率的影響因素, 值得今后研究進一步探討。

Bernhardt, E. B. (2010).

Understanding advanced secondlanguage reading

. New York: Routledge.Bock, R. D., & Aitkin, M. (1981). Marginal maximum likelihood estimation of item parameters: Application of an EM algorithm.

Psychometrika, 46

, 443–459.Cai, Y., Tu, D. B., & Ding, S. L. (2013). A simulation study to compare five cognitive diagnostic models.

Acta Psychologica Sinica,45

, 1295–1304.[蔡艷, 涂冬波, 丁樹良. (2013). 五大認知診斷模型的診斷正確率比較及其影響因素: 基于分布形態(tài)、屬性數及樣本容量的比較.

心理學報, 45

, 1295–1304.]Chen, J. S., & de la Torre, J. (2013). A general cognitive diagnosis model for expert-defined polytomous attributes.

Applied Psychological Measurement, 37

, 419–437.de la Torre, J. (2008). An empirically based method of Q-matrix validation for the DINA model: development and applications.

Journal of Educational Measurement, 45

,343–362.de la Torre, J. (2009). DINA model and parameter estimation:A didactic.

Journal of Educational and Behavioral Statistics,34

, 115–130.de la Torre, J. (2011). The generalized DINA model framework.

Psychometrika, 76

, 179–199.de la Torre, J., & Douglas, J. A. (2004). Higher-order latent trait models for cognitive diagnosis.

Psychometrika, 69

, 333–353.de la Torre, J., Hong, Y., & Deng, W. L. (2010). Factors affecting the item parameter estimation and classification accuracy of the DINA model.

Journal of Educational Measurement, 47

, 227–249.Ding, S. L., Luo, F., Wang, W. Y., & Xiong, J. H. (2015). The properties of 0-1 and polytomous reach ability matrices and their applications.

Journal of Jiangxi Normal University(Natural Science Edition), 39

, 64–68.[丁樹良, 羅芬, 汪文義, 熊建華. (2015). 0-1和多值可達矩陣的性質及應用.

江西師范大學學報(自然科學版), 39

,64–68.]Ding, S. L., Wang, W. Y., & Yang, S. Q. (2011). The design of cognitive diagnostic test blueprints.

Journal of Psychological Science, 34

, 258–265.[丁樹良, 汪文義, 楊淑群. (2011). 認知診斷測驗藍圖的設計.

心理科學, 34

, 258–265.]Ding, S. L., Yang, S. Q., & Wang, W. Y. (2010). The importance of reachability matrix in constructing cognitively diagnostic testing.

Journal of Jiangxi Normal University (Natural Sciences Edition), 34

, 490–494.[丁樹良, 楊淑群, 汪文義. (2010). 可達矩陣在認知診斷測驗編制中的重要作用.

江西師范大學學報(自然科學版),34

, 490–494.]Embretson, S. (1984). A general latent trait model for response processes.

Psychometrika, 49

, 175–186.Hansen, M. P. (2013).

Hierarchical item response models for cognitive diagnosis

(Unpublished doctoral dissertation).University of California, LA.Huang, H. Y., & Wang, W. C. (2014). The random-effect DINA model.

Journal of Educational Measurement

,

51

,75–97.Henson, R. A., Templin, J. L., & Willse, J. T. (2009). Defining a family of cognitive diagnosis models using log-linear models with latent variables.

Psychometrika, 74

, 191–210.Junker, B. W., & Sijtsma, K. (2001). Cognitive assessment models with few assumptions, and connections with nonparametric item response theory.

Applied Psychological Measurement, 25

(3), 258–272.Karelitz, T. M. (2004).

Ordered category attribute coding framework for cognitive assessments

(Unpublished doctoral dissertation). University of Illinois at Urbana–Champaign.Leighton, J. P., Gierl, M. J., & Hunka, S. M. (2004). The attribute hierarchy method for cognitive assessment: A variation on Tatsuoka’s rule-space approach.

Journal of Educational Measurement, 41

, 205–237.Li, X. M., & Wang, W.-C. (2015). Assessment of differential item functioning under cognitive diagnosis models: The DINA model example.

Journal of Educational Measurement,52

, 28–54.Maris, E. (1995). Psychometric latent response models.

Psychometrika, 60

, 523–547.Maris, E. (1999). Estimating multiple classification latent class models.

Psychometrika, 64

, 187–212.Muthén, B. (1978). Contributions to factor analysis of dichotomous variables.

Psychometrika, 43

, 551–560.Rupp, A. A., Templin, J., & Henson, R. A. (2010).

Diagnostic measurement: Theory, methods, and applications

. New York: Guilford Press.Spiegelhalter, D., Thomas, A., Best, N., & Lunn, D. (2014).

OpenBUGS

User

Manual

Version

3.2.3

. URL:http://www.openbugs.net/Manuals/Manual.htmlStanovich, K. E. (2000).

Progress in understanding reading:Scientific foundations and new frontiers

. New York: The Guilford Press.Sun, J. N., Xin, T., Zhang, S. M., & de la Torre. (2013). A polytomous extension of the generalized distance discriminating method.

Applied Psychological Measurement,37

, 503–521.Tatsuoka, K. K. (1983). Rule Space: An approach for dealing with misconceptions based on item response theory.

Journal of Educational Measurement, 20

, 345–354.Tatsuoka, K. K. (1985). A probabilistic model for diagnosing misconceptions by the pattern classification approach.

Journal of Educational Statistics, 10

, 55–73.Templin, J. L., & Henson, R. A. (2006). Measurement of psychological disorders using cognitive diagnosis models.

Psychological Methods, 11

, 287–305.Templin, J. (2004).

Generalized linear mixed proficiency models for cognitive diagnosis

(Unpublished doctoral dissertation).University of Illinois at Urbana–Champaign.Templin, J., Henson, R., Rupp, A., Jang, E., & Ahmed, M.(2008).

Cognitive diagnosis models for nominal response data

. Paper presentation at the annual meeting of the National Council on Measurement in Education Society,New York, NY.Tian, W., & Xin, T. (2012). A polytomous extension of rule space method based on graded response model.

Acta Psychologica Sinica, 44

, 249–269.[田偉, 辛濤. (2012). 基于等級反應模型的規(guī)則空間方法.

心理學報, 44

, 249–269.]Tu, D. B., Cai, Y., & Dai, H. Q. (2013). Comparison and selection of five noncompensatory cognitive diagnosis models based on attribute hierarchy structure.

Acta Psychologica Sinica, 45

, 243–252.[涂冬波, 蔡艷, 戴海琦. (2013). 幾種常用非補償型認知診斷模型的比較與選用: 基于屬性層級關系的考量.

心理學報, 45

, 243–252.]Tu, D. B., Cai, Y., Dai, H. Q., & Ding, S. L. (2010). A polytomous cognitive diagnosis model: P-DINA model.

Acta Psychologica Sinica, 42

, 1011–1020.[涂冬波, 蔡艷, 戴海琦, 丁樹良. (2010). 一種多級評分的認知診斷模型: P-DINA模型的開發(fā).

心理學報, 42

,1011–1020.]von Davier, M. (2005).

A general diagnostic model applied to language testing data

(ETS Research Report no. RR-05-16).Princeton, NJ: Educational Testing Service.Whitely, S. E. (1980). Multicomponent latent trait models for ability tests.

Psychometrika, 45

, 479–494.Zhan, P. D., & Bian, Y. F. (2015). The probabilistic-inputs,noisy “and” gate model.

Journal of Psychological Science,38

, 1230–1238.[詹沛達, 邊玉芳. (2015). 概率性輸入, 噪音“與”門(PINA)模型.

心理科學, 38

, 1230–1238.]Zhan, P. D., Li, X. M., Wang, W.-C., Bian, Y.-F., & Wang, L. J.(2015). The multidimensional testlet-effect cognitive diagnostic models.

Acta Psychologica Sinica, 47

, 689–701.[詹沛達, 李曉敏, 王文中, 邊玉芳, 王立君. (2015). 多維題組效應認知診斷模型.

心理學報, 47

, 689–701.]Zhan, P. D., Wang, L. J., & Chen, F. P. (2013). Influence of various factors on the DINO's diagnostic accuracy.

Examinations Research,

(4), 60–67.[詹沛達, 王立君, 陳飛鵬. (2013). 不同因素對認知診斷DINO模型診斷準確率的影響.

考試研究,

(4), 60–67.]Zhu, Y. F., & Ding, S. L. (2009). A polytomous extension of attribute hierarchy method based on graded response model.

Acta Psychologica Sinica, 41

, 267–275.[祝玉芳, 丁樹良. (2009). 基于等級反應模型的屬性層級方法.

心理學報, 41

, 267–275.]