Logistic加權(quán)模型的理論構(gòu)建與模擬分析*

簡小珠 戴步云 戴海琦

(1井岡山大學(xué)教育學(xué)院, 江西 吉安 343009)

(2江西師范大學(xué)心理學(xué)院, 江西省心理與認(rèn)知科學(xué)重點實驗室, 南昌 330022)

1 前言

1.1 以往的多級記分模型

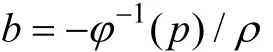
1.2 多級記分試題的試題屬性

多級記分試題的試題屬性主要表現(xiàn)為：(1)用試題滿分值來表達(dá)試題知識考查重要性程度的加權(quán)作用; (2)用平均得分比例來表達(dá)被試群體在多級記分試題上的平均難度。

第一個屬性：試題考查重要性程度加權(quán)作用。從測驗設(shè)計來看, 多級記分試題的賦分基本思想：給予某一道試題賦予更大的分?jǐn)?shù)權(quán)重, 是為了增大該試題在整份測驗中的分?jǐn)?shù)權(quán)重比例, 以反映所考查知識與能力的重要性。正如教學(xué)內(nèi)容、測驗內(nèi)容具有難點與重點, 試題也具有難易程度與考查重要性這兩個屬性。因此, 反映在IRT模型上應(yīng)使用不同的參數(shù)來表達(dá)多級記分試題的難度、重要性。試題難易程度是通過難度來體現(xiàn), 而試題所測量內(nèi)容的重要性則需通過分?jǐn)?shù)權(quán)重, 即權(quán)重參數(shù)來表達(dá)。試題所測量內(nèi)容重要性可通過該試題滿分值、或該試題所在內(nèi)容模塊總分在整份測驗總分的比重來體現(xiàn)。本文提出的Logistic加權(quán)模型將包含權(quán)重參數(shù)。

第二個屬性：試題的平均難度。被試群體在多級記分試題上的得分為：得1分及以上的人數(shù)比例最大, 得2分及以上的人數(shù)比例依次減小, 依此類推, 得滿分的被試人數(shù)比例最小。多級記分題的評分點結(jié)構(gòu)、評分等級相對復(fù)雜, 為簡化認(rèn)識, 可使用平均難度表達(dá)被試群體在多級記分試題上的得分比例, 也就是說, 計算被試群體在多級記分試題上的平均得分, 并除以該試題滿分值得到平均得分比例

P

, 即平均難度。

1.3 GRM在多級記分試題上應(yīng)用的不足

GRM在多級記分試題上應(yīng)用的不足：第一,GRM下多級記分試題的項目信息量并不是兩級記分試題的倍數(shù)。分別計算一道滿分為5分, 區(qū)分度為1, 難度參數(shù)分別為?1, ?0.5, 0.0, 0.5, 1的多級記分試題, 和一道區(qū)分度為1, 難度為0.0的兩級記分試題的項目信息量, 發(fā)現(xiàn)該多級記分試題的項目信息量在能力量尺的各個點上都僅僅比兩級記分試題多0.1～0.2。第二, GRM有時無法適合實際情境,(1)如果最后一個等級得分的被試太少, 會嚴(yán)重影響難度參數(shù)的估計(Embretson & Reise, 2000)。(2)評分為非連續(xù)時, 比如在英語測驗中詞匯題每題1分, 閱讀理解每題2分(答對給2分, 答錯給0分,無中間得分), 在GRM下無法進(jìn)行參數(shù)估計。

2 Logistic加權(quán)模型的構(gòu)建思想

2.1 Logistic加權(quán)模型的平均難度參數(shù)

以往GRM等多級記分模型是建立兩級記分Logistic模型的基礎(chǔ)上, 用

m

道不同難度的兩級記分試題的難度參數(shù)表示一道滿分為

m

的多級記分試題的難度參數(shù)(Embretson & Reise, 2000)。Logistic加權(quán)模型也以兩級記分Logistic模型為基礎(chǔ), 依據(jù)多級記分試題的分?jǐn)?shù)加權(quán)作用, 用

m

道難度相同的兩級記分試題的試題難度來描述一道滿分為

m

的多級記分試題的平均難度, 具體為：(1)用

m

道難度值相同的兩級記分試題的難度

b

表示為該道多級記分試題的平均難度, 即用一個難度參數(shù)

b

表示多級記分試題的平均難度; (2)用試題滿分

m

來表示試題的權(quán)重參數(shù), 以反映該試題考查知識的重要性程度。在Logistic加權(quán)模型下, 多級記分題的平均難度參數(shù)的參數(shù)含義與兩級記分試題的難度參數(shù)含義相似, 含義為：當(dāng)被試在某一多級記分題上的得分為中間得分及以下的期望概率累加和為0.5時, 此時該被試的能力估計值即是該多級記分題的平均難度參數(shù)。

2.2 Logistic加權(quán)模型的項目特征函數(shù)推導(dǎo)

在兩級記分試題時, 被試在中等難度試題上得分為1的作答情況為：在能力量尺低端, 低能力被試群體中答對此題的人數(shù)比例較小, 在能力量尺高端, 高能力被試群體中答對此題的人數(shù)比例大, 此時曲線呈單調(diào)上升趨勢, 其曲線描述為圖1中得分為1的曲線; 同時圖1也描述了得分為0時項目特征曲線：在能力量尺低端, 低能力被試群體中答錯此題的人數(shù)比例較大; 在能力量尺高端, 高能力被試群體中答錯此題的人數(shù)比例小, 此時曲線呈單調(diào)下降趨勢。由圖1也可描繪為

u

和

u

分以上的正確作答比例曲線圖, 為圖2。Baker和Kim (2004)描繪兩級記分試題項目特征曲線時也是用這兩種方式。

圖1 兩級記分題的項目特征曲線(恰得u分)

圖2 兩級記分題的項目特征曲線(得u分及以上)

圖3 多級記分題的項目特征曲線(恰得u分)

圖4 多級記分題項目特征曲線(得u分及以上)

Logistic加權(quán)模型表示

u

和

u

分以上的概率

3 模擬研究與實測數(shù)據(jù)分析

3.1 Logistic加權(quán)模型的參數(shù)估計

Logistic加權(quán)模型增加了權(quán)重參數(shù)即試題滿分值, 試題滿分值是在命題時確定, 有一定的主觀性,但測驗設(shè)計者需根據(jù)心理測驗設(shè)計藍(lán)圖(或教學(xué)大綱), 及測驗編制經(jīng)驗規(guī)律來確定試題滿分值, 因此試題滿分值可看成是人們對試題分?jǐn)?shù)權(quán)重共同認(rèn)識的間接反映, 可作為Logistic加權(quán)模型的權(quán)重參數(shù), 且不需要進(jìn)行估計。

Logistic加權(quán)模型可使用邊際極大似然估計EM算法(Bock & Aitkin, 1981)估算出兩級和多級記分試題的區(qū)分度、平均難度參數(shù)。根據(jù)全體被試的作答矩陣建立似然函數(shù)：

3.2 模擬研究與討論分析

以往兩級記分模型的模擬研究已經(jīng)論證了題量、被試量、試題難度分布會影響到測驗?zāi)M結(jié)果(吳佳儒, 陳柏熹, 2008; 朱隆尹, 丁樹良, 涂冬波,盧震輝, 2009)。這里探討Logistic加權(quán)模型下, 被試數(shù)量、試題滿分值這兩個因素對測驗?zāi)M返真性能的影響。

測驗?zāi)M設(shè)計為：被試數(shù)量分1000、5000; 試題滿分值分2, 3, 4, 5, 多個滿分值混合五種情況,測驗總分100分, 模擬重復(fù)50次。測驗?zāi)M所得的模擬返真性能結(jié)果如表1。

由表1, (1)被試數(shù)量對模擬結(jié)果的影響, 被試5000的各個測驗情境下ABS、RMSE, 比被試1000時的ABS、RMSE都要稍微小一些。在被試5000的各個情境下, Bias值都比較小, 表明偏差很小。相對于被試1000時, 被試5000時的各種題量下的Bias更接近0。(2)試題滿分值對模擬結(jié)果的影響。在被試5000或1000時, 當(dāng)滿分值從2到3, 4, 5分時, 試題區(qū)分度、難度的ABS、RMSE, 無明顯的變大或變小趨勢, 而且都在0.09以內(nèi)波動, 說明試題滿分值大小對測驗?zāi)M返真性能幾乎沒有影響。總之, 在各情境下Logistic加權(quán)模型的測驗?zāi)M返真性能良好。

表1 被試得分為連續(xù)時的模擬結(jié)果

本文還進(jìn)行了評分為非連續(xù)時的測驗?zāi)M, 發(fā)現(xiàn)模擬返真性能也相對良好。

將表1與以往兩級記分模型的模擬研究結(jié)果比較(朱瑋, 丁樹良, 陳小攀, 2006; 吳佳儒, 陳柏熹,2008), 發(fā)現(xiàn)本文的模擬返真性能結(jié)果與其他研究者的模擬返真性能結(jié)果很相近, 這也說明本文的測驗?zāi)M返真性能良好。

3.3 實測數(shù)據(jù)分析

4 結(jié)論

試題難度、試題考查重要性程度加權(quán)是多級記分試題的兩個基本屬性。依據(jù)多級記分試題在測驗設(shè)計時的分?jǐn)?shù)加權(quán)作用, 本文提出了Logistic加權(quán)模型并論述了其構(gòu)建思想, 同時推導(dǎo)了Logistic加權(quán)模型的項目參數(shù)估計EM算法并編寫了相應(yīng)的程序。在Logistic加權(quán)模型下進(jìn)行測驗?zāi)M并進(jìn)行項目參數(shù)估計, 發(fā)現(xiàn)項目參數(shù)估計的模擬返真性能良好。Logistic加權(quán)模型適合需要體現(xiàn)分?jǐn)?shù)權(quán)重作用的教育成就測驗、智力測驗等, 而使用多個分?jǐn)?shù)等級評定的人格測驗往往試題都是相同等級, 適合使用GRM。

Baker, F. B., & Kim, S. H. (2004).

Item response theory: Parameter estimation techniques

(2nd ed.). New York: Marcel Dekker, Inc.Bock, R. D., & Aitkin, M. (1981). Marginal maximum likelihood estimation of item parameters: An application of a EM algorithm.

Psychometrika, 46

, 443–459.Du, W. J. (2006). Information of IRT multilevel item.

Acta Psychologica Sinica, 38

(1), 135–144.[杜文久. (2006). 項目反應(yīng)理論框架下多級評分項目的信息函數(shù).

心理學(xué)報, 38

(1), 135–144.]Embretson, S. E., & Reise, S. P. (2000).

Item response theory for psychologists.

Mahwah, NJ: Lawrence Erlbaum Associates.Qi, S. Q., Dai, H. Q., & Ding, S. L. (2002).

Principles of modern educational and psychological measurement.

Beijing, China:Higher Education Press.[漆書青, 戴海崎, 丁樹良. (2002).

現(xiàn)代教育與心理測量學(xué)原理.

北京: 高等教育出版社]Samejima, F. (1969). Estimation of latent ability using a response pattern of graded scores.

Psychometrika Monograph Supplement, 34

(4), 100–114.van der Linden, W. J., & Hambleton, R. K. (Eds.). (1997).

Handbook of mo dern it em re sponse th eory

. New York:Springer.Wu, G. R., & Chen, B. X. (2008, November).

The influences of the sample sizes and ability distributions on the item and trait parameters measurement accuracy

. Paper presented at the meeting of the 8th cross–strait conference on psychological and educational testing, Kunming, Yunnan.[吳佳儒, 陳柏熹. (2008, 11).

受試者人數(shù)及能力分布型態(tài)對試題與能力參數(shù)估計的影響

. 第八屆海峽兩岸心理與教育測驗學(xué)術(shù)研討會, 云南, 昆明.]Xiao, H. M., Du, W. J., & Zhang, T. T. (2011). Deriving polytomous scoring models based on item node.

Acta Psy chologica Sinica, 43

(12), 1462–1467.[肖涵敏, 杜文久, 張婷婷. (2011). 基于項目節(jié)點的多級評分模型的統(tǒng)一.

心理學(xué)報, 43

(12), 1462–1467.]Zhu, L. Y., Ding, S. L., Tu, D. B., & Lu, Z. H. (2009). Comparison among parameter estimation methods based on small sample under item response theory.

Psychological Exploration,29

(5), 72–76.[朱隆尹, 丁樹良, 涂冬波, 盧震輝. (2009). 基于小樣本容量的IRT參數(shù)估計方法比較研究.

心理學(xué)探新, 29

(5),72–76.]Zhu, W., Ding, S. L., & Chen, X. P. (2006). Minimum chisquare/EM estimation under IRT.

Acta Psychologica Sinica,38

(3), 453–460.[朱瑋, 丁樹良, 陳小攀. (2006). IRT中最小化χ/EM參數(shù)估計方法.

心理學(xué)報, 38

(3), 453–460.]