兩種新的計算機化自適應測驗在線標定方法*
陳 平
(北京師范大學中國基礎教育質量監測協同創新中心, 北京 100875)
1 引言
在傳統紙筆測驗(Paper-and-Pencil, P&P)中,所有被試不論能力高低都作答相同的一批題目, 所以P&P中題目的難度分布較廣, 一般覆蓋整個能力范圍。于是, 題目對高能力被試而言大多比較容易、對低能力被試來說大多比較難, 不利于對被試能力的準確估計(漆書青, 戴海琦, 丁樹良, 2002)。計算機化自適應測驗(Computerized Adaptive Testing,CAT)的基本思路是讓計算機自動模仿聰明主試的做法, 每次都呈現最適合被試作答的題目(Wainer et al., 1990)。因此, 相對于P&P, CAT使用更少的題目就能達到相同的能力估計精度(如Weiss, 1982),大大提高了測驗效率。CAT還有很多其他優點, 比如:(1)隨著計算機硬件的不斷升級, 可以在短時間內完成越來越復雜的計算; (2)與多媒體技術結合可以提供包括音頻與視頻在內的新穎題目類型(如短時記憶題和空間記憶題)。如果有語音合成器, 還可進行聽力與口語測試; (3)與認知診斷相結合可以測量新的技能類型(如知識狀態); (4)與多級項目反應理論(Polytomous Item Response Theory, PIRT)結合可以提供基于表現的題目類型(如開放題); (5)與多維IRT (Multidimensional IRT, MIRT)相結合可以提供被試在多個分維度上的精細信息; (6)主試如果感興趣還可以記錄被試在每個題目上的反應時, 以作為評價被試能力的輔助指標(Wang, 2012); (7)當題庫得到良好維護時, 測驗可以全年提供, 被試可以選擇方便的時間參加測驗(Cheng, 2008)。上述優點使得國內外很多大規模的選拔性與資格性考試都推出CAT版本的測驗, 例如美國商學院研究生入學考試與美國醫生護士資格考試(Chang, 2012, 2015),還有我國第四軍醫大學對應征公民進行的圖形智力測驗(田健全, 苗丹民, 楊業兵, 何寧, 肖瑋, 2009)等。
題庫是CAT的重要組成部分, 也是CAT順利實施的重要前提。構建CAT題庫一般包括“明確題庫大小”、“確定題庫結構”、“開發題目”以及“標定題目參數”等核心步驟(陳平, 2011; Flaugher, 2000),每個步驟的完成質量都會影響題庫質量, 進而影響在后續評分過程中對被試能力進行估計的準確性。而且CAT在使用一段時間后, 對題庫的維護與管理就顯得尤為重要, 因為題庫中的某些題目會因為過度曝光、過時等原因不再適合被繼續使用(Wainer& Mislevy, 1990)。對此, 游曉鋒、丁樹良和劉紅云(2010)建議暫時“休眠”過度曝光的題目, 同時淘汰過時的題目; Guo和Wang (2003)建議不斷開發新題對存在問題的題目進行替代, 并標定其參數, 然后將其增補到題庫當中。在整個題目增補過程中, 對新題的標定是技術難點, 題庫管理者需要盡可能準確地標定新題, 因為標定不準的題目會產生有偏的能力估計值(陳平, 辛濤, 2011a, 2011b)。為了實現這個目標, 在線標定技術被廣泛應用于CAT的新題標定中(如Chang & Lu, 2010), 主要是因為它相對于傳統的錨題設計的離線標定方法具有諸多優點(詳見Chen, Xin, Wang, & Chang, 2012; Parshall, 1998)。
在線標定是指在被試自適應作答舊題的過程中將新題以隨機或自適應的方式分配給被試作答,并在線收集被試在新題上的作答反應, 然后估計新題參數的過程(Wainer & Mislevy, 1990)。經過在線標定后的新題參數自然而然地與舊題參數在同一量尺上, 不再需要進行等值(Ban, Hanson, Wang, Yi, &Harris, 2001; 陳平, 辛濤, 張佳慧, 2013)。考慮到CAT本身的性質以及實際中每名被試作答的新題數一般少于新題總數(Ban, Hanson, Yi, & Harris, 2002),被試在舊題和新題上的作答反應均構成稀疏矩陣而非全矩陣, 因此IRT中傳統的適用于全矩陣情形的題目參數估計方法就不能直接應用于在線標定情境, 而需要進行相應的調整。為了解決在線標定中的數據稀疏問題, 研究者在過去30年里提出多種在線標定方法/設計, 比如Stocking (1988)的Method A和Method B, Wainer和Mislevy (1990)的“只有一個EM循環”方法(OEM), Ban等人(2001)的“有多個EM循環”方法(MEM)以及BILOG/Prior方法。Ban等人(2001)在3種樣本量(300、1000和3000)下對上述5種方法的題目參數返真性進行比較, 結果表明:(1) Method A由于存在理論缺陷(即將能力估計值視為能力真值), 具有最大的標定誤差; (2) MEM在所有樣本下都有最小的標定誤差, 因此表現最優;(3) MEM的表現優于OEM, 但是當部分新題質量較差時, OEM的表現也有可能優于MEM。其他的方法/設計還包括游曉鋒等人(2010)的雙參數條件極大似然估計(Conditional Maximum Likelihood Estimation, CMLE)與多重迭代CMLE方法(這兩種方法類似于Method A)、Chang和Lu (2010)的序貫設計以及van der Linden和Ren (2015)的最優貝葉斯自適應設計等。
在已有的在線標定方法中, Method A無論是在思路層面還是在具體實施層面都是最簡單、最直接的方法, 它可簡述為3個步驟:(1)基于被試在舊題上的作答采用CMLE估計被試能力; (2)將被試能力估計值視為能力真值; (3)基于被試在新題上的作答并結合能力“真值”再次使用CMLE估計新題參數。注意第2步的關鍵假設使得Method A在標定新題的過程中忽略了能力的估計誤差。可以預見的是,當能力估計誤差較大時, Method A的表現勢必會受到較大影響。為了克服Method A的理論缺陷, 本文提出兩種新的CAT在線標定方法:第一種方法將全功能極大似然估計量(Full Functional MLE, FFMLE)(Jones & Jin, 1994; Stefanski & Carroll, 1985)與Method A相結合(記為FFMLE-Method A), 具體是采用FFMLE能力估計量代替Method A中的CMLE能力估計量以校正能力的估計誤差; 第二種方法將Stefanski和Carroll (1985)提出的另一個估計量——“利用充分性結果”的估計量(an Estimator which Exploits the Consequences of Sufficiency, 簡記為ECSE)與Method A相結合(記為ECSE-Method A),并用于替換Method A中的CMLE能力估計量。本文采用蒙特卡洛模擬方法在多種測驗情境下將兩種新方法與Method A進行全面比較, 并將Ban等人(2001)認為表現最好的MEM作為標桿進行參照。
本文的剩余部分按如下方式進行組織:下一節將詳細描述方法部分(包括IRT模型、FFMLE方法、ECSE方法以及新提出的FFMLE-Method A和ECSE-Method A)。接下來在第3節詳細介紹模擬研究設計, 并在第4節呈現研究結果與結論。最后一節呈現討論部分以及今后的研究方向。
2 方法
2.1 IRT模型
由于本文提出的兩種新方法是基于FFMLE和ECSE而構建, 而FFMLE和ECSE是基于標準形式的邏輯斯蒂克回歸(Logistic Regression, LR)框架而開發, 又因為兩參數邏輯斯蒂克模型(Two- Parameter Logistic Model, 2PLM) (Birnbaum, 1968)可視為包含潛變量θ的標準形式LR模型, 所以本文選擇2PLM作為IRT模型1這里暫未考慮3PLM的原因是:3PLM的項目特征函數 (ICF) 是在2PLM的ICF的基礎上乘以 (1-c) 再加上c而得到 (c代表猜測參數)。對于這種在標準形式LR模型的基礎上進行簡單變換而得到的模型, FFMLE與ECSE是否仍具有優良的統計特性還有待進一步的考證。。2PLM的項目特征函數為
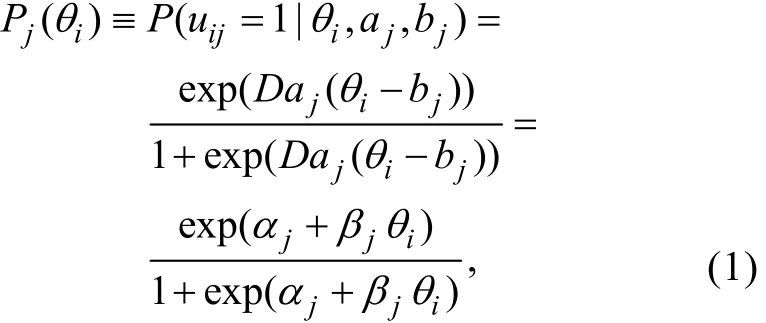
其中uij表示被試i在題目j上的作答,θi表示被試i的能力參數,aj和bj分別是題目j的區分度與難度參數;是以LR模型的標準形式表達的題目參數向量, 其中αj=?Daj bj、βj=Daj;Pj(θi)表示能力為θi的被試i正確作答題目j的概率。上式中的D是量表因子,D=1表示使用邏輯斯蒂克量尺,D=1.702表示使用正態量尺。本文取D=1.702。
2.2 FFMLE與ECSE方法
步驟1:定義測量誤差模型

其中εi是對θi進行觀測時得到的誤差項。給定θi的情況下, 模型假設εi服從均值為0、方差為σ2的正態分布(εi~N(0,σ2))且εi與uij相互獨立(Cov(εi,uij)=0), 于是有, 而且的概率密度函數可表示為
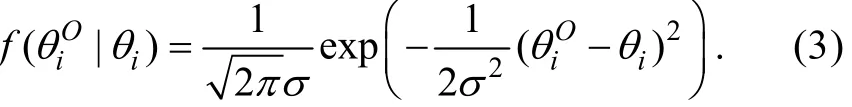
上述測量誤差模型中的誤差方差σ2不含下標i, 說明該模型假設不同觀測的測量誤差具有相同的方差。
步驟2:構建未知參數和Δj的全功能對數似然函數l( θ, Δj)
Carroll, Ruppert, Stefanski和Crainiceanu (2006)提到在經典的功能模型中,θi(i=1,2,...,N)可視為未知參數, 而且通過最大化觀測數據的聯合密度可以得到和Δj的FFMLE估計量。另外, 由步驟1的假設可知,εi與uij相互獨立, 進而得到也相互獨立。因此,在給定參數特定取值θi和Δj的條件下,的聯合密度為
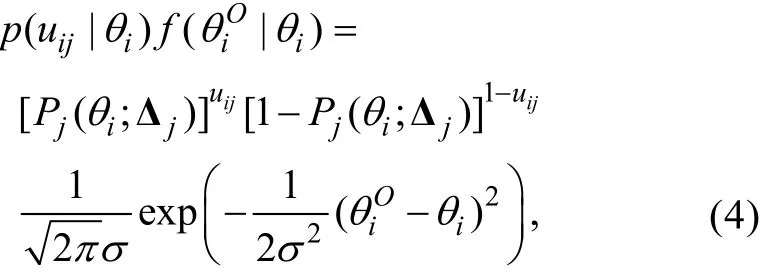
其中Pj(θi;Δj)即公式(1)中的Pj(θi), 表示其是θi和Δj的函數。于是l( θ, Δj)可表示為
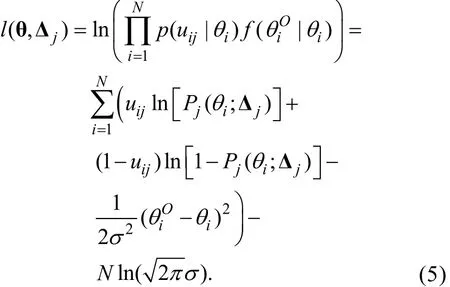
步驟3:將l( θ, Δj)分別對和Δj求偏導后令它們等于0, 可知θi和Δj的MLE估計值滿足以下等式組
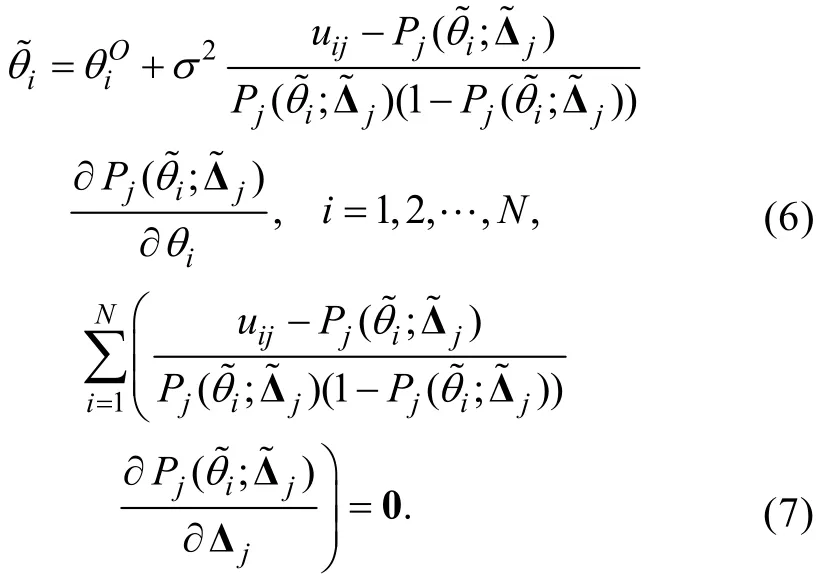
考慮到(6)式中的誤差方差2σ未知而且從(6)式和(7)式中求解非常困難, Stefanski和Carroll(1985)建議對(6)式進行如下修改, 以獲得的近似版本。
步驟4:將(6)式等號左邊的替換為

對比(8)式和(6)式容易發現, 步驟4實際上是分別使用對(6)式等號右邊的進行替換, 其中是估計的誤差方差, 可以使用MLE的漸近方差公式對其進行估計(Lord, 1980);進行傳統LR后得到的MLE估計值;是校正后的估計量, 它從理論上校正蘊含在中的測量誤差。對于2PLM,, 于是(8)式可簡化為

步驟5:將uij對校正后的進行傳統LR后得到的MLE估計量, 即是Δj的FFMLE估計量。
另外, Stefanski和Carroll (1985)在誤差正態的假設下還發現:在給定Δj和σ2時, 可以找到θi的充分統計量——, 即uij的條件分布在給定T(Δj)時不依賴于θi。相應地,他們根據充分性的結果給出另一種校正測量誤差的方法——ECSE。ECSE與FFMLE的不同之處僅體現在步驟4, ECSE使用下式對測量誤差進行校正
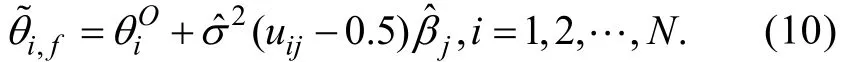
Stefanski和Carroll (1985)的研究表明:當觀測數N足夠大且無限趨近于σ2時(即當N→∞時,), FFMLE和ECSE估計量都具有一致性而且表現都優于傳統的MLE估計量。
2.3 FFMLE-Method A與ECSE-Method A方法
鑒于Method A存在的天然理論缺陷以及FFMLE和ECSE具有的優良性質, 本節將FFMLE和ECSE的誤差校正思路融入Method A并得到兩種新方法FFMLE-Method A和ECSE-Method A。
在一般正則條件下, 當測驗長度t→∞時, CAT的MLE能力估計值漸近服從正態分布是對能力真值θ進行估計i的誤差方差,I(θi)是θi處的費舍測驗信息量,與θi的接近程度由I(θi)或φi的大小決定(Chang &Stout, 1993)。值得注意的是, 在CAT測驗情境中,不同被試可能會得到不同的誤差方差φi(與下標i有關), 這與FFMLE和ECSE中測量誤差模型的假設稍有不同。但是, 如果將2.2節步驟1中的測量誤差模型修改為, 關于FFMLE和ECSE的主要結論會保持不變。相應地,當t→∞時, 能力估計誤差也漸近服從正態分布N(0,φi)。由于ξi具有漸近正態性, 滿足FFMLE和ECSE的前提假設, 所以在CAT新題標定過程中也可以借鑒FFMLE和ECSE的思路對ξi進行校正, 然后再基于校正后的能力估計量采用Method A標定新題。對于新題j, FFMLE-Method A和ECSE-Method A可描述為以下6個步驟(兩者的差異僅體現在步驟5):
步驟1:CAT結束后, 采用CMLE可以得到作答新題j的所有被試的能力估計值及相對應的能力估計誤差方差。即可得到,其中nj表示作答新題j的被試數,分別表示作答新題j的第i名被試的能力估計值及估計誤差方差。對于2PLM,可通過下式計算
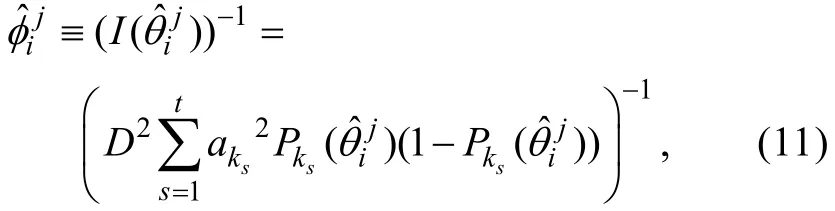
其中k為作答新題j的第i名被試的被試編號,表示被試k作答的t個舊題的題目編號。在CAT過程中, 還可收集被試在所有新題上的作答, 其中T表示轉置運算,m表示新題總數。另外, 當t→∞時,, 其中都表示參數真值而且。
步驟2:將上一步得到的視為能力真值, 結合xj采用Method A估計新題j的題目參數向量, 得到(為步驟5做準備)。
步驟3:構建未知參數和γ的
j全功能對數似然函數
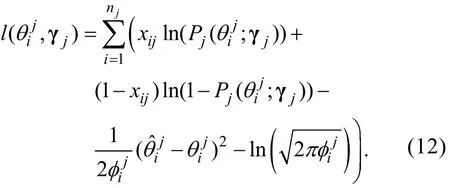
步驟4:將分別對和γj求偏導, 并令它們等于0, 可得知的MLE估計值滿足以下等式組
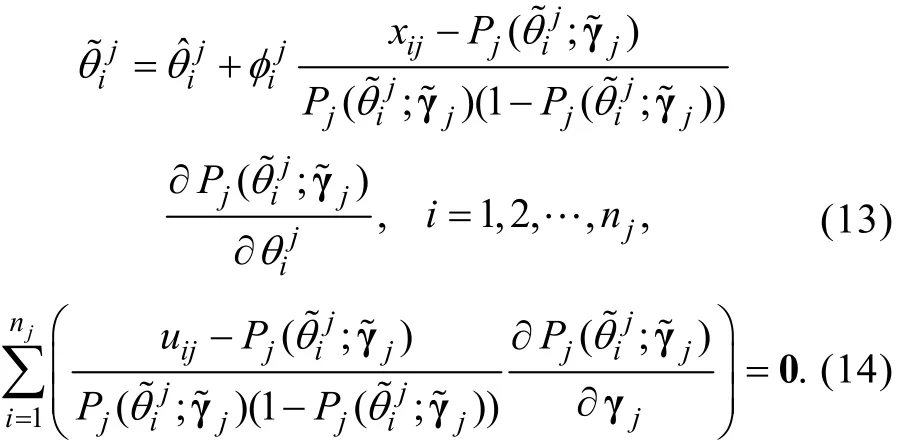
步驟5:對(13)式進行修改如下
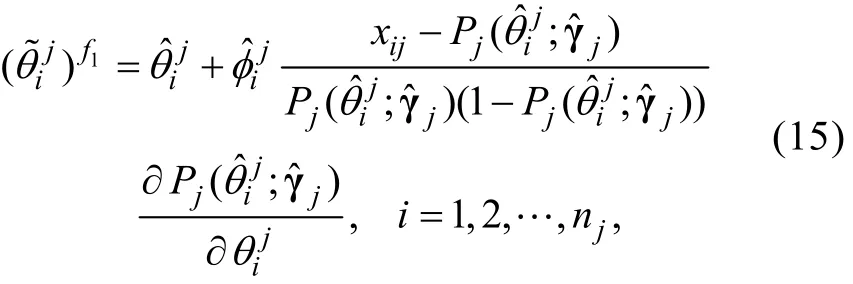
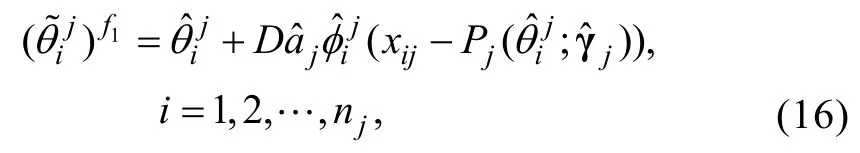
類似于公式(10), 這里的ξi也滿足漸近正態性,也可采用ECSE方法對能力估計誤差進行校正
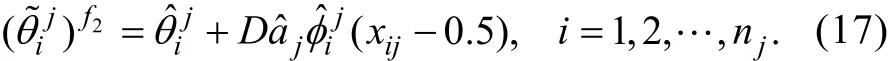
步驟6:基于上一步得到的以及xj, 再次采用Method A估計γj,得到的估計量即是FFMLE-Method A或ECSE-Method A估計量。
對每個新題都執行上述6個步驟后即可實現對所有新題的標定。一方面估計了所有新題的題目參數,另一方面將所有新題參數都置于舊題的參數量尺上。
3 實驗
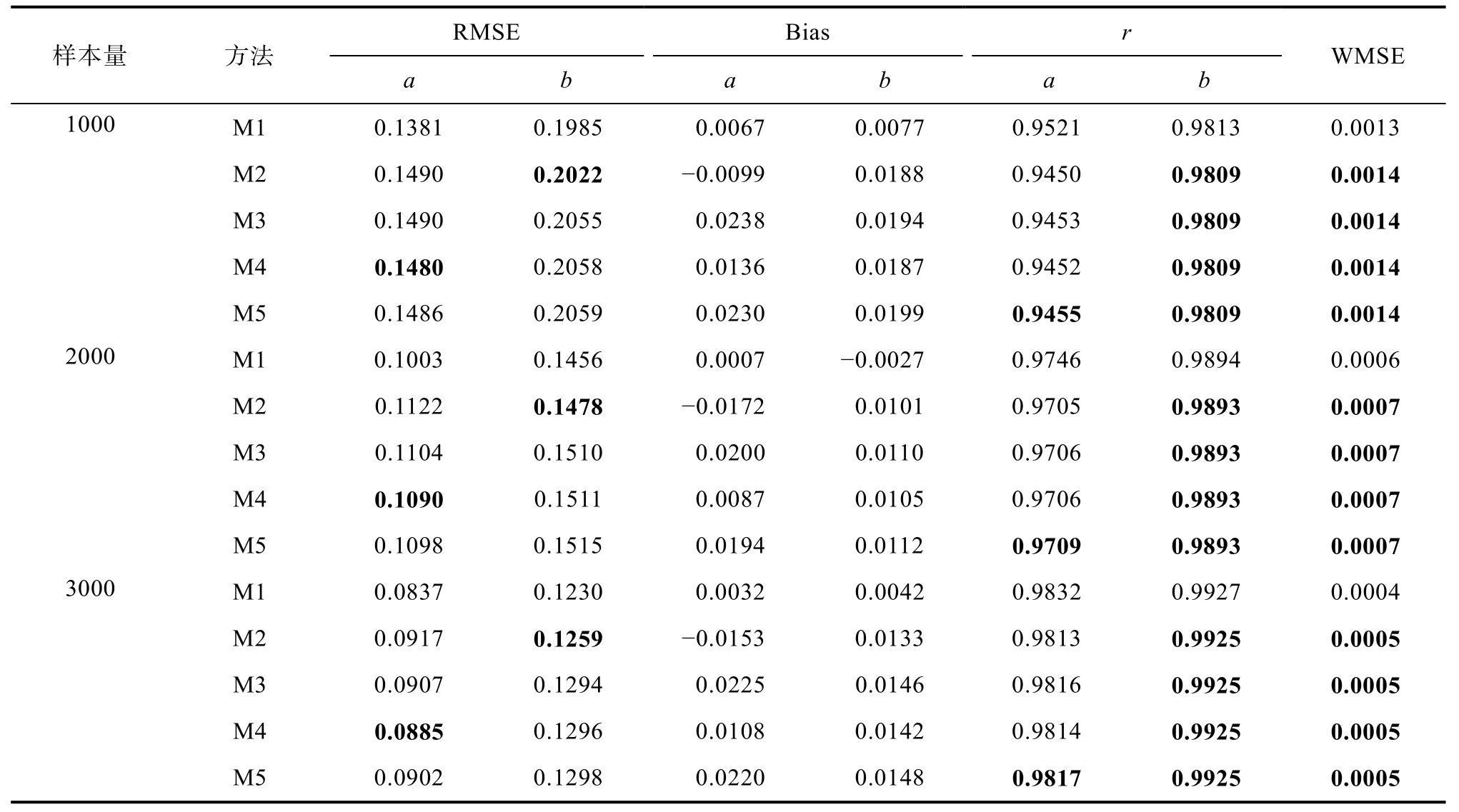
本研究的主要目的是在多種測驗情境下考察新提出的FFMLE-Method A和ECSE-Method A較原始的Method A [記為Method A (Original)]和MEM能否改進標定精度。另外, 考慮到Method A的表現在很大程度上依賴于能力估計值與能力真值的距離遠近, 因此本文還想知道:如果被試的能力真值已知, Method A的標定精度能夠得到多大程度的提高。這在模擬研究中可以實現, 即在Method A中使用真實的能力值, 這種方法可作為比較的基準[記為Method A (True)]。所以, 本研究采用模擬方法對Method A (True)、Method A (Original)、FFMLEMethod A、ECSE-Method A以及MEM等5種CAT在線標定方法進行全面比較。
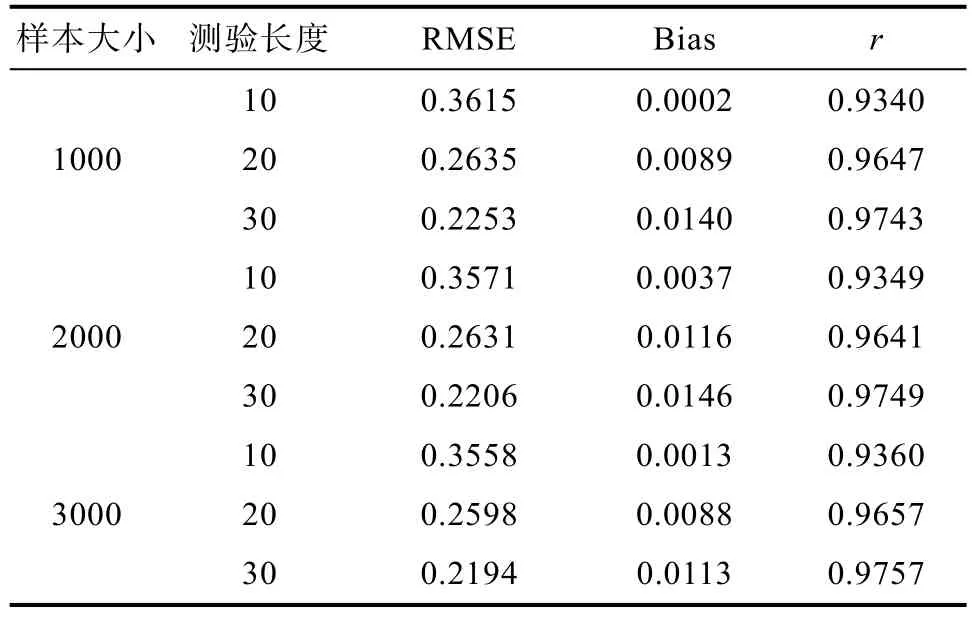
為了探討樣本大小對標定精度的影響, 本研究考慮3種樣本大小(N=1000,2000和3000)。考慮到CAT測驗長度會影響能力的估計精度, 本研究還采用3種測驗長度(t=10,20和30), 旨在討論不同測驗長度對標定精度的影響。因此, 本研究采用3× 3× 5的實驗設計, 共產生45種實驗條件、9種CAT測驗情境(即在樣本大小與測驗長度組合的每種CAT測驗情境下, 都采用5種方法標定新題)。本文采用Matlab R2013a編寫計算機模擬程序, 并將9個模擬程序(1種測驗情境對應1個程序)部署在9臺虛擬機上分別運行, 以節省程序運行時間。另外, 盡管本文不比較不同樣本量或不同測驗長度對在線標定方法運行時間的影響, 但還是將9臺虛擬機設為相同配置, 即64位的操作系統、2.60 GHz的處理器(雙核)以及8GB的內存2值得注意的是, 實驗表明:即使在配置完全相同的多臺虛擬機上運行同一個程序, 也不會得到完全相同的運行時間結果。所以從嚴格意義上講, 本文不能準確考查不同樣本量或不同測驗長度對在線標定方法運行時間的影響, 但可比較同一CAT測驗情境內不同方法的運行時間。。
3.1 被試與題庫生成
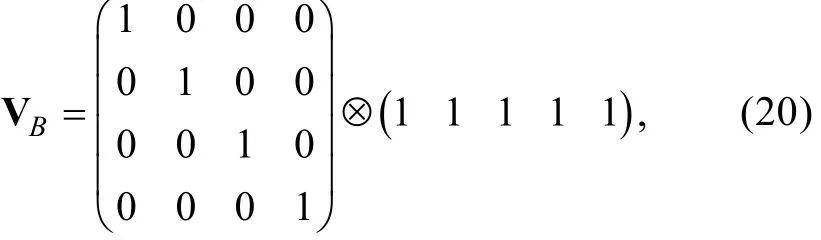
本研究模擬3個被試樣本(對應于3種樣本大小), 每個被試樣本的能力真值都隨機抽取自標準正態分布。對于所有9種測驗情境, 模擬1000個題目構成CAT題庫, 題庫中題目的參數向量γ=(a,b)T隨機抽取自均值向量為μγ、協方差矩陣為Σγ的多變量正態分布MVN( μγ,Σγ), 其中。為了使得生成的題目參數盡可能與真實情境相符, 借鑒Chen和Xin (2014)的方法確定μγ和Σγ中的參數:(1)假設b隨機抽取自標準正態分布, 于是μb=0、var(b)=1; (2)一般情況下a和b存在一定程度的正相關(Chang, Qian, & Ying, 2001), 這里假設a和b間的相關系數ρa,b=0.25; (3) Baker和Kim (2004)認為a一般服從對數標準正態分布(lna~N(u,σ2),其中u=0、σ=1)并且a的取值一般落在某個范圍(如a∈(LBa,UBa))。于是想知道, 在a取值范圍被截取的情況下,a的均值μa和方差var(a)會是多少。根據Lien (1985)的研究結果, 可知截取的對數正態分布的r次矩可描述為

表1 模擬的被試樣本與題庫的描述統計量

其中E(ar)=exp(ru+(r2σ2/2)), Φ(?)是標準正態分布的累積分布函數。這里假設LBa=0.2、UBa=2.0,容易得到E(a|0.2 另外, 將模擬生成的θ和b截取在?3至3之間,a介于0.2至2.0之間。模擬的3個被試樣本以及題庫的描述統計量如表1所示。模擬生成的a與b之間的相關系數等于0.2507, 與預設的真值0.25非常接近。 對每種測驗情境, 都模擬生成20個新題(m=20)。為了減少隨機誤差, 對包括生成新題、模擬被試在新題上的作答以及標定新題的整個過程重復100次(rep=100)。另外, 模擬新題參數的方法與模擬舊題參數的方法相同, 也是從(19)式所示的先驗分布中隨機抽取。同樣, 新題的a介于0.2至2.0之間,b介于?3至3之間。 從初始題的選擇方法、選題策略、能力估計方法以及終止規則等方面對CAT全過程的模擬進行描述:(1)一開始對被試能力一無所知, 所以將每名被試的能力值初始化為0 (即=0); (2)基于被試的能力估計值, 采用最大費舍信息量方法從題庫或剩余題庫中選擇第一個或下一個最適合被試作答的題目施測被試; (3)根據當前被試的能力真值以及當前題目的參數真值基于2PLM計算正確作答概率P, 然后將P與從均勻分布U(0,1)中隨機抽取的小數z進行比較。如果P≥z, 模擬作答為1; 否則, 模擬作答為0; (4)被試完成對每個題目的作答后, 對被試能力的更新分為兩種情況:當測驗長度較短(比如小于5)或出現全0或全1的作答模式時, 采用后驗期望法(Expected A Posteriori, EAP)更新被試的能力估計值; 否則, 采用MLE方法對進行更新; (5)采用固定長度的終止規則, 并且預設測驗長度分別為t=10,20和30。也即上述的題目選擇、作答模擬以及能力估計等過程不斷重復, 直至測驗長度達到t為止, 結束測驗。 在模擬CAT時還有一些重要細節值得強調:(1)在實現EAP時, 假設能力的先驗分布為標準正態分布, 并且在[?3, 3] 上均勻抽取61個積分結點3選取61個積分結點的理由是:在預研究中, 我們考查了3種不同積分結點數 (分別為21個、41個和61個) 對EAP估計精度的影響。結果發現, 使用21個積分結點的精度最差, 采用41個結點已經可以得到較高的估計精度, 但為了保險起見, 還是選取61個結點。(S=61), 于是步長step=6(S?1)=0.1, 積分結點qs=(?3)+(s?1)×step以及與之相伴隨的權重; (2)在實現MLE時, 采用牛頓?拉夫遜方法(Newton-Raphson, N-R)與二分法相結合的方式求解非線性方程。而且在具體編程時, 一般先采用速度較慢的二分法尋找包括零點的區間, 待找到后再換用迭代速度較快的N-R (迭代精度設為0.001); (3)不管是采用EAP還是MLE, 都將最終的能力估計值截取在[?3, 3] 之間。也即, 當能力估計值大于3時, 將其賦值為3; 當能力估計值小于?3時, 將其賦值為?3。 由于在線標定包括在線標定設計與在線標定方法兩個重要環節(陳平等, 2013), 所以接下來分別對兩者的實施細節進行描述。 考慮到隨機在線標定設計實施起來非常方便而且能夠提供準確穩定的標定結果(比如Ban et al.,2001; Chen et al., 2012), 本研究在CAT測驗過程中采用隨機在線標定設計將新題分配給被試作答。具體而言, 首先從由20個新題組成的新題集中隨機選擇5個新題(即C=5), 然后將它們置于被試CAT的隨機位置。另外, 由于參與作答每個新題的被試數會影響新題的標定精度, 因此參照Chen等人(2012)的做法, 本研究也將作答每個新題的被試數都控制在平均水平——(N×C)m, 也即對于3種樣本大小, 作答每個新題的被試數分別控制在250((1000× 5)20)、500((2000× 5)20)和750((3000× 5)/20)。這可以通過預先構建一個行和都等于C、列和都等于(N×C)m的隨機矩陣V=(vij)N×m來實現,其中vij用于標識被試i是否會作答新題j。vij=1表示被試i會作答新題j, 否則vij=0。以3000的樣本大小為例, 簡單說明V的構建方法:首先構建大小為(m C)×m(即4× 20)的基本矩陣單元VB 其中?表示克羅內克積(kronecker product)符號,易知VB的行和都等于C(即5)、列和都等于1。所以, 如果將(N×C)m(即750)個VB縱向合并(或將?右邊的行向量換成大小為750× 5且元素全由1組成的矩陣)然后隨機調換行的位置、列的位置, 即可得到行和都等于C、列和都等于(N×C)m的矩陣V。對于1000和2000的樣本大小, V的構建方法類似。 CAT測驗結束后, 計算機已經收集所有被試在舊題上的作答以及在新題上的作答,根據與已知的舊題參數還可計算所有被試的能力估計值以及相對應的能力估計誤差方差。接下來, 再使用本文討論的5種方法對新題進行標定。注意在具體實施不同方法時, 可能會用到上述的不同信息。比如, 對于Method A (True), 只需要被試能力真值就能標定新題; 而對于Method A (Original), 需要用于新題標定; 對于FFMLE- Method A和ECSE-Method A, 則需要用到以及Method A (Original)得到的估計結果等信息; 實施MEM需要用到以及等信息。 本文討論的5種方法在算法層面都需要使用N-R迭代, 而且預研究(未考慮新題參數的先驗分布)還發現:當用于標定新題的被試數較少(比如本文1000的樣本大小所對應的250)時, 容易出現迭代不收斂的情況。為了解決此問題, 本研究將貝葉斯眾數估計(Bayes Modal Estimation) (Mislevy,1986) 的思路融入到這5種方法中, 即使用貝葉斯版本的在線標定方法, 也即在標定過程中考慮新題參數的貝葉斯先驗。雖然以往有些研究(比如Ban et al.,2001)使用固定的貝葉斯先驗, 但在在線標定情境下, Wainer和Mislevy (1990)提出更為合理的方案:首先對題庫中所有舊題的參數分布進行分析, 然后將其作為新題參數的先驗分布。基于此, 本文將(19)式所示的舊題參數先驗分布作為新題參數的先驗分布, 記為g(γ)。值得注意的是, 貝葉斯版本的在線標定方法較原始版本方法的變化僅在于:在對數似然函數項(對于前4種方法)或對數邊際似然函數項(對于MEM)后面都增加了貝葉斯先驗項——lng(γ)(詳見Baker & Kim, 2004; Zheng, 2014)。 其中函數norminv(?)用于計算標準正態累積分布函數的逆,prj表示作答新題j的所有被試在該題上的通過率,aμ是舊題a參數的先驗均值。 對于每種測驗情境, 采用均方根誤差(Root Mean Squared Error, RMSE)、偏差(Bias)以及皮爾遜相關系數(r)評價CAT的能力估計精度, 使用RMSE、Bias、r以及加權均方誤差(Weighted MSE,WMSE)評價各種方法的標定精度。采用最小EM循環數(Min_Cycle)、最大EM循環數(Max_Cycle)、平均EM循環數(Mean_Cycle)評價MEM的標定效率, 使用平均程序運行時間(Mean_Time)評價各種方法的標定時間。 Bias指標中各符號的含義同RMSE指標, 兩者都是越小越好。 該指標用于評價題目參數的總體返真性, 具體計算估計的項目特征曲線(Item Characteristic Curves, ICCs)與真實ICCs的平均加權面積差異。 因為MEM一般需要多次EM循環才能滿足收斂標準, 所以記錄這些指標以評價MEM的標定效率。 其中EM_Cycle(c)是第c次重復時MEM所需的EM循環次數, 函數min(?)、max(?)和round(?)分別用于求取最小值、最大值和四舍五入值。這3個值都是越小越好, 說明效率越高。 該指標用于反映采用每種方法標定所有新題的平均計算時間, 單位是秒。 其中Running_Time(c)表示第c次重復時運行某種在線標定方法程序所用的時間。值越小說明標定效率越高。 另外, 本研究還使用r衡量能力(題目)參數估計值與真值間線性關系的程度大小,r值越高說明能力估計精度或題目標定精度越高。 本文從三個方面對研究結果(如表2至表7所示)進行分析:(1)不同測驗情境下CAT的能力估計精度; (2)不同測驗情境下各種方法的標定精度; (3)不同測驗情境下各種方法的標定效率。 表2描述的是在9種測驗情境下模擬的CAT測驗的能力估計精度。由表中數據可知, 所有測驗情境下得到的Bias都非常接近0, 范圍從0.0002到0.0146。而且不管樣本量有多大, RMSE都隨測驗長度的增加而嚴格單調遞減,r都隨測驗長度的增加而嚴格單調遞增。比如, 對于1000的樣本大小, 當測驗長度從10增加到30時, RMSE分別為0.3615、0.2635和0.2253; 對于3000的樣本大小, 當測驗長度從10增加到30時,r從0.9360增加到0.9757。總體來講, 模擬的CAT能夠為被試提供準確的能力估計值。 表3至表5呈現的分別是測驗長度為10、20和30時不同樣本量下各種方法的標定精度結果。為了描述方便, 分別將Method A (True)、Method A(Original)、FFMLE-Method A、ECSE-Method A以及MEM記為M1至M5。值得強調的是, 對于樣本量N=1000、2000和3000, 分別有250、500和750名被試參與每個新題的標定。而且在所有測驗情境下的所有100次重復中, 5種方法的迭代程序都正常收斂, 這說明使用貝葉斯版本的在線標定方法可以避免N-R迭代不收斂的問題。 表2 不同測驗情境下CAT的能力估計結果 由表3可以看出, 3種樣本量下的Bias都非常接近0, 范圍從?0.0985到0.0072, 這說明估計的題目參數與真實題目參數間的平均差異較小, 對題目參數的修復能力較強。另外, 將兩種新方法M3和M4與M2進行比較, 可以發現:(1)從題目參數的總體返真性來看, M3和M4的WMSE與M5的值相同, 而且都一致小于M2的WMSE, 這說明對能力估計誤差進行校正可以改進Method A的標定精度,符合預期假設; (2)當樣本量為1000時(nj=250),M3和M4在a上的RMSE (分別為0.1616和0.1678)明顯小于M2的值(0.1943), 但在b上的標定精度有微小的降低(相對于M2, M3和M4在a上的RMSE降低16.83%和13.64%、而在b上的RMSE僅增加1.02%和1.36%)。但是當樣本量增加到2000和3000時(nj=500和750), M3和M4較M2的優勢開始突顯, M3和M4在a和b上的RMSE都明顯小于M2的相應值。這說明當樣本量足夠大時, FFMLE和ECSE的優良性質得到充分體現, 這與 Stefanski和Carroll (1985)的研究結果一致; (3)盡管M3與M4的表現比較接近, 但還是可以看出M3總體上優于M4, 這說明使用(16)式對能力估計誤差進行校正比使用(17)式進行校正能夠獲得更準確的標定結果。而且M3的表現已經非常接近于性能最優的M5; (4)樣本量越大, RMSE和WMSE都越小、r越大, 說明標定精度越高。 當測驗長度由10增加到20時, CAT提供的能力估計精度已有較大幅度的提高(詳見表2), 留給M3和M4“通過校正能力估計誤差改進標定精度”的空間就更小了。于是可以預見M3和M4較M2的改進幅度相對于測驗長度為10時會更小一些,這通過觀察表4中數據可以得到證實, 具體體現在:(1) M2、M3、M4與M5的WMSE已基本相同(特例是:當樣本量為2000時, M2的WMSE稍高一點); (2)在所有3種樣本量下, M3和M4在a上的RMSE都比M2的稍低一些, 然而它們在b上的RMSE都要比M2的稍高一些。至于為什么這兩種新方法不能像游曉鋒等人(2010)的方法一樣可同時改進a和b的估計精度, 原因可能是:a本質上是2PLM中θ的回歸系數, 非常容易受到θ的測量誤差的影響; M3與M4對中蘊含的測量誤差進行校正, 從而可提高a的標定精度, 但是并未采取類似于“夾逼平均法” (游曉鋒等, 2010)的任何措施以提高b的標定精度。總體而言, M3和M4的表現還是優于M24當樣本量為1000時, 相對于M2, M3和M4在a上的RMSE降低4.04%和4.11%、而在b上的RMSE只增加0.78%和0.82%; 當樣本量為2000時, 相對于M2, M3和M4在a上的RMSE降低9.59%和9.34%、而在b上的RMSE只增加1.88%和1.94%; 當樣本量為3000時, 相對于M2, M3和M4在a上的RMSE降低11.84%和11.93%、而在b上的RMSE只增加3.05%和3.37%。所以, 如果將a和b的標定精度看成同等重要的話, M3和M4的表現在總體上優于M2。; (3) M4的表現與M3和M5的表現已非常接近。一種可能的解釋是:M4受測驗長度的正面影響(即測驗長度越長, M4的相對表現更好)可能較M3更大一些; (4)隨著樣本量的增大, 標定精度也提高。另外, 3種樣本量下的Bias也都非常接近0,范圍是從?0.0421到0.0161。 表3 測驗長度為10時不同樣本量下各種方法的標定結果 表4 測驗長度為20時不同樣本量下各種方法的標定結果 隨著測驗長度增加到30, CAT的能力估計精度進一步提高, 留給M3和M4的改進空間進一步減小, 主要表現在以下方面:(1) M2、M3、M4與M5在3種樣本量下的WMSE完全相等; (2)當用于標定新題的被試數較少時(nj=250), 相對于M2, M3沒有改進標定精度。只有當nj達到500甚至是750時,M3通過校正能力估計誤差在a上可以小幅度改進M2的標定精度; (3)注意當測驗長度達到30且樣本量為2000和3000時, M4已經成為總體上表現最好的方法5當樣本量為2000時, 相對于M2, M4在a上的RMSE降低2.85%、而在b上的RMSE增加2.23%; 當樣本量為3000時, 相對于M2, M4在a上的RMSE降低3.49%、而在b上的RMSE增加2.94%。同樣,如果將a和b的標定精度看成同等重要的話, M4的表現在總體上優于M2。, 這進一步證實M4受測驗長度的正面影響較大。另外, 樣本量越大, 標定精度也越高。而且3種樣本量下的Bias也都非常接近0, 范圍從?0.0153到0.0238。 表6描述的是9種測驗情境下關于MEM方法EM循環次數的統計結果。從表中可以看出, 在所有測驗情境下, MEM的標定效率都比較高, 最多只需要7次EM迭代就能滿足收斂標準, 最少只需要3次迭代就能收斂, 平均迭代次數為6次(當測驗長度為10時)或4次(當測驗長度為20和30時)。而且還可以發現:MEM所需的EM迭代次數受樣本量影響不大, 但會受測驗長度的影響, 比如當測驗長度增加時, 最大迭代次數單調遞減(注意有一個特例, 即當測驗長度為30且樣本量為2000時, 最大迭代次數是5)。這主要是因為如果被試作答更多的舊題, 在MEM的E步中就可以得到更精確的能力后驗分布, 從而導致更快的收斂。 表5 測驗長度為30時不同樣本量下各種方法的標定結果 表6 不同測驗情境下MEM的EM循環次數結果 表7呈現的是在9種測驗情境下各種方法的平均運行時間。從表中容易看出, 在所有測驗情境下,Method A類4種方法(M1、M2、M3和M4)的標定效率都很高, 整個標定過程在瞬間完成, 平均用時不到0.02秒。而且還可以發現:相對于M1和M2,M3和M4所花的時間稍多一點, 這主要是因為M3和M4首先在M2的基礎上對能力?θ中包含的測量誤差進行校正, 然后再基于M2標定新題。相比之下, MEM的算法更復雜, 所需的平均運行時間明顯更多(范圍在6.0827秒與21.0330秒之間), 所花時間約為其他4種方法的544倍至1618倍之間。盡管如此, MEM這種運行時間上的增加并不具有顯著的實際意義, 因為即使采用算法最復雜的MEM也只需22秒不到的時間即可完成標定任務。但是當將這些方法推廣到多維CAT情境時, Method A類4種方法較MEM的時間優勢就開始突顯。在一項預研究中發現:Method A類4種方法的多維版本只需2秒以內的時間即可完成標定, 而MEM的多維版本則需要長達1至2個小時的運行時間, 這在實踐中可能難以接受。 表7 不同測驗情境下各種方法的平均運行時間 基于上述研究結果, 可以得出以下結論: (1)當CAT測驗長度較短或中等時(比如t=10或t=20), MEM總體上表現最優。新方法FFMLE-Method A和ECSE-Method A較Method A總體上可以改進標定精度(t=10時的改進幅度最大), 而且與MEM的表現非常接近6其實在標定新題的過程中, MEM也和兩種新方法一樣對能力估計誤差進行了控制。具體表現在:MEM在M步中是通過最大化對數邊際似然函數來估計新題參數, 而邊際似然函數是在聯合似然函數的基礎上通過積分把能力θ積掉而得到。所以從本質上講, MEM通過積掉θ來控制能力的估計誤差。。所以, 在實踐中如果對運行時間有較高要求的話, 強烈建議選擇兩種新方法中表現相對更好的FFMLE-Method A作為在線標定方法; 否則, 建議使用MEM。 (2) 當CAT測驗長度較長(比如t=30)且樣本量較大(比如N=2000和3000)時, 建議使用總體表現最好且標定效率較高的ECSE-Method A; (3) 在CAT新題標定過程中融入新題參數的先驗信息, 能夠避免迭代算法不收斂的問題; (4) MEM的標定效率較高, 在不同條件下只需3至7次EM迭代就能滿足收斂標準; (5) 模擬的CAT可為被試提供準確的能力估計值。 Quellmalz和Pellegrino (2009)著重強調在線測驗在大規模評價項目中的重要作用, 比如國際學生評價項目(PISA)以及美國教育進展評估(NAEP)都計劃使用計算機施測或已經使用計算機呈現閱讀材料。目前美國已有超過27個州(包括Maryland、North Carolina和Oregon等)在州范圍或學期末的測驗中使用在線測驗形式。另外, 作為2001年美國小布什政府“不讓一個小孩掉隊” (No Child Left Behind)法案的擴展, 2009年奧巴馬政府頒布的“力爭上游” (Race to the Top)法案要求美國基礎教育階段(K-12)的州測評必須是計算機化的而且應該使用創新的題型。因此, 由23個州組成的共同體——“大學與職業準備測評聯盟” (Partnership for Assessment of Readiness for College and Career,PARCC)正在緊鑼密鼓地準備他們的在線州測評,而由另外25個州組成的“智能均衡測評聯盟”(Smarter Balanced Assessment Consortium, SBAC)也正在積極合作為其州測評設計CAT (Zheng,2014)。這些都為CAT中的在線標定技術提供了良好的發展前景。 Method A是最早提出的、最簡單的CAT在線標定方法。針對Method A的理論缺陷, 本文將FFMLE和ECSE與Method A相結合得到兩種新方法——FFMLE-Method A和ECSE-Method A, 它們借鑒FFMLE和ECSE的誤差校正思路從理論上對被試的能力估計誤差進行校正。為了考察兩種新方法的表現, 本研究在多種測驗情境下將它們與Method A (True)、Method A (Original)和MEM進行比較, 得到一些有意義的結果, 比如:(1)通過對能力估計誤差進行校正, 新方法在大多數實驗條件下總體上可以改進Method A的標定精度; (2)當CAT測驗長度較短(比如10題)時, 新方法對Method A的改進程度最大7由2.3節對兩種新方法的描述可知:當t→∞時, →, 因此當nj足夠大時, 兩種新方法的統計量具有優良統計特性。然而對于較短的測驗長度 (比如t=10), 上述假設會受到某種程度的違背,但這時新方法對Method A的改進程度最大, 一種可能的原因是:測驗較短時, CAT提供的能力估計精度較低, 留給改進的空間就比較大, 因此新方法通過校正能力估計誤差改進標定精度的幅度也較大;而違背上述假設受到的懲罰可能稍小一些。歡迎在今后的研究中對此有更為嚴格的解釋。; (3)由于考慮新題參數的先驗信息, 所有在線標定程序的N-R迭代全部收斂。但是,本文還存在一些不足值得今后進一步探討: 首先, 從嚴格意義上講, 所有在線標定方法(包括Method A)的標定精度都會受到題庫中舊題參數的估計誤差的影響。換句話說, 在構建CAT題庫時, 題庫中每個題目的參數都估計自某個標定樣本, 因此都存在某種程度的估計誤差(Cheng,2008)。這部分的誤差除了會傳遞到接下來的評分過程中, 對評分樣本的能力估計產生影響并低估能力估計的標準誤(Cheng & Yuan, 2010); 也會傳遞到MEM中E步和M步的相關計算中。本文提出的新方法(FFMLE-Method A和ECSE-Method A)在標定新題的過程中僅對能力估計誤差進行校正, 如果還能夠首先校正舊題參數的估計誤差(也即對兩類誤差都進行校正), 意義將不言而喻。另外, 本文討論的FFMLE和ECSE能否用于對舊題參數的估計誤差進行校正, 也有待進一步的研究。 其次, Chen等人(2012)將Method A推廣至認知診斷CAT (CD-CAT)領域(記為CD-Method A)。類似于Method A, CD-Method A也具有理論缺陷, 即將被試知識狀態(KS)估計值視為KS真值, 這樣KS的估計誤差也會傳遞到對新題的標定過程中。因此,今后值得研究的一個新方向是將FFMLE和ECSE應用于CD-Method A, 并對KS的估計誤差進行校正。需要指出的是, 不同于CAT中的待估能力是一維的連續變量, CD-CAT中待確定的KS是多維的二分離散變量, 這使得對KS估計誤差的校正會更加復雜。而且在DINA等認知診斷模型中, FFMLE和ECSE是否仍具有優良的統計特性也有待進一步的考證。另外, 汪文義、丁樹良和游曉鋒(2011)討論在CD-CAT測驗過程中植入新題時, 同樣考慮了KS的估計誤差, 并提出邊際MLE (MMLE)方法對屬性進行標定。Chen, Liu和Ying (2015)提出的“單個題目標定方法” (SIE)也考慮了KS估計的不確定性, 并成功應用于新題參數和新題屬性向量的同時估計。因此, 另一個有趣的問題是探索如何將MMLE和SIE方法應用于KS估計誤差的校正中。 再次, 盡管本文提出的兩種新方法能夠克服Method A的理論缺陷、并改進Method A的標定精度, 但是它們需要在較大樣本的前提下才能表現出較好的效果(也即當作答每個新題的被試數量nj=500和750時, 新方法的標定精度才開始突顯;與此對應的總被試樣本量N=2000和3000, 因為N=nj×(m C)且采用的是隨機在線標定設計), 而大樣本的收集在真實測驗情境中往往會比較困難,所以這是新方法的局限性之一。今后應當重點考慮如何在小樣本情境下改進Method A的標定缺陷。 最后, 為了討論方便本文僅考慮固定長度的CAT終止規則, 今后還可以在變化長度的CAT測驗情境中探討新方法FFMLE-Method A和ECSE-Method A相對于Method A和MEM的表現。另外, 在更為復雜的CAT測驗情境下考查FFMLE-Method A和ECSE-Method A的表現也是值得探索的研究方向, 比如能夠滿足題目曝光控制、內容均衡以及題目類型均衡等非統計約束條件的CAT、允許檢查并修改答案的CAT等。 Baker, F. B., & Kim, S. H. (2004).Item response theory: Parameter estimation techniques(2nded.). New York: Dekker. Ban, J.-C., Hanson, B. A., Wang, T. Y., Yi, Q., & Harris, D. J.(2001). A comparative study of on-line pretest item—calibration/scaling methods in computerized adaptive testing.Journal of Educational Measurement, 38(3), 191–212. Ban, J.-C., Hanson, B. A., Yi, Q., & Harris, D. J. (2002). Data sparseness and on-line pretest item calibration-scaling methods in CAT.Journal of Educational Measurement,39(3), 207–218. Birnbaum, A. (1968). Some latent trait models and their use in inferring an examinee’s ability. In F. M. Lord & M. R.Novick (Eds.),Statistical theories of mental test scores(pp.379–479). Reading, MA: Addison-Welsey. Carroll, R. J., Ruppert, D., Stefanski, L. A., & Crainiceanu, C.M. (2006).Measurement error in nonlinear models: A modern perspective(2nded.). London: Chapman and Hall. Chang, H. H. (2012). Making computerized adaptive testing diagnostic tools for schools. In R. W. Lissitz & H. Jiao(Eds.),Computers and their impact on state assessments:Recent history and predictions for the future(pp. 195–226).Charlotte, NC: Information Age. Chang, H. H. (2015). Psychometrics behind computerized adaptive testing.Psychometrika, 80(1), 1–20. Chang, H. H., Qian, J. H., & Ying, Z. L. (2001). a-stratified multistage computerized adaptive testing with b blocking.Applied Psychological Measurement, 25(4), 333–341. Chang, H. H., & Stout, W. (1993). The asymptotic posterior normality of the latent trait in an IRT model.Psychometrika,58(1), 37–52. Chang, Y.-C. I., & Lu, H. Y. (2010). Online calibration via variable length computerized adaptive testing.Psychometrika, 75(1),140–157. Chen, P. (2011).Item replenishing in cognitive diagnostic computerized adaptive testing——Based on DINA model(Unpublished doctorial dissertation). Beijing Normal University. [陳平. (2011).認知診斷計算機化自適應測驗的項目增補——以DINA模型為例(博士學位論文). 北京師范大學.] Chen, P., & Xin, T. (2011a). Developing on-line calibration methods for cognitive diagnostic computerized adaptive testing.Acta Psychologica Sinica, 43(6), 710–724. [陳平, 辛濤. (2011a). 認知診斷計算機化自適應測驗中在線標定方法的開發.心理學報, 43(6), 710–724.] Chen, P., & Xin, T. (2011b). Item replenishing in cognitive diagnostic computerized adaptive testing.Acta Psychologica Sinica, 43(7), 836–850. [陳平, 辛濤. (2011b). 認知診斷計算機化自適應測驗中的項目增補.心理學報, 43(7), 836–850.] Chen, P., & Xin, T. (2014).A new online calibration approach for multidimensional computerized adaptive testing. Paper presented at the National Council on Measurement in Education, Philadelphia, PA. Chen, P., Xin, T., Wang, C., & Chang, H. H. (2012). Online calibration methods for the DINA model with independent attributes in CD-CAT.Psychometrika, 77(2), 201–222. Chen, P., Zhang, J. H., & Xin, T. (2013). Application of online calibration technique in computerized adaptive testing.Advances in Psychological Science, 21(10), 1883–1892. [陳平, 張佳慧, 辛濤. (2013). 在線標定技術在計算機化自適應測驗中的應用.心理科學進展, 21(10), 1883–1892.] Chen, Y. X., Liu, Y. C., & Ying, Z. L. (2015). Online item calibration for Q-matrix in CD-CAT.Applied Psychological Measurement, 39(1), 5–15. Cheng, Y. (2008).Computerized adaptive testing – new developments and applications(Unpublished doctorial dissertation). University of Illinois at Urbana-Champaign. Cheng, Y., & Yuan, K. H. (2010). The impact of fallible item parameter estimates on latent trait recovery.Psychometrika,75(2), 280–291. Clark, R. R. (1982).The errors-in-variables problem in the logistic regression model(Unpublished doctorial dissertation).University of North Carolina, Chapel Hill. Flaugher, R. (2000). Item pools. In H. Wainer, N. J. Dorans, R.Flaugher, B. F. Green, & R. J. Mislevy (Eds.),Computerized adaptive testing: A primer(Chap.3, 2nded., pp. 37–59).Mahwah, NJ: Erlabum. Guo, F. M., & Wang, L. (2003).Online calibration and scale stability of a CAT program. Paper presented at the annual meeting of National Council on Measurement in Education,Chicago, IL. Jones, D. H., & Jin, Z. Y. (1994). Optimal sequential designs for on-line item estimation.Psychometrika, 59(1), 59–75. Lien, D.-H. D. (1985). Moments of truncated bivariate lognormal distributions.Economics Letters, 19(3), 243–247. Lord, F. M. (1980).Applications of item response theory to practical testing problems. Hillside, NJ: Erlbaum. Mislevy, R. J. (1986). Bayes modal estimation in item response models.Psychometrika, 51(2), 177–195. Parshall, C. G. (1998).Item development and pretesting in a computer-based testing environment. Paper presented at the colloquium Computer-Based Testing: Building the Foundation for Future Assessments, Philadelphia, PA. Qi, S. Q., Dai, H. Q., & Ding, S. L. (2002).Principles of modern educational and psychological measurement. Beijing,China: Higher Education Press. [漆書青, 戴海琦, 丁樹良. (2002).現代教育與心理測量學原理. 北京: 高等教育出版社.] Quellmalz, E. S., & Pellegrino, J. W. (2009). Technology and Testing.Science, 323(5910), 75–79. Stefanski, L. A., & Carroll, R. J. (1985). Covariate measurement error in logistic regression.Annals of Statistics, 13(4),1335–1351. Stocking, M. L. (1988).Scale drift in on-line calibration(Research Rep. 88–28). Princeton, NJ: ETS. Tian, J. Q., Miao, D. M., Yang, Y. B., He, N., & Xiao, W.(2009). The development of computerized adaptive picture assembling test for recruits in China.Acta Psychologica Sinica, 41(2), 167–174. [田健全, 苗丹民, 楊業兵, 何寧, 肖瑋. (2009). 應征公民計算機自適應化拼圖測驗的編制.心理學報, 41(2), 167–174.] van der Linden, W. J., & Ren, H. (2015). Optimal Bayesian adaptive design for test-item calibration.Psychometrika,80(2), 263–288. Wainer, H., Dorans, N. J., Flaugher, R., Green, B. F., Mislevy, R.J., Steinberg, L., & Thissen, D. (1990).Computerized adaptive testing: A primer. Hillsdale, NJ: Lawrence Erlbaum. Wainer, H., & Mislevy, R. J. (1990). Item response theory,item calibration, and proficiency estimation. In H. Wainer,N. J. Dorans, R. Flaugher, B. F. Green, R. J. Mislevy, L.Steinberg, & D. Thissen (Eds.),Computerized adaptive testing: A primer(Chap. 4, pp. 65–102). Hillsdale, NJ:Erlbaum. Wang, C. (2012).Semi-parametric models for response times and response accuracy in computerized testing(Unpublished doctorial dissertation). University of Illinois at Urbana-Champaign. Wang, W. Y., Ding, S. L., & You, X. F. (2011). On-line item attribute identification in cognitive diagnostic computerized adaptive testing.Acta Psychologica Sinica, 43(8), 964–976. [汪文義, 丁樹良, 游曉鋒. (2011). 計算機化自適應診斷測驗中原始題的屬性標定.心理學報, 43(8), 964–976.] Weiss, D. J. (1982). Improving measurement quality and efficiency with adaptive testing.Applied Psychological Measurement, 6(4), 473–492. You, X. F., Ding, S. L., & Liu, H. Y. (2010). Parameter estimation of the raw item in computerized adaptive testing.Acta Psychologica Sinica, 42(7), 813–820. [游曉鋒, 丁樹良, 劉紅云. (2010). 計算機化自適應測驗中原始題項目參數的估計.心理學報, 42(7), 813–820.] Zheng, Y. (2014).New methods of online calibration for item bank replenishment(Unpublished doctorial dissertation).University of Illinois at Urbana-Champaign.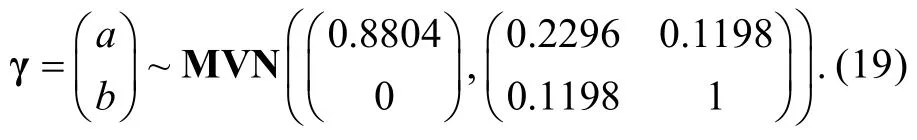
3.2 新題生成
3.3 CAT全過程模擬程序描述
3.4 在線標定實施程序描述
3.4.1 在線標定設計描述
3.4.2 在線標定方法實施程序描述
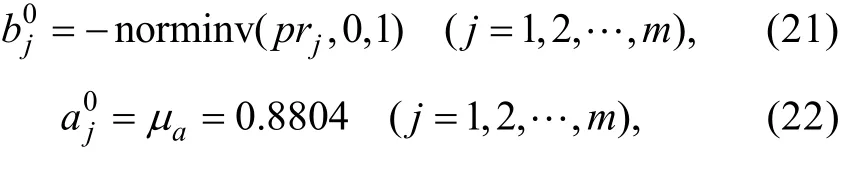
3.5 評價指標
3.5.1 均方根誤差
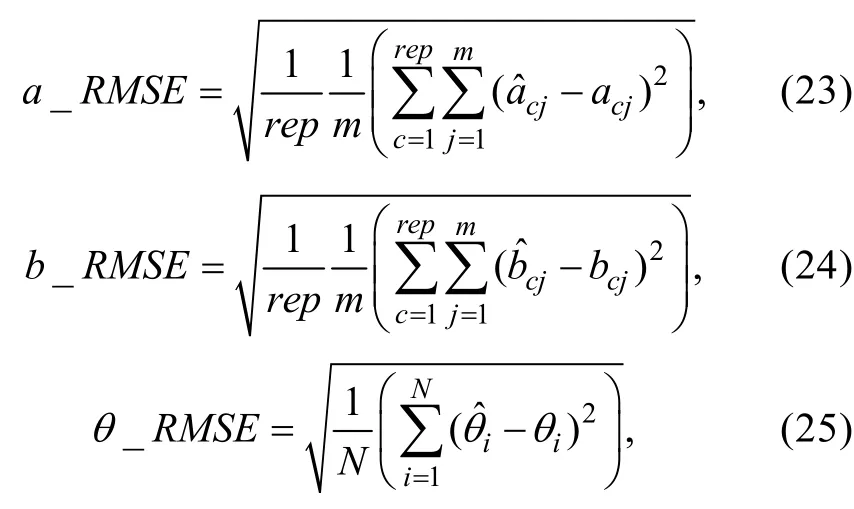
3.5.2 偏差

3.5.3 加權的均方誤差
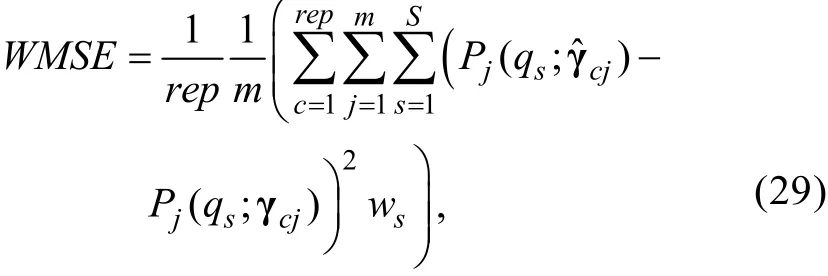
3.5.4 最小/最大/平均EM循環次數
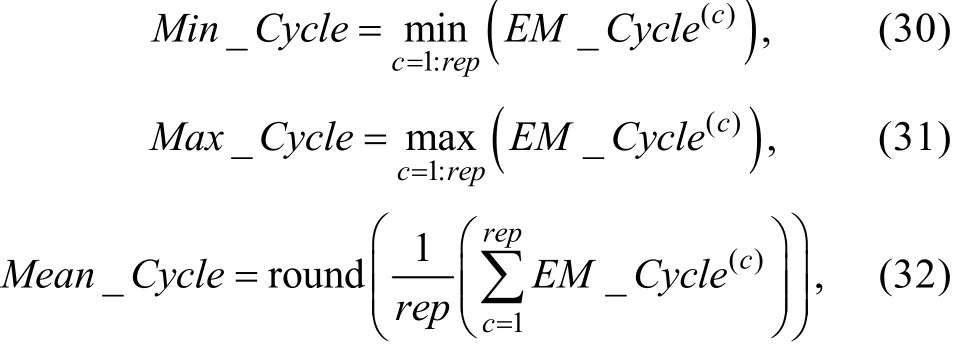
3.5.5 平均程序運行時間

4 結果與結論
4.1 結果
4.1.1 CAT的能力估計精度
4.1.2 在線標定方法的標定精度


4.1.3 在線標定方法的標定效率


4.2 結論
5 討論及今后的研究方向

