高寬比較大的扣件式鋼管腳手架整體穩(wěn)定性研究及應(yīng)用

張家賢，李開福，張?jiān)獫瑴狼?/p>

(1.湖南大學(xué)建筑學(xué)院，長沙 410010； 2.云南建工第四建設(shè)有限公司，云南 曲靖 655002；3.中南大學(xué)圖書館，長沙 410010)

高寬比較大的扣件式鋼管腳手架整體穩(wěn)定性研究及應(yīng)用

張家賢1，2，李開福2，張?jiān)獫?，湯道清3

(1.湖南大學(xué)建筑學(xué)院，長沙 410010； 2.云南建工第四建設(shè)有限公司，云南 曲靖 655002；3.中南大學(xué)圖書館，長沙 410010)

分析了高寬比較大的扣件式鋼管腳手架的受力特點(diǎn)，用彈簧單元替代直角扣件這種特殊的半剛性連接方式，引入彈簧單元的伸縮系數(shù)及轉(zhuǎn)動剛度，建立了線彈性格構(gòu)式柱計(jì)算模型，利用半剛性連接的鋼框架模型計(jì)算單位水平力作用下層間相對位移，推導(dǎo)出該模型的失穩(wěn)屈曲荷載計(jì)算公式。對高寬比等于27.3的扣件式鋼管腳手架，采用MIDAS GEN有限元軟件建立模型進(jìn)行數(shù)值分析，獲取失穩(wěn)屈曲荷載值，并對比簡化計(jì)算結(jié)果，可知公式的計(jì)算精度能滿足工程設(shè)計(jì)及校核的需要。

扣件式腳手架；半剛性；伸縮系數(shù)；轉(zhuǎn)動剛度；鋼框架；線彈性；失穩(wěn)；有限元

0 引言

倉筒結(jié)構(gòu)一般采用滑模技術(shù)施工，在施工過程中，上人專用斜道一般采用扣件式鋼管體系搭設(shè)，該體系裝拆方便，經(jīng)濟(jì)適用，是臨時(shí)受力結(jié)構(gòu)的最佳選擇。由于倉筒結(jié)構(gòu)較高，相應(yīng)的上人斜道的高寬比較大。JGJ130—2011《建筑施工扣件式鋼管腳手架安全技術(shù)規(guī)范》中所規(guī)定的整體穩(wěn)定性驗(yàn)算是基于受壓桿的歐拉公式來計(jì)算的，計(jì)算假設(shè)與此類結(jié)構(gòu)體系的實(shí)際受力不相符，對于此類超高且高寬比較大的扣件式腳手架的穩(wěn)定性暫無統(tǒng)一的計(jì)算公式。為此，筆者對云南曲靖雄業(yè)水泥廠60 m高倉筒上人專用通道扣件式鋼管腳手架進(jìn)行了受力分析，建立整體穩(wěn)定性計(jì)算公式。并采用MIDAS GEN有限元軟件建立結(jié)構(gòu)模型，通過數(shù)值分析求解失穩(wěn)屈曲荷載值來驗(yàn)證計(jì)算公式的可用性。

1 計(jì)算模型

1.1 搭設(shè)方案

小橫桿、大橫桿、立桿、剪刀撐鋼管均采用Q235級Φ48 mm×3.0 mm，縱橫方向采用直角扣件與立桿連接，剪刀撐采用旋轉(zhuǎn)扣件與小橫桿連接，搭設(shè)如圖1～2所示。

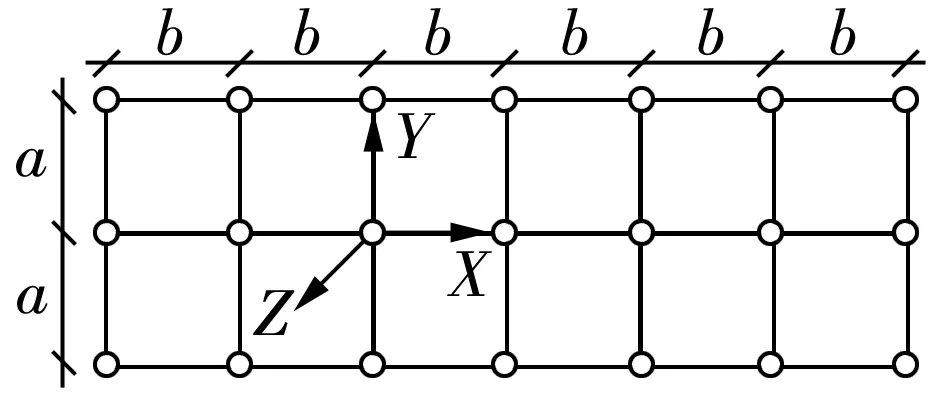
圖1 扣件式鋼管腳手架平面圖

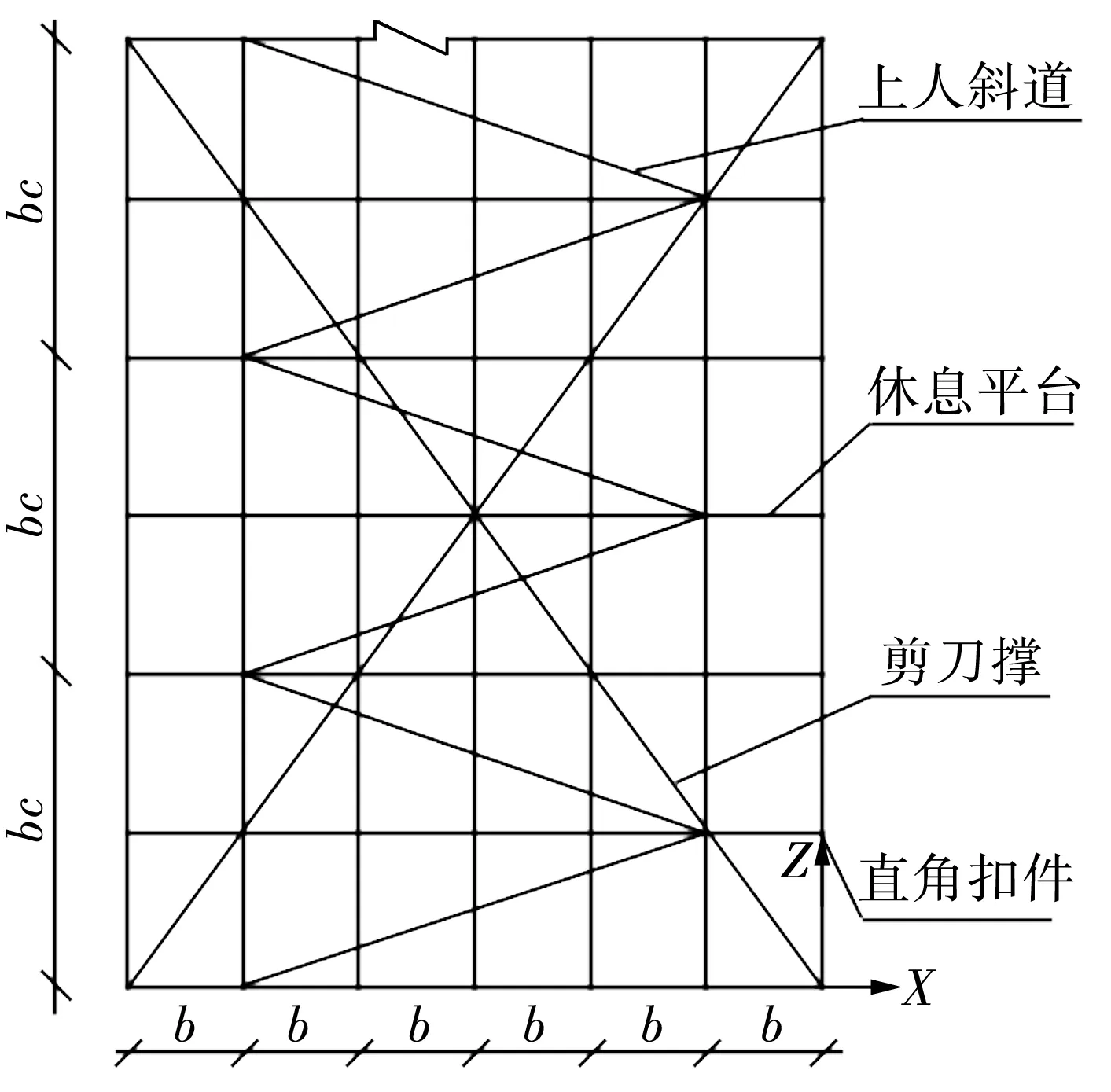
圖2 扣件式鋼管腳手架立面圖

1.2 受力分析

扣件式鋼管腳手架由立桿、小橫桿、大橫桿、腳手板、剪刀撐構(gòu)成。受力傳遞順序：腳手板→小橫桿→立桿→底座→基礎(chǔ)，小橫桿的力是不需要傳遞給大橫桿然后到立桿的，直接通過直角扣件，小橫桿可將力傳遞到立桿。在XZ平面內(nèi)，由連續(xù)的豎向剪刀撐連接，且X方向立桿排數(shù)較Y方向多，其側(cè)向位移很小，大橫桿與立桿通過直角扣件連接，連接可視為剛節(jié)點(diǎn)，X方向的立桿的剛度較Y方向大。在YZ平面內(nèi)，Y方向有連墻件作為支座，但是該方向無法設(shè)置連續(xù)的豎向剪刀撐，且立桿排數(shù)較少，Y方向的剛度較小。

1.3 計(jì)算模型

由于采用腳手架空間結(jié)構(gòu)模型難以通過解析法求得結(jié)構(gòu)的失穩(wěn)臨界荷載，因此本文采用簡化計(jì)算方法，把整體空間工作的力學(xué)模型簡化為平面模型。在整個(gè)扣件式鋼管腳手架空間體系中文獻(xiàn)[1]分析大橫桿與立桿連接節(jié)點(diǎn)可視為剛接，其余直角扣件及旋轉(zhuǎn)扣件均簡化為半剛性節(jié)點(diǎn)，受力體系中主要簡化為兩種平面模型[1]：一種是在XZ平面，整體穩(wěn)定性研究可簡化為剛性連接無側(cè)位移的鋼框結(jié)構(gòu)計(jì)算單元(圖3(a))，立桿與大橫桿、剪刀撐組成鋼框架結(jié)構(gòu)；另一種在YZ平面，整體穩(wěn)定性研究可簡化為半剛性、鉸支座約束的綴板格構(gòu)式柱計(jì)算單元(圖3(b))，格構(gòu)柱以立桿為肢件，大橫桿為橫綴板。對于XZ平面，扣件式鋼管腳手架結(jié)構(gòu)失穩(wěn)形式表現(xiàn)為繞Y軸失穩(wěn)。而縱向鋼框架具有較多的跨數(shù)，其剛度一般較大，因而，扣件式鋼管腳手架平面外失穩(wěn)破壞的承載力高于平面內(nèi)失穩(wěn)破壞，該結(jié)構(gòu)體系的穩(wěn)定性研究不考慮平面外失穩(wěn)。比較兩平面的剛度，顯然，XZ平面的剛度比YZ平面大，扣件式腳手架體系的整體失穩(wěn)應(yīng)在YZ平面內(nèi)發(fā)生。

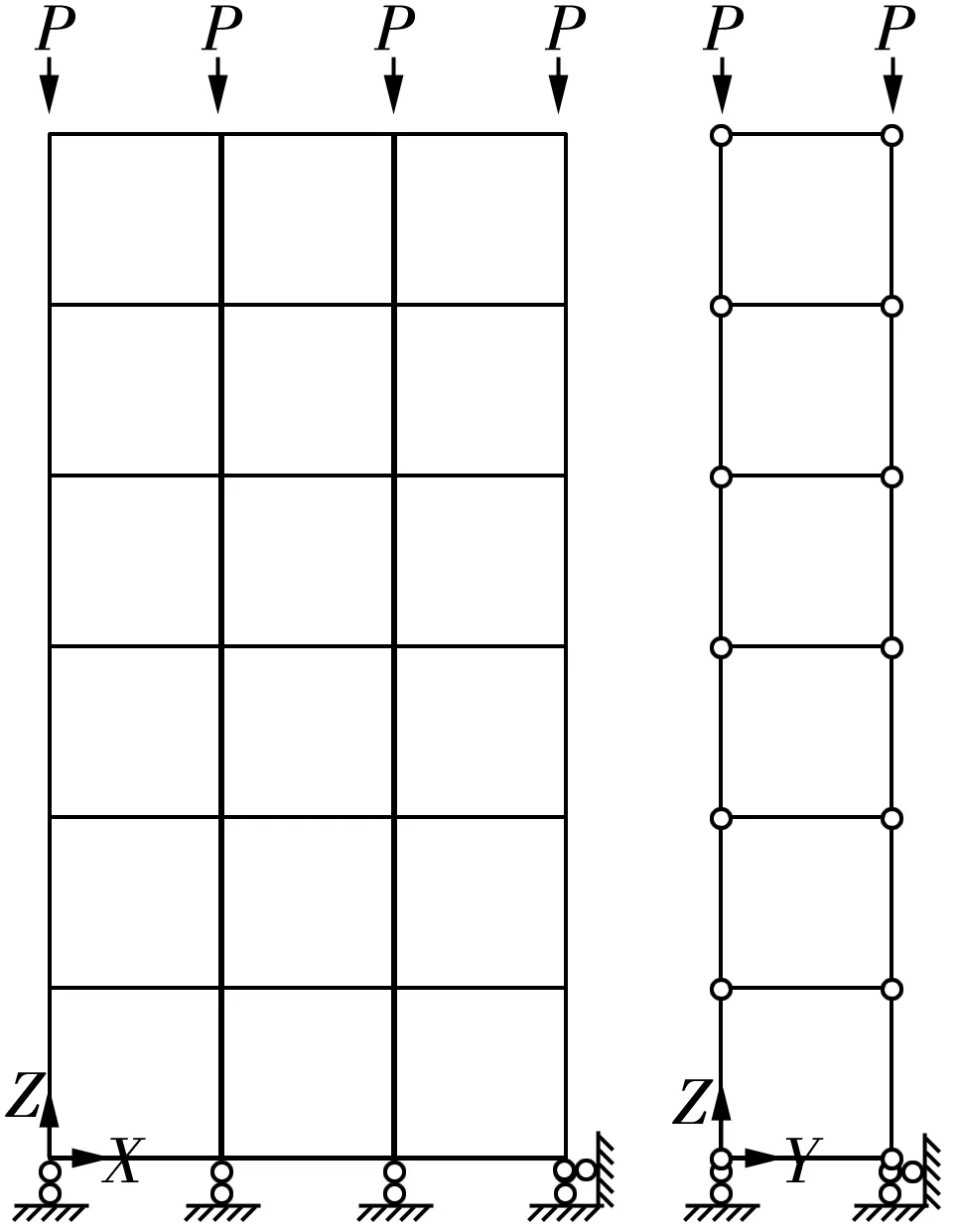
(a)XZ平面 (b)YZ平面圖3 平面模型

1.4 計(jì)算假設(shè)

在進(jìn)行計(jì)算分析時(shí)，作如下假設(shè)：

1)假設(shè)材料為理想的彈性材料，不考慮材料非線性的影響。由試驗(yàn)結(jié)果可知腳手架的穩(wěn)定極限應(yīng)力一般低于鋼材的彈性極限，因而這一假設(shè)能滿足工程建設(shè)的精度要求；

2)不考慮半剛性連接的非線性性能，半剛性節(jié)點(diǎn)的線性節(jié)點(diǎn)轉(zhuǎn)角本構(gòu)關(guān)系[2]：

M=kθ；

3)剪切變形僅考慮半剛性節(jié)點(diǎn)的影響，由于桿件的線性伸縮值很小，忽略桿件的彈性應(yīng)變。

4)以實(shí)腹等效立桿及實(shí)腹等效橫桿代替實(shí)際的扣件式鋼管腳手架結(jié)構(gòu)以簡化計(jì)算。

5)連墻件按照一步三跨設(shè)置，格構(gòu)式柱為超靜定結(jié)構(gòu)，為簡化計(jì)算和加強(qiáng)安全儲備值，假定格構(gòu)式柱為兩端鉸支承。

2 扣件式鋼管腳手架體系中綴板格構(gòu)式柱的穩(wěn)定計(jì)算[3]

2.1 軸心受壓實(shí)心柱整體穩(wěn)定臨界荷載

圖4所示兩端鉸支等截面實(shí)腹桿,在壓力P的作用下達(dá)到臨界值后發(fā)生屈曲,設(shè)某一截面的撓度為y,這一變形由彎矩和剪力共同作用產(chǎn)生。設(shè)yM是由彎矩M引起的撓度,yQ是由剪力Q引起的撓度,則:

y=yM+yQ。

(1)

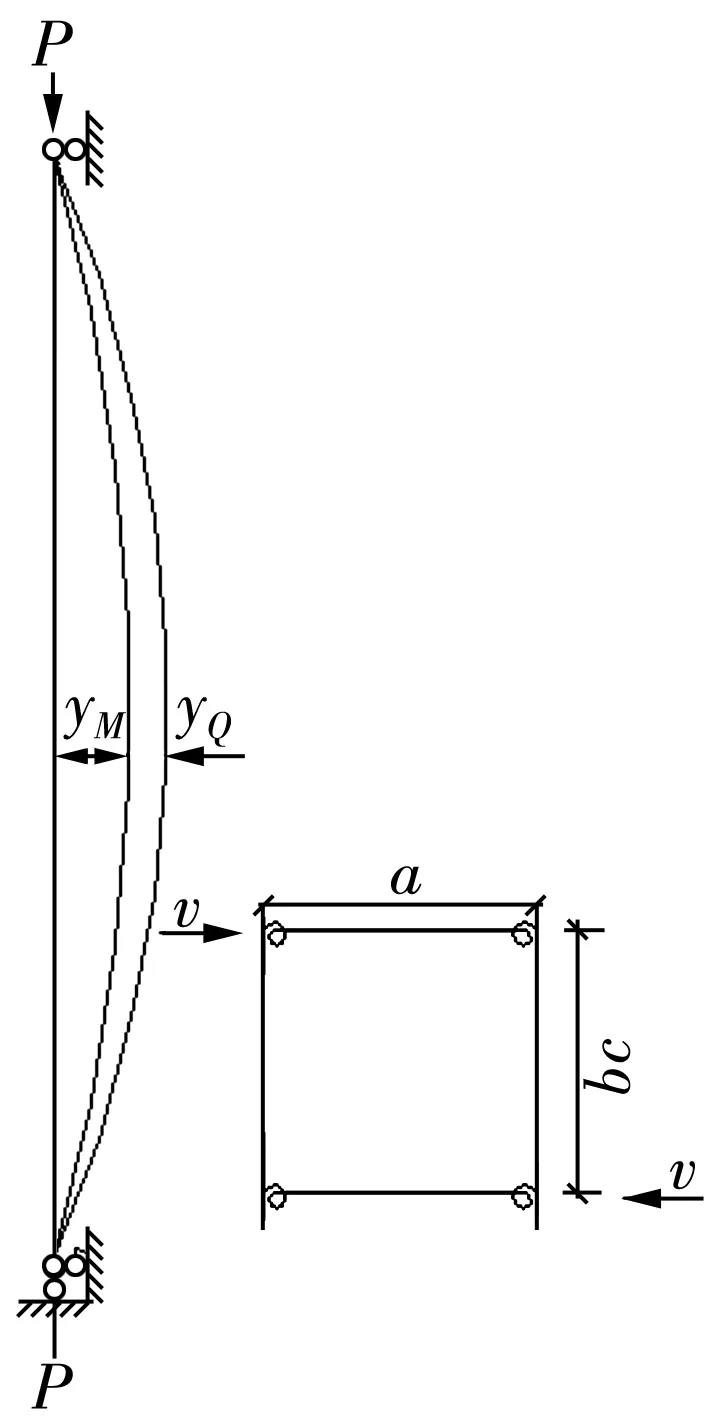
圖4 兩端鉸支實(shí)腹式受壓桿

將式(1)對高度z微分兩次，得彎矩和剪力共同作用下的彈性曲線微分方程：

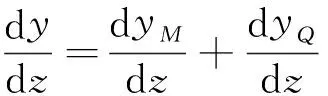
(2)

實(shí)腹柱在荷載P的作用下，考慮小變形情況，根據(jù)材料力學(xué)，彎矩影響產(chǎn)生的曲率：

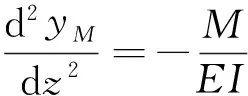
(3)

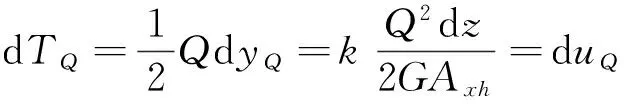
(4)

式中：M為荷載P作用下產(chǎn)生的彎矩；EI為實(shí)腹桿的抗彎剛度。

剪切影響產(chǎn)生的附加曲率，在圖4中所示的坐標(biāo)系中，根據(jù)能量原理[4]，可知剪力Q做的微元功dTQ在數(shù)值上等于剪切變形所儲存的微元變形能duQ,于是

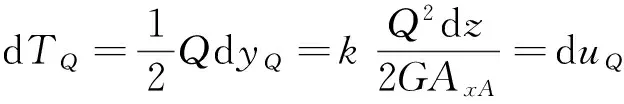
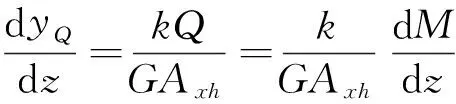
(5)

式中：k為截面形狀系數(shù)；G為剪切模量；AxA為桿件截面面積。

將式(5)對z微分一次，可得由剪力Q引起的曲率：

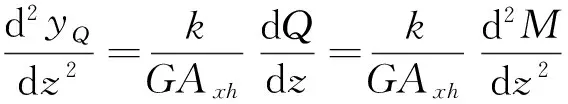
(6)

任意截面的彎矩M=py，相應(yīng)

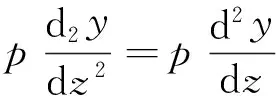
(7)

將式(3)～式(7)代入式(2)，整理可得

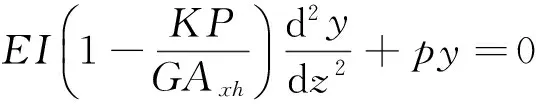
(8)

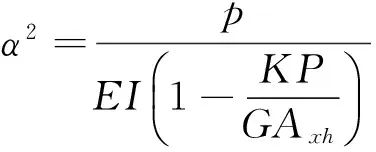
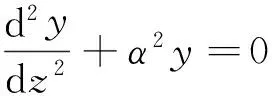
(9)

式(9)為二階常系數(shù)線性微分方程，其通解為

y=Asinαz+Bcosαz。

(10)

圖4中，邊界條件1)z=0，y=0；2)z=L,y=0，代入式(10)，比較系數(shù)，解齊次線性方程組，其系數(shù)A、B的行列式等于0，解得

αL=nπ (n=1,2,3……)。

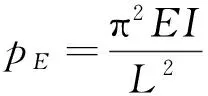
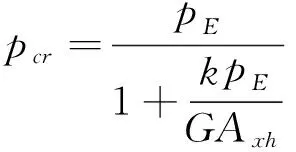
(11)

式中：pE為歐拉臨界荷載；pcr為考慮剪力的臨界荷載。

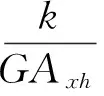
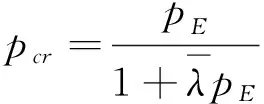
(12)

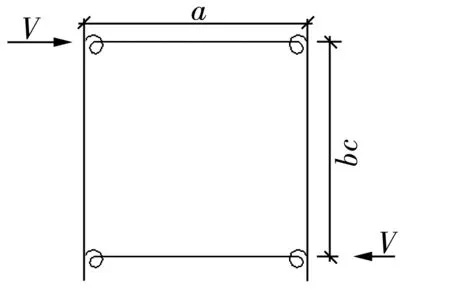
圖5 剪力作用單元

如圖5所示，直角扣件的連接簡化為半剛性彈簧單元，由GB 15831—2006《鋼管腳手架扣件規(guī)范》[5]的抗滑移試驗(yàn)可知，當(dāng)P=7 kN時(shí)，Δ1≤7 mm；當(dāng)P=10 kN時(shí)，Δ2≤5 mm；由扭轉(zhuǎn)剛度性能試驗(yàn)，可知M=900 N·m時(shí)，θ≤4°。引入伸縮系數(shù)k1和轉(zhuǎn)動剛度k2。

1)伸縮系數(shù)k1(mm/N)——單位力作用下扣件的位移

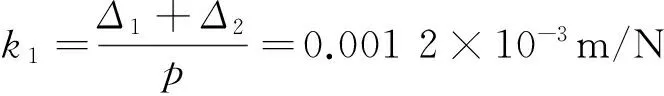
(13)

鋼框計(jì)算單元中由4個(gè)直角扣件構(gòu)成，其相對位移：

δ1=4k1。

(14)

2)由文獻(xiàn)[6],取k2=15 170 N·m/rad，圖5中豎向單元在單位力作用下的側(cè)向位移，可簡化為計(jì)算半剛性連接的鋼框架豎向柱在水平力作用下的層間位移[7]。基于圖6以柱AB為計(jì)算單元，并作如下假設(shè)：

1)AB柱、AC柱及BD柱水平側(cè)移值δ相等，且θA=θB=θC=θD；

2)直角扣件轉(zhuǎn)動剛度k2=15 170 N·m/rad；

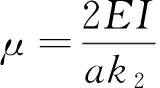
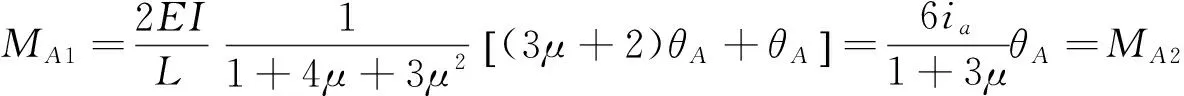
(15)

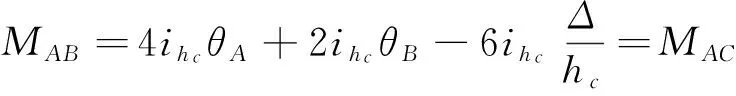
(16)

(17)

同理，根據(jù)節(jié)點(diǎn)B彎矩平衡條件得：

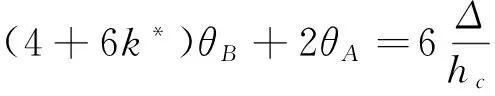
(18)

聯(lián)立式(17)、式(18)解得轉(zhuǎn)角：

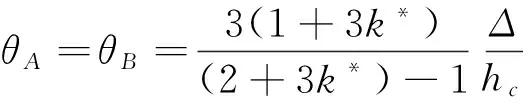
(19)

柱AB的剪力可得

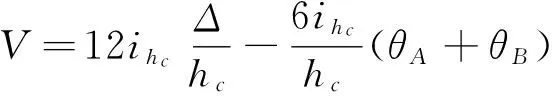
(20)

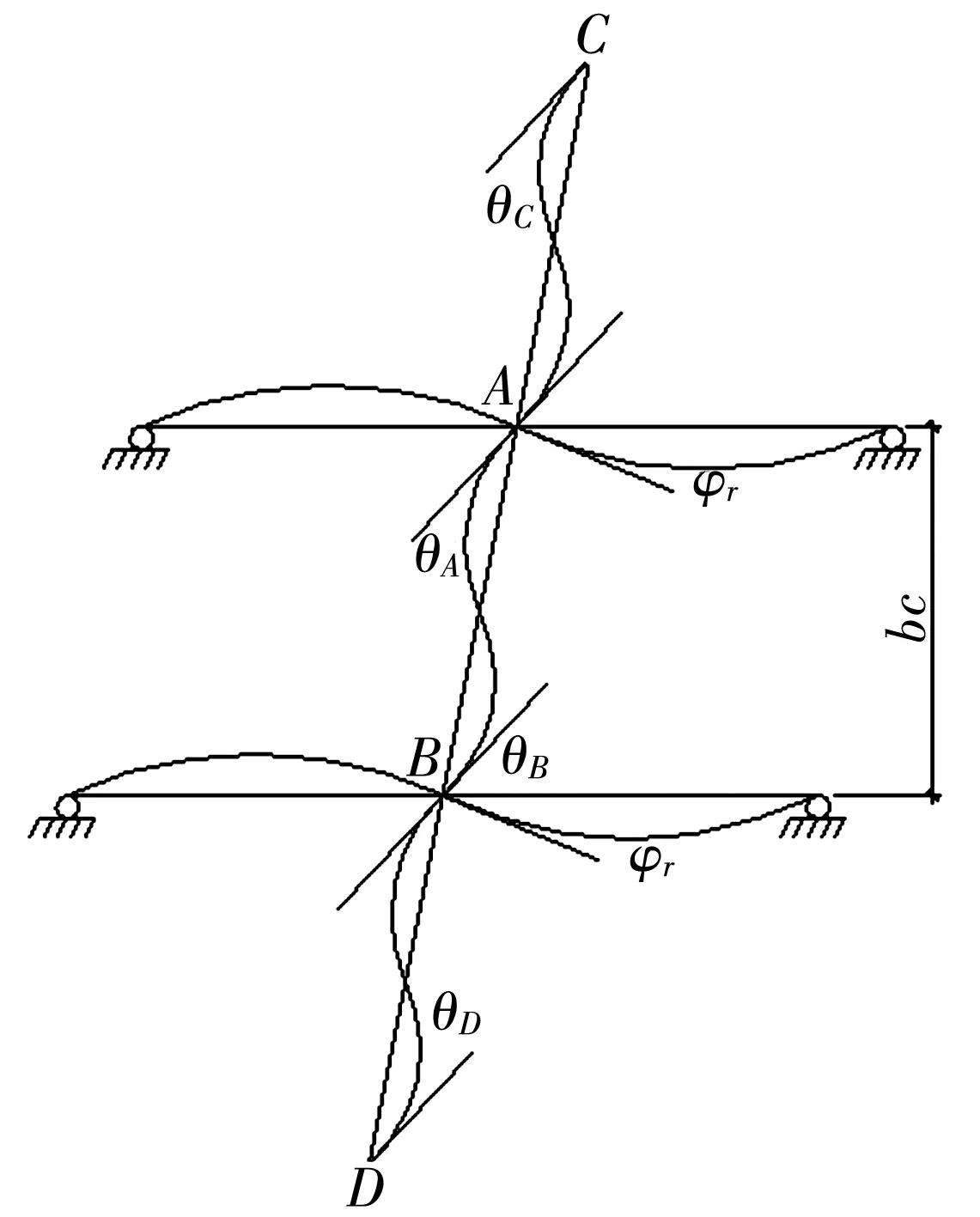
圖6 鋼框架側(cè)向位移桿件材料

將式(19)代入式(20)并令剪力Δ=1時(shí)，可得抗側(cè)移剛度，層間水平位移為抗剪剛度的導(dǎo)數(shù)，即：

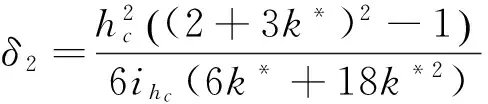
(21)

圖5單元的總位移：

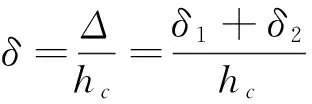
(22)

經(jīng)比較δ1遠(yuǎn)遠(yuǎn)小于δ1，故

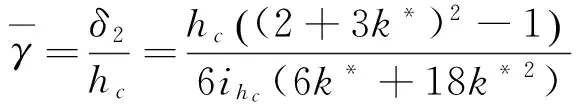
(23)

3 扣件式鋼管腳手架體系中綴板格構(gòu)式柱穩(wěn)定計(jì)算的應(yīng)用

云南曲靖雄業(yè)水泥廠60m高倉筒上人專用通道扣件式鋼管腳手架，搭設(shè)參數(shù)：a=1 100 mm，b=1 200 mm，hc=3 000 mm，L=60 m，Q235級Ф48×3鋼管，則形常數(shù)A=424 mm2，E=206 000 N/mm2，Ixc=107 800 mm4，Ix=12 367 800 mm2，PE=72 423 N。

則可求得：

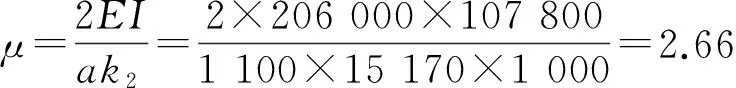
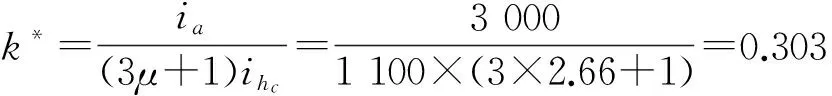
0.000 072。

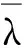
上述pcr不含扣件鋼管的自重，格構(gòu)式肢件所承載的自重為：m=((2.2×21)/3+1.2×21+60)×3.84+1.3×21=413.33kg，G=289.54×9.8=4 050.634N。故格構(gòu)式扣件鋼管腳手架單立桿的屈曲極限荷載為7 611.67N。

4 扣件式鋼管腳手架線彈性屈曲分析

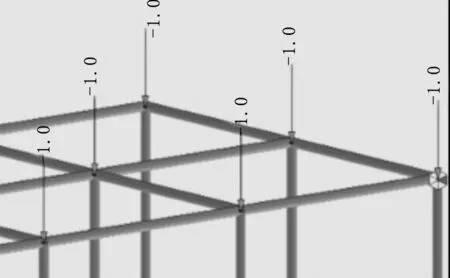
圖7 加載位置

圖8 屈曲模態(tài)

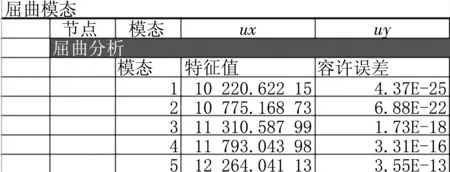
圖9 特征值

5 結(jié)語

通過上述的分析及計(jì)算對比，可得以下結(jié)論：

1)扣件式腳手架的層間錯(cuò)動位移由扣件的轉(zhuǎn)動產(chǎn)生的水平位移和扣件的滑移構(gòu)成，在穩(wěn)定性計(jì)算中，單位剪力作用下的層間位移主要取決于扣件的轉(zhuǎn)動產(chǎn)生的線位移，扣件的滑移值可忽略不計(jì)。

2)高寬比較大的扣件式腳手架的連墻件對結(jié)構(gòu)的屈曲荷載值是有貢獻(xiàn)的，且貢獻(xiàn)值可作為扣件式鋼管腳手架的安全儲備值。

3)高寬比較大的扣件式腳手架的穩(wěn)定性計(jì)算可簡化為兩端簡支的格構(gòu)式柱計(jì)算，層間位移可簡化為半剛性節(jié)點(diǎn)的鋼框架計(jì)算，其計(jì)算值的精度可滿足工程設(shè)計(jì)及校核的需要。

[1] 劉希月.門式鋼管腳手架穩(wěn)定性承載力的穩(wěn)定理論分析[J].建筑科學(xué),2013,29(3):32-36.

[2] 張紅衛(wèi).基于整架試驗(yàn)的扣件式鋼管腳手架半剛性節(jié)點(diǎn)計(jì)算方法[D].濟(jì)南：山東建筑大學(xué)，2009.

[3] 陳紹蕃.鋼結(jié)構(gòu)穩(wěn)定設(shè)計(jì)指南[M].北京：中國建筑工業(yè)出版社，2004.

[4] 陳驥.鋼結(jié)構(gòu)穩(wěn)定理論與設(shè)計(jì)[M].北京：科學(xué)出版社,2001.

[5] 中國標(biāo)準(zhǔn)出版社.GB 15831—2006鋼管腳手架扣件規(guī)范[S].北京：中國標(biāo)準(zhǔn)出版社，2006.

[6] 敖鴻斐,李國強(qiáng).雙排扣件式鋼管腳手架的極限穩(wěn)定承載力研究[J].力學(xué)季刊，2004,25(2):213-218.

[7] 胡習(xí)兵.半剛性連接鋼框架的簡化計(jì)算方法[D].長沙：湖南大學(xué),2005.

[8] 陳惠發(fā).鋼框架穩(wěn)定設(shè)計(jì)[M].周綏平，譯.上海:世界圖書出版公司,1999：264-381.

[9] 薛德明,戴仁杰.計(jì)算結(jié)構(gòu)力學(xué)[M].上海:同濟(jì)大學(xué)出版社,1988.

The Application Research on Overall Stability of Steel Tubular Scaffolding with a Great Aspect Tatio

ZHANG Jia-xian，et al.

(SchoolofArchitecture,HunanUniversity,Changsha410010,China)

In this article，the features of forces applied on steel tubular scaffolds with couplers which have greater aspect ratio are researched.The linear spring lattice column computing model is established with a special semi-rigid connection that spring elements are used to replace right-angle couplers and by introducing the telescopic coefficient and rotating rigidity of the spring unit.Under a unit horizontal force，the relative displacement between two layers is calculated with semi-rigidly connected steel frame model，and，the formula is deduced for calculating the buckling loads of this model.And，the modeling is made for value analysis to attain the values of buckling loads with MIDAS GEN finite elements software based on steel tubular scaffolds with couplers with an aspect ratio of 27.3.By comparison to the results of the simplified calculation，the calculating accuracy of the formula may meet the needs of engineering design and verification.

fastener type scaffolding；semi rigid；telescopic coefficient；rotational rigidity；steel frame；linear elasticity；instability；finite element

10.3969/j.issn.1009-8984.2016.04.004

2016-05-24

張家賢(1985-)，男(漢)，云南曲靖，碩士，工程師 主要研究混凝土及鋼結(jié)構(gòu)。

TU393

A

1009-8984(2016)04-0011-05