粒子濾波算法在視頻目標跟蹤中的應用

付浩海，柯洪昌

(長春工程學院計算機技術與工程學院，長春 130012)

粒子濾波算法在視頻目標跟蹤中的應用

付浩海，柯洪昌

(長春工程學院計算機技術與工程學院，長春 130012)

首先介紹粒子濾波的基本理論，然后構建粒子濾波視頻目標跟蹤系統的狀態模型和觀測模型，進而根據狀態模型和觀測模型提出一種基于粒子濾波的視頻目標跟蹤算法，并通過實際的視頻目標跟蹤系統對算法進行實驗分析，說明粒子濾波算法在視頻目標跟蹤中的優越性。

貝葉斯濾波；粒子濾波；視頻目標跟蹤；算法應用

0 引言

粒子濾波是一種基于蒙特卡羅方法和遞推貝葉斯估計的統計濾波方法，它依據大數定律，采用蒙特卡羅方法求解貝葉斯估計中的積分運算。一般情況下，粒子代表運動過程中的一種可能情況，也即一種狀態；而濾波則是對目標的當前狀態進行估計。在估計理論中，粒子濾波表示利用目標的觀測數據及前一時刻的后驗概率密度來估計目標的當前后驗概率密度。也就是通過非參數化的蒙特卡羅模擬方法來實現遞推貝葉斯濾波，相對于卡爾曼濾波體系，該方法可用于各種能用狀態空間模型表示的非線性系統，其估計精度可以逼近最優估計。一般來說，粒子濾波以蒙特卡羅模擬方法來實現遞推貝葉斯濾波的計算量大于卡爾曼濾波等數學方程求解形式，但隨著并行計算技術的發展和計算機硬件性能的提高，使得粒子濾波逐漸成為一種更具實用價值的濾波技術，應用也越來越廣泛。而視頻圖像序列中的運動目標跟蹤問題，恰好可以看作是根據目標的一系列觀測值(即前面各幀的目標信息)來估計當前幀目標的位置的問題。

本文首先介紹粒子濾波的基本理論，然后構建粒子濾波視頻目標跟蹤的狀態模型和觀測模型，進而根據狀態模型和觀測模型提出一種基于粒子濾波的視頻目標跟蹤算法，并通過實際的視頻目標跟蹤系統對算法進行實驗分析，說明粒子濾波算法在視頻目標跟蹤中的優越性。

1 粒子濾波算法原理

1.1 貝葉斯濾波

一般情況下，非線性動態系統或目標跟蹤系統可以用下面的狀態方程和觀測方程來描述：

狀態方程：xk=fk(xk-1,vk)，

(1)

觀測方程：zk=gk(xk,nk)。

(2)

式中：k∈N為離散時間；xk∈Rn為時刻的系統狀態向量，在目標跟蹤系統中可以是由目標位置、目標速度等構成的向量；fk:Rn×Rn→Rn為狀態轉移函數；{vk}k∈N為獨立同分布的過程噪聲序列；zk∈Rm為k時刻的觀測量；gk:Rn×Rm→Rm為觀測函數；{nk}k∈N為獨立同分布的觀測噪聲序列。

假定初始先驗概率密度函數已知，表示為ρ(x0|z0)=p(x0)，于是粒子濾波算法可以敘述為：依據所有測量值集合z1∶k={zi∶i=1，2，…，k}，給出對狀態xk的估計。因此，問題就轉化為如何依據集合z1∶k，求后驗概率密度ρ(xk|z1∶k)，這恰好可以借助貝葉斯濾波實現。貝葉斯濾波的實質是用系統模型預測狀態變量的先驗概率密度ρ(xk|z1∶k-1)，再根據觀測值進行更新修正，估計系統狀態變量的后驗概率密度函數ρ(xk|z1∶k)。貝葉斯濾波是由預測和更新兩部分遞歸實現的。

預測：ρ(xk|z1∶k-1)=∫ρ(xk|xk-1)ρ(xk-1|z1∶k-1)dxk-1，

(3)

式中利用了一階馬爾科夫過程性質：ρ(xk|xk-1，z1∶k-1)=ρ(xk|xk-1)。

(4)

在實際中利用式(3)和(4)求解概率密度函數是很難實現的，因為需要計算多重積分，而且求解后驗概率密度函數并不是我們的最終目的，我們希望通過這個后驗概率密度得到服從這個概率密度分布的某個隨機變量的函數的估計值(期望或方差等)。因此，人們引入了蒙特卡羅方法來求解貝葉斯濾波，即得到了粒子濾波(或稱為序貫蒙特卡羅濾波)。

1.2 粒子濾波

粒子濾波的核心思想是：首先依據系統狀態向量的經驗條件分布，在狀態空間產生一組隨機樣本集合(粒子)，然后根據量測不斷調整粒子的權重與位置，通過調整后的粒子信息修正最初的經驗條件分布。其實質是用粒子及其權重組成的離散隨機測度來近似相關的概率分布，并能夠根據算法遞推更新離散隨機測度。當隨機樣本容量足夠大時，這種蒙特卡羅描述就近似于狀態變量真實的后驗概率密度函數。一般來說，粒子濾波的步驟主要包括3步：蒙特卡羅離散化、重要性采樣和序貫重要性采樣。

1.2.1 蒙特卡羅離散化

從后驗概率密度ρ(xk|z1∶k)中進行N次隨機采樣，得到N個粒子，后驗概率密度可近似表達為

(5)

式中δ(·)為沖激函數。遞推貝葉斯估計的核心問題是計算期望值，根據蒙特卡羅仿真離散化原理和大數定律，函數f(·)的數學期望可近似為

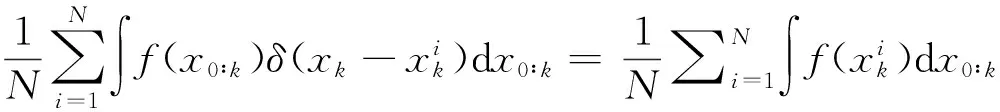
(6)

1.2.2 重要性采樣

(7)

1.2.3 序貫重要性采樣

為了能夠遞推估計概率密度，將建議分布分解為

q(x0∶k|z1∶k)=q(xk|x0∶k-1,z1∶k)q(x0∶k-1|z1∶k)，

(8)

綜上，粒子濾波算法步驟如下：

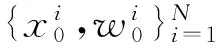
5)重采樣，得到新的粒子集合；

6)令k=k+1，轉到第2)步。

2 跟蹤算法描述

2.1 狀態模型

Xk=Xk-1+EK+Bυk，

(9)

2.2 觀測模型

綜上，可以得到基于粒子濾波的視頻目標跟蹤算法一般步驟，如圖1所示。

圖1 基于粒子濾波的視頻目標跟蹤算法流程圖

3 實驗結果與分析

本文實驗視頻幀率為15frame/s。實驗平臺為普通的PC,Pentium4 3GHzCPU,4G內存。算法使用Matlab實現。選擇其中幾幀演示跟蹤結果，如圖2所示。從實驗結果分析可知：本文算法始終能準確跟蹤到目標，達到良好的跟蹤效果，進一步驗證了該算法的有效性與穩健性。

第45幀

第100幀

第149幀

第201幀圖2 實驗結果示意圖

4 結語

本文探討了一種基于粒子濾波視頻目標跟蹤算法的應用。實驗結果表明，與傳統的目標跟蹤算法相比,本文提出的算法能實現對復雜情況下的非線性系統的目標的穩定準確跟蹤,將跟蹤精度提高到90%以上，具有較好的跟蹤效果。

[1] 朱志宇.流形粒子濾波算法及其在視頻目標跟蹤中的應用[M].北京:國防工業出版社,2015.

[2] 李靜,王軍政.圖像檢測與目標跟蹤技術[M].北京:北京理工大學出版社,2014.

[3] 王鑫,徐立中.圖像目標跟蹤技術[M].北京:人民郵電出版社,2012.

[4] 趙榮椿.數字圖像處理與分析[M].北京:清華大學出版社,2013.

[5]YilmazA,JavedO,ShahM.Objecttracking:asurvey[J].ACMComputingSurveys,2006,38(4):13-57.

[6]DoucetA,GodsillS,AndrieuC.OnsequentialmontecarlosamplingmethodsforBayesianfiltering[J].StatisticsandComputing,2000,10(3):197-208.

[7]CampilloF,RossiV.Convolutionparticlefilterforparameterestimationingeneralstate-spacemodels[J].IEEETransactionsonAerospaceandElectronicSystems，2009,45(3):1063-1072.

[8]SankalitaS,NealKB,ShuvraSB.Designandimplementationofembeddedcomputervisionsystemsbasedonparticlefilters[J].ComputerVisionandImageUnderstanding,2010,14(3):1203-1214.

The Application of Particle Filter Algorithm in Video Target Tracking

FU Hao-hai，et al.

(SchoolofComputerTechnologyandEngineering，ChangchunInstituteofTechnology，Changchun130012，China)

The paper first introduces the basic theory of particle filter，and then constructs a state model and observation model to particle filter in video target tracking system.According to the state model and observation model，it puts forward a video target tracking algorithm based on particle filter，and makes experimental analysis to this algorithm by the actual video target tracking system.It illustrates the advantages of particle filter algorithm in video target tracking.

bayesian filtering；particle filtering；video target tracking；algorithm application

10.3969/j.issn.1009-8984.2016.04.022

2016-09-16

長春工程學院青年基金(320150011)

付浩海(1982-)，男(漢)，山東臨沂，碩士 主要研究數字圖像處理和計算機視覺等。

TP391

A

1009-8984(2016)04-0085-04