基于帶數據約束實時系統的互模擬檢測方法

李國拯，高 正

(南京航空航天大學 計算機科學與技術學院，江蘇 南京 210016)

基于帶數據約束實時系統的互模擬檢測方法

李國拯，高 正

(南京航空航天大學 計算機科學與技術學院，江蘇 南京 210016)

帶數據約束的實時系統是指一種既帶有時間約束又帶有數據變量約束的計算系統，其廣泛存在于航空航天、工業控制、國防等安全攸關系統，并發揮著至關重要的作用。針對這類系統的形式化建模與驗證是確保其正確性和可靠性的重要途徑。文中首先研究了組合接口自動機、Z語言、時間自動機的形式規范—CT-ZIA，其能同時描述帶數據約束的實時系統的時序行為性質和數據結構性質；其次，為了研究該規范上的互模擬形式化驗證，給出了CT-ZIA上的互模擬關系定義；然后，為了互模擬算法的可判定性，對CT-ZIA中的時鐘進行等價劃分，提出了有限論域CT-ZIA的定義；最后，基于有限論域CT-ZIA模型，給出了其上互模擬檢測算法，并說明其正確性。

實時系統；接口自動機；Z語言；時間自動機；互模擬檢測

0 引 言

帶數據約束的實時系統[1]是指一種既帶有時間約束，又帶有數據變量約束的計算系統。飛行控制、核反應堆控制以及鐵路調度控制等計算機控制系統都屬于帶數據約束的實時系統。這些系統中許多動作的完成都與時間相關，即要滿足一定的時間限制，如某個動作要在一秒鐘內完成；同時這些系統中數據變量之間也有一定的約束關系，如飛機的飛行速度可能跟氣壓、溫度等有一定的約束關系。單一的規范技術很難適合這樣的應用場景，所以這就要求利用多種能夠描述系統行為各個方面的專門技術。基于這一想法，在文獻[2]中提出了組合接口自動機、時間自動機和Z語言的形式規范。

接口自動機(Interface Automata)[3]是一種輕量級的基于自動機語言的組件規范語言，能夠描述基于組件系統中組件及組件間的交互行為。時間自動機(Timed Automata)[4]是使用最為廣泛的一種描述實時系統的數學模型，可簡單看作帶時鐘變量的有限自動機。Z[5]是基于一階謂詞邏輯和集合論的形式規格語言。

文中研究了一種組合接口自動機、時間自動機和Z語言的規范語言，即CT-ZIA[2]。接口自動機是描述軟件組件接口性質的直觀模型，時間自動機是描述實時系統的模型，Z可以描述狀態的數據性質以及狀態的變遷。為了對復雜實時系統進行規范說明，這里簡單介紹下CT-ZIA的定義，粗略地講，CT-ZIA具有時間自動機風格和特點，但它的狀態和操作是用Z語言來描述的。文中進一步研究了CT-ZIA上的互模擬關系，并給出了有限論域CT-ZIA上的互模擬檢測算法。

1 連續時間ZIA規范

在文獻[2]中，提出了CT-ZIA規范，并研究其上的模型檢測[6]問題，下面直接給出其定義：

(1)SP是狀態的集合；

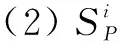
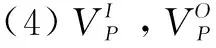
(7)X為時鐘變量的非負實數有限集合，C(X)為X上時鐘約束的集合，其語法定義如下：

Φ::=xc|cx|?1∧?2

其中，x∈X；∈{<,≤}；c為非負有理數。

(8)映射I：SP→C(X)為每個狀態賦以一時間約束，此約束稱為節點不變量；

2 CT-ZIAs間的互模擬關系

互模擬[7-8]是進程演算里的一個十分重要的概念，用來研究并發系統行為的一種方法。在軟件系統里，互模擬通常用來描述抽象規格說明與可執行程序代碼的相互轉換過程，所以互模擬關系的目的在于形式化說明相同組件的抽象和具體版本之間的關系，例如接口的規范與其實現之間的關系。

對于某個Z模式A，使用VI(A)代表A中的輸入變量集合，VO(A)代表A中的輸出變量集合，VH(A)表示A中的內部變量集合。

為了定義Z模式之間的互模擬關系，需要如下的符號。

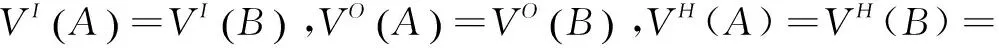
直觀上，A?B意味著模式A和模式B有相同的輸入變量和相同的輸出變量，并且模式A和模式B的輸入變量范圍和輸出變量范圍一樣。

現在給出Z模式之間的互模擬關系，其描述了狀態的數據結構屬性間的互模擬關系。粗略地講，對于模式A和模式B，說A和B是互模擬的，就是兩者的輸入輸出變量一樣，并且兩者的輸入變量范圍和輸出變量范圍也一樣。

定義3：考慮兩個Z模式A和B，使用符號A?B，如果

(1)VI(A)=VI(B)，VO(A)=VO(B)；

(2)A(x1,x2,…,xm)?B(y1,y2,…,yn)，其中{x1,x2,…,xm}=V(A)-VI(A)-VO(A)，{y1,y2,…,yn}=V(B)-VI(A)-VO(A)。

接下來給出CT-ZIAs間的互模擬關系。對CT-ZIAs來說，狀態不僅有數據屬性，還有行為屬性。因此，CT-ZIAs間的互模擬關系既包含數據屬性間的互模擬關系，又包含行為屬性間的互模擬關系。

定義4：給定一個CT-ZIAP，定義有序對(s,DP)∈SP×為P在某個時刻的狀態，其中是實數集合。下面定義P中的狀態變遷：

定義5：考慮CT-ZIAP和CT-ZIAQ，稱二元對稱關系R?(SP×)×(SQ×)是互模擬關系，需對(s,DP)∈SP×，(t,DQ)∈SQ×，(s,DP)R(t,DQ)推出如下條件滿足：

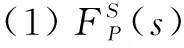
(2)對于時延d∈+，如果，那么存在時延d′∈+，使得以及；并且如果，那么存在時延d′∈+，使得以及；

3 有限論域CT-ZIA

考慮一個CT-ZIAP以及其上的狀態有序對(s,DP)∈SP×，顯然，P是一個無限狀態系統，為了互模擬算法的可判定性，需要首先將無限狀態轉為有限狀態。為了獲得CT-ZIA無限狀態空間的有限描述，下面給出有限論域CT-ZIA的定義。

Alur，Courcoubetis和Dill在文獻[9-10]中提出一種時鐘等價方法，把時間自動機等價為域自動機，但是按照Alur時鐘等價方法構造出的域自動機，存在狀態空間迅速膨脹爆炸的問題。在文獻[2]中，筆者采用一種優化的時鐘等價方法，并在此基礎上定義了適合于優化時鐘等價規則的域自動機，使等價后的域自動機狀態數盡量少[11]，這樣就將CT-ZIA等價為一種帶Z的域自動機。

大體思想如下：在構建時鐘等價規則時，主要考慮時鐘關鍵點的相互比較。例如，對狀態s來說，約束條件x≥2中的約束常量2是一個關鍵點，對于x的賦值v(x)來說，當v(x)>2或v(x)<2時，無論取何值都是不相關的，所以僅需要考慮約束常量這個關鍵點就可以了。

綜上所述，對時鐘x而言，可分為三種情況：

(1)v(x)

(2)v(x)=cx則v'(x)=cx；

(3)v(x)>cx則v'(x)>cx。

類似的，對于y-x的取值范圍，只需要考慮時鐘關鍵點的比較。

如上方法將CT-ZIA等價為一種帶Z的域自動機，下面對CT-ZIA中Z模式再加以適當的約束，就得到一類特殊的CT-ZIAs，其上的互模擬檢測算法是可判定的。

定義7:給定一個Z模式S[v1:T1;…;vm:Tm|P1;…;Pn]，如果模式中的每個變量vi有有限多可能的值，即變量的類型Ti有有限多元素，那么稱S為有限域Z模式。考慮一個，稱其為有限論域CT-ZIA，需滿足如下條件：

4 互模擬檢測算法

給定一個CT-ZIAP，可以將P轉為等價的帶Z域自動機，進一步約束P中Z模式的變量取值，就得到有限論域CT-ZIA，記為F(P)。這部分給出針對有限論域CT-ZIAs的互模擬檢測算法BC。假定F(P)和F(Q)是兩個有限論域CT-ZIAs，具體算法如下：

BC(P,Q)=

Rp,q:=BCS(p,q)

BCS(p,q)=

return(Bp,q)

elseB:=∧a∈A(p,q)Matcha(p,q)

Matcha∈A(p,q)(p,q)=

return(false)

return(false)

Di,j:=BCS(pi,qj)

return(∧i(∨j(Ca∧Ci,j∧Di,j)))

BCZ(S,T)=

if(VI(S)≠VI(T))or(VO(S)≠VO(T))

thenreturn(false)

else

VT:=V(T)-VI(S)-VO(S)

E:=BCL(SVS,TVT)

return(E)

BCL(M,N)=

TV(LS)=

rewriteschemaLStoanequivalentfirstorderlogicalformulaLF

if(LFisalwaystrueforanyassignmentonvariables)thenreturn(true)

elsereturn(false)

在上面的算法中，如果對任意賦值LS總是返回true，那么函數TV(LS)返回true。一般，因為一階邏輯的重言式問題是不可判定的，所以函數TV(LS)不能被實現，但是如果只考慮某些可判定的子邏輯，比如，邏輯公式的每個變量有有限多可能的值，這樣的子邏輯的重言式問題就是可判定的。因為LS是有限域Z模式，每個變量僅有有限多的可能的取值。

不難證明上文提出的互模擬檢測算法的正確性。下面給出上面算法的正確性說明：

引理1:算法BCZ(S,T)可以終止，并且是正確的，即算法返回true當且僅當S?T。

證明：由Z模式的精化關系定義可得引理1是正確的。

引理2:算法BCS(p,q)可以終止，并且是正確的，即算法返回true,當且僅當p～q。

證明：函數BCS(p,q)從有限劃分后的系統初始狀態有序對(p,q)出發，通過匹配從它們出發的變遷來檢測p,q之間的相似性。在遍歷變遷圖的過程中，算法根據CT-ZIA的變遷從每個狀態有序對產生接下來的變遷以及狀態，然后通過模擬來匹配變遷，如果匹配成功，算法就進入了下一對狀態有序對。函數Matcha在兩個變遷圖的乘積圖上執行深度優先的算法，如果一個狀態不能匹配另外一個狀態的變遷，那么它們間就不是互模擬關系，函數返回false，否則返回true。將P和Q進行了有限劃分得到有限狀態系統F(P)和F(Q)，這就保證了僅會有限次調用函數Matcha(p,q)，所以，函數BCS(P,Q)總是會終止。

通過上面的引理，即可得出下面的命題：

命題1:算法BCS(P,Q)可以終止，并且是正確的，即算法返回true當且僅當P～Q。

5 結束語

為了研究帶有數據約束的實時系統，文獻[2]中提出了組合接口自動機、時間自動機和Z語言三種形式規范說明技術的模型(CT-ZIA)，研究了其上的模型檢測問題，但是未對該模型進行進一步研究；文獻[12]提出了一種基于離散時間的ZIA規范，但是基于離散時間的模型較適用于同步系統；文獻[13]提出了混成ZIA模型，并給出了其上的近似精化關系定義，由于混成ZIA多數子集的不可判定性，未給出精化檢測算法。

文中給出了CT-ZIAs間互模擬關系的定義，并對CT-ZIAs中的時鐘進行等價劃分，給出有限論域CT-ZIA的定義，在其上的互模擬檢測算法是可以判定的，這對自動化驗證組件的規范與實現的關系有重大意義。

[1] 李廣元,唐稚松.帶有時鐘變量的線性時序邏輯與實時系統驗證[J].軟件學報,2002,13(1):33-41.

[2] 倪水妹,曹子寧,李心磊.帶數據約束實時系統的模型檢測[J].計算機科學,2014,41(5):254-262.

[3]deAlfaroL,HenzingerTA.Interfaceautomata[C]//ProcofACMSIGSOFTsoftwareengineeringnotes.[s.l.]:ACM,2001:109-120.

[4] Alur R,Dill D L.A theory of timed automata[J].Theoretical Computer Science,1994,126(2):183-235.

[5] Spivey J M.The Z notation:a reference manual[M].UK:Prentice Hall International Ltd,1992.

[6] 戎 玫,張廣泉.模型檢測新技術研究[J].計算機科學,2003,30(5):102-104.

[7] 朱維軍,劉保羅,周清雷.時間自動機與信號自動機的互模擬算法[J].華南理工大學學報：自然科學版,2008,36(5):38-42.

[8] 李 娜,姚從軍.互模擬的一些基本性質[J].云南師范大學學報：哲學社會科學版,2010,42(5):68-73.

[9] Alur R.Techniques for automatic verification of real-time systems[D].Stanford:Stanford University,1991.

[10] Alur R,Courcoubetis C,Dill D.Model-checking for real-time systems[C]//Proceedings of fifth annual IEEE symposium on logic in computer science.[s.l.]:IEEE,1990:414-425.

[11] 錢俊彥,趙嶺忠,古天龍.一種基于時間自動機的時鐘等價性優化方法[J].計算機工程,2005,31(18):71-73.

[12] 狄楊思.形式規范的自動驗證算法的研究[D].南京:南京航空航天大學，2012.

[13] Cao Z,Wang H.Hybrid ZIA and its approximated refinement relation[C]//Proceedings of the 6th international conference on evaluation of novel approaches to software engineering.Beijing,China:[s.n.],2011:260-265.

An Approach of Bisimulation Checking for Real-time System Based on Data Constraints

LI Guo-zheng，GAO Zheng

(School of Computer Science and Technology,Nanjing University of Aeronautics & Astronautics,Nanjing 210016,China)

Real-time systems with data constraints refer to computing systems both with time-bound and data variables constraints,which is widely used in safety-critical areas like aerospace,industry control,defense system,playing an important role.Formal modeling and verification for these systems is an important way to ensure the correctness and reliability of the systems.In this paper,study a specification model combining interface automata,timed automata and Z language,named CT-ZIA.This model can be used to describe temporal properties and data properties of real-time systems with data constraints.Second,in order to study formal verification for bisimulation in the specification,the bisimulation definition for CT-ZIA is given.Then,for the decidability of simulation algorithm,each clock of CT-ZIA is partitioning in equivalence,putting forward the definition of limited domain CT-ZIA’s.Finally,give an algorithm for checking bisimulation relation between CT-ZIAs with finite domain and demonstrate the correctness of the algorithm.

real-time system;interface automata;Z notation;timed automata;bisimulation checking

2014-11-25

2015-03-04

時間：2016-01-04

航空科學基金(20128052064)；中央高校基本科研業務費專項資金(NZ2013306)；國家“973”重點基礎研究發展計劃項目(2014CB744903)

李國拯(1990-)，男，碩士研究生，研究方向為形式化方法、模型檢測。

http://www.cnki.net/kcms/detail/61.1450.TP.20160104.1608.084.html

TP311

A

1673-629X(2016)01-0006-04

10.3969/j.issn.1673-629X.2016.01.002