最大流問題的改進最短增廣鏈算法
ZHAO Li-feng,JI Ya-bao
(College of Science,Nanjing University of Posts and Telecommunications,Nanjing 210023,China)
最大流問題的改進最短增廣鏈算法
在最大流問題中,由于Ford-Fulkerson算法中增廣鏈選取的任意性,導致該算法不是有效的多項式算法。經典的最短增廣鏈算法是通過在增廣過程中尋找最短增廣鏈,從而排除增廣鏈選取的任意性。但計算過程中為尋找最短增廣鏈,需要根據原網絡循環地構建剩余網絡和剩余分層網絡,步驟非常繁雜。為改善以上不足,基于經典最短增廣鏈算法,提出改進最短增廣鏈算法。該算法的思想是:若在增廣剩余分層網絡中流值的過程中得到飽和弧,則刪除該弧對應于原網絡中的弧,使原網絡得以簡化,以此可降低構建剩余網絡和剩余分層網絡的復雜性,從而優化最短增廣鏈算法。理論和仿真實驗都表明,改進算法不僅正確,而且比原算法效率更高。
最大流;最短增廣鏈;剩余網絡;剩余分層網絡
0 引 言
網絡最大流問題是經典的組合優化問題,是網絡流理論中的重要組成部分。最大流問題在現實生活中以及眾多科學領域中都有著廣泛的應用,例如常見的交通網絡以及通信網絡都可以轉化成最大流問題來解決。因此網絡流的研究具有重要的現實意義,它可以優化結構、提高效率、發揮最大的社會和經濟效益。
對網絡最大流理論的研究已經取得了大量成果,并且也形成了完善的理論體系。最大流問題的經典算法可以分為增載軌類算法和預留推進類算法[1]。在增載軌類算法中有1956年發現的Ford-Fulkerson算法[2]和Dinic等提出的改進Ford-Fulkerson算法(每次都沿著最短增廣鏈增廣)。Edmonds和Karp[3]提出利用剩余網絡尋找最短增廣鏈的最短增廣鏈算法。Dinic[4]構建了阻塞流和分層網以設計最短增廣鏈算法。預留推進類算法中包括由Goldberg和Tarjan提出的預流推進算法[5]。在這些研究之后又有一些針對特殊網絡而提出的最大流問題的算法[6-12],包括對于稀疏網絡、小容量網絡、無向網絡、點邊有容量約束網絡、節點環流型網絡、單位容量網絡等,文獻[13-14]對經典的最大流算法進行了研究。
對于Dinic等基于最短增廣鏈提出的最短增廣鏈算法,需要循環構建剩余網絡和分層網絡,這個過程往往比較復雜。
文中在增廣過程中刪除某些已經不再增廣的弧,從而簡化了原網絡,減少了構建剩余網絡和分層網絡的復雜性,優化了最短增廣鏈算法。
1 相關知識
1.1 最大流問題線性規劃模型
模型如下:
1.2 剩余網絡
給定一個帶發點vs和收點vt的容量網絡N=(V,vs,vt,E,C)及N上的可行流f,定義
A(f)=A+(f)∪A-(f)
稱cij(f)為弧(vi,vj)關于f的剩余容量。于是得到一個帶發點vs和收點vt的容量網絡N(f)=(V,vs,vt,A(f),cf),稱之為N關于f的剩余網絡。
1.3 剩余分層網絡
對于N的關于f的剩余網絡N(f)=(V,vs,vt,A(f),cf),定義N(f)的子網絡EN(f)=(V'(f),A'(f),cf)如下:
V'(f)={vt}∪{vi∈V|h(vi) A'(f)={(vi,vj)∈A(f)|h(vj)=h(vi)+1 EN(f)稱為N關于f的剩余分層網絡。 2.1 最短增廣鏈算法步驟 在網絡N=(V,vs,vt,E,C)中,從任意一個可行流f(一般可取零流)開始,執行以下步驟: 步驟1:構造剩余網絡N(f)并對其分層,構造剩余分層網絡EN(f)。若EN(f)中y得不到標號,結束,f就是最大流,否則轉步驟2。 步驟2:求EN(f)中vs→vt的一條路p,并沿路p增加流得到更大的流,并去掉EN(f)中所有飽和弧。 步驟3:求EN(f)中vs→vt的一條路p,若不存在則返回步驟1;否則返回步驟2。 2.2 改進算法思想 在最短增廣鏈算法步驟3中,當EN(f)中不存在vs→vt路時,就返回步驟1,在步驟1中重新構造剩余分層網絡。在這個過程中發現,對于步驟2中增廣流后而得到的飽和弧在步驟1中的剩余分層網絡并不存在,即最短增廣鏈算法步驟2中增廣流后而得到的飽和弧在以后的增廣過程中這條弧的流值不可能增加或減少。 于是,在改進算法中,只需要刪去原網絡中的這些飽和弧,便可以簡化步驟1中重新構造網絡的過程。 2.3 改進算法正確性和時間復雜度 定理1:對于最短增廣鏈上增廣流值后而得到的飽和弧,在以后的算法進程中這條弧上的流值不可能再增加或減少。 證明:對這些飽和弧首先要構造剩余網絡,再對其進行分層,最后構造出剩余分層網絡。在剩余分層網絡中尋找vs→vt路,對vs→vt路進行圖中各個頂點的層次只可能增加或不變而不可能減少。已知在剩余分層網絡中尋找的vs→vt路對應于原網絡的增廣鏈,現假設vs→vt路中的某條弧e對應于原網絡增廣鏈中的前向弧,則實際情況是對弧e增加流值,當增加流值未達到飽和時則在剩余分層網絡中與弧e關聯的節點的層次沒有改變,若增加流值達到飽和時與在剩余分層網絡中與弧e關聯的節點層次就會增加。再假設vs→vt路中對應于原網絡中的后向弧,則實際情況是對弧e減少流值,當減少流值未達到飽和時則在剩余分層網絡中與弧e關聯的節點的層次沒有改變,若減少流值達到飽和時與在剩余分層網絡中與弧e關聯的節點層次就會增加。于是增流達到飽和的弧在重新構造剩余分層網絡時不滿足頂點層次要求,故不存在于重新構造的剩余分層網絡中。即這條弧不可能存在于以后的增廣過程中。 定理2:改進算法時間復雜度為O(n2m)。 證明:設容量網絡D的頂點數為n,弧數為m。步驟1中最多執行n-1次,又由廣探法知,每次構造剩余分層網絡的復雜性為O(m)。步驟2和步驟3中最多增廣m次,而每次增廣的計算量為O(n),所以改進的最短增廣鏈算法的算法復雜度為O(nm)+O(n2m)=O(n2m)。 2.4 改進算法步驟 步驟1:構造剩余網絡N(f)并對其分層,構造剩余分層網絡EN(f)。若EN(f)中y得不到標號,結束,f就是最大流,否則轉步驟2。 步驟2:求EN(f)中vs→vt的一條路p,并沿路p增加流得到更大的流,并去掉EN(f)中所有飽和弧。 步驟3:求EN(f)中vs→vt的一條路p,若不存在,則將在步驟2中達到飽和的弧在原網絡中刪除,再返回步驟1;否則返回步驟2。 例:求圖1中網絡最大流。 圖1 原網絡圖 圖中,弧上的數字表示弧容量,初始流為零流。首先通過剩余分層網絡,最短增廣鏈為3條弧。通過步驟1~3得到增廣流值如圖2所示。流值為7,在增廣流值的過程中弧(v2,v3)和弧(v1,v4)達到飽和,增廣流值后EN(f)中不存在x→y的一條路p,即原網絡中不存在只有3條弧的增廣鏈。 圖2 增廣流值后的網絡圖 于是返回步驟1,在原網絡中刪除弧(v2,v3)和(v1,v2),再構建剩余分層網絡,見圖3。接著進行步驟2和步驟3,此時最短增廣鏈v1→v2→v4→v5→v6含有4條弧。 圖3 刪除飽和弧(v2,v3)、(v1,v2) 增廣流值后流值為8。在增廣過程中弧(v4,v5)達到飽和,增廣流值后EN(f)中不存在x→y的一條路p,即原網絡中不存在只有4條弧的增廣鏈。再返回步驟1在原網絡中刪除弧(v2,v3)、(v1,v4)和(v4,v5),再構建剩余分層網絡,見圖4,此時剩余分層網絡中v6得不到標號。于是圖4即為最大流,流值為8。 圖4 刪除飽和弧(v1,v4)后的剩余分層網絡圖 文中MATLAB仿真實驗是在網絡規模為500,1 500,2 500和3 500個節點的隨機網絡上對經典算法和改進算法的運行時間進行比較(見表1),針對每個規模的網絡均進行十次實驗求平均值。隨機網絡是由經典BA無標度網絡的方法隨機生成。 表1 兩種算法所得到的最大流值 通過表1可以看出,兩種算法同樣都能求解出最大流,并且都能求出網絡中每條弧中的具體流值(由于網絡比較大,具體流值情況沒有寫入)。 圖5的實驗結果表明,改進算法相對于原算法節省了運行時間,這與之前的分析吻合,并且節點數越多,改進算法效率越高。 圖5 算法運行時間對比 在網絡最大流問題中最短鏈增廣鏈算法是經典算法。該算法是對2F算法的改進,是一種強多項式算法,算法效率高。該算法對2F算法進行的改進是為了避免增廣鏈選取的任意性,每次增廣都通過構建剩余網絡和分層網絡來尋找最短增廣鏈,從而使得算法的復雜性不再取決于網絡容量,而僅僅取決于網絡節點數和邊數。但是構建剩余網絡和分層網絡均比較復雜。文中在算法循環進行的過程中不斷簡化需要構建的剩余網絡和層次網絡,從而減少了構建剩余網絡和分層網絡的復雜性。 [1] 張憲超,陳國良,萬穎瑜.網絡最大流問題研究進展[J].計算機研究與發展,2003,40(9):1281-1292. [2]FordLR,FulkersonDR.Maximumflowthroughanetwork[J].CanadianJournalofMath,1956,8(5):399-404. [3]EdmondsJ,KarpRM.Theoreticalimprovementsinalgorithmicefficiencyfornetworkflowproblems[J].JournaloftheAssociationforComputingMachinery,1972,19(2):248-264. [4]DinicEA.Algorithmsforsolutionofaproblemofmaximumflowinnetworkswithpowerestimation[J].SovietMathematicsDoklady,1970,11(8):1277-1280. [5] 謝 政.網絡算法與復雜性理論[M].長沙:國防科技大學出版社,2003. [6] 趙禮峰,嚴子恒.基于增廣鏈修復的最大流求解算法[J].計算機應用,2015,35(5):1246-1249. [7] 張憲超,陳國良.小容量網絡上的最大流算法[J].計算機研究與發展,2001,38(2):194-198. [8] 邱偉星,王以凡,沈金龍.一個求無向網絡最大流的算法[J].南京郵電學院學報,1997,14(4):170-172. [9] 郭 強.無向網絡最大流問題研究[J].計算機工程與應用,2005,41(9):76-78. [10] 張憲超,江 賀,陳國良.節點和邊都有容量的有向平面網絡中的最小截和最大流[J].計算機學報,2006,29(4):544-551. [11] 徐光聯,孫文新.節點環流網絡中的最大流算法[J].應用科技,2014,41(1):48-53. [12] 張憲超,江 賀,劉馨月,等.無向平面單位容量網絡中的最大流[J].計算機研究與發展,2008,45(S1):40-42. [13] 孫澤宇,丁國強,程志謙.網絡最大流求解算法的研究[J].微計算機信息,2010,26(1-3):143-145. [14] 孫澤宇.基于標號法求解網絡最大流算法的研究[J].甘肅聯合大學學報:自然科學版,2009,23(4):64-66. 趙禮峰,紀亞寶 (南京郵電大學 理學院,江蘇 南京 210023) Improved Shortest Augmenting Chain Algorithm of Maximum Flow In maximum flow problem,since the Ford-Fulkerson algorithm chooses arbitrarily augmented chain,as a result the algorithm is not a valid polynomial one.Classical shortest augmenting chain algorithm is to find the shortest augmenting chain in the augmented chain process,thus eliminating the arbitrary of augmented chain selection.But in calculation process for finding the shortest augmenting chain,needing to build the remaining network and the remaining surplus hierarchical network based on the original network cycle,its step is very complicated.In order to improve the above problems,based on the classical shortest augmenting chain algorithm,an improved one for the shortest augmenting chain is put forward.The idea is that if the saturated arc is obtained in flow value processing augmented remaining hierarchical network,then the original arc corresponding to the network is deleted,making the original network simplified in order to reduce the complexity of constructing remaining network and the remaining layered network and optimize the shortest augmenting chain algorithm.The theory and simulation show that the improved algorithm is not only correct,but also higher in efficiency than the original algorithm. maximum flow;shortest augmenting chain;remaining network;remaining layered network 2015-12-02 2016-03-09 時間:2016-08-01 國家自然科學基金青年基金項目(61304169) 趙禮峰(1959-),男,教授,碩士研究生導師,研究方向為圖論及其在通信中的應用;紀亞寶(1990-),男,碩士研究生,研究方向為圖論及其在通信中的應用。 http://www.cnki.net/kcms/detail/61.1450.TP.20160801.0907.044.html TP301.6 A 1673-629X(2016)08-0052-03 10.3969/j.issn.1673-629X.2016.08.011 ZHAO Li-feng,JI Ya-bao (College of Science,Nanjing University of Posts and Telecommunications,Nanjing 210023,China)2 改進的最短增廣鏈算法
3 數值實例

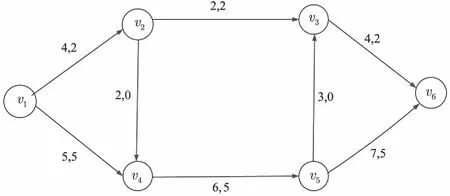


4 算法的仿真與比較

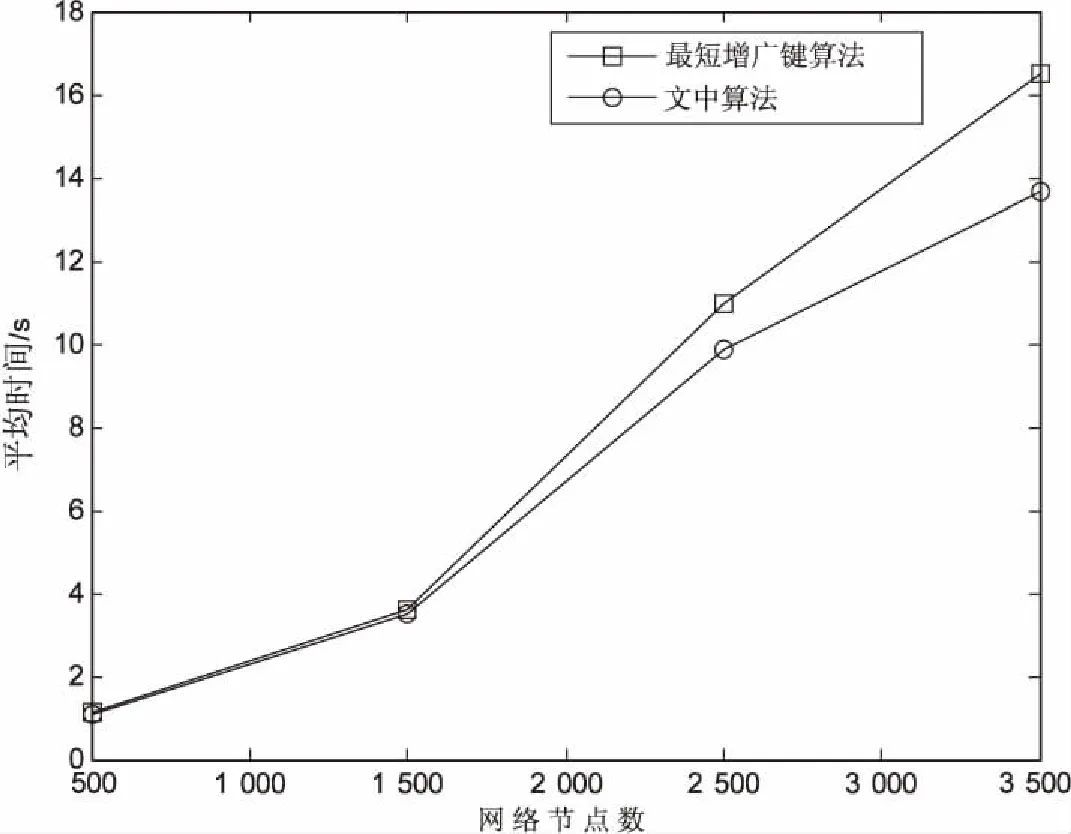
5 結束語

