自適應CPSO算法在云計算任務調度中的應用

張曉麗

(西安航空學院 計算機學院,陜西 西安 710077)

自適應CPSO算法在云計算任務調度中的應用

張曉麗

(西安航空學院 計算機學院,陜西 西安 710077)

云計算環境中的任務調度問題一直是云計算研究的重點。為了克服傳統PSO算法易陷入局部最優的缺陷，針對云計算的編程模型框架，將混沌優化搜索技術應用于粒子群優化算法，提出一種基于Tent映射的自適應混沌粒子群任務調度算法。該算法結合了PSO算法的快速收斂性和混沌運動的遍歷性、隨機性，在初始化粒子的位置時采用混沌賦值的方式產生一系列初始解，再根據每個粒子個體的適應值來自適應地調整其慣性權重，對陷入局部最優的粒子群個體位置進行混沌更新，幫助其跳出局部最優。通過在CloudSim平臺進行仿真對比實驗，表明該改進算法有效地縮小了總任務的完成時間，具有較好的尋優能力和實時性，是一種有效的云計算任務調度算法。

云計算；任務調度；粒子群優化算法；混沌

0 引 言

云計算[1-2]作為一種新型的計算服務商業模式，集成了網格計算、分布式計算和并行計算等技術，自提出以來就成為一個熱點研究方向。云計算提供了基礎設施、平臺和軟件的服務，可以將用戶提交的任務按照適當的算法分配到虛擬計算資源上進行合理調度，之后再將服務器的計算分析處理結果發送給用戶。

由于云計算中存在諸多形態不同的云端，且面對的計算資源種類眾多、提供服務效率不一、計算任務數量巨大，因此在“云”中如何將眾多任務進行合理調度以滿足用戶對服務質量的要求，并且更有效利用云計算系統中的資源，一直是一個熱點問題[2-3]。云計算任務調度是云計算研究的重點，它主要解決的問題是如何以最優的調度策略實現用戶任務的有效調度。云計算任務調度問題實際上是一個NP難題[4]。針對該問題，國內外學者對其進行了大量的研究，提出了眾多云計算任務調度算法。如最小最小(Min-Min)[5]、Sufferage算法[6]、蟻群算法[7]、遺傳算法[8]、粒子群優化算法[9]等。

PSO算法[10]是一種基于群體的智能優化算法，從隨機解出發，通過迭代尋找最優解。相比較于遺傳算法或蟻群算法等全局優化算法，PSO算法具有設置參數少、易實現、精度高、收斂快等優點，在求解云計算任務調度問題上具有天然的優勢。但是同其他一些智能優化算法一樣，PSO算法也存在著容易出現早熟收斂、陷入局部最優等缺點。

為了克服傳統PSO算法易陷入局部最優解的缺陷，文中通過對如何充分利用“云”中的資源使其中的任務進行高效合理的調度進行了研究，利用云模型的隨機性和穩定性的特點，在傳統PSO優化算法的基礎上提出了一種基于云模型的自適應CPSO任務調度算法，采用混沌變量來優化粒子的位置和速度，并對每次混沌搜索的范圍采用自適應調整方法，從當前群體中擇優選擇部分粒子進行混沌優化。

1 云計算中的任務調度模型

目前，大部分云計算平臺都采用Google提出的Map/Reduce分布式計算編程模型[11]。這是一種用于大規模數據集的并行編程架構，分為Map和Reduce兩個階段，實現將一個較大的任務切分為多個較小的子任務，交給n臺計算機并行執行，再并行遞歸并返回結果，最后得到運算結果。

云計算環境下的任務調度是以任務為出發點，根據一定的任務調度策略，將相互獨立的多個任務以最合理的方案分配到可用的計算資源上，使得任務的總執行時間跨度最短同時能夠充分利用現有資源。因此云計算任務調度算法的優劣直接影響任務的執行效率，從而影響整個云的性能和用戶的滿意度。根據云計算任務調度的特點，定義如下的數學參數模型：G=(T,R,F,P)。

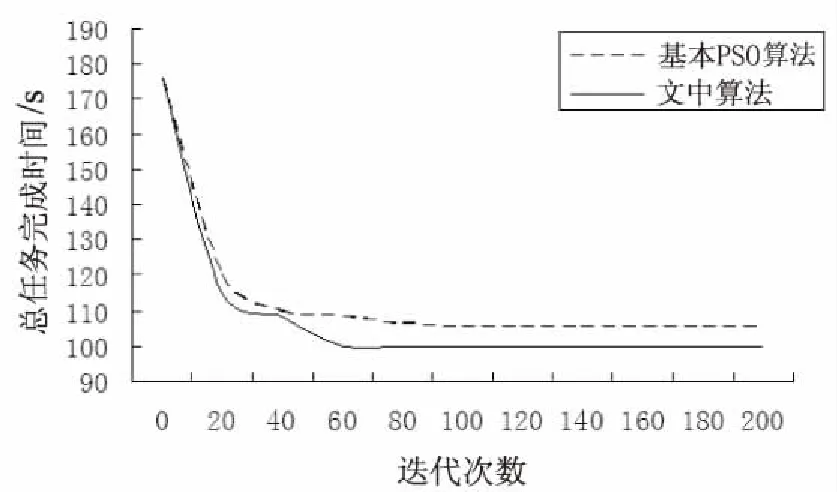
其中，T={T1,T2,…,Tn}表示任務模型，包括n個相互獨立的任務；R={R1,R2,…,Rm}表示由m個可用于執行任務的高性能計算資源組成的計算資源模型，其中m

定義了以上的任務調度模型，使用n×m的ETC矩陣來描述各個計算資源上任務隊列運行完成所需要的時間。其中，ETC(i,j)表示第j個計算資源上執行第i個子任務所需要的時間。

假設第j個資源上分配的的子任務的個數為M，那么資源j上的所有子任務執行完成所需要的時間應該為：

(1)

可以得到完成所有任務的總時間為：

(2)

則任務的平均完成時間為：

Tavg=SumTime/n

(3)

2 標準粒子群算法

粒子群優化算法[10]是Kennedy和Eberhart在1995年受飛鳥集群活動的規律性啟發提出的一種全局優化進化算法。該算法通過目標函數適應度的值來分配相關資源。由于該算法簡單易實現且沒有太多參數需要調整，因而在求解云計算任務調度這個大規模、實時問題時能得到較好的效果。

PSO同遺傳算法類似，是一種基于迭代的優化算法。傳統PSO算法中，每一個粒子代表一個可行解，且每一個粒子均有一個初始位置和速度，粒子的優劣程度取決于待優化問題目標函數確定的適應度值。系統初始化為一組隨機解，通過迭代在解空間追隨最優的粒子進行搜索，從而找到最優值。在每一次迭代中，粒子通過跟蹤兩個“極值”來更新自己，其中一個就是粒子本身所找到的最優解，即個體極值pbest，另一個則是整個種群目前找到的最優解，即全局極值gbest。在找到這兩個最優值時，粒子根據式(4)和式(5)來更新自己的速度和位置：

v(t+1)=wv(t)+c1r1(pbest(t)-x(t))+ c2r2(gbest(t)-x(t))

(4)

x(t+1)=x(t)+v(t+1)

(5)

其中，v為粒子的速度；x為粒子的位置；c1和c2為加速因子；r1和r2為[0,1]的隨機數；w為慣性權重。

3 自適應CPSO算法

3.1 CPSO算法

混沌是存在于非線性系統中的一種無規則的運動現象，混沌優化算法的基本思想是把混沌變量從混沌空間映射到解空間。由于混沌變量具有遍歷性、隨機性和規律性，利用混沌變量進行優化搜索能加速算法搜索速度、避免算法陷入局部最優，從而提高算法的搜索性能。

標準PSO算法是一種簡潔高效的智能優化算法，但是由于算法隨機性很大，仍有很多不完善的地方，例如容易出現收斂過早、陷入局部最優等問題。為彌補該缺陷，文中將混沌思想引入粒子群優化算法，提出一種混沌粒子群優化算法。

在算法初始化時利用混沌賦值的方式對粒子群進行初始化，同時在算法搜索過程中將混沌范圍擴大到優化變量的取值范圍中，充分利用PSO算法收斂速度快以及混沌運動遍歷性、隨機性和規律性的優點，對種群中處于最差位置的粒子個體進行混沌優化,從而提高傳統粒子群算法的收斂速度和尋優效率。不同的混沌映射方程對混沌尋優過程有很大的影響。文獻[12]通過比較指出，相比Logistic映射，Tent映射具有更快的迭代速度和更高的遍歷均勻性，因此文中采用Tent映射作為混沌優化模型，其表達式為:

(6)

文中提出的基于Tent映射的混沌粒子群(CPSO)算法的基本思想是：當PSO算法出現早熟收斂時,引入混沌Tent映射,對全局最優粒子進行混沌搜索，通過改變粒子個體位置的更新策略來引導粒子群進行一定次數的混沌更新,使其快速跳出局部最優。當算法出現早熟收斂時，使用式(7)對位置變量進行更新：

x(t+1)=xmin+zk+1×(xmax-xmin)

(7)

3.2 自適應慣性權重

PSO算法的性能優劣與參數慣性權重w的取值有著密切的關系。w取值越小越有利于局部搜索，并且能得到較為精確的解，但搜索時不易跳出局部極值點；相反，w取值越大越有利于全局搜索，但不易得到精確的解。對此，為了加強算法在全局和局部搜索之間的平衡，文中結合CPSO優化算法，提出一種基于粒子個體適應值的自適應慣性權重：

(8)

其中，wmax為慣性權重的最大值；wmin為慣性權重的最小值；t為當前的迭代次數；G為最大迭代次數。

可見，通過式(8)來計算每個粒子的慣性權重系數，對每次混沌搜索的范圍采用自適應調整方法。在算法初期w取較大的值，使算法具有較強的全局搜索能力；而算法后期w使用較小的值，從而提高算法的局部搜索能力。

3.3 適應度函數的選取

在PSO算法中，適應度函數的選取是相當重要的。適應度函數直接影響算法的收斂速度與最優解的查找，適應度值越大，表示相對應粒子質量越好。云計算任務調度目標是總任務完成時間最短，文中根據任務總完成時間來定義適應度函數：

(9)

文中采用類似遺傳算法的選擇思想，優先選擇適應度高的粒子。由式(9)可知，任務總完成時間越小的粒子，適應度值越大，則越容易被選擇。

3.4 算法流程

文中將混沌優化思想用于粒子群優化算法，并結合動態慣性權值因子，提出一種自適應的混沌粒子群優化算法。以粒子變量為基礎，在初始化粒子群中粒子的位置時采用混沌賦值的方式，對粒子產生混沌擾動形成混沌序列，以此替換原有粒子，提高粒子性能。算法在初始化粒子位置時采用混沌賦值的方式產生一系列初始解，從中擇優選出初始群體，提高粒子群的多樣性和粒子搜索的遍歷性。其次在粒子群優化過程中，根據每個粒子個體的適應值來自適應地調整其慣性權重，對粒子群個體位置進行混沌更新，幫助其跳出局部極值區間，提高了算法的收斂速度和精度。

具體實現步驟如下：

(1)采用混沌理論產生初始群體。利用混沌優化的隨機性、遍歷性特點對粒子群算法進行混沌初始化，從中擇優選擇粒子作為初始粒子，在保證隨機性的前提下使初始粒子盡可能分布均勻。

(2)混沌初始化各粒子的位置和速度，根據式(9)計算粒子群的適應度值。

(3)根據式(8)自適應地調整粒子的慣性權重。

(4)對于每個粒子的適應度值與原來的個體極值pbest和全局極值gbest進行比較，如果粒子的適應度值優于pbest，那么將其作為當前的個體極值；如果粒子的適應度值優于gbest，則將其作為當前的全局極值點。

(5)對每個粒子，按式(4)更新速度,按式(5)和式(7)更新位置。

(8)判斷是否滿足停止條件，如果滿足則停止搜索，輸出全局最優位置，否則返回步驟(4)。

4 實驗結果及分析

為了檢測文中算法的有效性，采用墨爾本大學開發的云仿真平臺CloudSim[13]來模擬一個云計算的局部環境，在相同實驗條件下，對傳統PSO算法和文中算法進行了云計算環境下的仿真對比實驗，分別從收斂性和任務完成時間兩個方面對算法性能進行對比。

(1)算法的收斂性對比。

在云計算資源數為10,調度任務數為100的環境下,基本參數設置一致，對文中算法和基本PSO算法調度方案的收斂性進行仿真實驗，收斂曲線如圖1所示。

由圖1可知,相較于基本PSO算法而言，文中方法的收斂速度明顯占據優勢，并且比基本PSO算法優先達到最優方案。這是因為在迭代過程中，由于文中方法引入混沌機制對基本的粒子群進行混沌擾動，避免粒子陷入局部最優，并且在迭代中采用了動態自適應的慣性權重機制，提高了算法的尋優能力。

圖1 算法改進前后的收斂曲線圖

(2)總任務完成時間對比。

考慮到云環境任務具有動態性的特點，分別模擬10個計算資源、50個子任務以及10個計算資源、500個子任務兩種實驗環境，對基本PSO算法和文中算法的性能進行了對比實驗。兩種算法分別運行100次，取100次實驗的平均結果作為實驗的最終結果。根據文獻[14]的參數調整原則，設置兩種算法的基本參數，如表1和表2所示。

表1 文中算法主要參數設置

表2 PSO算法主要參數設置

在參數設置基本一樣的情況下，分別進行200次迭代，兩種調度算法的對比結果如圖2和圖3所示。

圖2 任務較少時，兩種算法總任務完成時間比較

從圖2和圖3可以看出，基本PSO算法和文中算法在迭代初期任務的總完成時間相差不大，隨著迭代次數的增大，兩種算法的任務總完成時間都在不斷減小。相比而言，由于基本PSO算法只重視總任務的完成時間，在迭代初期收斂速度快，但在運行過程中由于無法有效跳出局部最優而出現了早熟收斂，過早地收斂到局部最優的任務調度結果。因此采用基本PSO算法的調度優化效果，迭代初期比較明顯，但是隨著迭代次數的增加，探索能力不足，在進化前期迅速地探索到局部最優解后就沒能再跳出。而文中算法將混沌機制引入基本PSO算法，在迭代過程中不斷優化調度結果。對比圖2和圖3可以看出，當任務數增加到100時，使用文中算法得到的總任務完成時間明顯優于使用基本PSO算法調度的總任務完成時間，且收斂速度也優于傳統的PSO調度算法。

圖3 任務較多時，兩種算法總任務完成時間比較

(3)任務平均完成時間對比。

為了更好地驗證和評價文中算法的性能，將其與改進遺傳算法(GA)[7]、改進蟻群算法(ACO)[15]進行對比試驗。設置計算資源節點數為10，待調度的子任務數為100，在相同的實驗環境下，分別測試三種算法迭代100次后得到的任務平均完成時間，對比結果如圖4所示。

圖4 任務平均完成時間比較

從圖中可以看出，文中的CPSO算法結合了PSO算法的快速收斂能力以及混沌優化算法的遍歷性和隨機性特點，能夠有效降低算法陷入局部極小的概率，在迭代過程體現了均衡的探索能力和開發能力，在三種調度算法中表現最優。ACO算法在整個迭代過程中，迭代初期優化效果比較明顯，但是在迭代后期優化效果變弱，任務平均完成時間大于遺傳算法和文中算法，調度效果相對較差。GA算法在整個迭代過程中優化能力比較均衡，但是收斂速度相對較慢。因此，無論是任務的平均完成時間還是算法的收斂速度，文中提出的CPSO算法都優于ACO算法和GA算法。

5 結束語

針對當前云計算任務調度算法存在收斂速度慢、資源利用率不足等缺陷，利用PSO算法控制參數少、易于實現、計算簡單等優點，文中提出一種云計算環境下基于混沌粒子群優化的任務調度算法。在PSO算法中引入混沌搜索，采用混沌賦值的方式初始化種群，并使用自適應的慣性權值控制粒子的搜索范圍，使粒子自適應地進行搜索。通過對比實驗可知，文中提出的基于Tent映射的自適應CPSO算法很好地解決了標準PSO算法容易“早熟”的問題，提高了任務和資源之間的匹配度，并且有效縮短了總任務的完成時間，具有較好的尋優能力，能夠有效地解決云計算環境下的任務調度問題。

[1]FosterI,ZhaoYong,RaicuI,etal.Cloudcomputingandgridcomputing360-degreecompared[C]//Procofgridcomputingenvironmentsworkshop.WashingtonD.C.,USA:IEEEComputerSociety,2008:1-10.

[2]ArmbrustM,FoxA,GriffithR,etal.Abovetheclouds:aberkeleyviewofcloudcomputing[EB/OL].2009-11-21.http://www.eecs.berkeley.edu/Pubs/TechRpts/2009/EECS-2009-28.pdf.

[3] 鄒永貴，萬建斌．云計算環境下的資源管理研究[J]．數字通信，2012(4):39-43．

[4]ArfeenMA，PawlikowskiK，WilligA．Aframeworkforresourceallocationstrategiesincloudcomputingenvironment[C]//ProcofIEEE35thannualcomputersoftwareandapplicationsconferenceworkshops.[s.l.]:IEEE,2011:261-266．

[5] 羅 紅，慕德俊，鄧智群，等.網格計算中任務調度研究綜述[J].計算機應用研究,2005,22(5):16-19.

[6]BuyyaR.Economic-baseddistributedresourcemanagementandschedulingforgridcomputing[D].Melbourne,Australia:MonashUniversity,2002.

[7] 王 芳，李美安,段衛軍.基于動態自適應蟻群算法的云計算任務調度[J].計算機應用，2013，33(11):3160-3162.

[8] 林劍檸,吳慧中.基于遺傳算法的網格資源調度算法[J].計算機研究與發展，2004，41(12):2195-2199.

[9] 季一木，王汝傳.基于粒子群的網格任務調度算法研究[J].通信學報，2007，28(10)：60-66.

[10]KennedyJ,EberhartR.Particleswarmoptimization[C]//ProcofIEEEinternationalconferenceonneuralnetworks.Piscataway,NJ:IEEE,1995:1942-1948.

[11]DeanJ,GhemawatS.MapReduce:simplifieddataprocessingonlargeclusters[C]//Proceedingsofthe6thsymposiumonoperatingsystemdesignandimplementation.NewYork:ACM,2004:137-150.

[12] 單 梁，強 浩，李 軍,等．基于Tent映射的混沌優化算法[J]．控制與決策，2005，20(2):179-182．

[13]CalheirosRN,RanjanR,BeloglazovA,etal.CloudSim:atoolkitformodelingandsimulationofcloudcomputingenvironmentsandevaluationofresourceprovisioningalgorithms[J].Software:PracticeandExperience,2011,41(1):23-50.

[14] 段海濱,張祥銀,徐春芳.仿生智能計算[M].北京：科學出版社,2011:63-85.

[15] 李建鋒,彭 艦.云計算環境下基于改進遺傳算法的任務調度算法[J].計算機應用，2011，31(1):184-186.

Application of Self-adaptive Chaos Particle Swarm Optimization in Task Scheduling for Cloud Computing

ZHANG Xiao-li

(School of Computer,Xi’an Aerotechnical University,Xi’an 710077,China)

Tasks scheduling is an important issue to be resolved in cloud computing research.In order to overcome the defects of traditional PSO easy to fall into local optimum,in view of procedure model framework of cloud computing,the chaos optimization search technique is applied to the particle swarm optimization，and an adaptive chaotic particle swarm algorithm of task scheduling based on Tent mapping is presented.It combines the fast convergence of PSO and the ergodic property of chaotic motion,with chaotic assignment way in initializing particle position,and then adaptively adjusts its inertia weight according to the fitness value of each individual particle,updating chaos location for particle swarm individual to help themselves escape from local optima.Through simulation experiment on the CloudSim platform,the results show that the ACPOS,with a good real-time performance and optimization ability,significantly reduces the completion time of the task,which is an efficient task scheduling algorithm.

cloud computing;task scheduling;Particle Swarm Optimization (PSO);chaos

2015-10-28

2016-01-28

時間：2016-06-22

西安市科技計劃項目資助(CXY1518(1))

張曉麗(1980-),女,講師，碩士,研究方向為云計算、分布式計算。

http://www.cnki.net/kcms/detail/61.1450.TP.20160622.0844.032.html

TP393

A

1673-629X(2016)08-0161-05

10.3969/j.issn.1673-629X.2016.08.034