基于四階微分全變差的圖像去噪模型

王 璐

(昆明理工大學 理學院，云南 昆明 650500)

基于四階微分全變差的圖像去噪模型

王 璐

(昆明理工大學 理學院，云南 昆明 650500)

針對現有全變差(TV)方法效果不太理想，在去除噪聲的時候不能較好地保護圖像的邊緣信息，而且恢復圖像易出現“階梯效應”和“塊效應”的問題，文中提出了一種基于四階微分全變差的圖像去噪模型。首先論述了傳統全變差模型去噪方法及其高階微分方程去噪方法各自的優缺點；然后將帶有邊緣指標的全變差模型與四階微分理論相結合，得到了一個新的帶有邊緣指標的自適應全變差去噪模型，并引入差分方程去定義模型中的變量。實驗結果表明，該模型能較好地抑制噪聲、保留邊緣特征和衰減圖像的“階梯效應”，并能較好地避免圖像的“塊效應”。

圖像去噪；全變差；四階微分；邊緣保真；塊狀效應

0 引 言

在各類圖像系統中，由于圖像的傳送和轉換，如成像、復制、掃描、傳輸、顯示等，總要造成圖像的降質，最典型的表現為圖像失真，有噪聲等。去噪成為圖像復原的經典話題，然而在去噪的過程中不可避免地會導致圖像邊緣的模糊，而圖像的重要信息往往存在于高頻(邊緣,細節)區，傳統的濾波去噪很難有效地處理這類問題。

因此，尋找既能有效去除噪聲又能保持圖像邊緣特征的方法成為研究的重點[1]。

1 總變分模型

針對噪聲圖像，u0表示退化圖像，u表示原圖像，假定退化模型為：

u0=Ru+n

(1)

其中：u0表示退化圖像；u表示原圖像；n表示一個10倍的隨機干擾信號的加性噪聲；R表示確定性退化的線性算子，通常是卷積算子，這里R=I。

該去噪問題是一個典型的病態問題。數學上解決病態問題的一個常用方法是正則化方法，即加入一個正則項，使其呈良態。

1992年，Rudin等[2]從圖像復原的角度出發，對模型提出了基于能量極小化和變分(TotalVariation，TV)法的偏微分方程算法。該算法運用偏微分方程的各向異性擴散方程對圖像進行去噪。與傳統濾波去噪不同，各向異性擴散方程的優點[3]在于它的各向異性，即在不同的方向和區域，對于圖像的平滑程度也不同，它與圖像的局部結構有關。在灰度變化較大的區域或方向上，擴散作用較小；在灰度變化較小或孤立噪聲區域，采用較強的平滑處理，以達到抑制噪聲的目的。所以，各向異性擴散方法在圖像邊緣檢測、抑噪與邊緣保留、分割等方面都得到了廣泛應用。

然而，傳統的TV模型有三大缺點：計算的復雜度高、邊緣信息的不穩定性和恢復圖像出現的“階梯效應”。為了能夠更好地保留邊緣信息，Gilboa等在2003年提出了一種新的模型。該模型在傳統TV模型的基礎上，把傳統正則參數變形為自適應的正則參數，使得保真項隨著像素值的變化而發生相應的變化[4]。為了降低恢復圖像的“階梯效應”，Blomgren等提出了一種在遠離邊緣的區域可使ROF模型更凸的模型，即給梯度正則項添加了和梯度大小有關的指數項，使得模型在恢復圖像的過程中滿足圖像的線性[5]。自適應正則項和保真項的提出為圖像去噪又開辟了一條新的途徑，在模型[6]中同時包含了自適應的正則項和保真項：

EATV=∫Ω(|

其中，p(D):R+→[1,2]，λ(D)∈[0,k]。

在邊緣區，正則項近似于TV范數用來保護邊緣區；在平滑區，正則項近似于L2范數，保真項的權重較小，有利于圖像去噪。

為了衰減“階梯效應”，提高邊緣的穩定性，一些文獻中用高階差分算子代替TV范數。與一階梯度正則項不同，高階微分能恢復圖像中潛在的分段常量區域，有效地恢復圖像的平滑性并有效降低圖像的“階梯效應”[7-14]。在這種情況下，提出了合并二階差分和TV范數作為正則項模型[7,10-11]：

E=∫Ω(|Δf(x)|+λ(u-u0)2)dxdy

(3)

其中，Δf(x)=fxx+fyy，分別為f對x的二階導數和對y的二階導數。

也可以直接使用二階正則項構造圖像去噪模型[9,13]。然而，利用二階導數對圖像去噪后，圖像會出現“塊效應”，如果圖像強度函數是二維時，圖像的各向異性擴散是導致恢復圖像出現“塊效應”的重要因素[12]。這樣，在視覺上，恢復圖像就會呈現不好的效果。另外，計算機識別圖像時，很有可能在視覺上出現系統性的錯誤，實際上是原始圖像中平滑區不同塊的分界，而被誤認為是圖像的邊緣區。這樣對于這些分段平面圖像噪聲的移除和邊緣的保護仍有缺陷。然而四階差分項在避免圖像“塊狀效應”的同時也能夠很好地實現噪聲消除和邊緣保護。

綜上所述，對于圖像去噪，這些高階正則項模型在去噪的過程中，在保護邊緣和降低圖像的“階梯效應”方面優于單純的TV正則項模型。

文中模型利用高階微分對于圖像去噪的優勢，采用四階微分方程做正則項來對圖像進行去噪，并在模型中引入自適應的正則項和保真項。數值實驗表明，該模型在移除噪聲和保護邊緣的同時，能有效地避免圖像的塊狀效應，衰減恢復圖像出現的“階梯效應”。

2 高階全變差去噪模型

全變差模型為：

E(u)=?Ωf(|pu|)dxdy

(4)

則全變差模型可寫為：

(5)

其Euler方程為：

式(5)化為梯度穩定形式即為：

在計算過程中，當t達到一定的值時，恢復圖像在去除噪聲和邊緣的保護上達到一個最優值。

3 改進的四階去噪模型

3.1 邊緣指標

邊緣指標是根據梯度模的大小來區分邊緣區域和平滑區域的，它的缺點是不能考慮到圖像中不連續的情況，因而不能很好地對邊緣區進行恢復。而與一階導數相比，二階導數不僅可以考慮不連續情況，而且對邊緣信息更敏感，所以使用二階導數可有效地區分出圖像的邊緣區域和平滑區域。下面引入一個體現邊緣指標的參數，即差分曲率的定義：

D=||uηη|-|uξξ||

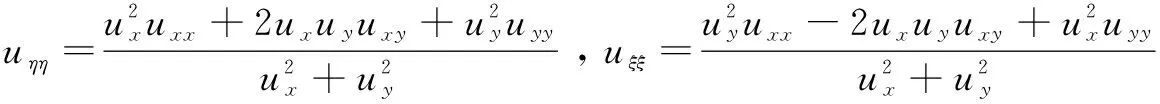
因為邊緣區域梯度模值大，而平滑區域梯度模值小，所以上式通過二階導數之間的關系，對邊緣指標進行分析(見表1)：

表1 差分曲率特征分析

這樣就可以有效地區分圖像的邊緣區域、平坦區域和噪聲區域，從而更好地達到保護邊緣的目的。

3.2 四階全變差去噪模型及其模型求解

利用差分曲率對圖像去噪的優勢，定義兩個自適應參數：

則含有自適應差分曲率的模型為：

(6)

則模型(6)對應的Euler方程為：

(7)

在對Euler方程求解時，可把方程轉化為偏微分穩定形式進行求解，方程(7)的穩定形式為:

(8)

其中，h表示差分方程的步長。

邊界條件為：

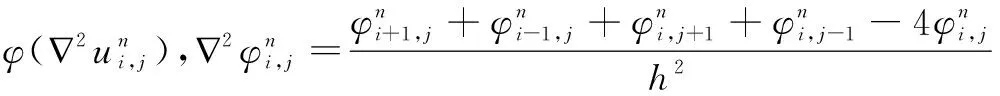
4 數值實驗

文中仿真平臺軟件環境為Matlab7.14；硬件環境為英特爾i3-2350M@2.30GHz，內存2GB。

為驗證去噪模型及其算法的有效性，將文中方法與ROF去噪法、一階自適應TV(ATV1)去噪法、二階自適應TV(ATV2)去噪法進行比較。以峰值性噪比和結構相似度作為衡量指標。選取Lena圖像和Flower圖像，噪聲類型為加性10倍的隨機干擾噪聲。

文中模型參數為：k=2，迭代步長Δt=1×0.02，迭代次數n=50，圖像迭代的精度tol=10-4。

圖1和圖2分別是Lena圖像和Flower圖像的去噪結果；表2和表3為算法對比結果。

圖1 Lena圖像的4種去噪結果

表2 算法比較結果(Lena圖像)

圖2 Flower圖像的4種去噪結果

算法PSNRSSIM噪聲圖17.72550.3387TV21.94170.5518ATV123.16270.7318ATV223.21160.7338文中模型23.36000.7360

由恢復圖像特征及其峰值信噪比、結構相似度可知，運用TV模型去噪時，圖像的細節部分被破壞，而且恢復圖像存在“階梯效應”；運用線性ATV模型去噪時，圖像邊緣信息保護比較好，由于圖像像素值存在分段常量，使得恢復圖像仍存在“階梯效應”和“塊效應”；而運用文中模型不僅可以有效地去除噪聲，保護圖像邊緣，更減弱了恢復圖像非線性的結構模式，并避免了圖像的“塊效應”，證明該模型是有效的。

5 結束語

文中提出了一個四階差分自適應正則序列去解決圖像加噪聲后的非線性問題，并結合邊緣指標區分出了圖像的平滑區、邊緣區和噪聲區。實驗結果表明，與其他模型相比，此模型和算法在圖像去噪過程中能獲得更好的恢復結果。

[1] 岡薩雷斯.數字圖像處理[M].阮秋琦，譯．第2版.北京：電子工業出版社，2003.

[2]RudinLI,OsherS,FatemiE.Nonlineartotalvariationbasednoiseremovalalgorithms[J].PhysicaD,1992,60:259-268.

[3]ZhaoD,HeCJ,ChenQ.Anisotropicdiffusionmodelcombinedwithlocalentropy[J].PatternRecognitionandArtificialIntelligence,2012,25(4):642-647.

[4]GilboaG,ZeeviYY,SochenN.Texturepreservingvariationaldenoisingusinganadaptivefidelityterm[C]//ProceedingsoftheVLSM.Nice,France:[s.n.],2003:137-144.

[5]BlomgrenP,ChanTF,MuletP.Extensionstototalvariationdenoising[J].ProceedingsofSPIE,1997,3162:367-375.

[6]ChenQ,MontesinosP,SunQS,etal.Adaptivetotalvariationdenoisingbasedondifferencecurvature[J].ImageandVisionComputing,2010,28(3):298-306.

[7]LvXG,SongYZ,WangSX,etal.Imagerestorationwithahigh-ordertotalvariationminimizationmethod[J].AppliedMathematicalModelling,2013,37(16-17):8210-8224.

[8]LysakerM,TaiXC.Iterativeimagerestorationcombiningtotalvariationminimizationandasecond-orderfunctional[J].InternationalJournalofComputerVision,2006,66(1):5-18.

[9]YuanJ,Schn?rrC,SteidlG.Total-variationbasedpiecewiseaffineregularization[C]//ProcofSSVM.Berlin:Springer-Verlag,2009:552-564.

[10]ChambolleA,LionsPL.Imagerecoveryviatotalvariationminimizationandrelatedproblems[J].NumerischeMathematik,1997,76(2):167-188.

[11]ChanTF,EsedogluS,ParkFE.Imagedecompositioncombiningstaircasereductionandtextureextraction[J].J.Vis.Commun.ImageRepresent.,2007,18(6):464-486.

[12]YouYL,KavehM.Fourth-orderpartialdifferentialequationsfornoiseremoval[J].IEEETransactionsonImageProcessing,2000,9(10):1723-1730.

[13]LefkimmiatisS,BourquardA,UnserM.Hessian-basedregularizationfor3-Dmicroscopyimagerestoration[C]//ProceedingsofIEEEinternationalsymposiumonbiomedicalimaging.[s.l.]:IEEE,2012:1731-1734.

[14]JideshP,GeorgeS.Fourth-orderGausscurvaturedrivendiffusionforimagedenoising[J].InternationalJournalofComputer&ElectricalEngineering,2012,4(3):350-354.

[15] 王大凱,侯榆青,彭進業.圖像處理的偏微分方程方法[M].北京:科學出版社,2008.

[16] 王旭東，馮象初，張選德.去除乘性噪聲的迭代重加權二階正則模型[J].西安電子科技大學學報，2014，41(2)：130-136.

Image De-noising Model Based on Total Variation of Fourth-order Differential

WANG Lu

(Faculty of Science,Kunming University of Science and Technology,Kunming 650500,China)

The effect of the existing Total Variation (TV) method for image denoising is not ideal while removing noise,it is not well protection of the edge information of image and easy to appear the "staircase effect" and "blocky effect" when recovering the image.Aiming at this problem,a new method of image denoising based on TV of fourth-order differential is proposed in this paper.First,the advantages and disadvantages of the traditional image denoising methods of TV and higher order differential equations are discussed respectively.Then,combined the denoising model of TV with fourth-order differential theory,a new adaptive ATV model with the edge indicator is obtained,and a rational differential mask in eight directions is drawn.The experimental results show that this method can reduce the noise well,and preserve edge features better,and reduce the influence of the "staircase effect",avoiding the "blocky effect" of the image.

image denoising;total variation;fourth-order differential;edge fidelity；blocky effect

2015-06-20

2015-09-22

時間：2016-02-18

國家自然科學基金資助項目(11461037)；昆明理工大學人才基金(2008-72)；昆明理工大學研究生核心課程項目

王 璐(1990-)，女，碩士研究生，研究方向為數字圖像處理。

http://www.cnki.net/kcms/detail/61.1450.TP.20160218.1638.088.html

TP391.41

A

1673-629X(2016)03-0085-04

10.3969/j.issn.1673-629X.2016.03.020