動態步長的RRT路徑規劃算法
王道威,朱明富,劉 慧
(華中科技大學 自動化學院,湖北 武漢 430074)
動態步長的RRT路徑規劃算法
王道威,朱明富,劉 慧
(華中科技大學 自動化學院,湖北 武漢 430074)
傳統的快速擴展隨機樹(RRT)算法雖然有很多優良特性,但是由于擴展點的隨機選取,規劃出來的路徑具有很大的隨機性。文中在對RRT算法改進的基礎上,提出了一種動態步長的RRT路徑規劃算法。其中步長為RRT生長的最小單位長度。動態步長的RRT算法是在對傳統RRT算法的基礎上,添加了動態步長的特性,改善了快速擴展隨機樹的不確定性,提高了避障能力,使得算法確定性和高避障能力兼備。仿真實驗結果表明,該算法在路徑規劃中具有路徑確定、速度快和高避障能力的特點。
快速擴展隨機樹;動態步長;路徑確定性;高避障能力
0 引 言
隨著無人機、無人汽車等無人智能設備的不斷應用和發展,RRT路徑規劃算法[1-3]越來越多地被應用。RRT算法是一種隨機搜索算法,它能在保證系統實時性的前提下,尋找到問題的較優解。但是RRT算法具有隨機性[4],規劃出來的路徑偏離目標點,與理想路徑相比有較大差異。
文中在經典RRT算法的基礎上引入目標引力函數,讓隨機樹朝著目標點方向生長,使得規劃出來的路徑更加接近理想路徑。但是這種添加了目標引力函數的RRT算法雖然降低了路徑的隨機性,但同時也降低了算法的避障能力,起始點和目標點障礙物比較多的情況下不能規劃出路徑。文中在RRT算法的基礎上引入了動態步長的概念。步長即為RRT生長的最小單位長度。在RRT算法擴展新節點時,當遇到障礙物時自動減小目標點方向的步長,沒遇到障礙物時再恢復原步長。改進后的RRT路徑規劃算法兼具路徑確定性和高避障能力的優點。
1 RRT算法
快速隨機擴展樹(RRT)算法由Steven M. LaValle于1998年在文獻[5]中首先提出。RRT算法是從空間中一個起始節點出發,通過隨機采樣,不斷增加新節點,生成一個隨機擴展樹。當增加的新節點中有目標節點時,起始節點到目標節點就會至少有一條通路,稱為路徑。RRT算法已應用于飛行器運動規劃[6]和移動機器人路徑規劃中[7]。
1.1 經典RRT算法
RRT算法的作用是在度量空間X中,選擇一條從初始狀態點xinit到目標狀態點xgoal或者到目標狀態點區域xgoal∈X的路徑。通常選擇距離空間C作為度量空間,即X=C。在度量空間中路徑無法通過的區域稱為障礙區域,記為xobs∈X。障礙區域在度量空間中的補集稱為自由區域,記為xfree∈X。令xrand為每次擴展RRT時在自由區域中隨機選取的點,xrand∈xfree。令xnear為每次擴展RRT時在當前RRT中與xrand距離最近的點。xnew為每次新增加的擴展點。給定一個初始狀態xinit,一個隨機擴展樹T,生成K個頂點的方法如下:
GENERATE_RRT(xinit,K,△t)
T.init(xinit);
Fork=1toKdo
xrand←RANDOM_STATE();
xnear←NEAREST_STATE(xrand,T);
u←SELECT_INPUT(xrand,xnear);
xnew←NEW_STATE(xnear,u,△t);
T.add_vertex(xnew);
T.add_edge(xnear,xnew,u);
ReturnT
其中,RANDOM_STATE()在自由空間中隨機選取一點xrand,NEAREST_STATE()在當前RRT中選擇與xrand距離最近的點xnear,SELECT_INPUT()結合xrand和xnear得到輸入u,NEW_STATE()得到新節xnew。
1.2 引入目標引力思想的RRT算法
在文獻[1]中介紹了一種引入目標引力思想的RRT算法,能有效減少RRT算法的隨機性,讓路徑朝著目標方向擴展。
在文獻[2]中介紹了一種目標偏好RRT算法,該算法大部分擴展過程使用隨機點,以一定小概率選取目標點取代隨機點,將隨機樹向目標區域擴展。
文獻[3]中對目標偏好RRT算法做了進一步改進,使它應用于非完整微分約束中。
經典的RRT算法隨機性比較明顯,規劃出來的路徑非常曲折,不適合實際使用中的路徑規劃。經典RRT算法新節點位置的計算公式如式(1)所示。
(1)
其中,ρ為RRT生長的最小單位長度,稱為步長。
加入目標引力思想的RRT算法新節點位置的計算公式如式(2)所示。
(2)
其中:ρ1為隨機點方向的步長;ρ2為目標點方向的步長。
2 動態步長的RRT算法
路徑規劃是按照某一性能指標搜索一條從起始狀態到目標狀態的最優或近似最優的無碰路徑[8]。動態步長的RRT算法能夠規劃出比較理想的無碰路徑。
2.1 步長對RRT算法的影響
首先考慮步長在經典RRT路徑規劃算法中的作用。經典隨機擴展樹生成算法擴展一個新節點的過程為:首先在度量空間中隨機選取一點xrand,然后在當前擴展樹中(可能為空)找到與xrand距離最近的點xnear,在xnear到xrand的方向上擴展一個步長的距離得到新節點xnew加入擴展樹中。
加入目標引力思想后的RRT算法能有效解決路徑隨機性強的問題。引入目標引力思想后的RRT算法與經典RRT算法相比添加了xgoal方向的分量。加入目標引力思想后,步長的選擇對新節點的位置會有影響。此時新節點不再在xnear到xrand的連線上了。當ρ2>ρ1時,新節點偏向于xgoal,由于xgoal的位置通常是固定的,擴展樹朝著xgoal方向擴展。當ρ2<ρ1時,新節點偏向于xrand,由于xrand的位置是隨機選取的,此時擴展樹的擴展方向接近RRT經典算法。
引入目標引力思想后的隨機擴展樹朝著目標點方向發展,規劃出來的路徑更加接近理想路徑。ρ2相對于ρ1取的越大,擴展樹越朝著xgoal方向擴展,規劃出來的路徑越接近理想路徑。
以上所討論的都在無障礙空間中規劃路徑,在實際的路徑規劃應用中,起始點和目標點之間都或多或少存在很多障礙,很難找到一個有效的路徑規劃方法來應對各種復雜環境[9]。規劃出的路徑需要避開所有障礙到達目標點。經典RRT算法新節點的添加都是隨機方向的,能夠有效地避開障礙。引入目標引力的RRT算法常常為了能夠使規劃出的路徑接近理想路徑,目標點方向的步長要較大于隨機點方向的步長。此時如果起始點和目標點障礙物較多,那么擴展樹無法繞開障礙物到達目標點。
可以得出結論:路徑理想和避障能力是相互矛盾的。為了解決這對矛盾,在目標引力RRT算法基礎上添加了動態步長的概念。當沒有遇到障礙物時取ρ2>ρ1,使擴展樹盡可能朝著目標點方向擴展。當遇到障礙物時取ρ2<ρ1,使擴展樹朝著隨機點方向擴展,因為隨機點的隨機性,新節點也具有隨機性,從而可以高效地避開障礙物。
2.2 動態步長RRT算法的優點
經典RRT算法的隨機性很強,規劃出來的路徑與理想路徑相差很大,但由于擴展節點的隨機性,經典RRT算法具有很強的避障能力。
為了規劃出更加理想的路徑,在經典RRT算法中引入目標引力思想,讓新節點朝著目標節點的方向擴展。但是這種算法的避障能力很弱,當起始點和目標點間有很多障礙的時候不能規劃出路徑。
動態步長RRT算法具有以上兩種算法的優點,不僅能朝著目標節點擴展新節點,而且具有和經典RRT算法一樣的避障能力。動態步長RRT算法在路徑規劃中更加實用。和經典RRT算法一樣,該算法具有高效的搜索特性,使其適合解決高維空間多自由度的復雜約束下的運動規劃問題,能直接應用到非完整性約束或非完整性動力學約束規劃中[10]。
動態步長RRT算法時間復雜度低。在文獻[11-13]中介紹的滾動規劃算法,每次在一個窗口中規劃出最優路徑,時間復雜度很高。動態步長RRT算法在擴展每一個新節點時,只需計算一個式(2)的值。很多類似文獻[4]中提出的RRT改進算法,在擴展一個新節點時計算若干個隨機點的估價函數,選取估價函數值最小的作為新節點。這些做法使算法時間復雜度成倍增加。因為RRT擴展樹一般都具有非常多的節點,所以保持算法的較低的時間復雜度非常重要。
3 仿真實驗結果分析
實驗環境:Windows Embedded 8.1, Intel? CoreTMi5-3317U CPU @ 1.70 GHz, 內存8 G。
編譯工具:Visual Studio 2013。
圖1~5中左下角為起始節點,右上角為目標節點。圖中空心圓環為障礙物,距障礙物環心40個單位長度內的區域為障礙區域。圖中黑色粗線和黑色細線共同構成隨機擴展樹,黑色粗線連接起始點和目標點,被選為規劃出的路徑。
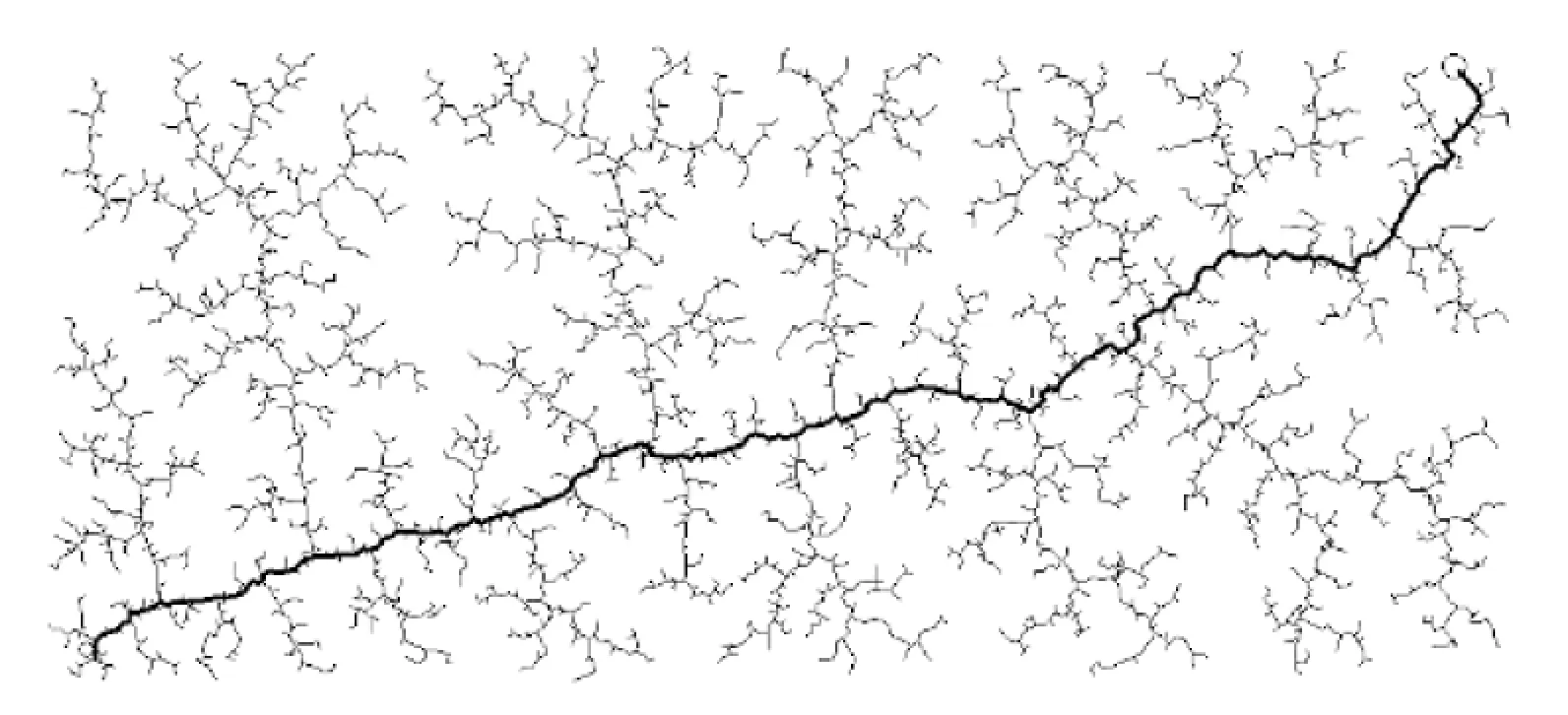
圖1 經典RRT算法(無障礙)

圖2 經典RRT算法(有障礙)
在無障礙的情況下,如圖1、3、4所示,都能規劃出路徑。由圖1可見,經典RRT算法的隨機性較強,路徑比較曲折。由圖3、4可見,目標引力RRT算法和動態步長RRT算法在無障礙情況下效果相同,規劃出的路徑比較接近理想路徑。

圖3 目標引力RRT算法(無障礙)

圖4 動態步長RRT(無障礙)

圖5 動態步長RRT(有障礙)
在有障礙的情況下,如圖2、5所示,目標引力RRT算法無法規劃出路徑,其他兩種算法都能規劃出路徑。由圖2可見,經典RRT算法能有效避開障礙物,但是隨機性較強。目標引力RRT算法在有障礙的情況下,由于起始點和目標點障礙物過多,隨機樹無法繞開障礙物到達目標節點,導致運行程序無響應。由圖5可見,動態步長RRT算法能有效避開障礙物,而且沒有經典RRT算法的隨機性。
4 結束語
經典RRT算法具有隨機搜索特性[14],因此具有很強的避障能力,而且生成的路徑不夠光滑,與理想路徑相差很遠。目標引力思想RRT算法犧牲了部分隨機性,規劃出的路徑更加光滑,但是減弱了避障能力,很多情況下無法規劃出路徑。動態步長的RRT算法不僅能夠規劃出接近理想路徑的路徑,而且具有很強的避障能力,算法時間復雜度低,能夠高效廣泛地應用在實際路徑規劃中。
[1] 郝利波,侯媛彬.基于一種改進RRT算法的足球機器人路徑規劃[J].西安科技大學學報,2011,31(1):81-85.
[2] Urmson C,Simmons R.Approaches for heuristically biasingRRTgrowth[C]//ProcofIROS.[s.l.]:[s.n.],2003:1178-1183.
[3] 徐 娜,陳 雄,孔慶生,等.非完整約束下的機器人運動規劃算法[J].機器人,2011,33(6):666-672.
[4] 王 濱,金明河,謝宗武,等.基于啟發式的快速擴展隨機樹路徑規劃算法[J].機械制造,2007,45(12):1-4.
[5]LaValleSM.Rapidly-exploringrandomtrees:anewtoolforpathplanning[R].Ames:IowaStateUniversity,1998.
[6]AminJN,BoskovicJD,MehraRK.Afastandefficientapproachtopathplanningforunmannedvehicles[C]//ProcofAIAAguidance,navigation,andcontrolconference.Keystone,Colorado:AIAA,2006:1-9.
[7] 樊曉平,李雙艷.帶滾動約束輪移式機器人動態規劃的研究[J].控制與決策,2005,20(7):786-788.
[8] 李 磊,葉 濤,譚 民,等.移動機器人技術研究現狀與未來[J].機器人,2002,24(5):475-480.
[9] 宋金澤,戴 斌,單恩忠,等.一種改進的RRT路徑規劃算法[J].電子學報,2010,38(2A):225-228.
[10]JouandeauN.Rapidly-exploringsortedrandomtree:aselfadaptiverandommotionplanningalgorithm[J].LectureNotesinElectricalEngineering,2009,24(5):63-73.
[11] 席裕庚.動態不確定環境下廣義控制問題的預測控制[J].控制理論與應用,2007,17(5):665-670.
[12] 趙春霞,唐振民,陸建峰,等.面向自主車輛的局部路徑規劃仿真系統[J].南京理工大學學報:自然科學版,2002,26(6):570-574.
[13] 張純剛,席裕庚.全局環境未知時基于滾動窗口的機器人路徑規劃[J].中國科學:E輯,2001,31(1):51-58.
[14] 康 亮,趙春霞,郭劍輝.未知環境下改進的基于RRT算法的移動機器人路徑規劃[J].模式識別與人工智能,2009,22(3):337-343.
Rapidly-exploring Random Tree Algorithm Based on Dynamic Step
WANG Dao-wei,ZHU Ming-fu,LIU Hui
(School of Automation,Huazhong University of Science and Technology,Wuhan 430074,China)
Although the traditional Rapidly-exploring Random Tree (RRT) algorithm has many good features,there is a lot of randomness in path planning of RRT because of the random selection of the vertex.Based on the improvement of RRT algorithm,a new RRT path planning algorithm of dynamic step size is proposed in this paper.The step size is the minimum unit length when RRT exploring.Based on traditional RRT,the dynamic step size is added,avoiding the uncertainty,and the obstacle avoidance capability is improved,thus the path planning of RRT algorithm has both obstacle avoidance ability and high certainty.The results of simulation experiments show that the algorithm has the features of avoiding the uncertainty,fast speed and obstacle avoidance in path planning.
RRT;dynamic step size;path planning certainty;obstacle avoidance
2015-06-30
2015-09-30
時間:2016-02-18
國家自然科學基金資助項目(61403154)
王道威(1989-),男,碩士研究生,研究方向為多智能體控制、圖像處理。
http://www.cnki.net/kcms/detail/61.1450.TP.20160218.1638.086.html
TP301.6
A
1673-629X(2016)03-0105-03
10.3969/j.issn.1673-629X.2016.03.025

