一類乘性有理樣條權函數神經網絡靈敏度分析

張代遠，王雷雷

(1.南京郵電大學 計算機學院，江蘇 南京 210003;2.江蘇省無線傳感網高技術研究重點實驗室，江蘇 南京 210003;3.南京郵電大學 計算機技術研究所，江蘇 南京 210003)

一類乘性有理樣條權函數神經網絡靈敏度分析

張代遠1,2,3，王雷雷1

(1.南京郵電大學 計算機學院，江蘇 南京 210003;2.江蘇省無線傳感網高技術研究重點實驗室，江蘇 南京 210003;3.南京郵電大學 計算機技術研究所，江蘇 南京 210003)

樣條權函數神經網絡是一種新型的神經網絡，它克服了傳統神經網絡收斂速度慢、初值敏感、局部極小的問題。因其能精確學習給定的樣本，并且結構簡單、訓練速度快，因此被廣泛關注。結合分子三次、分母一次的有理樣條函數和樣條權函數神經網絡的優勢，研究了分子三次、分母一次乘性有理樣條權函數神經網絡，并對其靈敏度進行了理論分析和實驗仿真。通過理論分析和仿真可以看出，該神經網絡具有分子三次、分母一次的有理樣條和樣條權函數神經網絡的優越特性，在一定擾動范圍內，該樣條權函數神經網絡的靈敏度穩定，具有很強的抗干擾能力。

樣條權函數；樣條插值；神經網絡；靈敏度分析

0 引 言

隨著云計算、機器學習和大數據計算的蓬勃興起，人工神經網絡理論和方法得到了更加廣泛的關注和應用。但是傳統的BP算法往往存在局部極小、不收斂或者收斂速度慢、初值敏感等缺陷。這些缺陷極大限制了神經網絡在實際工程中的應用。許多學者對傳統的BP算法進行了多方面的改進，比如采用遺傳算法調整網絡參數[1]，優化初始權值或者其他參數[2]等。但是這些改進無法從根本上克服梯度下降類算法的缺點。文獻[3]提出了新的神經網絡(樣條權函數神經網絡)及其訓練算法，該算法能夠精確學習給定的樣本，克服了傳統算法(如BP算法等)存在的局部極小、收斂速度慢、初值敏感等缺點。由于樣條插值在曲線和平面設計中的重要作用，許多學者對其進行了大量研究[4-5]，發現分子三次、分母一次的有理樣條[6]能夠很好地逼近目標函數，而且通過選取適當參數可以使其獲得很好的形狀控制能力[7]。

當輸入樣本或者權值存在擾動時，樣條權函數神經網絡的輸出會發生變化。從理論上分析這些變化對于整個網絡系統產生的影響是很重要的。靈敏度作為神經網絡的一個重要指標，可以分析這些變化給系統帶來的影響，而且有不少學者對靈敏度或者神經網絡靈敏度做過分析[8-11]。文中結合分子三次、分母一次的有理樣條函數和樣條權函數神經網絡的優勢，研究分子三次、分母一次乘性有理樣條權函數神經網絡，利用文獻[10]中對靈敏度的定義，對其靈敏度進行了分析。該神經網絡具有分子三次、分母一次的有理樣條和樣條權函數神經網絡的優越特性，可以被廣泛應用到工程實踐中。

1 分子三次、分母一次乘性有理樣條權函數神經網絡

文獻[3]提出的樣條權函數神經網絡，只有兩層。為了簡單起見，這里引用多輸入單輸出的乘性樣條權函數神經網絡結構，如圖1所示。其中輸入樣本向量是m維，因此輸入端有m個節點，每個輸入端節點通過連接權前饋連接到所有乘法單元。對于多輸入多神經輸出網絡，可以得到類似的網絡結構[3]。

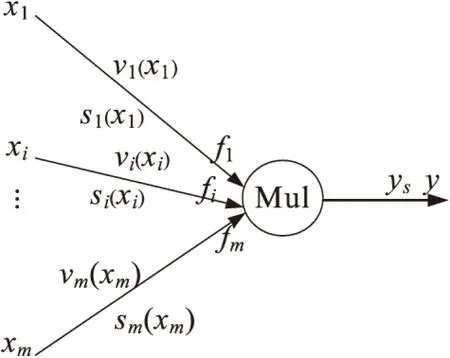
圖1 多輸入單輸出乘性樣條權函數神經網絡結構

從圖中可以看出，輸入向量x有m維，其中xi,i=1,2,…,m為m維輸入向量的第i個分量。假設有N+2個訓練樣本，則xi的向量表示為：

(1)

那么對應輸出節點的向量表示為：

(2)

(3)

乘積因子ρi表示每一個輸入端節點對相應輸出的貢獻大小，ρi越大說明輸入節點在網絡訓練中對輸出的影響越大。近似權函數si(xi)由輸入向量xi和輸出向量fi決定，所以對應的插值點為：

(4)

既然已經得到了插值點，那么就可以通過數學上的插值方法精確通過這些插值點(樣本點)，所以說權函數神經網絡是精確學習算法，就是說經過訓練的網絡能夠精確“回想”起已經學過的樣本。

插值理論方法豐富多彩，考慮到實際樣本可能會在極點附近，或者一些應用中需要考慮形狀控制時，有理函數具有一定的優勢。因此文中采用分子三次、分母一次有理樣條函數作為權函數，這與文獻[3]所采用的插值多項式是不同的。

根據文獻[6-7]，對分子三次、分母一次有理樣條函數給出如下定義：

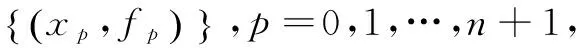
(5)

(6)

(7)

其中

(8)

(9)

Δp=(fp+1-fp)/hp,αp,βp>0，為形狀控制參數。

2 分子三次、分母一次乘性有理樣條權函數神經網絡靈敏度分析

2.1 靈敏度的統計學定義

對圖1所示的神經網絡，統計靈敏度定義[10]為：

(10)

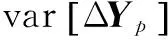
對于多個輸入樣本，假設第p個輸入樣本的靈敏度為Sp,p=0,1,…,N+1，通常，可以采用以下兩種方式來評價神經網絡的統計靈敏度。

采用所有樣本中的最大靈敏度：

(11)

采用所有樣本的平均靈敏度：

(12)

2.2 模型逼近誤差和逼近噪聲誤差分析

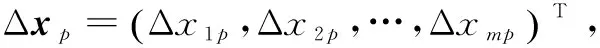
(13)

根據上述的神經網絡理論噪音誤差輸出值的運算方法，對網絡輸出值的理論噪音誤差進行具體分析。

先考慮輸出層第j個神經元理論噪音輸出誤差。同樣地，假設第p個不含噪聲的標準輸入樣本為

在這種輸入情況下，第j個神經元的理論輸出值為：

(14)

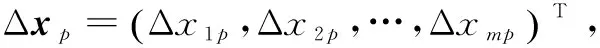
則第j個神經元的理論噪音輸出誤差為：

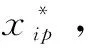
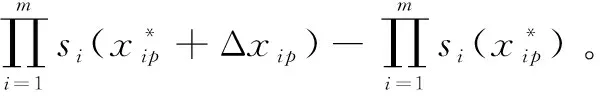
(17)

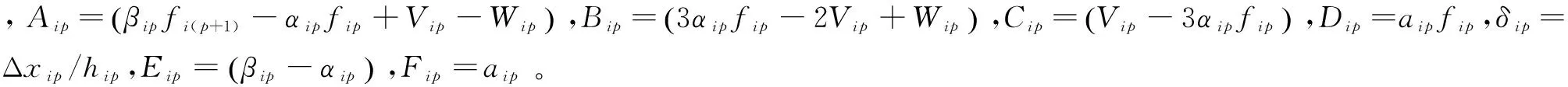
因為δip→0，所以

(18)

因此可得：

(19)

將Dip,Fip,δip代入式(19)可得：

(20)

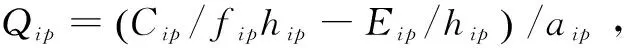
(21)

而對于多輸入多輸出乘性樣條權函數逼近噪聲誤差的表達式，可以由式(21)增加反映輸出節點序號的加下標j表示。

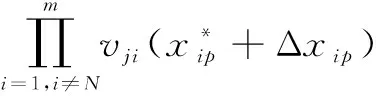
(22)

因此可得:

顯然，根據式(13)可知，多輸入多輸出的輸出層誤差可以表示成如下的矩陣形式：

(24)

此時可以將式(11)或式(12)中增加反映式(24)中行、列的下標即可。這樣可以得到多維輸出神經網絡靈敏度，因此根據式(10)、(11)、(12)、(24)就可以計算出分子三次、分母一次乘性有理樣條權函數神經網絡的統計靈敏度。

3 仿真實驗

下面進行數值仿真實驗，驗證分子三次、分母一次乘性有理樣條權函數的靈敏度穩定性。

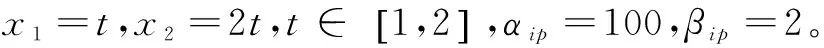
R=(Y*-Y)/Y

(25)

其中，Y*表示沒有擾動時的輸出；Y表示有擾動時的目標輸出。

靈敏度的實際仿真值采用數理統計[13]的方法求得，對不同組的擾動利用式(21)計算網絡輸出層誤差，然后再統計出擾動的標準差和網絡輸出層誤差的方差，按照式(10)計算靈敏度仿真值。平均相對誤差曲線和靈敏度曲線分別如圖2和圖3所示。

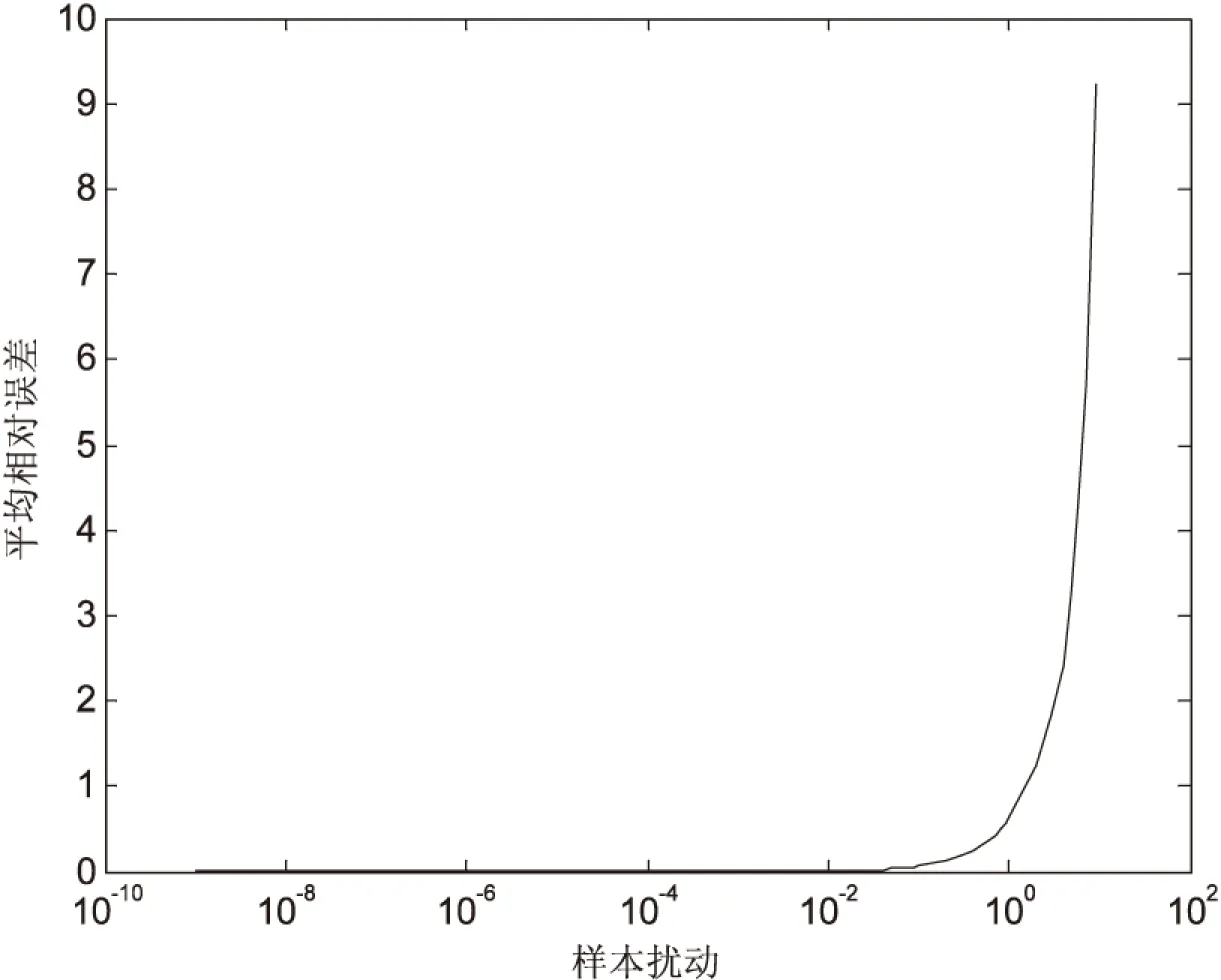
圖2 平均相對誤差曲線(學習曲線為x1=t,x2=2t)

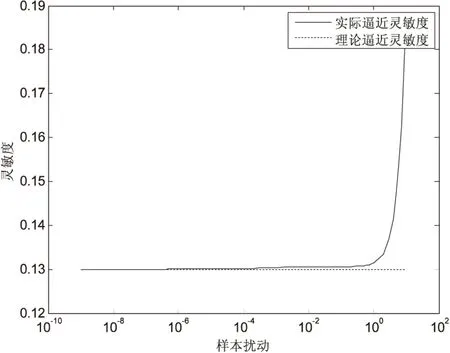
圖3 靈敏度曲線(學習曲線為x1=t,x2=2t)

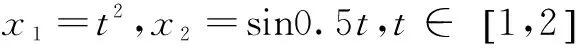
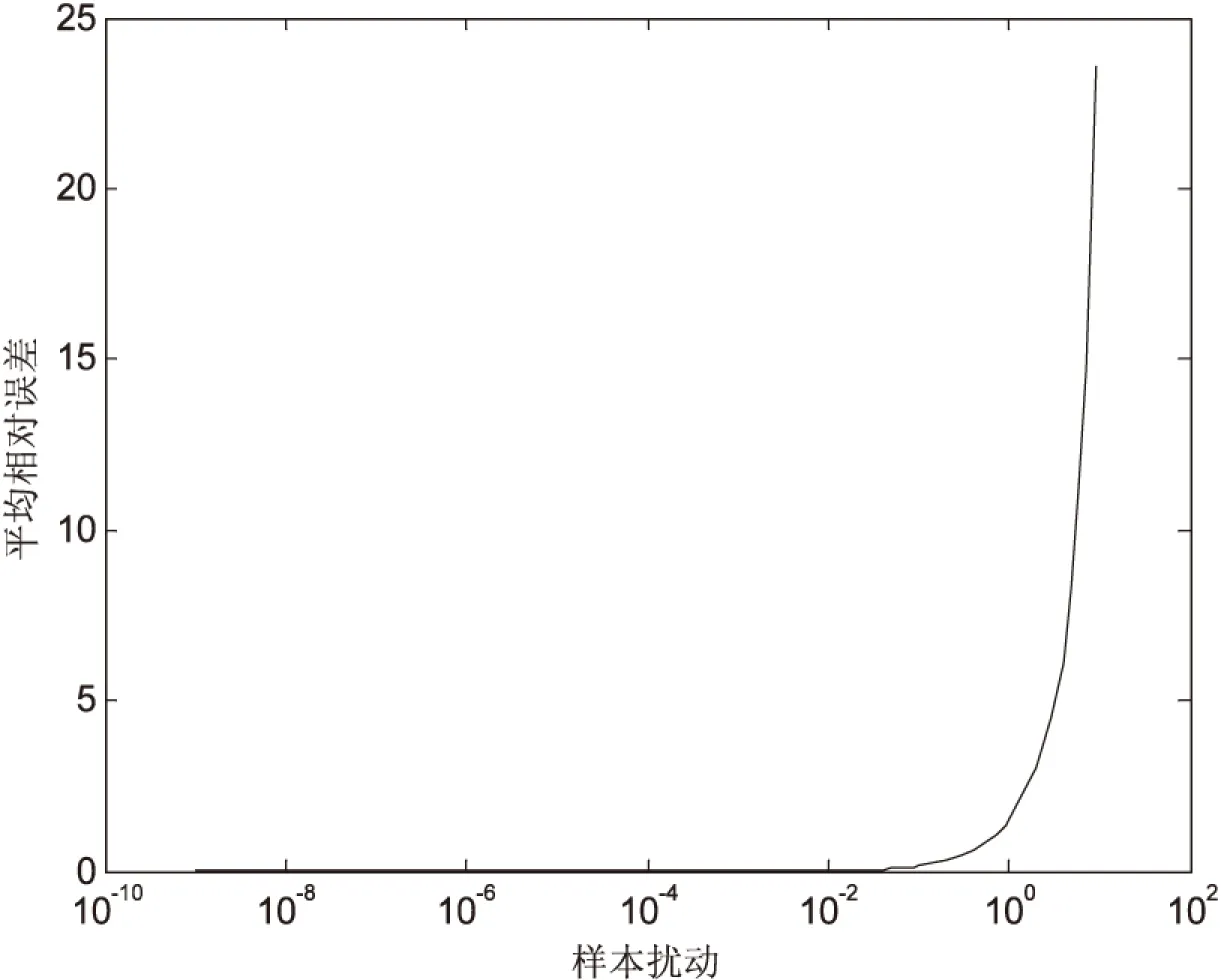
圖4 平均相對誤差曲線(學習曲線為x1=t2,x2=sin0.5t)

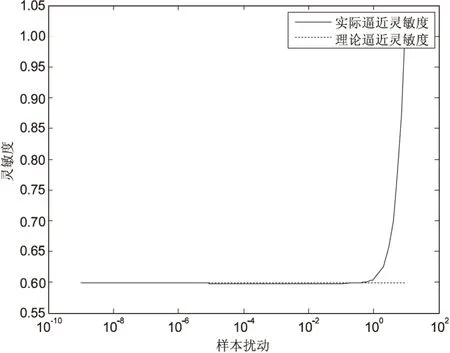
圖5 靈敏度曲線(學習曲線為x1=t2,x2=sin0.5t)

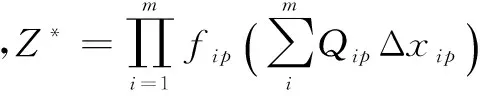
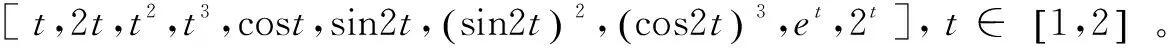
輸入維數對平均相對誤差的影響如表1所示。

表1 輸入維數對平均相對誤差的影響

從表1可以看出，當輸入維數m≤1 000時，平均相對誤差非常小，即Z*非常接近Z。而根據UCIrvineMachineLearningRepository的數據，92%的數據集輸入屬性個數小于1 000，因此式(21)具有實用性和代表性。

4 結束語

文中將樣條權函數神經網絡和分子三次、分母一次的有理樣條相結合，研究分子三次、分母一次乘性有理樣條權函數神經網絡靈敏度。通過理論分析和仿真實驗，表明當擾動在較寬的變化范圍內，靈敏度值非常穩定。在此擾動范圍內神經網絡的仿真輸出與目標樣本的理論輸出偏差很小，能與目標樣本較好匹配。說明當樣本擾動在一定范圍內時，分子三次、分母一次乘性有理樣條權函數神經網絡的網絡泛化能力[14]不會受到外界噪聲的影響，即具有較強的抗干擾能力，可以廣泛應用于工程實踐的各個領域。

[1]KhashmanA.Amodifiedbackpropagationlearningalgorithmwithaddedemotionalcoefficients[J].IEEETransactionsonNeuralNetworks,2008,19(11):1896-1909.

[2]WedgeD,IngramD,McLeanD,etal.Onglobal-localartificialneuralnetworksforfunctionapproximation[J].IEEETransactionsonNeuralNetworks,2006,17(4):942-952.

[3] 張代遠.神經網絡新理論與方法[M].北京:清華大學出版社,2006.

[4]SunQ,BaoF,DuanQ.Shape-preservingweightedrationalcubicinterpolation[J].JournalofComputationalInformationSystems,2012,8(18):7721-7728.

[5]BaoF,SunQ,DuanQ.Pointcontroloftheinterpolatingcurvewitharationalcubicspline[J].JournalofVisualCommunication&ImageRepresentation,2009,20(4):275-280.

[6]DuanQ,DjidjeliK,PriceWG,etal.Arationalcubicsplinebasedonfunctionvalues[J].Computers&Graphics,1998,22(4):479-486.

[7]DuanQ,DjidjeliK,PriceWG,etal.Weightedrationalcubicsplineinterpolationanditsapplication[J].JournalofComputational&AppliedMathematics,2000,117(2):121-135.

[8] 張代遠.零代價函數條件下的前饋神經網絡統計靈敏度分析[J].模式識別與人工智能,2004,17(4):510-515.

[9]ZhangD.Anewalgorithmoftrainingneuralnetworksbyorthogonalweightfunctionsandsensitivityanalysis[C]//Procof2012IEEE5thinternationalconferenceonadvancedcomputationalintelligence.[s.l.]:IEEE,2012:324-327.

[10]ChoiJY,ChoiCH.Sensitivityanalysisofmultilayerperceptronwithdifferentiableactivationfunctions[J].IEEETransactionsonNeuralNetworks,1992,3(1):101-107.

[11]LiCG,LiHF,ZhangYF,etal.Sensitivityanalysisofmultilayerperceptronbasedonelasticfunction[C]//Procofinternationalconferenceonmachinelearningandcybernetics.[s.l.]:IEEE,2010:1490-1493.

[12]ZhangDY,WangLL.Erroranalysisofneuralnetworkwithmultiplyneuronsusingrationalsplineweightfunctions[J].AppliedMechanicsandMaterials,2015,713-715:1716-1720.

[13]NgWWY,YeungDS,RanQ,etal.Statisticaloutputsensitivitytoinputandweightperturbationsofradialbasisfunctionneuralnetworks[C]//ProcofIEEEinternationalconferenceonsystems,manandcybernetics.[s.l.]:IEEE,2002:503-508.

[14]ZhangDY.Analysisofgeneralizationforanewkindofneuralnetwork[J].AdvancedMaterialsResearch,2013,760-762:2023-2027.

Sensitivity Analysis of Neural Network with Rational Spline Weight Functions Using Multiplicative Neurons

ZHANG Dai-yuan1,2,3,WANG Lei-lei1

(1.College of Computer,Nanjing University of Posts and Telecommunications,Nanjing 210003,China；2.Key Laboratory of Jiangsu High Technology Research for Wireless Sensor Networks,Nanjing 210003,China;3.Institute of Computer Technology,Nanjing University of Posts and Telecommunications,Nanjing 210003,China)

The neural network with spline weight function is a new kind of neural network,which overcomes many problems such as slow convergence speed,sensitive to initial value and local minima.It is widely concerned because of its accurate learning approach to given patterns,simple network topology,fast training speed and so on.Based on the advantage of neural network with spline weight function,the sensitivity of neural network with cubic numerator and linear denominator of rational spline weight functions using multiplicative neurons is discussed,and the accuracy of analytical results is verified by simulation.Both the theoretical analysis and simulation results show that when the disturbance is in a certain range,the sensitivity of this kind of spline weight function neural network is very stable,and is featured with strong noise resistance.

spline weight function;spline interpolation;neural network;sensitivity analysis

2016-01-05

2016-05-12

時間：2016-09-19

江蘇高校優勢學科建設工程資助項目(yx002001)

張代遠(1957-)，男，教授，博士，碩士生導師，研究方向為人工智能、計算機體系結構、計算機應用等；王雷雷(1991-)，男，碩士研究生，研究方向為智能計算技術與應用。

http://www.cnki.net/kcms/detail/61.1450.TP.20160919.0841.038.html

TP301

A

1673-629X(2016)10-0050-05

10.3969/j.issn.1673-629X.2016.10.011